Решение астрономических задач

1. Решение астрономических задач

полное решение всех
типов задач по астрономии

2.

3.

Абсолютная звёздная величина (М)
Звёздная величина, которую имела бы звезда, если
бы находилась на расстоянии 10 Пк называется
абсолютной звёздной величиной (М)
M = m + 5 -5lg r
M = +4,8
m

4.

Расстояние до звёзд
Световой год – расстояние,
которое свет проходит за
один земной год
1 св.год=63240а.е.
Парсек(Пк) – расстояние, с
которого большая полуось
Земной орбиты видна под углом
1 сек.
D
СВ . Г
r
Пк
3,26
P
//
1
//
1 Пк = 3,26 св.г = 206265 а.е. = 30000000000000 км
Способ параллакса – для звёзд не далее 100 Пк
или 300 св. лет

5.

Метод параллакса
М (звезда)
Базис – большая полуось орбиты Земли
Годичный параллакс – угол под
которым со звезды видна большая
полуось Земной орбиты,
развёрнутая перпендикулярно
направлению на звезду
r
206265//
//
π
r
a.e.
Солнце
а
Земля

6.

Пространственная скорость звёзд υ
υ τ -тангенциальная скорость
υ r -лучевая скорость
υ=
υ2τ
υ
+
υ2r
φ
υτ
υr
S ( звезда)
( наблюдатель)
М

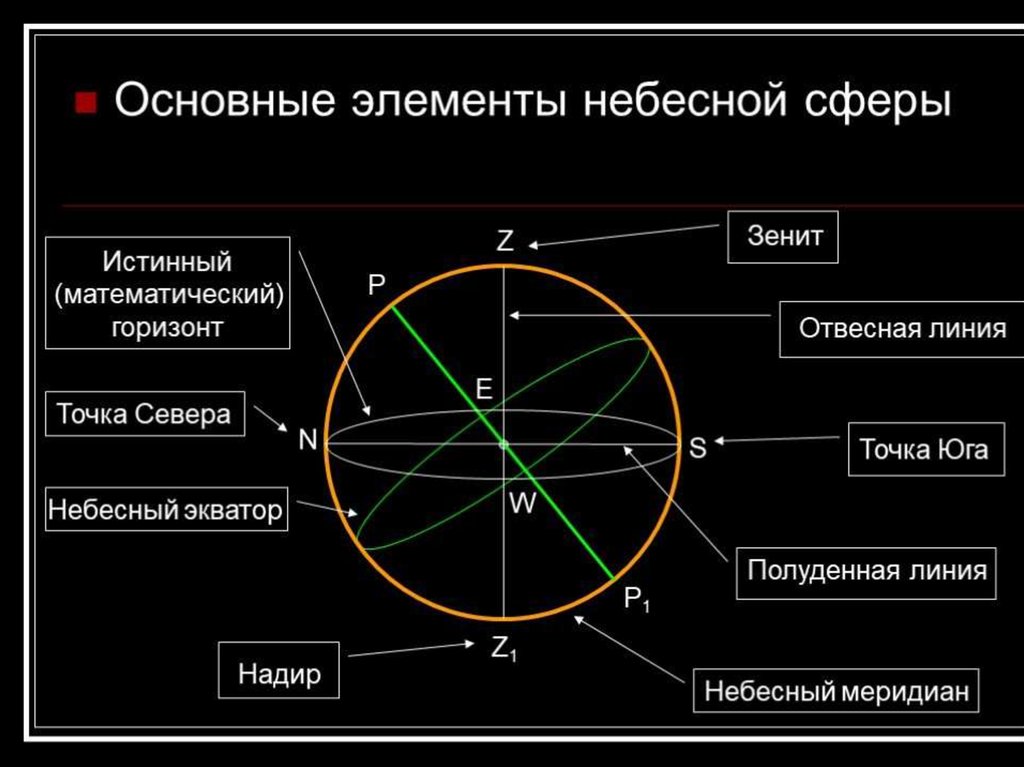
7.

8.

1. В местный полдень путешественник отметил 14 ч 13 мин по гринвичскому
времени. Определите географическую долготу места наблюдения.
Дано:
Т =12 ч
Т0=14ч 13 мин
–?
Решение:
Т λ = Т0 + λ
λ = Т λ -Т0
λ=12 ч -14 ч 13 мин = 2 ч 13 мин з.д.
Ответ: 2 ч 13 мин з.д.

9. Задачи

1. Каков синодический период Марса, если его звездный период равен 1,88
земного года?
Дано:
Т=1,88 года
Т0=1год
S–?
Решение:
1 1 1
S T0 T
T0T
S
T T0
S
1год 1,88года
2,136года
1,88года 1год
Ответ: 2,136 года

10. Задачи

1. Определите афелийное расстояние астероида Минск, если большая полуось его
орбиты равна 2,88 а.е., а эксцентриситет составляет 0,24.
Дано:
а=2,88 а.е.
е =0,24
Q a 1 e
Q–?
Q 2,88 1 0,24 3,57а.е.
Решение:
Ответ: 3,57 а.е.

11. Задачи

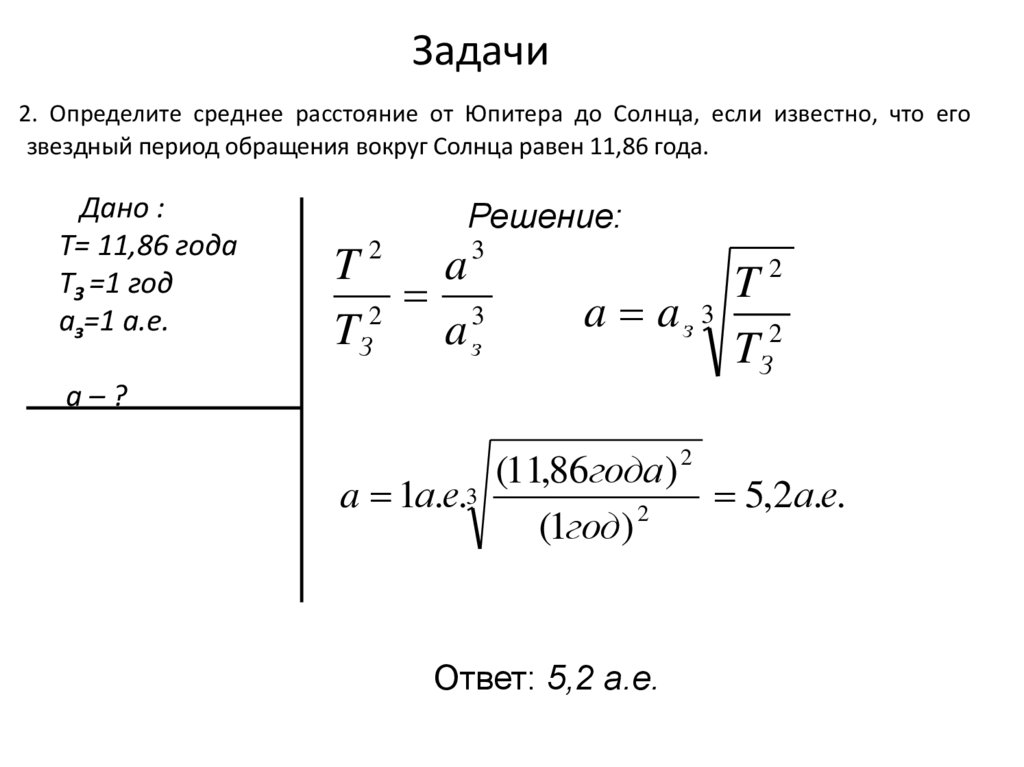
2. Определите среднее расстояние от Юпитера до Солнца,
если
2
3 известно, что его
звездный период обращения вокруг Солнца равен 11,86 года.
2
3
Дано :
з
Решение:З
Т= 11,86 года
2
3
2
T
a
T
a
ТЗ =1 год
аз=1 а.е.
а–?
T
a
3
2
TЗ
aз
a aз 3
2
T
TЗ2
T
a aз 3 2
2
(
11
,
86
года
)
a 1а.е.3 TЗ
5,2а.е.
2
(1год)
Ответ: 5,2 а.е.

12. Задачи

1. Определите массу Сатурна (в массах Земли), если известно, что спутник Сатурна
Титан отстоит от него на расстоянии 1220 тыс. км и обращается с периодом 16 суток.
Дано:
а=1220·103
км
Т=16 суток
ал=384·103 км
Тл=27,3 суток
МЗ=1
МС – ?
Решение:
T M C mT
2
T M З m Л
2
Л
MС
2
Л
2
а
а
3
MC
T
MЗ
T
3
Л
2
Л
2
а3
3
аЛ
а3
T
3 MЗ
T аЛ
27,3суток
M С
16суток
2
3
1220 10 3 км
1 93,4М З
3
384 10 км
Ответ: M С 93,4М З

13. Задачи

1. Расстояние от Земли до Луны в ближайшей к ней точке своей орбиты составляет
363 тыс.км, а в наиболее удаленной точке 405 тыс.км. Определите горизонтальный
параллакс Луны в этих положениях.
Дано:
q=363 тыс.км
Q=405 тыс.км
RЗ=6370 км
p1 – ?
p2 –?
Решение:
206265"
D
RЗ
p"
p
206265"
RЗ
D
206265"
p1
6370 3619,5" 1
363000км
p2
206265"
6370 3244,2" 54'
405000км
Ответ: 1°, 54’

14. Задачи

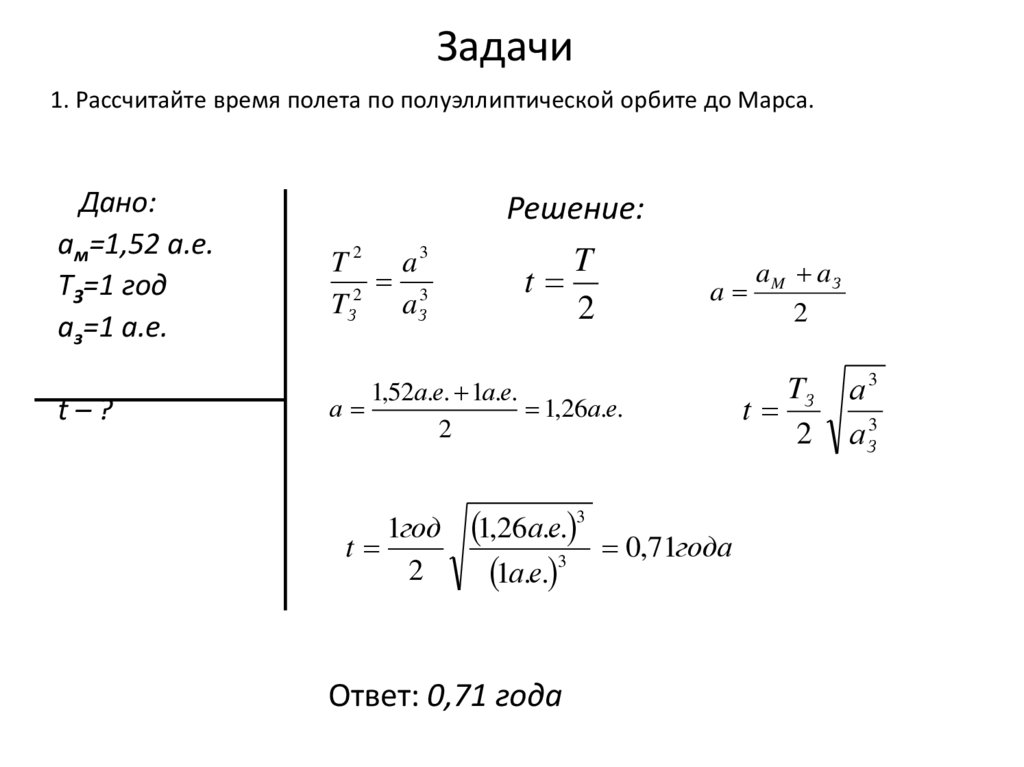
1. Рассчитайте время полета по полуэллиптической орбите до Марса.
Дано:
ам=1,52 а.е.
ТЗ=1 год
аз=1 а.е.
t–?
Решение:
T 2 a3
3
2
TЗ
aЗ
T
t
2
a
1,52а.е. 1а.е.
а
1,26а.е.
2
1год
t
2
1,26а.е. 3
1а.е. 3
Ответ: 0,71 года
0,71года
aM aЗ
2
T
t З
2
а3
а З3

15. Задачи

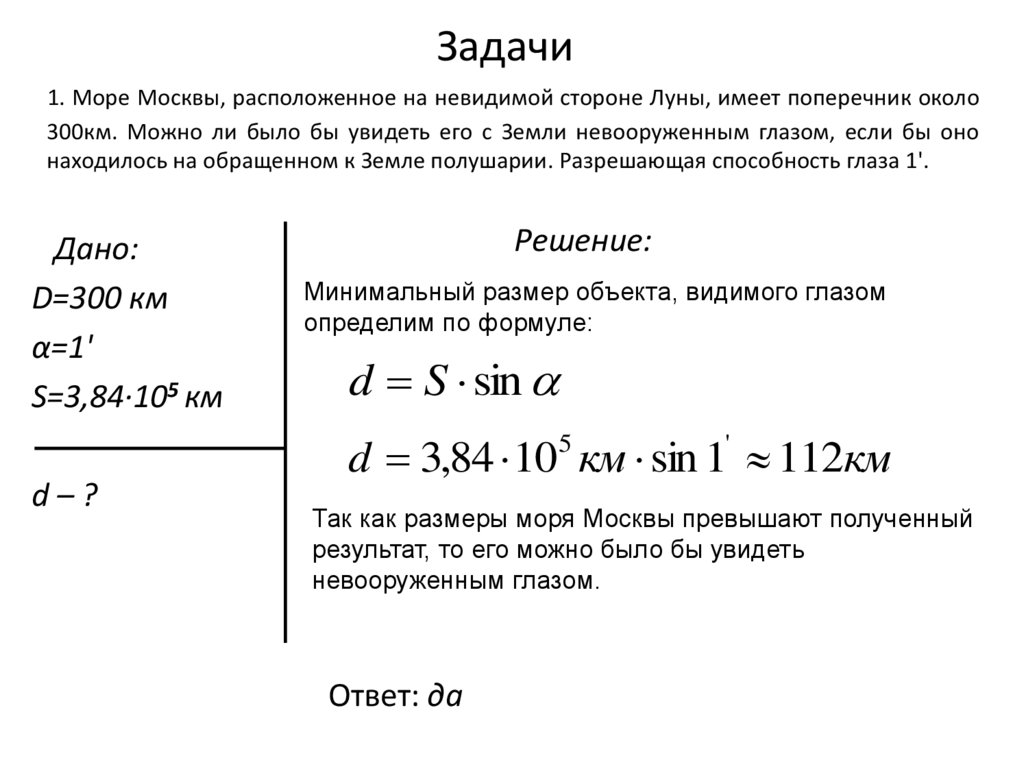
1. Море Москвы, расположенное на невидимой стороне Луны, имеет поперечник около
300км. Можно ли было бы увидеть его с Земли невооруженным глазом, если бы оно
находилось на обращенном к Земле полушарии. Разрешающая способность глаза 1'.
Дано:
D=300 км
α=1'
S=3,84·105 км
d–?
Решение:
Минимальный размер объекта, видимого глазом
определим по формуле:
d S sin
d 3,84 10 5 км sin 1' 112км
Так как размеры моря Москвы превышают полученный
результат, то его можно было бы увидеть
невооруженным глазом.
Ответ: да

16. Задачи

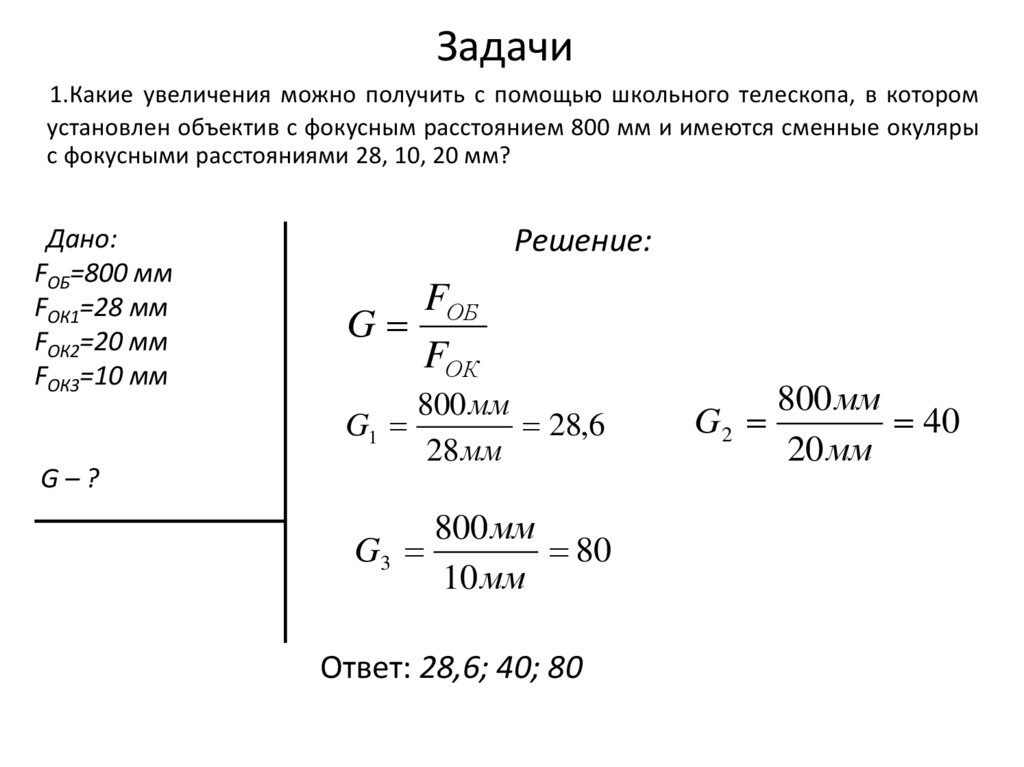
1.Какие увеличения можно получить с помощью школьного телескопа, в котором
установлен объектив с фокусным расстоянием 800 мм и имеются сменные окуляры
с фокусными расстояниями 28, 10, 20 мм?
Дано:
FОБ=800 мм
FОК1=28 мм
FОК2=20 мм
FОК3=10 мм
G–?
Решение:
FОБ
G
FОК
800 мм
G1
28,6
28 мм
800 мм
G3
80
10 мм
Ответ: 28,6; 40; 80
800 мм
G2
40
20 мм

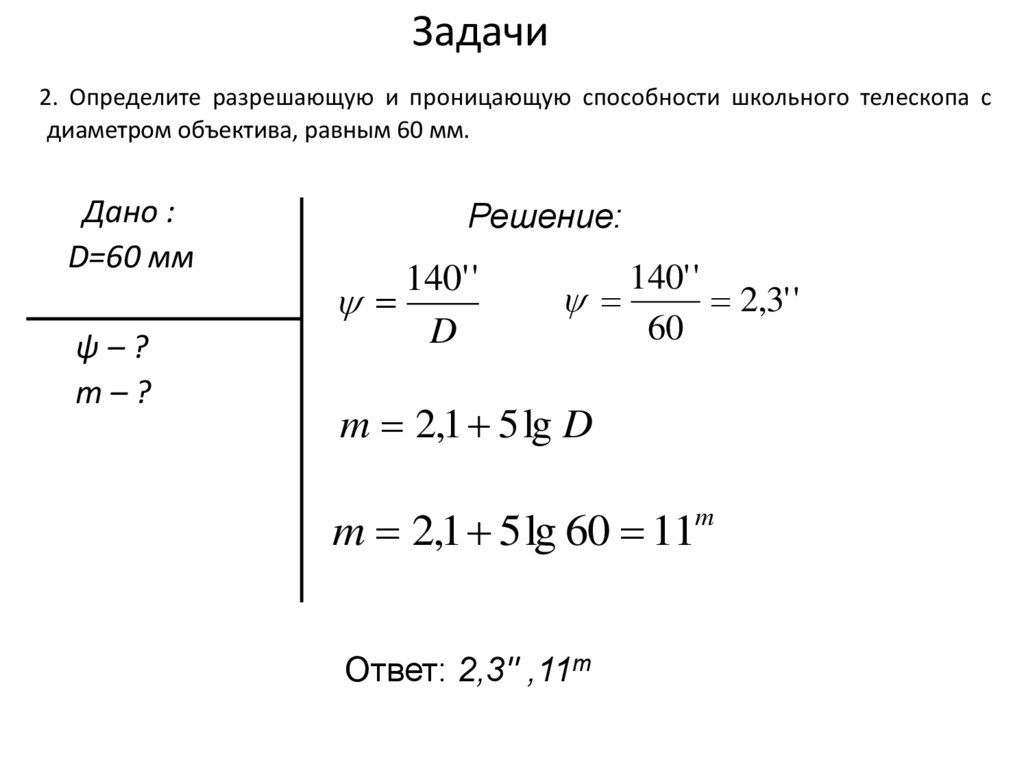
17. Задачи

2. Определите разрешающую и проницающую способности школьного телескопа с
диаметром объектива, равным 60 мм.
Дано :
D=60 мм
ψ–?
m–?
Решение:
140' '
D
140' '
2,3' '
60
m 2,1 5 lg D
m 2,1 5 lg 60 11m
Ответ: 2,3'' ,11m

18. Задачи

1. Линия водорода с длиной волны 434,00 нм на спектрограмме звезды оказалась
равной 434,12 нм. К нам или от нас движется звезда и с какой скоростью?
Решение:
0 r
0
c
Дано:
λ0=434,0 нм
λ=434,12 нм
с=3·105 км/c
(434,12 434,0)нм 0,12нм
r– ?
r
r
0
0,12нм
3 10 5 км с 83 км с
434,0нм
Так как
>0 ,то звезда удаляется.
Ответ: удаляется, 83 км/с
c

19. Задачи

2. Поверхность Солнца близка по своим свойствам к абсолютно черному телу. Определите
температуру солнечной поверхности и мощность излучения единицы поверхности, если
максимум лучеиспускательной способности приходится на длину волны 0,48 мкм.
Дано :
=0,48 мкм
max
b=2900 К·мкм
Т–?
–?
Решение:
b
b
max
T
max
T
2900 К мкм
T
6000 К
0,48 мкм
T 4
5,67 10 8 Вт / м 2 К 4 6000К 4
7,3 10 7 Вт м 2
Ответ: 6000 К, 7,3·107Вт/м2

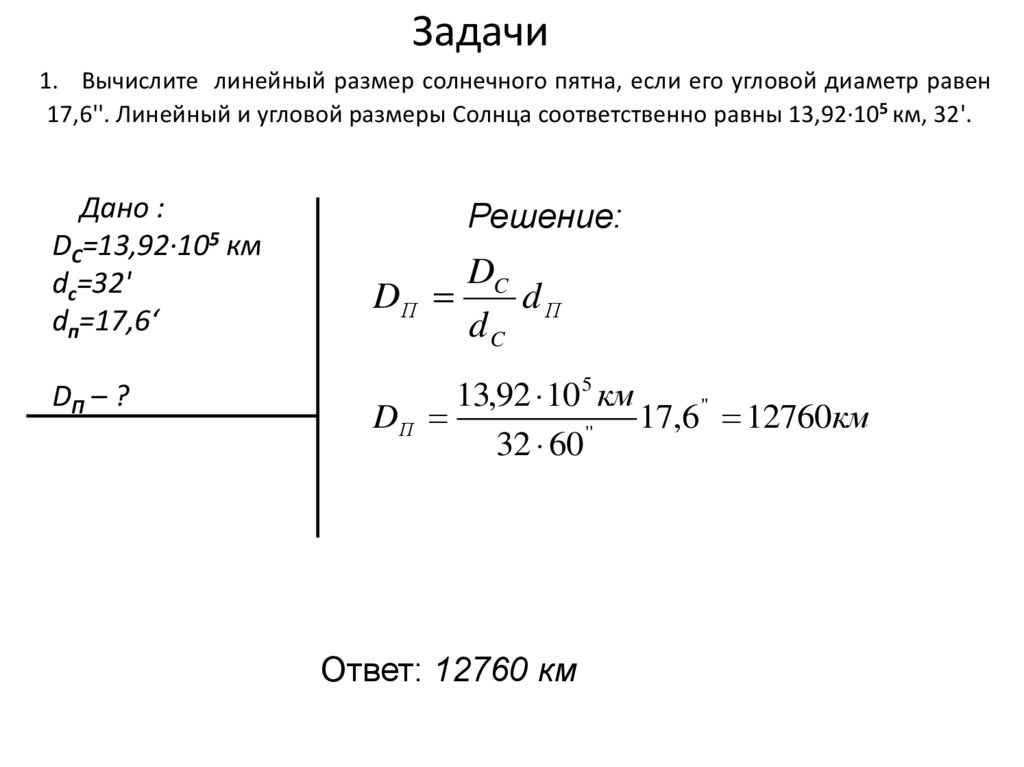
20. Задачи

1. Вычислите линейный размер солнечного пятна, если его угловой диаметр равен
17,6''. Линейный и угловой размеры Солнца соответственно равны 13,92·105 км, 32'.
Дано :
DC=13,92·105 км
dc=32'
dп=17,6‘
DП – ?
Решение:
DC
DП
dП
dC
13,92 10 5 км
''
DП
17
,
6
12760км
''
32 60
Ответ: 12760 км

21. Задачи

2. Определите массу Солнца, если Земля обращается вокруг Солнца на расстоянии 1
а.е. с периодом 1 год. Орбиту Земли считать круговой.
Дано :
ТЗ=1год=
=3,156·107 с
аз=1 а.е. =
=1,496·1011 м
MC – ?
Решение:
Сила всемирного тяготения является центростремительной
M m
m 2
G C2
aЗ
aЗ
2 a З
T
2
M
G 2C
aЗ
aЗ
4 2 a З
MC
GT 2
MC
2 aЗ
G
3
4 3,14 2 (1,496 1011 м) 3
30
MC
2
10
кг
11
2
2
7
2
6,67 10 Н м / кг (3,156 10 с)
Ответ: 2·1030 кг

22. Задачи

1. Новая звезда в момент вспышки имела видимую звездную величину 3,2m.
Вычислите расстояние до нее, если известно, что большинство новых звезд этого
типа имеют абсолютную звездную величину -8m.
Дано:
m=3,2m
M=-8m
Решение:
M m 5 5 lg r
r 10
0 , 2 m M 1
r–?
r 10 0, 2 3, 2 8 1 пк 10 3, 24 пк 1700пк
Ответ: 1700 пк

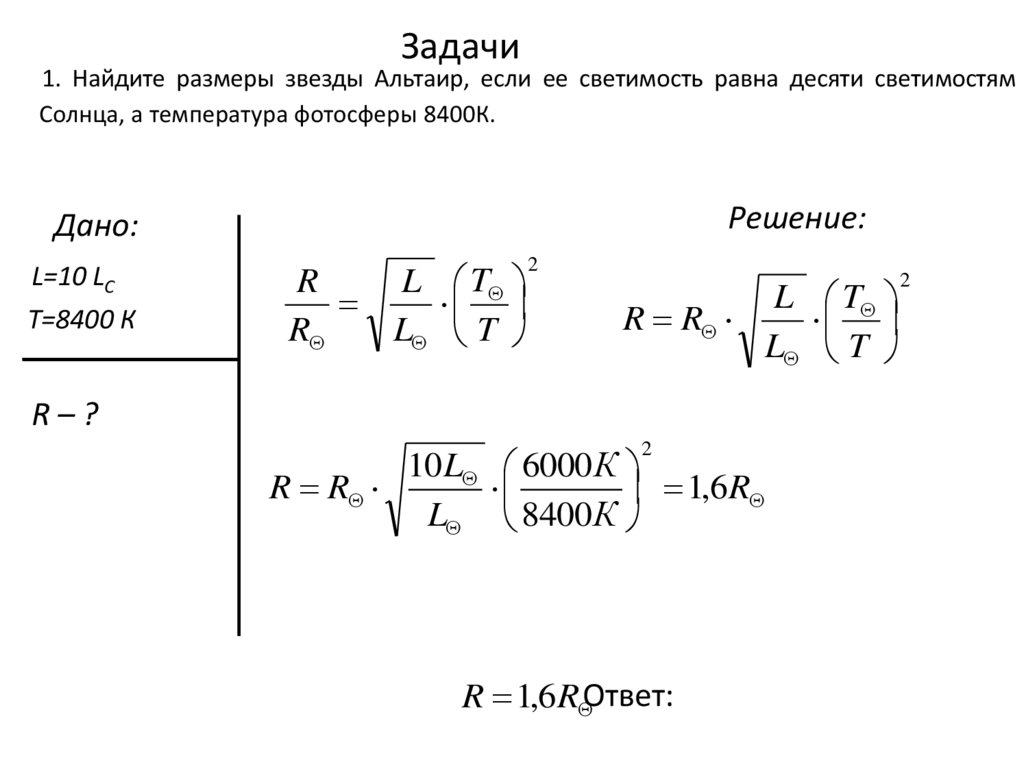
23. Задачи

1. Найдите размеры звезды Альтаир, если ее светимость равна десяти светимостям
Солнца, а температура фотосферы 8400К.
Решение:
Дано:
L=10 LC
T=8400 К
R
R
L T
L T
2
L T
R R
L T
R–?
10 L
R R
L
2
6000 К
1,6 R
8400 К
R 1,6R Ответ:
2

24. Задачи

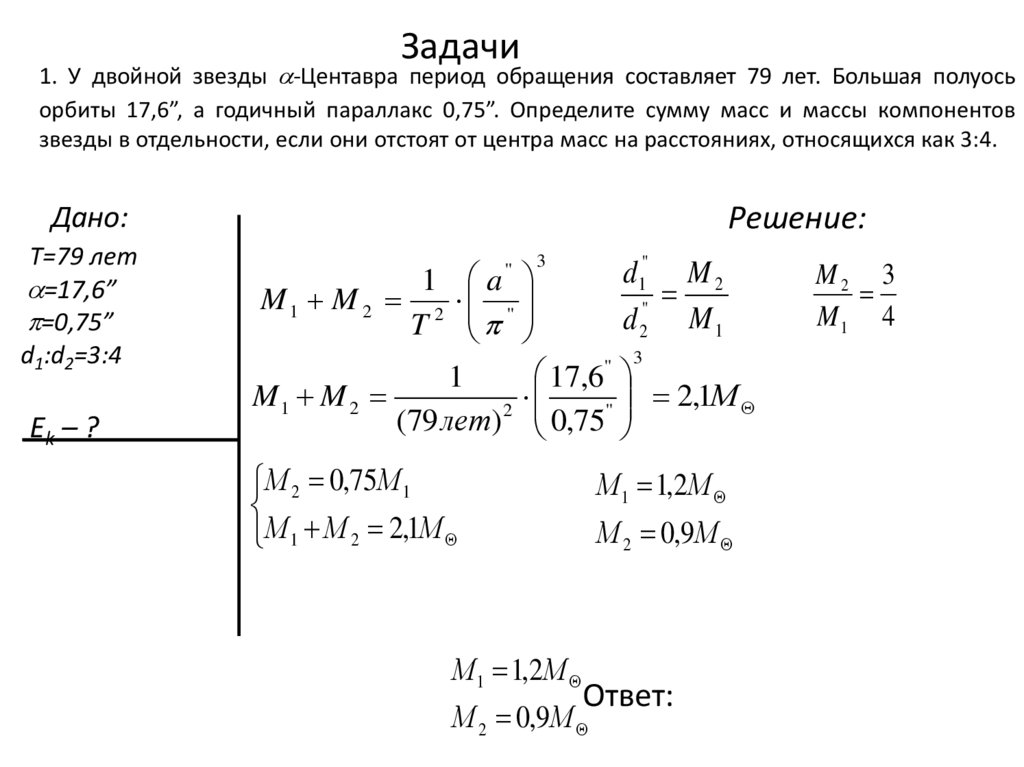
1. У двойной звезды -Центавра период обращения составляет 79 лет. Большая полуось
орбиты 17,6”, а годичный параллакс 0,75”. Определите сумму масс и массы компонентов
звезды в отдельности, если они отстоят от центра масс на расстояниях, относящихся как 3:4.
Решение:
Дано:
Т=79 лет
=17,6”
=0,75”
d1:d2=3:4
Ek – ?
''
'' 3
d
M2
1
a
1
M 1 M 2 2 ''
''
d2 M1
T
'' 3
17,6
1
2,1М
M1 M 2
2
''
(79 лет) 0,75
М 2 0,75М 1
М 1 М 2 2,1М
М 1 1,2М
М 1 1,2М
М 2 0,9М
Ответ:
М 2 0,9М
M2 3
M1 4

25. Задачи

1. При изучении масс звезд и их светимостей установлено, что для звезд, принадлежащих к
главной последовательности, в интервале от 0,5МС до 10МС светимость пропорциональна
четвертой степени ее массы. Проведите необходимые расчеты и укажите на диаграмме
местонахождение звезд.
Дано:
МЗ1=0,5 МС
L–?
M–?
Решение:
L L M З
L
2,512 M M
L
4
L
M M 2,5 lg
L
L
M 5 2,5 lg
L
L L 0,54 6,25 10 2 L
M 5 2,5 lg 0,0625 8 m
Ответ: L=0,0625 LС, М=8m

26. Задачи

2. Какова средняя плотность красного сверхгиганта, если его диаметр в 300 раз
больше солнечного, а масса в 30 раз больше, чем масса Солнца?
Дано:
D2=300D1
M2=30M1
ρ2 – ?
М
3M
6M
V
4 R 3 D 3
2
30
6
1
,
1
10
1 (300) 3
Решение:
6M 2
M2
2 D23
M1
3
1 6 M 1
D2
D13
D13
2 1,1 10 6 1,1 10 6 1,4 103 кг м3 1,6 10 3 кг м3
Ответ: 1,6·10-3 кг/м3

27. Задачи

1. У звезды Альтаир годичный параллакс равен 0,198”,собственное движение 0,658”
и лучевая скорость –26,3 км/с. Определите тангенциальную и пространственную
скорости звезды.
Дано:
=0,198”
=0,658”
=-26,3 км/с
–?
–?
Решение:
"
4,74 ''
4,74
2 r2
0,658' '
15,8 км с
0,198' '
(15,8км / с) 2 ( 23,6км / с) 2 30,7км / с
Ответ: 15,8 км/с; 30,7 км/с

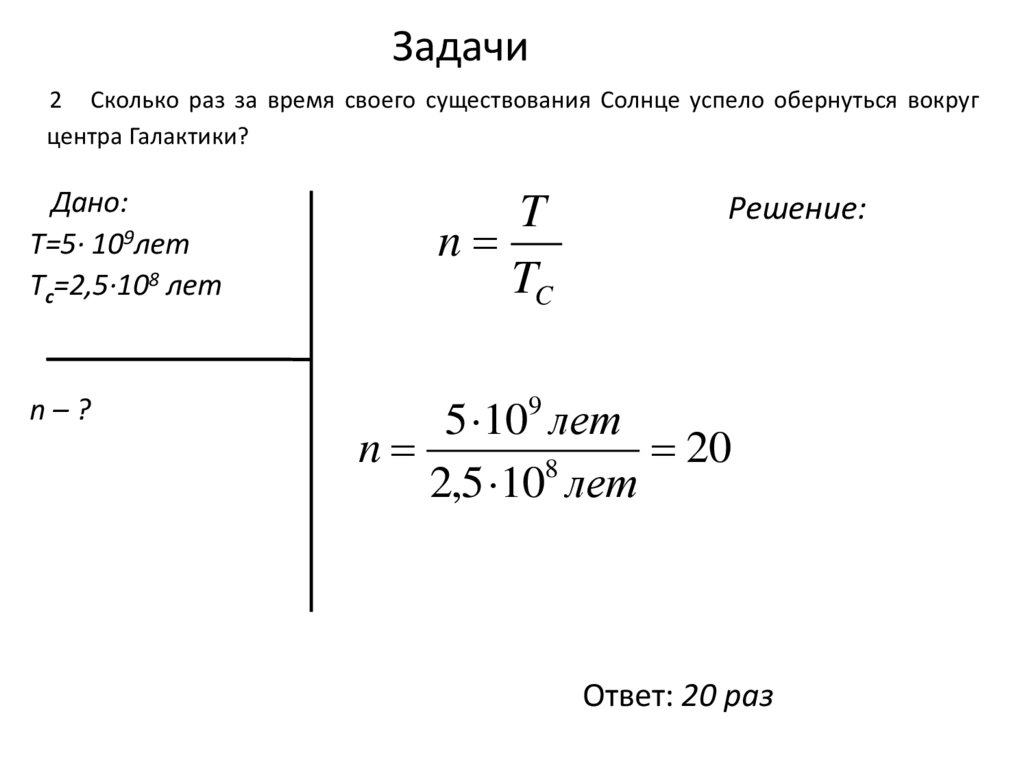
28. Задачи

2 Сколько раз за время своего существования Солнце успело обернуться вокруг
центра Галактики?
Дано:
Т=5· 109лет
Тс=2,5·108 лет
n–?
T
n
TC
Решение:
5 10 лет
n
20
8
2,5 10 лет
9
Ответ: 20 раз

29. Задачи

1. Определите массу Большой газопылевой туманности в Орионе, если ее видимые
размеры составляют около 1 , а расстояние до нее 400пк , а плотность газопылевой
среды 10-19 кг/м3.
Дано:
=1
r=400 пк
ρ=10 -19кг/м3
Решение:
4 3
R r sin
M R
2
3
R 400пк sin 0,5 3,5пк
М–?
M
4
3,14 (3,5 3 1016 м) 3 10 19 кг м 3 4,8 10 32 кг 240М
3
Ответ: 240 МС

30. Задачи

2 Планетарная туманность в созвездии Лиры имеет угловой диаметр 83’’ и
находится от нас на расстоянии в 660пк. Каковы ее линейные размеры в
астрономических единицах?
Дано:
d=83’’
r=660пк
D–?
d ' ' r
D
206265' '
Решение:
83' ' 660пк
D
0,27 пк
206265' '
1пк 206265а.е.
D 0,27 206265а.е. 55691,6а.е.
Ответ: 0,27пк, 55691,6 а.е.

31. Задачи

2. Галактика удаляется от нас со скоростью 6000км/с и имеет видимый угловой
размер 2’. Определите расстояние до галактики и ее линейные размеры.
Дано:
r=6·103км/с
=2’=0,033
D–?
d–?
r HD
D
r
Решение:
H
6 103 км / с
D
80Мпк
75 км / с Мпк
d D sin
d 80 106 пк sin 0,033 4,7 104 пк
Ответ: 80 Мпк, 47 кпк

32. Задачи

1. В спектре галактики, которая имеет видимую звездную величину 15,2 , линия водорода
m
( 0=656,3нм) смещена к красному концу спектра на =21,9нм. Вычислите скорость
удаления галактики, расстояние до нее, абсолютную звездную величину и светимость
галактики.
Дано:
m=15,2m
0=656,3нм
=21,9нм
r – ?
r–?
L–?
M–?
r
0
Решение:
c
r
21,9нм
3 105 км / с 10 4 км / с
656,3нм
r
4
10
км / с
r
r
133Мпк
H
75 км / с Мпк
М m 5 5 lg r
М 15,2 5 5 lg( 1,33 108 пк) 20,4m
L 2,512 4,8 m L
L 2,512 4,8 20, 4 L 1,2 1010 L
Ответ: 104км/с; 133 Мпк;
1,2·1010LC; -20,4m

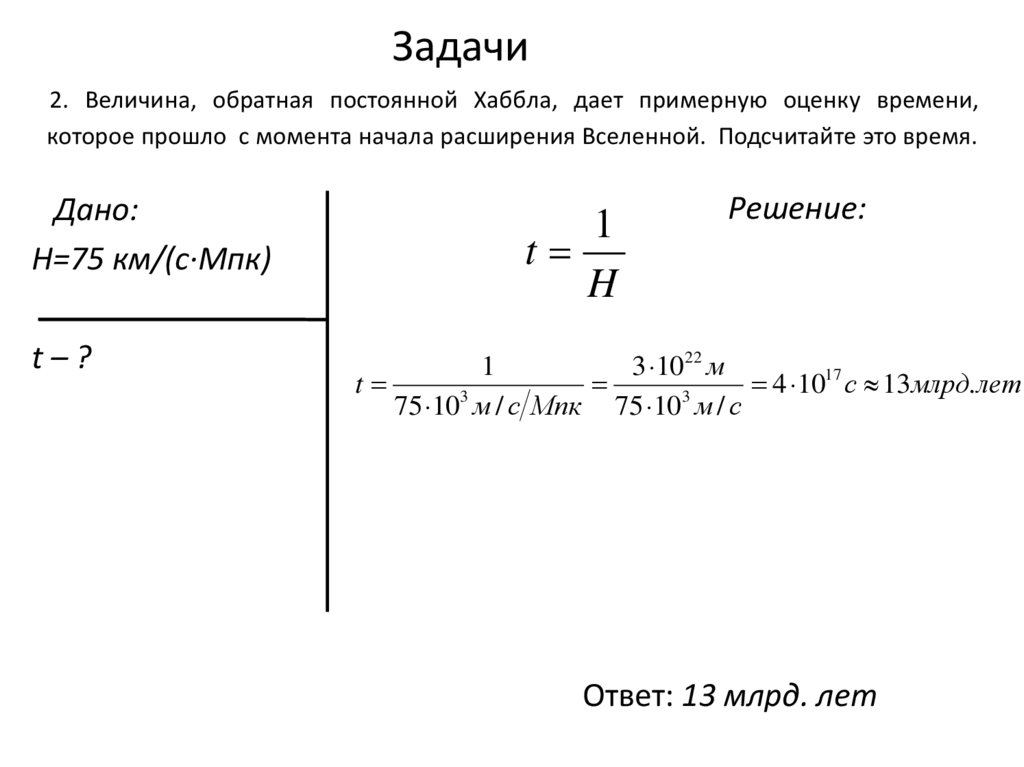
33. Задачи

2. Величина, обратная постоянной Хаббла, дает примерную оценку времени,
которое прошло с момента начала расширения Вселенной. Подсчитайте это время.
Дано:
H=75 км/(с·Мпк)
t–?
1
t
H
Решение:
1
3 1022 м
17
t
4
10
с 13 млрд.лет
75 103 м / с Мпк 75 103 м / с
Ответ: 13 млрд. лет

34. Задачи

1. Представьте, что на радиосигнал, принятый от цивилизации из галактики
М 106,
нами в адрес этой цивилизации отправлена ответная радиограмма. Сколько времени
пришлось бы ждать ответа на нее, если расстояние до галактики М 106 составляет 10Мпк?
Дано:
r=10 Мпк
t–?
Решение:
2r
t
c
2 10 106 3 1013 км
15
7
t
2
10
с
6
,
5
10
лет
5
3 10 км / с
Ответ: 65 млн.лет

35. Задачи

2. Какое время (по счету на Земле) отец должен пробыть в космическом полете со
скоростью 0,9с, чтобы после возвращения на Землю сравняться по возрасту со своим
сыном? Возраст отца при отправке в полет принять равным 25 годам, сына – 1 году.
Дано:
=0,9с
tc=1 год
to=25лет
tз – ?
tc t з to t з 1
2
с2
Решение:
tз
to tc
1 1
tз
25 лет 1год
(0,9с)
1 1 2
с
2
42,5года
Ответ: 42,5 года
2
с2

36.

7-8 класс
1. Марс удобнее всего изучать во время противостояния, когда
Земля находится между Марсом и Солнцем. Определите, через
какой промежуток времени повторяются противостояния Земли и
Марса. Марс совершает оборот вокруг Солнца за 687 земных
дней, а Земля – за 365 дней.

37.

7-8 класс
1. Марс удобнее всего изучать во время противостояния, когда
Земля находится между Марсом и Солнцем. Определите, через
какой промежуток времени повторяются противостояния Земли и
Марса. Марс совершает оборот вокруг Солнца за 687 земных
дней, а Земля – за 365 дней.
Решение:
За промежуток времени T от одного противостояния до другого
Марс совершает k оборотов, а Земля (k + 1) оборот (k не
обязательно целое). Этот промежуток времени выражается через
периоды обращения Земли и Марса вокруг Солнца TЗ и TМ
следующим образом: T = (k + 1)TЗ - kTМ. Отсюда находим k =
TЗ/(TМ − TЗ) и T = TЗTМ/(TМ − TЗ).
Подставляя численные значения TЗ и TМ, получаем T ≈ 779 дней.

38.

39.

40.

41.

9 класс.
2. Солнце находится на расстоянии 7,5 кпк от центра Галактики и
вот уже 4.6 млрд. лет движется со скоростью 220 км/с. Чему равен
галактический год? Сколько галактических лет Солнцу?
16
2πR
Решение: Т =
2 ⋅3,14 ⋅7500 ⋅3⋅10 м
=
V
220000м / с
16
0,64 ⋅10 c
16
0,64 ⋅10 c
6
≈ 200 ⋅10 лет
7
3,15 ⋅10 c / год
Зная возраст Солнца около 4.6 млрд. лет, 4.6/0.2 = 23
Ответ: примерно 23 года (с точностью до знания возраста Солнца)

42.

43.

10 класс
3. Радиус одного из астероидов составляет 5 км. Его плотность составляет
5,5 г/см3. Определите ускорение свободного падения на его поверхности.
Определите, на какую высоту поднялся бы человек, находящийся на
астероиде и подпрыгнувший с усилием, достаточным для прыжка на высоту
5 см на Земле. Считайте, что астероид имеет форму шара.
Решение:
Пусть Ма – масса астероида. С учетом закона всемирного тяготения и
второго закона Ньютона ускорение свободного падения
на астероиде
(1). Представим массу астероида через объем
шара и плотность:
, отсюда
м/с2. По
условию задачи человек в момент прыжка на Земле и на астероиде обладает
одной и той же кинетической энергией. Поэтому потенциальная энергия в
высшей точке подъема как на Земле, так и на астероиде будет одинакова:
, откуда
. Полученное значение не является
точным: на самом деле прыжок будет выше, так как значение ускорения
свободного падения убывает с высотой по закону, даваемому формулой (1).

44.

45.

46.

Определите массу Юпитера в массах Земли,
путём сравнения системы Юпитер – Европа с
системой Земля – Луна, если известно, что
спутник Европа отстоит от него на расстоянии
671 тыс. км и обращается с периодом 3,55 суток.

47.

Определите массу Юпитера в массах Земли, путём
сравнения системы Юпитер – Европа с системой Земля –
Луна, если известно, что спутник Европа отстоит от него на
расстоянии 671 тыс. км и обращается с периодом 3,55
суток.
Дано:
Т1=3,55 сут
Т2=27,3 сут
а1=671000км
T22 a13
M1 2 3 M З
а2=384000км
T1 a 2
М2=1
М1– ?
2
27,3сут (671000км) 3
M1
MЗ
2
3
3,55сут 384000км
Ответ: 316 масс Земли
316М З