Решение астрономических задач. Полное решение всех типов задач по астрономии

1. Решение астрономических задач

полное решение всех
типов задач по астрономии

2. Задачи

1. В местный полдень путешественник отметил 14 ч 13 мин по гринвичскому
времени. Определите географическую долготу места наблюдения.
Дано:
Т =12 ч
Т0=14ч 13 мин
–?
Решение:
Т λ = Т0 + λ
λ = Т λ -Т0
λ=12 ч -14 ч 13 мин = 2 ч 13 мин з.д.
Ответ: 2 ч 13 мин з.д.

3. Задачи

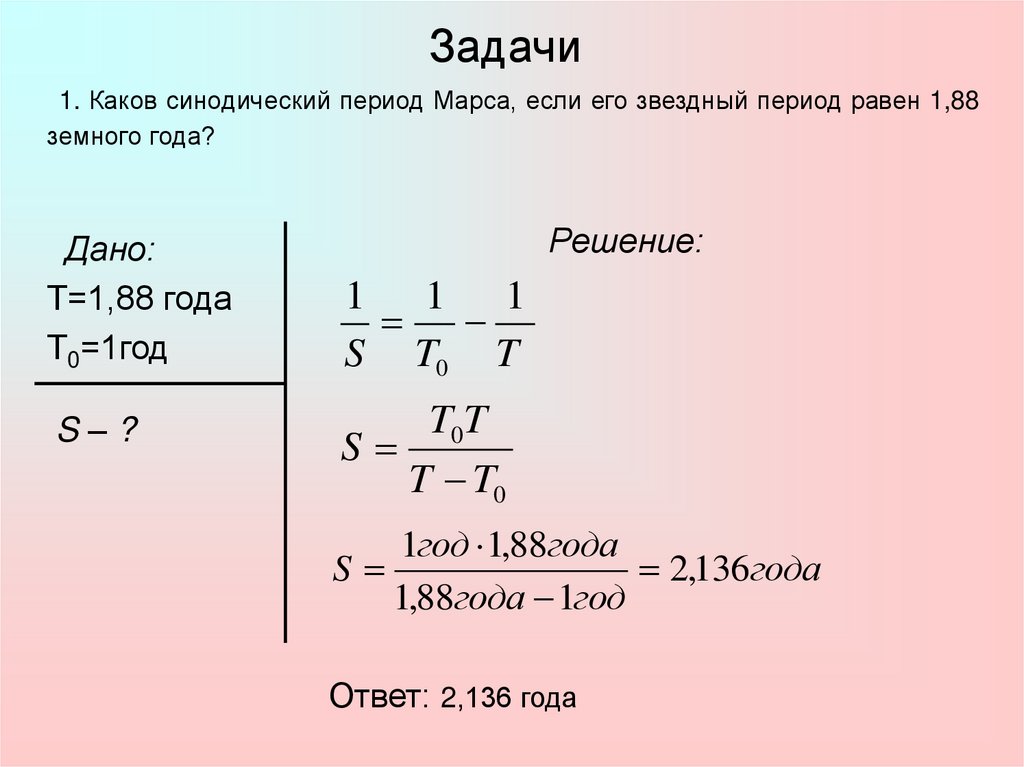
1. Каков синодический период Марса, если его звездный период равен 1,88
земного года?
Дано:
Т=1,88 года
Т0=1год
S–?
Решение:
1 1 1
S T0 T
T0T
S
T T0
1год 1,88года
S
2,136года
1,88года 1год
Ответ: 2,136 года

4. Задачи

1. Определите афелийное расстояние астероида Минск, если большая
полуось его орбиты равна 2,88 а.е., а эксцентриситет составляет 0,24.
Дано:
а=2,88 а.е.
е =0,24
Решение:
Q a 1 e
Q 2,88 1 0,24 3,57а.е.
Q–?
Ответ: 3,57 а.е.

5. Задачи

2. Определите среднее расстояние от Юпитера до
2 Солнца,
3 если известно, что
его звездный период обращения вокруг Солнца равен 11,86 года.
2
3
з
Дано :
Решение:З
2
3
2
Т= 11,86 года
T
a
T
a
ТЗ =1 год
аз=1 а.е.
T
a
3
2
TЗ
aз
a aз 3
2
а–?
T
TЗ2
T
a aз 3 2
2
(
11
,
86
года
)
a 1а.е.3 TЗ
5,2а.е.
2
(1год)
Ответ: 5,2 а.е.

6. Задачи

1. Определите массу Сатурна (в массах Земли), если известно, что спутник
Сатурна Титан отстоит от него на расстоянии 1220 тыс. км и обращается с
периодом 16 суток.
Дано:
а=1220·103 км
Т=16 суток
ал=384·103 км
Тл=27,3 суток
МЗ=1
МС – ?
Решение:
T M C mT
2
T M З mЛ
2
Л
MС
2
Л
2
а
а
3
MC
T
MЗ
T
3
Л
2
Л
2
а3
3
аЛ
а3
T
3 MЗ
T аЛ
27,3суток
M С
16суток
2
3
1220 10 3 км
1 93,4М З
3
384 10 км
Ответ: M С 93,4М З

7. Задачи

1. Расстояние от Земли до Луны в ближайшей к ней точке своей орбиты
составляет
363 тыс.км, а в наиболее удаленной точке 405 тыс.км.
Определите горизонтальный параллакс Луны в этих положениях.
Дано:
q=363 тыс.км
Q=405 тыс.км
RЗ=6370 км
p1 – ?
p2 –?
Решение:
206265"
D
RЗ
p"
p
206265"
RЗ
D
206265"
p1
6370 3619,5" 1
363000км
p2
206265"
6370 3244,2" 54'
405000км
Ответ: 1°, 54’

8. Задачи

1. Рассчитайте время полета по полуэллиптической орбите до Марса.
Дано:
ам=1,52 а.е.
ТЗ=1 год
аз=1 а.е.
t–?
T 2 a3
3
2
TЗ
aЗ
Решение:
T
a aЗ
t
a M
2
2
1,52а.е. 1а.е.
а
1,26а.е.
2
1год
t
2
1,26а.е. 3
1а.е. 3
Ответ: 0,71 года
0,71года
T
t З
2
а3
а З3

9. Задачи

1. Море Москвы, расположенное на невидимой стороне Луны, имеет
поперечник около 300км. Можно ли было бы увидеть его с Земли
невооруженным глазом, если бы оно находилось на обращенном к Земле
полушарии. Разрешающая способность глаза 1'.
Дано:
D=300 км
α=1'
S=3,84·105 км
d–?
Решение:
Минимальный размер объекта, видимого глазом
определим по формуле:
d S sin
d 3,84 10 5 км sin 1' 112км
Так как размеры моря Москвы превышают полученный
результат, то его можно было бы увидеть
невооруженным глазом.
Ответ: да

10. Задачи

1.Какие увеличения можно получить с помощью школьного телескопа, в
котором установлен объектив с фокусным расстоянием 800 мм и имеются
сменные окуляры с фокусными расстояниями 28, 10, 20 мм?
Дано:
FОБ=800 мм
FОК1=28 мм
FОК2=20 мм
FОК3=10 мм
G–?
Решение:
FОБ
G
FОК
800 мм
G1
28,6
28 мм
800 мм
G3
80
10 мм
Ответ: 28,6; 40; 80
800 мм
G2
40
20 мм

11. Задачи

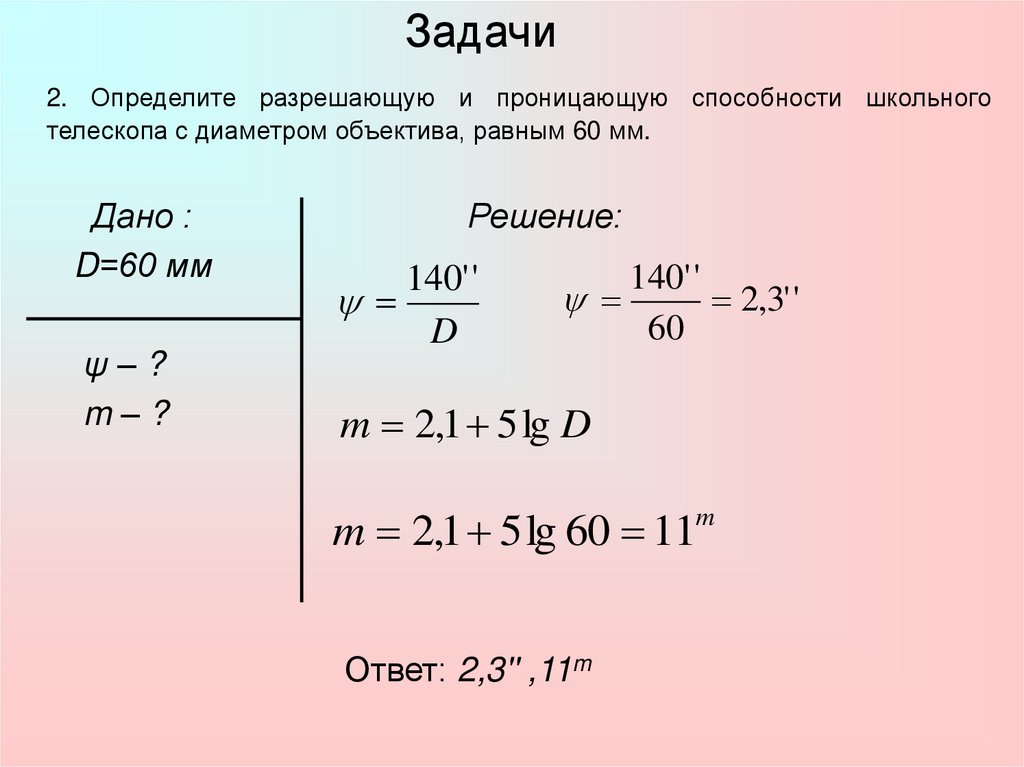
2. Определите разрешающую и проницающую способности школьного
телескопа с диаметром объектива, равным 60 мм.
Дано :
D=60 мм
ψ–?
m–?
Решение:
140' '
D
140' '
2,3' '
60
m 2,1 5 lg D
m 2,1 5 lg 60 11m
Ответ: 2,3'' ,11m

12. Задачи

1. Линия водорода с длиной волны 434,00 нм на спектрограмме звезды
оказалась равной 434,12 нм. К нам или от нас движется звезда и с какой
скоростью?
Решение:
Дано:
λ0=434,0 нм
λ=434,12 нм
с=3·105 км/c
(434,12 434,0)нм 0,12нм
r – ?
r
0 r
0
c
r
0
0,12нм
3 10 5 км с 83 км с
434,0нм
Так как
>0 ,то звезда удаляется.
Ответ: удаляется, 83 км/с
c

13. Задачи

2. Поверхность Солнца близка по своим свойствам к абсолютно черному
телу. Определите температуру солнечной поверхности и мощность излучения
единицы поверхности, если максимум лучеиспускательной способности
приходится на длину волны 0,48 мкм.
Дано :
max =0,48 мкм
b=2900 К·мкм
Т–?
–?
Решение:
b
b
max
T
max
T
2900 К мкм
T
6000 К
0,48 мкм
T 4
5,67 10 8 Вт / м 2 К 4 6000К 4
7,3 10 7 Вт м 2
Ответ: 6000 К, 7,3·107Вт/м2

14. Задачи

1. Вычислите линейный размер солнечного пятна, если его угловой диаметр
равен 17,6''. Линейный и угловой размеры Солнца соответственно равны
13,92·105 км, 32'.
Дано :
DC=13,92·105 км
dc=32'
dп=17,6‘
DП – ?
Решение:
DC
DП
dП
dC
13,92 10 5 км
''
DП
17
,
6
12760км
''
32 60
Ответ: 12760 км

15. Задачи

2. Определите массу Солнца, если Земля обращается вокруг Солнца на
расстоянии 1 а.е. с периодом 1 год. Орбиту Земли считать круговой.
Дано :
ТЗ=1год=
=3,156·107 с
аз=1 а.е. =
=1,496·1011 м
MC – ?
Решение:
Сила всемирного тяготения является центростремительной
M m
m 2
G C2
aЗ
aЗ
2 a З
T
2
M
G 2C
aЗ
aЗ
4 2 a З
MC
GT 2
MC
2 aЗ
G
3
4 3,14 2 (1,496 1011 м) 3
30
MC
2
10
кг
11
2
2
7
2
6,67 10 Н м / кг (3,156 10 с)
Ответ: 2·1030 кг

16. Задачи

1. Новая звезда в момент вспышки имела видимую звездную величину 3,2m.
Вычислите расстояние до нее, если известно, что большинство новых
звезд этого типа имеют абсолютную звездную величину -8m.
Дано:
m=3,2m
M=-8m
Решение:
M m 5 5 lg r
r 10
0 , 2 m M 1
r–?
r 10 0, 2 3, 2 8 1 пк 10 3, 24 пк 1700пк
Ответ: 1700 пк

17. Задачи

1. Найдите размеры звезды Альтаир, если ее светимость равна десяти
светимостям Солнца, а температура фотосферы 8400К.
Решение:
Дано:
L=10 LC
T=8400 К
R
R
L T
L T
2
L T
R R
L T
R–?
10 L
R R
L
2
6000 К
1,6 R
8400 К
Ответ: R 1,6 R
2

18. Задачи

1. У двойной звезды -Центавра период обращения составляет 79 лет.
Большая полуось орбиты 17,6”, а годичный параллакс 0,75”. Определите сумму
масс и массы компонентов звезды в отдельности, если они отстоят от центра
масс на расстояниях, относящихся как 3:4.
Решение:
Дано:
Т=79 лет
=17,6”
=0,75”
d1:d2=3:4
Ek – ?
''
'' 3
d
M2
1
a
1
M 1 M 2 2 ''
''
d2 M1
T
'' 3
17,6
1
2,1М
M1 M 2
2
''
(79 лет) 0,75
М 2 0,75М1
М1 М 2 2,1М
Ответ:
М 1 1,2М
М 2 0,9М
М 1 1,2М
М 2 0,9М
M2 3
M1 4

19. Задачи

1. При изучении масс звезд и их светимостей установлено, что для звезд,
принадлежащих к главной последовательности, в интервале от 0,5МС до 10МС
светимость пропорциональна четвертой степени ее массы. Проведите
необходимые расчеты и укажите на диаграмме местонахождение звезд.
Дано:
МЗ1=0,5 МС
L–?
M–?
Решение:
L L M З
4
L
M M 2,5 lg
L
L
2,512 M M
L
L
M 5 2,5 lg
L
L L 0,54 6,25 10 2 L
M 5 2,5 lg 0,0625 8 m
Ответ: L=0,0625 LС, М=8m

20. Задачи

2. Какова средняя плотность красного сверхгиганта, если его диаметр в 300
раз больше солнечного, а масса в 30 раз больше, чем масса Солнца?
Дано:
D2=300D1
M2=30M1
ρ2 – ?
Решение:
М
3M
6M
3
V
4 R
D 3
2
30
6
1
,
1
10
1 (300)3
6M 2
M2
2 D23
M1
3
1 6 M 1
D2
D13
D13
2 1,1 10 6 1,1 10 6 1,4 103 кг м3 1,6 10 3 кг м3
Ответ: 1,6·10-3 кг/м3

21. Задачи

1. У звезды Альтаир годичный параллакс равен 0,198”,собственное
движение 0,658” и лучевая скорость –26,3 км/с. Определите тангенциальную
и пространственную скорости звезды.
Дано:
=0,198”
=0,658”
=-26,3 км/с
–?
–?
Решение:
"
4,74 ''
4,74
2 r2
0,658' '
15,8 км с
0,198' '
(15,8км / с) 2 ( 23,6км / с) 2 30,7км / с
Ответ: 15,8 км/с; 30,7 км/с

22. Задачи

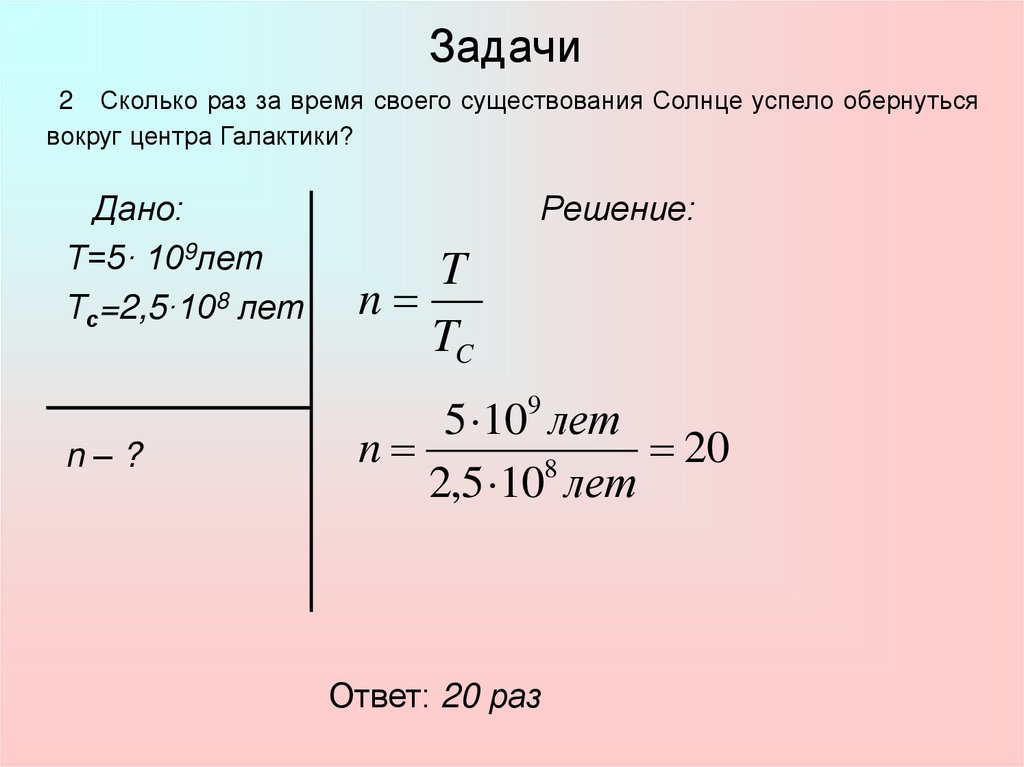
2 Сколько раз за время своего существования Солнце успело обернуться
вокруг центра Галактики?
Дано:
Т=5· 109лет
Тс=2,5·108 лет
Решение:
T
n
TC
5 10 лет
n
20
8
2,5 10 лет
9
n–?
Ответ: 20 раз

23. Задачи

1. Определите массу Большой газопылевой туманности в Орионе, если ее
видимые размеры составляют около 1 , а расстояние до нее 400пк , а
плотность газопылевой среды 10-19 кг/м3.
Дано:
=1
r=400 пк
ρ=10 -19кг/м3
М–?
Решение:
4 3
R r sin
M R
2
3
R 400пк sin 0,5 3,5пк
M
4
3,14 (3,5 3 1016 м) 3 10 19 кг м 3 4,8 10 32 кг 240М
3
Ответ: 240 МС

24. Задачи

2 Планетарная туманность в созвездии Лиры имеет угловой диаметр 83’’ и
находится от нас на расстоянии в 660пк. Каковы ее линейные размеры в
астрономических единицах?
Дано:
d=83’’
r=660пк
Решение:
d ' ' r
D
206265' '
83' ' 660пк
D
0,27пк
206265' '
D–?
1пк 206265а.е.
D 0,27 206265а.е. 55691,6а.е.
Ответ: 0,27пк, 55691,6 а.е.

25. Задачи

2. Галактика удаляется от нас со скоростью 6000км/с и имеет видимый
угловой размер 2’. Определите расстояние до галактики и ее линейные
размеры.
Дано:
r=6·103км/с
=2’=0,033
D–?
d–?
Решение:
r HD
D
r
H
6 103 км / с
D
80Мпк
75 км / с Мпк
d D sin
d 80 106 пк sin 0,033 4,7 104 пк
Ответ: 80 Мпк, 47 кпк

26. Задачи

1. В спектре галактики, которая имеет видимую звездную величину 15,2m,
линия водорода ( 0=656,3нм) смещена к красному концу спектра на =21,9нм.
Вычислите скорость удаления галактики, расстояние до нее, абсолютную
звездную величину и светимость галактики.
Дано:
m=15,2m
0=656,3нм
=21,9нм
r – ?
r–?
L–?
M–?
r
0
Решение:
c
r
21,9нм
3 105 км / с 104 км / с
656,3нм
r
4
10
км / с
r
r
133Мпк
H
75 км / с Мпк
М m 5 5 lg r
М 15,2 5 5 lg( 1,33 108 пк) 20,4m
L 2,512 4,8 m L
L 2,512 4,8 20, 4 L 1,2 1010 L
Ответ: 104км/с; 133 Мпк;
1,2·1010LC; -20,4m

27. Задачи

2. Величина, обратная постоянной Хаббла, дает примерную оценку
времени, которое прошло с момента начала расширения Вселенной.
Подсчитайте это время.
Дано:
H=75 км/(с·Мпк)
t–?
Решение:
1
t
H
1
3 1022 м
17
t
4
10
с 13 млрд.лет
75 103 м / с Мпк 75 103 м / с
Ответ: 13 млрд. лет

28. Задачи

1. Представьте, что на радиосигнал, принятый от цивилизации из галактики
М
106, нами в адрес этой цивилизации отправлена ответная радиограмма. Сколько
времени пришлось бы ждать ответа на нее, если расстояние до галактики М 106
составляет 10Мпк?
Дано:
r=10 Мпк
t–?
Решение:
2r
t
c
2 10 106 3 1013 км
15
7
t
2
10
с
6
,
5
10
лет
5
3 10 км / с
Ответ: 65 млн.лет

29. Задачи

2. Какое время (по счету на Земле) отец должен пробыть в космическом
полете со скоростью 0,9с, чтобы после возвращения на Землю сравняться по
возрасту со своим сыном? Возраст отца при отправке в полет принять равным
25 годам, сына – 1 году.
Дано:
=0,9с
tc=1 год
to=25лет
tз – ?
Решение:
tc t з to t з 1
tз
25 лет 1год
(0,9с)
1 1 2
с
2
Ответ: 42,5 года
2
с
2
tз
42,5года
to tc
1 1
2
с2

30. Успехов!