Основные понятия моделирования химических производств

1. Основные понятия моделирования химических производств

2. Основные понятия и определения

Моделирование - процесс создания модели, ее исследование и
распространение результатов исследования на оригинал.
Оригинал - интересующий нас объект
Модель – изучаемый нами объект.
Цель моделирования – определение оптимальных условий протекания
процесса.
Область применения моделирования:
-
научные исследования;
-
проектирование новых и совершенствование действующих процессов,
аппаратов и производств.
Применение моделирования позволяет осуществить:
-
оптимальное проектирование новых и оптимизацию действующих
процессов;
-
ускорение переноса результатов исследований на производство;
-
решение задач исследования и реализация процессов, которые другими
методами реализовать не удается.

3. Методы моделирования и область их применения

Физическое моделирование (ФМ) - метод исследования на моделях,
имеющих одинаковую с оригиналом физическую природу и
воспроизводящих весь комплекс свойств изучаемых явлений.
Преимущества ФМ:
- полное воспроизводство процесса;
- наглядность процесса;
- возможность регистрации наблюдений без преобразующих устройств;
- изучение явлений, неподдающихся математическому описанию.
Недостатки ФМ:
- для исследования каждого нового процесса необходимо создавать новую
модель;
- изменение параметров оригинала часто требует физической переделки
или полной замены модели;
- высокая стоимость изготовления моделей сложных объектов;
- в ряде случаев имеет ограничения или вообще неприменимо.

4. Математическое моделирование (ММ)

Математическое моделирование – изучение свойств объекта на
математической модели.
Математическая модель – приближенное описание процесса или явления с
помощью математической символики.
Преимущества ММ:
- позволяет осуществить с помощью одного устройства решение целого
класса задач, имеющих одинаковое математическое описание;
- обеспечивает простоту перехода от одной задачи к другой, введение
переменных параметров, возмущений и различных граничных условий;
- дает возможность моделирования по частям (по элементарным процессам);
- использует эффективное средство исследования процессов – ЭВМ, которое
непрерывно совершенствуется;
- экономичнее физического моделирования как по затратам времени, так и по
стоимости.
Существенный недостаток – трудоемкость детального описания свойств
изучаемой сложной химической системы с помощью современного
математического аппарата.

5. Классификация моделей по временно-пространственному признаку

Классификация моделей по временнопространственному признаку
• Классификация процессов:
- процессы неизменные во времени (стационарные);
- процессы переменные во времени (нестационарные);
- процессы с неизменными в пространстве параметрами;
- процессы с изменяющимися в пространстве параметрами.
• Классификация моделей:
- модели, неизменные во времени - статические модели;
- модели, переменные во времени - динамические модели;
- модели, с неизменными в пространстве параметрами - модели с
сосредоточенными параметрами;
- модели, с изменяющимися в пространстве параметрами - модели
с распределенными параметрами.

6.

V , C A0 , C B0
Статическая модель
V (CA CA ) VkCA CB , V (CB CB ) VkCA CB .
0
0
Динамическая модель
V
V , C A , C B
dCA
V (CA CA ) VkCA CB ,
dt
0
V
dCB
V (CB CB ) VkCA CB
dt
0

7. Модель с распределенными параметрами

dz
C вхWF
C
dz WF
C
z
CWF
L
C выхWF

8. Основные принципы и направления при построении и решении математических моделей

Составление модели.
- Аналитический метод
- Экспериментальный
- Экспериментально-аналитический
Нахождение решения модели.
Проверка модели на адекватность.
Аналитический метод - вывод уравнений осуществляется на основании
теоретического анализа физических и химических закономерностей
протекания процесса, конструктивных параметров аппаратуры и свойств
перерабатываемых веществ.
При выводе используются фундаментальные законы сохранения вещества
и энергии, кинетические закономерности протекания химических
процессов, процессов тепло- массопереноса и других.
Аналитический метод используется для составления моделей только
хорошо изученных процессов и не требует проведения экспериментов.
Недостаток – сложность решения полученных уравнений в случае
сравнительно полного описания объекта.

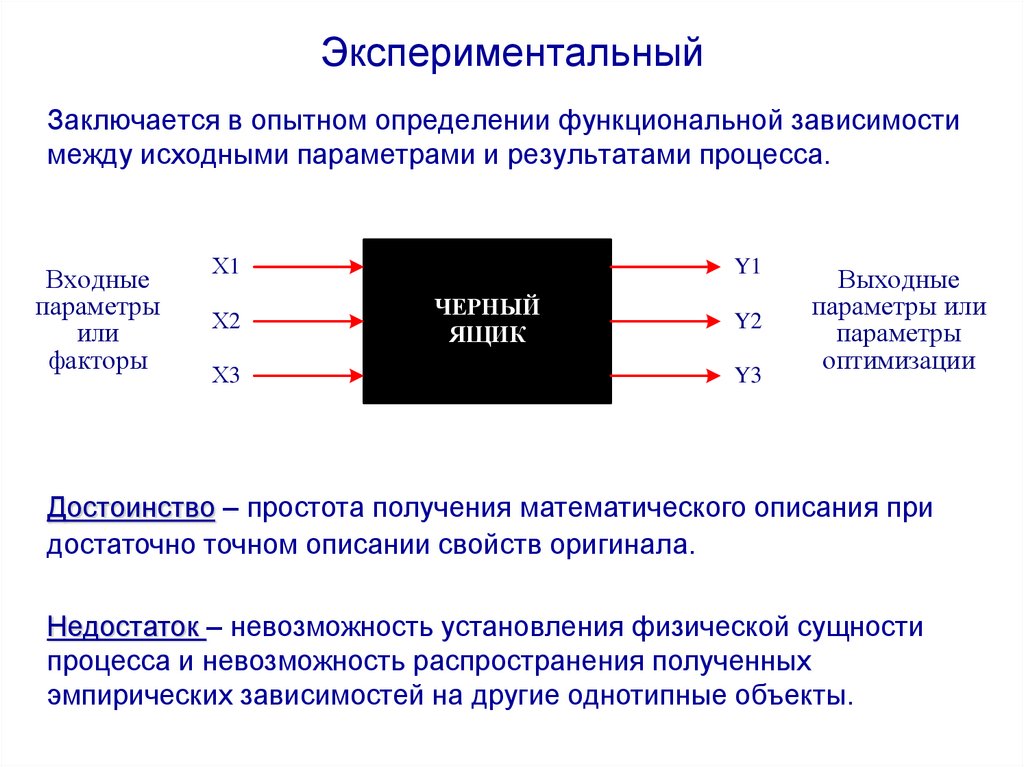
9. Экспериментальный

Заключается в опытном определении функциональной зависимости
между исходными параметрами и результатами процесса.
Входные
параметры
или
факторы
Х1
Х2
Х3
Y1
ЧЕРНЫЙ
ЯЩИК
Y2
Y3
Выходные
параметры или
параметры
оптимизации
Достоинство – простота получения математического описания при
достаточно точном описании свойств оригинала.
Недостаток – невозможность установления физической сущности
процесса и невозможность распространения полученных
эмпирических зависимостей на другие однотипные объекты.

10. Пример создания математической модели экспериментальным методом

H H (G )
Температура хладоагента, о С
100
0,05
80
0,04
60
0,03
T T (G )
40
0,02
20
0,01
0
0
1
2
3
4
5
6
7
8
9
10
11
Расход теплоносителя, G
Температура хладоагента Т
Гидравлическое сопротивление Н
Гидравлическое сопротивление теплообменника, МПа
Пример создания математической модели экспериментальным методом

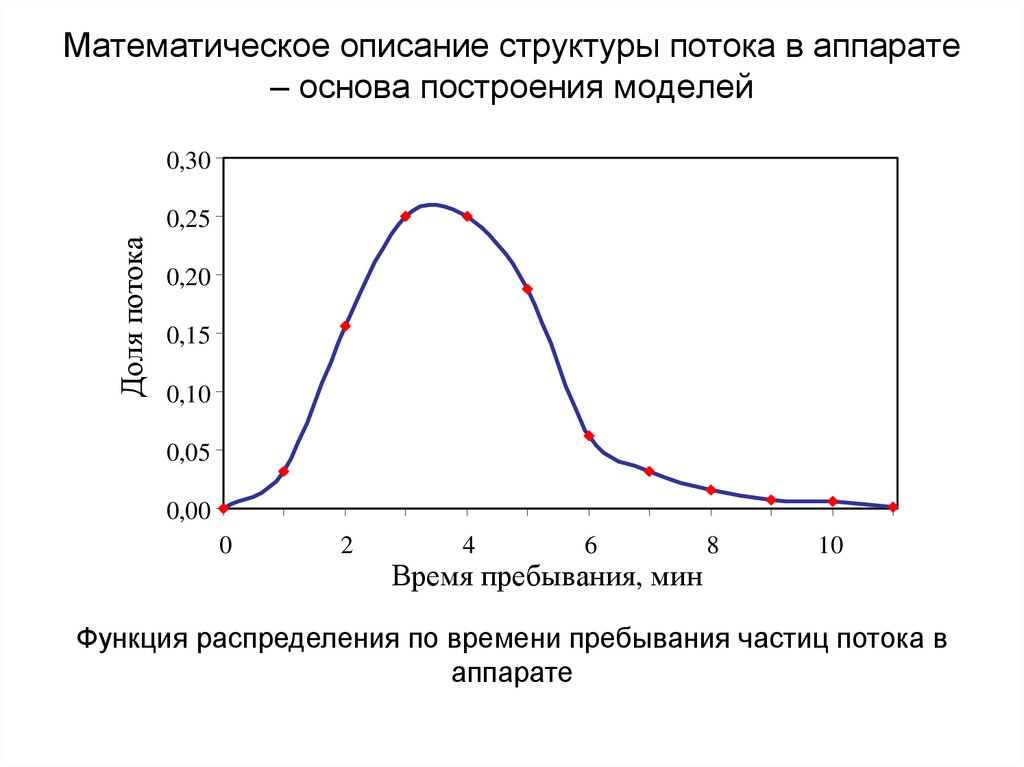
11. Математическое описание структуры потока в аппарате – основа построения моделей

0,30
Доля потока
0,25
0,20
0,15
0,10
0,05
0,00
0
2
4
6
Время пребывания, мин
8
10
Функция распределения по времени пребывания частиц потока в
аппарате

12. Методы исследования структуры потоков

Требования к индикатору:
- поведение в аппарате подобно поведению частиц потока;
- отсутствие взаимодействия со средой;
- легко измеряться.
Импульсный метод
8
6
4
отклик
возмущение
Концентрация, мг/л
10
2
0
0
2
4
6
8
Время измерения, мин
10

13. Ступенчатый

Концентрация, мг/л
Ступенчатый
40
35
30
25
20
15
10
5
0
возмущение
отклик
0
2
4
6
8
Время измерения, мин
10

14. Типовые модели структуры потока

Требования к моделям:
• отражение физической сущности реального потока при
достаточно простом математическом описании;
• простота определения параметров экспериментальным
или расчетным путем;
• удобство для использования при расчетах конкретных
химико-технологических процессов.
Классы моделей: идеальные и реальные.
• Идеальные: ИП и ИВ. Предполагают идеальную
структуру потока и не всегда адекватны реальным
процессам.
• Реальные: ЯМ; ЯМР и ДМ.

15. Модель идеального перемешивания

скачок
Свх
Cвх ,V
V
dC
V (Cвх C )
dt
С = Свых
dC Cвх C
dt
t
t V / V - среднее время пребывания потока в аппарате.
35
30
25
20
15
10
5
(Cвых С ),V
отклик
отклик
возмущение
35
Концентрация, мг/л
C
ступенчатое
40
возмущение
Концентрация, мг/л
импульсное
40
30
25
20
15
10
5
0
0
0
2
4
6
t, мин
8
10
0
2
4
6
t, мин
8
10

16. Модель идеального вытеснения

dz
W, C
V, Свх
W , (C +
C
z
dz )
V, Свых
C
C
dz WF
CWF C
z
t
Концентрация, мг/л
Fdz
Fdz
C
C
C
C
W
dzWF
CWF СWF
z
t
z
t
Концентрация, мг/л
l
40
35
30
25
20
15
10
5
0
импульсное
40
35
30
25
20
15
10
5
0
возмущение
отклик
t 8
0
10
8
6
4
2
Время измерения, мин
ступенчатое
возмущение
отклик
t 8
0
8
6
4
2
Время измерения, мин
10

17. Ячеечная модель

Cвх ,V вх
C1
C2
Ci
C1 ,V 1
dC1 Cвх С1
dt
t
Cn
C 2 ,V 2
Ci ,V i
C n , V n
dCi Ci 1 Сi
dt
t
dCn Cn 1 Сn
dt
t
6
4
отклик
Концентрация, мг/л
8
возмущение
Концентрация, мг/л
10
2
0
0
2
4
6
8
Время измерения, мин
10
40
35
30
25
20
15
10
5
0
возмущение
отклик
0
2
4
6
8
Время измерения, мин
10

18. Ячеечная модель с рециркуляцией

Cвх ,V
V
C1
V
dC1
VCвх vC2 V v С1
dt
dCi
V v Ci 1 vCi 1 V 2v Сi
dt
C2
C1 , (V )
C2 ,
V
Ci
Cn
C 2 , (V )
Ci , (V )
Ci ,
Cn ,
6
4
Концентрация, мг/л
8
возмущение
Концентрация, мг/л
10
отклик
2
0
0
2
4
6
8
Время измерения, мин
10
dCn
V v Cn 1 V v Cn
dt
40
35
30
25
20
15
10
5
0
f
f v / V
t
возмущение
t
отклик
2
4
6
8
Время измерения, мин
10
dC 1
C вх fC 2 1 f С 1
dt
dCi
1 f Ci 1 fCi 1 1 2 f Сi
dt
t
0
t V / V
dC n
1 f C n 1 1 f Cn
dt

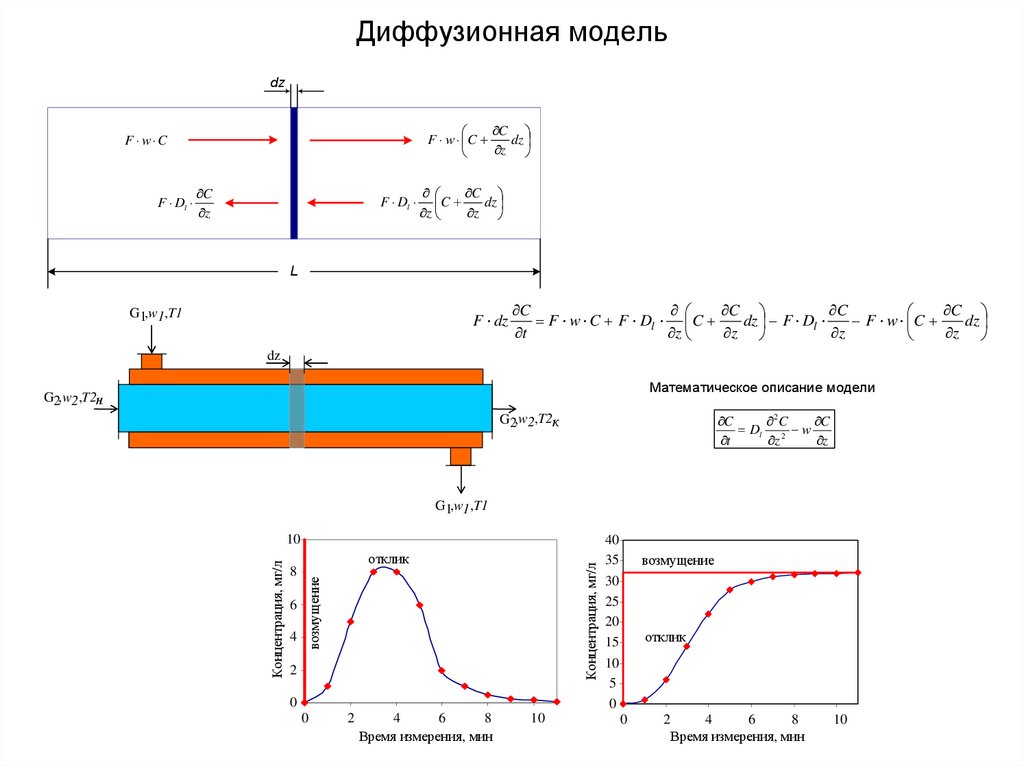
19. Диффузионная модель

dz
C
F w C
dz
z
F w C
F Dl
C
z
F Dl
C
dz
C
z
z
L
G1,w1,T1
F dz
C
C
C
C
F w C F Dl C
dz F Dl
F w C
dz
t
z
z
z
z
dz
Математическое описание модели
G2,w2,T2н
C
2C
C
Dl 2 w
t
z
z
G2,w2,T2к
G1,w1,T1
6
4
отклик
Концентрация, мг/л
8
возмущение
Концентрация, мг/л
10
2
0
0
2
4
6
8
Время измерения, мин
10
40
35
возмущение
30
25
20
15
отклик
10
5
0
0
2
4
6
8
Время измерения, мин
10