Стереометрия. Поурочное планирование (10 -11 класс)

1. Стереометрия

по учебнику для 10-11 классов
средней школы
Авторы Л. С. Атанасян, В. Ф. Бутузов и др.

2. Поурочное планирование

1.
2.
3.
4.
5.
6.
Предмет и аксиомы стереометрии.
Следствия из аксиом.
Решение задач на построение.
Решение задач на построение
Решение задач на построение.
Практическая работа.

3. Предмет и аксиомы стереометрии.

СТЕРЕОМЕТРИЯ – это раздел
геометрии, в котором
изучаются свойства фигур в
пространстве.
Слово «стереометрия»
происходит от греческих слов
«стереос» - объёмный,
пространственный и
«метрео» - измерять.
Первый дошедший до нас учебник – руководство по
математике под названием «Начала», созданное
древнегреческим ученым Евклидом в III в. до н. э. В
течение длительного времени геометрию изучали по
этой книге.

4. Неопределяемые понятия и отношения

Формулировки Евклида:
• Точка есть то, что не имеет частей.
• Прямая есть длина без ширины.
• Плоскость есть то, что имеет только длину и ширину.
Современная концепция:
Точка
Прямая
Поверхность
Принадлежность
Между
Конгруэнтность

5. Простейшие геометрические тела.

Геометрическое тело – это предмет, от которого
отняты все его свойства, кроме пространственных.

6. Геометрические фигуры

Геометрические тела, как и другие
геометрические фигуры, являются
воображаемыми объектами.
Изучая свойства геометрических
пространственных фигур мы получаем
представление о геометрических
свойствах реальных предметов.

7. Условные изображения пространственных фигур.

Условное
изображение
пространственной
фигуры – это её
проекция на
плоскость.
Обычно выбирают то
изображение,
которое создаёт
правильное
представление о
форме фигуры.

8. Условные обозначения

• Точки - прописными латинскими
буквами (A, B, C, D, E, F, G, H, ...)
• Прямые – строчными латинскими
буквами (a, b, c, d, e, f, g, h, ...)
• Плоскости – строчными греческими
буквами (a, b, g, d, e, z, h, q, i, k, l, m, n, x,
o, p, r, s, t, u, f, c, y, w)

9. Греческий алфавит

A a - альфа
B b - бета
G g - гамма
d - дельта
e - эпсилон
Z z - дзета
H h - каппа
Q q - тэта
I i – йота
K k – каппа
M m – мю
L l - лямбда
N n - ню
X x - кси
O o - омикрон
P p - пи
R r - ро
S s - сигма
T t - тау
U u - ипсилон
F f - фи
C c - хи
Y y - пси
W w - омега

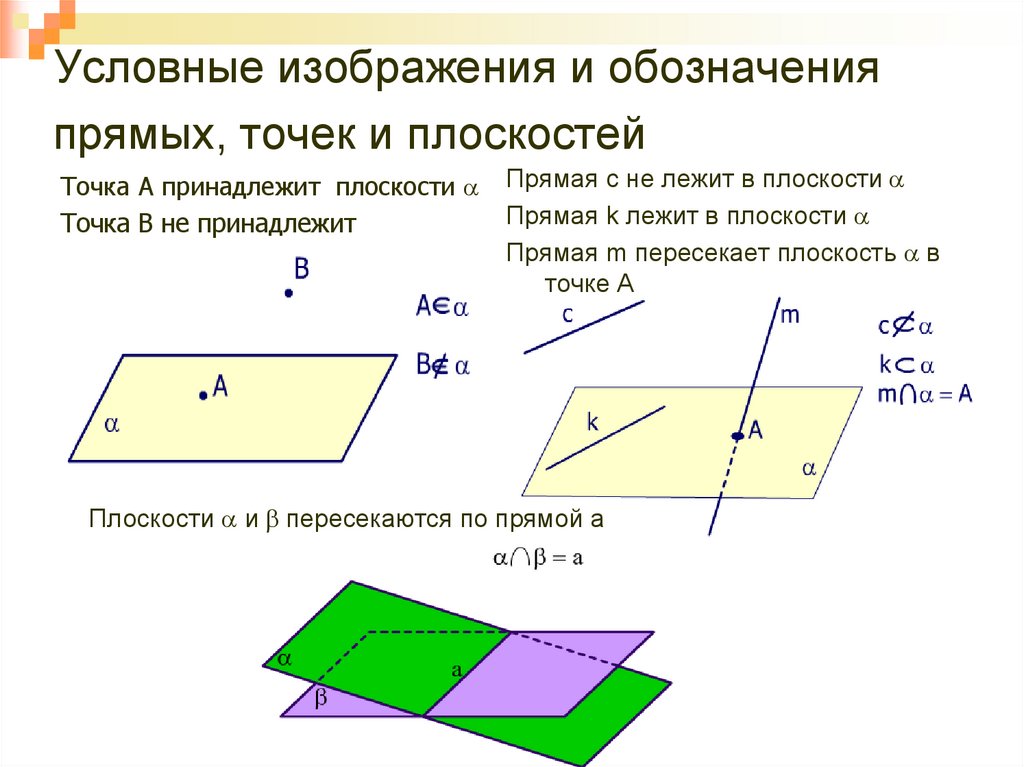
10. Условные изображения и обозначения прямых, точек и плоскостей

Точка А принадлежит плоскости a
Точка В не принадлежит
плоскостиa
Прямая с не лежит в плоскости a
Прямая k лежит в плоскости a
Прямая m пересекает плоскость a в
точке А
Плоскости a и b пересекаются по прямой а

11. Что такое аксиома?

АКСИОМА – это высказывание,
истинность которого принимается без
доказательства (аксиома - греческое
слово, означающее «бесспорное
положение»).
Аксиомы были сформулированы
Евклидом ( III в. До н. э.) в его
знаменитом сочинении «Начала».

12. Вспомним известные вам аксиом планиметрии:

Каждой прямой принадлежат по крайней
мере две точки.
Из трех точек прямой одна и только одна
лежит между двумя другими.
Через любые две точки можно провести
прямую, и притом только одну.
Через точку, не лежащую на данной прямой,
проходит только одна прямая,
параллельная данной.
Если две фигуры совмещаются наложением,
то говорят, что они равны.

13. А1: Через любые три точки, не лежащие на одной прямой проходит плоскость, и притом только одна.

ВОПРОСЫ:
-всегда ли три точки лежат в одной плоскости?
-всегда ли четыре точки лежат в одной плоскости?
-всегда ли через три точки проходит плоскость, и притом только
одна?
-сколько плоскостей можно провести через две точки?

14. А2: Если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости.

ВОПРОСЫ: верно ли утверждение:
-если две точки окружности лежат в плоскости, то и вся окружность
лежит в этой плоскости?
-если три точки окружности лежат в в этой плоскости?
-если прямая пересекает две стороны треугольника, то она лежит в
плоскости данного треугольника?

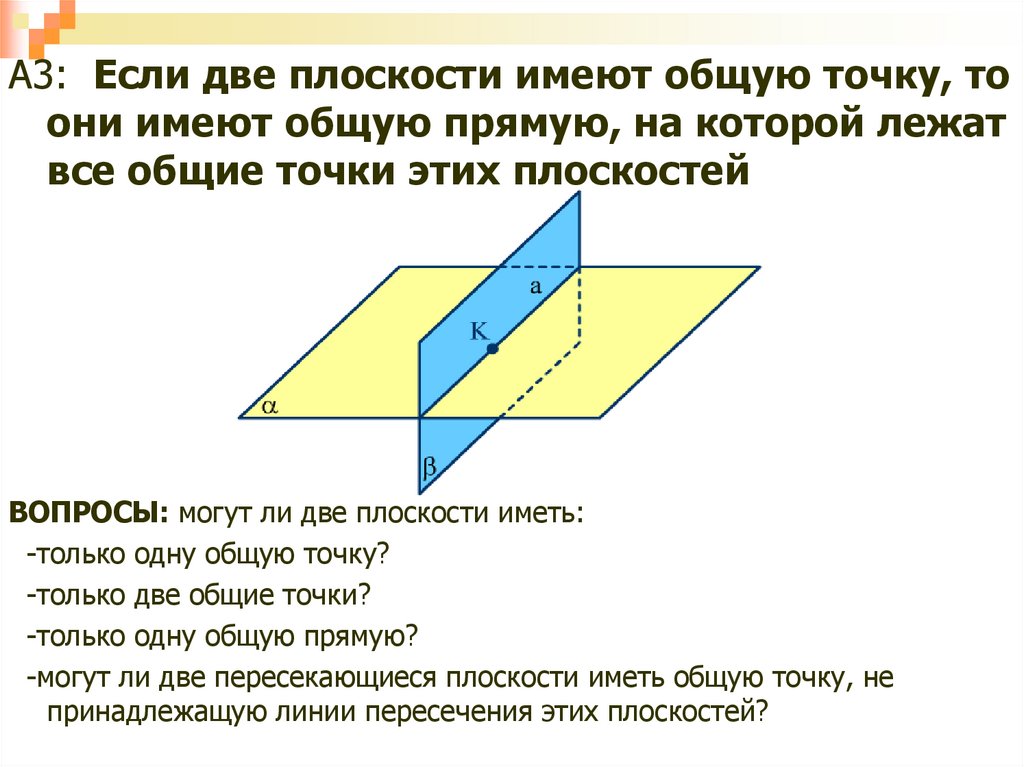
15.

А3: Если две плоскости имеют общую точку, то
они имеют общую прямую, на которой лежат
все общие точки этих плоскостей
ВОПРОСЫ: могут ли две плоскости иметь:
-только одну общую точку?
-только две общие точки?
-только одну общую прямую?
-могут ли две пересекающиеся плоскости иметь общую точку, не
принадлежащую линии пересечения этих плоскостей?

16.

Рассмотрим куб ABCDА1B1C1D1
ВОПРОСЫ:
а) назовите точки, которые лежат в плоскости DCC1, ABC, ADD1;
б) назовите плоскости, которым принадлежат точки М, К, P1, R, S, N;
в) назовите плоскости , в которых расположены прямые KP, С1D1, RP, MK;
г) назовите прямые, по которым пересекаются плоскости ABC и DD1C1,
BB1C1 и AA1B1, AA1D1 и A1B1C1;

17.

Рассмотрим куб ABCDА1B1C1D1
ВОПРОСЫ:
д) назовите прямые, по которым пересекаются плоскости ABC и KPN,
RPK и DСС1, BDC1 ;
е) назовите точки пересечения прямых DS и CC1, AD и PC, MR и AD,
KP и AD, DC1 и RP1;
ж) назовите общие точки плоскостей CDD1 и BCC1, ABC и АА1D1, BDC и
ABB1.BDС1 и RSP;

18. Проверим выполнение задания.

а) R DCC1, P DCC1, S DCC1,
К ABC, K1 ABC, P ABC, P1 ABC,
M ADD1, R ADD1, K ADD1, P1 ADD1;
б) M ABB1, M ADD1, K1 ABC, K ABB1, P1 ABC, P1 DCC1, R
ADD1, R DCC1, S DCC1, N A1B1C1, N BCC1;
в) KP ABC, C1D1 CDD1, C1D1 A1B1C1, RP CDD1, MK AA1B1;
г) ABC ∩ DD1C1=DC, BB1C1 ∩ AA1B1=BB1, AA1D1 ∩ A1B1C1=A1D1;
д) ABC ∩ KPN = KP, RPK ∩ DCC1 = RP, BDC1 ∩ RSP = DC1;
е) DS ∩ CC1=C1, AD ∩ PC=D, MR ∩ AD=P1, KP ∩ AD=K1, DC1∩ RP1= ;
ж) C,C1 (CDD1∩BCC1), A1,D1,K1, P1 (ABC∩AA1D1), A,K,B
(BDC∩ABB1).
ДОМАШНЕЕ ЗАДАНИЕ: устно п. 1-2, письменно № 1 (перечертить чертеж
и ответ записать с помощью символики), № 11.