2.86M

Категории:

Информатика

Программное обеспечение

Похожие презентации:

Работа в Excel 2007

Работа в Excel 2007 (1-6)

Работа в Excel 2007

Работа в Excel

Работа в Excel 2007

Решение вычислительных задач на компьютере

Работа в Excel 2007

1. Работа в Excel 2007

1
Работа в Excel 2007
1.
2.
3.
4.
5.
6.
Основы
Диаграммы
Численные методы
Статистика
Восстановление зависимостей
Моделирование
© К.Ю. Поляков, 2009-2012

2. Работа в Excel 2007

2
Работа в Excel 2007
Тема 1. Основы
© К.Ю. Поляков, 2009-2012

3.

Электронные таблицы
Основная задача – автоматические вычисления с
данными в таблицах.
Кроме того:
• хранение данных в табличном виде
• представление данных в виде диаграмм
• анализ данных
• составление прогнозов
• поиск оптимальных решений
• подготовка и печать отчетов
Примеры:
• Microsoft Excel – файлы *.xls, *.xlsx
• OpenOffice Calc – файлы *.ods – бесплатно
3

4.

4
Электронные таблицы
имена столбцов
активная
ячейка
номера
строк
неактивная
ячейка
строка
текст
числа
формулы
время
дата
столбец

5.

5
Начало работы с Microsoft Excel
Программы – Microsoft Office – Excel 2007
Файлы:
*.xlsx (старая версия – *.xls)
Вася.xlsx рабочая книга
Лист 1
переходы
по листам
Лист 2
План
по валу
Вал
по плану
ЛКМ
ПКМ
новый лист

6.

6
Адреса
адрес активной ячейки
диапазон B2:С7
B2
ячейка B2
Ссылки в формулах:
=B2+2*C3
=A2+2*СУММ(B2:C7)
!
Формула всегда начинается знаком «=»!
С7

7.

7
Ввод данных
адрес
активной
ячейки
отменить (Esc)
принять (Enter)
строка
редактирования
ЛКМ
F2 – редактировать прямо в ячейке

8.

8
Выделение данных
ячейка:
ЛКМ
диапазон:
+ЛКМ
– ЛКМ
строки:
ЛКМ
несвязанные диапазоны:
+Ctrl и выделять второй
столбцы:
ЛКМ
вся таблица:
ЛКМ

9.

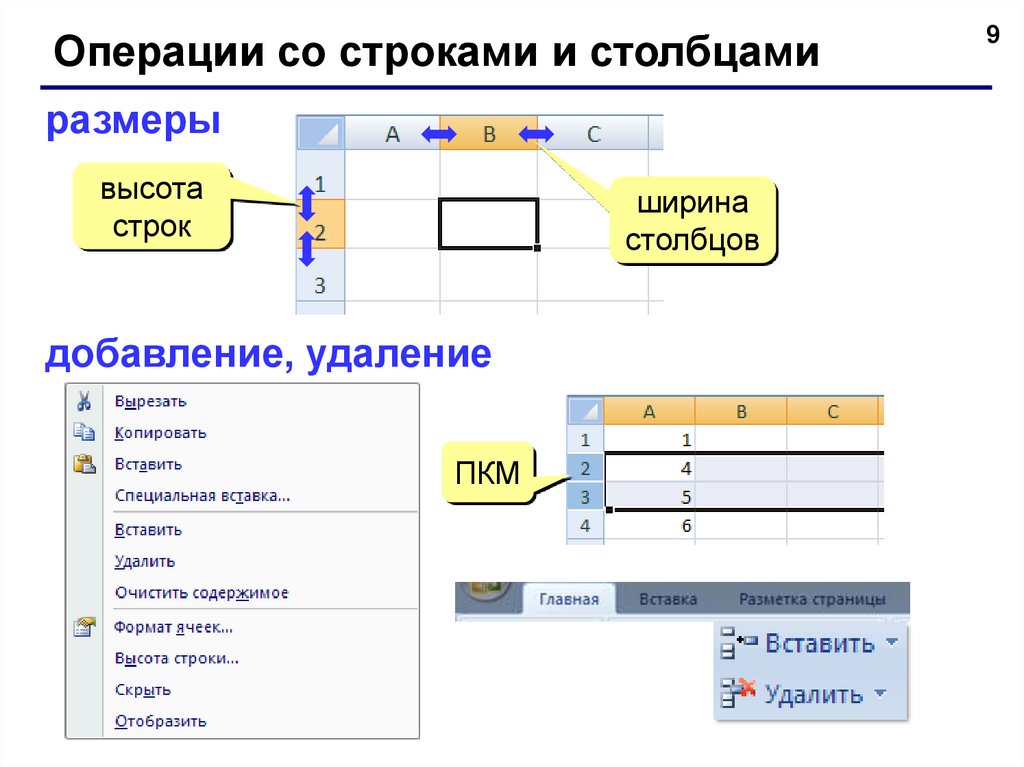
Операции со строками и столбцами
размеры
высота
строк
ширина
столбцов
добавление, удаление
ПКМ
9

10.

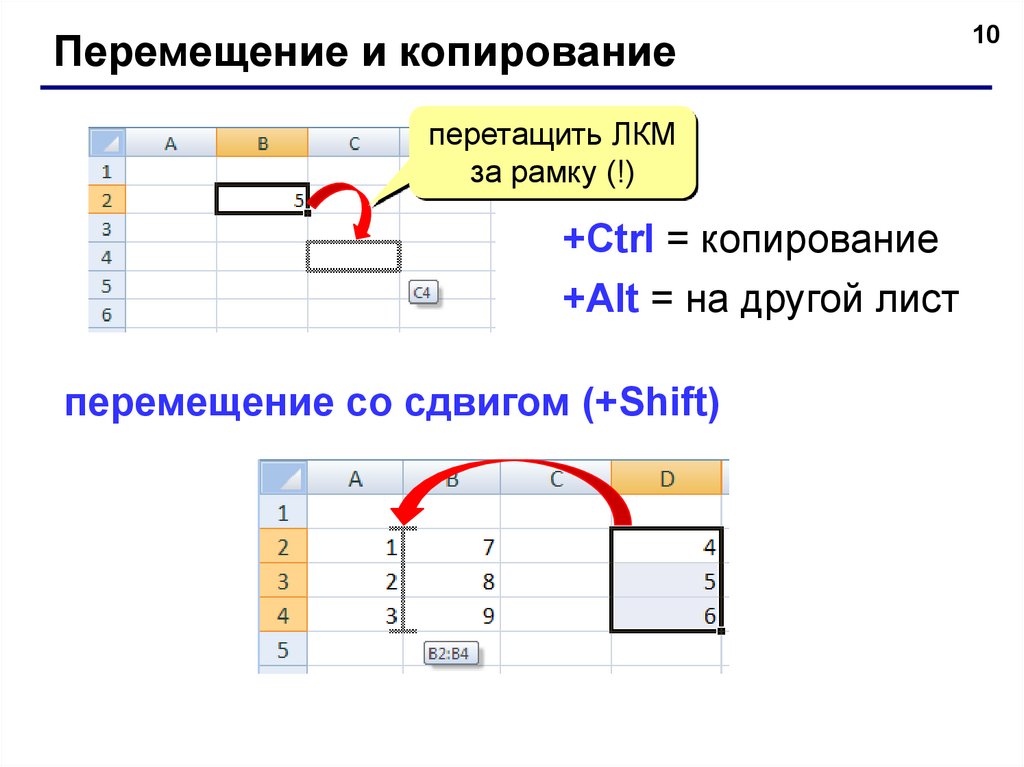
Перемещение и копирование
перетащить ЛКМ
за рамку (!)
+Ctrl = копирование
+Alt = на другой лист
перемещение со сдвигом (+Shift)
10

11.

11
Типы ссылок
относительные
(меняются так же, как и адрес формулы )
формула «переехала»
на один столбец вправо
и на одну строку вниз;
имя столбца на 1
номер строки на 1
абсолютные
смешанные
(не меняются)
(меняется только относительная часть)

12.

12
Заполнение рядов
арифметическая прогрессия
копирование формул
маркер
заполнения
ЛКМ
даты
ЛКМ
время
списки

13.

13
Оформление ячеек
размер
все свойства
направление
в несколько
строк
денежный
формат
количество знаков
в дробной части

14.

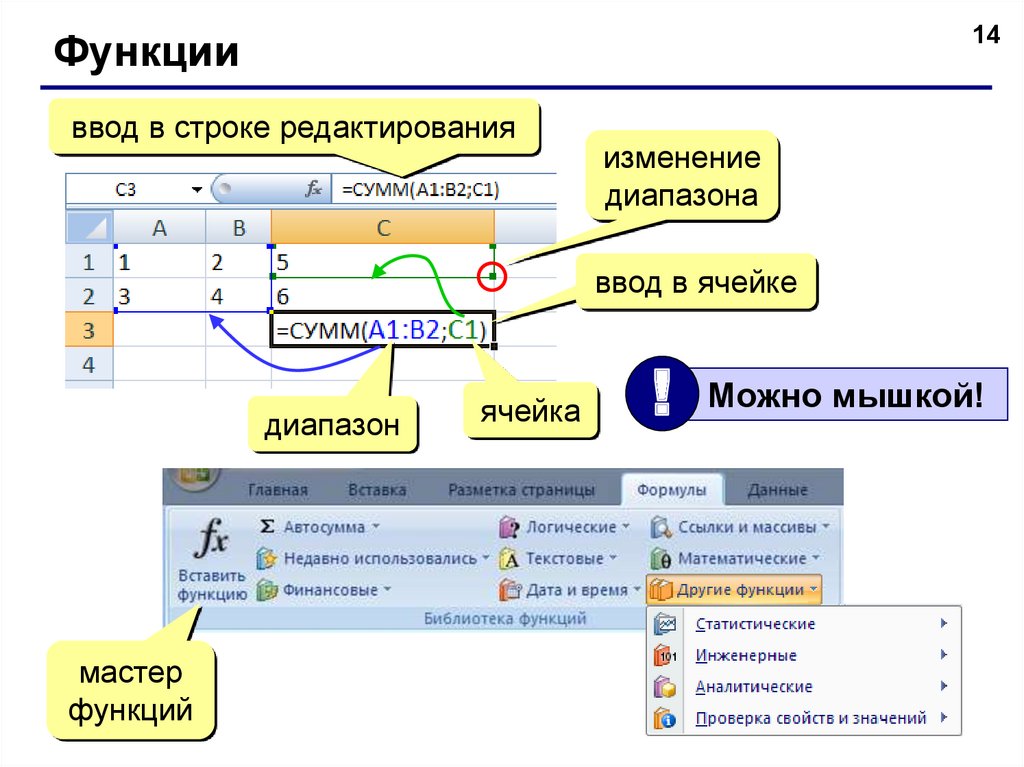
14
Функции
ввод в строке редактирования
изменение
диапазона
ввод в ячейке
диапазон
мастер
функций
ячейка
!
Можно мышкой!

15. Некоторые функции

Электронные таблицы
15
Некоторые функции
СУММ – сумма значений ячеек и диапазонов
СРЗНАЧ – среднее арифметическое числовых ячеек
МИН – минимальное значение
МАКС – максимальное значение
!
Пустые и нечисловые ячейки не учитываются!
К. Поляков, 2011-2014
http://kpolyakov.narod.ru

16. Некоторые функции

Электронные таблицы
16
Некоторые функции
Сумма значений нескольких диапазонов
(СУММ, СРЗНАЧ, МИН, МАКС)
К. Поляков, 2011-2014
http://kpolyakov.narod.ru

17. Некоторые функции

Электронные таблицы
17
Некоторые функции
СУММПРОИЗВ – сумма произведений двух массивов
К. Поляков, 2011-2014
http://kpolyakov.narod.ru

18. Некоторые функции

Электронные таблицы
18
Некоторые функции
СЧЁТ – количество числовых ячеек
СЧЁТЕСЛИ – количество ячеек, удовлетворяющих
заданному условию (2-ой параметр)
К. Поляков, 2011-2014
http://kpolyakov.narod.ru

19. Некоторые функции

Электронные таблицы
19
Некоторые функции
СУММЕСЛИ – сумма ячеек диапазона, удовлетворяющих
условию, которое накладывается на другой диапазон
Найти общий вес учащихся 9-А класса.
диапазон для
проверки
условия
условие
диапазон для
суммирования
К. Поляков, 2011-2014
http://kpolyakov.narod.ru

20.

20
Функция ЕСЛИ
ЕСЛИ – выбор из двух вариантов
условие
если «да»
если «нет»
=ЕСЛИ(B2="сдал";
ЕСЛИ(A2>80;
5; 4); "–")
=ЕСЛИ(A2>=70;
"сдал";
"не сдал")

21.

Логические операции
НЕ – обратное условие, НЕ(B2<10)
?B2>=10
И – одновременное выполнение всех условий
=ЕСЛИ( И(B2>1994; C2>175);"да";"–")
21

22.

Логические операции
22
ИЛИ – выполнение хотя бы одного из условий
=ЕСЛИ( ИЛИ(B2=100; C2=100; B2+C2>=180);"да";"–")

23.

Подсчёт числовых значений
СЧЁТ – считает ячейки с числами или формулами,
которые дают числа
=A1+1
2
23

24.

24
Подсчёт значений по условию
СЧЁТЕСЛИ – считает ячейки, удовлетворяющие условию
2
3
2
1

25.

Сортировка
Сортировка – это расстановка
элементов в заданном порядке.
Сортировка одного столбца
25

26.

26
Сортировка связанных данных
?
критерий
Почему нельзя
сортировать по
столбцу?
строки или
столбцы
первая
строка – это
заголовки

27.

Многоуровневая сортировка
Задача: расставить фамилии по
алфавиту, а людей с одинаковыми
фамилиями расставить в
алфавитном порядке по именам.
ЛКМ
27

28.

Имена ячеек и диапазонов
Присвоить имя
ввести имя
Работа с именами
Имена в формулах
28

29. Работа в Excel 2007

30.

Общий подход
• диаграммы строятся на основе данных
таблицы
• проще всего сначала выделить все нужные
данные, а потом…
• все данные, которые должны обновляться
автоматически, нужно выделить
• для выделения несвязанных диапазонов
используем +Ctrl
30

31.

Основные типы диаграмм
Гистограмма (столбчатая диаграмма):
сравнение значений одного или
нескольких рядов данных
График: показывает изменение
процесса во времени
(равномерные отсчеты)
31
Круговая: доли в сумме
Точечная: связь между
парами значений (график функции)

32.

32
Элементы диаграмм
название
диаграммы
сетка
подписи
данных
легенда
ряды
данных
ось
названия осей

33.

Настройка диаграммы и ее элементов
Конструктор: общие свойства
Макет: настройка свойств отдельных элементов
Формат: оформление отдельных элементов
33

34.

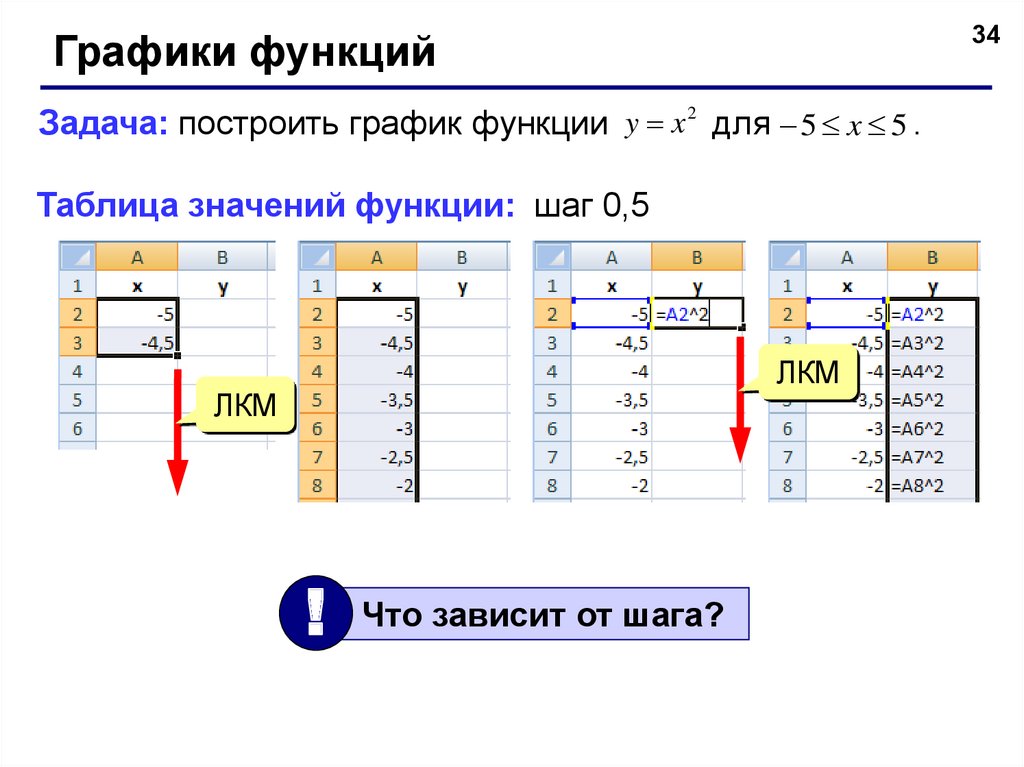
34
Графики функций
Задача: построить график функции y x 2 для 5 x 5 .
Таблица значений функции: шаг 0,5
ЛКМ
ЛКМ
!
Что зависит от шага?

35.

Графики функций
Вставка диаграммы «Точечная»:
выделить данные
результат:
35

36. Работа в Excel 2007

37.

Решение уравнений
37
Задача: найти все решения уравнения x 2 5 cos x
на интервале [-5,5]
?
Как решить математическими методами?
Методы решения уравнений:
• аналитические: решение в виде формулы x ...
• численные: приближенное решение, число
1) выбрать начальное приближение x0 «рядом» с
решением
?
Как выбрать начальное приближение?
2) по некоторому алгоритму вычисляют первое
приближение, затем – второе и т.д. x0 x1 x2 ...
3) вычисления прекращают, когда значение меняется очень
*
мало (метод сходится) x0 ... x15 x16 x

38.

Решение уравнения x 5 cos x
38
2
1. Таблица значений функций на интервале [-5,5]
2. Графики функций (диаграмма «Точечная»)
2 решения:
начальные приближения
x0 1,5
x0 1,5

39.

Решение уравнения x 5 cos x
39
2
3. Подготовка данных
начальное
приближение
целевая
ячейка
Цель: H2=0
?
Зачем нужна разность?

40.

Решение уравнения x 5 cos x
40
2
4. Подбор параметра
ошибка
решение
уравнения
?
?
Как найти второе решение?
Почему
не нуль?

41.

41
Оптимизация
Оптимизация – это поиск оптимального (наилучшего)
варианта в заданных условиях.
Оптимальное решение – такое, при котором некоторая
заданная функция (целевая функция) достигает
минимума или максимума.
Постановка задачи:
• целевая функция
(расходы, потери, ошибки)
f ( x) min
f ( x) max
(доходы, приобретения)
• ограничения, которые делают задачу осмысленной
Задача без ограничений: построить дом
при минимальных затратах.
Решение: не строить дом вообще.

42.

42
Оптимизация
f (x)
локальный
минимум
глобальный
минимум
x
• обычно нужно найти глобальный минимум
• большинство численных методов находят только
локальный минимум
• минимум, который найдет Excel, зависит от выбора
начального приближения («шарик на горке скатится в
ближайшую ямку»)

43.

43
Поиск минимума функции
y x 2 6 sin x 5 cos x
1. Строим график функции (диаграмма «Точечная»)
?
Зачем нужен
график?
начальное приближение
x0 2
2. Подготовка данных
начальное
приближение
!
целевая
ячейка
Изменение E2 должно влиять на F2!

44.

44
Поиск минимума функции
3. Надстройка «Поиск решения»
изменяемые
ячейки:
E2
D2:D6
D2:D6; C5:C8
ограничения
A1 <= 20
B2:B8 >= 5
A1 = целое
целевая
ячейка

45.

Параметры оптимизации
45

46.

Оптимизация
?
Подбор параметра – это оптимизация?
Надстройка «Поиск решения» позволяет:
• искать минимум и максимум функции
• использовать несколько изменяемых ячеек и
диапазонов
• вводить ограничения (<=, >=, целое, двоичное)
?
Как влияет ограничение «A1-целое» на
сложность решения задачи?
46

47. Работа в Excel 2007

48.

Ряд данных и его свойства
48
Ряд данных – это упорядоченный набор значений
x1 , x2 , ..., xn
Основные свойства (ряд A1:A20):
• количество элементов =СЧЕТ(A1:A20)
• количество элементов, удовлетворяющих
некоторому условию:
= СЧЕТЕСЛИ(A1:A20;"<5")
• минимальное значение =МИН(A1:A20)
• максимальное значение =МАКС(A1:A20)
• сумма элементов =СУММ(A1:A20)
• среднее значение =СРЗНАЧ(A1:A20)

49.

49
Дисперсия
Для этих рядов одинаковы МИН, МАКС, СРЗНАЧ
?
В чем различие?
Дисперсия («разброс») – это величина, которая
характеризует разброс данных относительно
среднего значения.

50.

50
Дисперсия
n
2
(
x
x
)
i
( x1 x ) 2 ( x2 x ) 2 ( xn x ) 2 i 1
Dx
n
n
x1 x2 xn
x
среднее арифметическое
n
( x1 x )
2
квадрат
отклонения x1
от среднего
Dx средний квадрат
отклонения от
среднего значения

51.

51
Дисперсия и СКВО
Стандартная функция
=ДИСПР(A1:A20)
Функции – Другие – Статистические
Что неудобно:
если x измеряется в метрах,
то Dx – в м2
?
В каких
единицах
измеряется?
СКВО = среднеквадратическое отклонение
x Dx
=СТАНДОТКЛОНП(A1:A20)

52.

Взаимосвязь рядов данных
Два ряда одинаковой длины:
x1 , x2 , ..., xn
y1 , y2 , ..., yn
Вопросы:
• есть ли связь между этими рядами (соответствуют
ли пары ( xi , yi ) какой-нибудь зависимости y f (x) )
• насколько сильна эта связь?
52

53.

53
Взаимосвязь рядов данных
Ковариация:
n
K xy
?
Если x и
x
i 1
i
x y i y
n
y – один и тот же ряд?
K xx Dx
в среднем!
Как понимать это число?
• если K xy 0 увеличение x приводит к увеличению y
• если K xy 0 увеличение x приводит к уменьшению y
• если K xy 0 связь обнаружить не удалось
Что плохо?
• единицы измерения: если x в метрах, y в литрах,
то K xy – в м л
• K xy зависит от абсолютных значений x и y , поэтому
ничего не говорит о том, насколько сильна связь

54.

54
Взаимосвязь рядов данных
Коэффициент корреляции:
xy
?
K xy
x y
x, y
Какова размерность?
– СКВО рядов
x
и
y
безразмерный!
1 xy 1
Как понимать это число?
• если xy 0 : увеличение x приводит к увеличению y
• если xy 0 : увеличение x приводит к уменьшению y
• если xy 0 : связь обнаружить не удалось
=КОРРЕЛ(A1:A20;B1:B20)

55.

Взаимосвязь рядов данных
55
Как понимать коэффициент корреляции?
0 xy 0,2 : очень слабая корреляция
0,2 xy 0,5 : слабая
0,5 xy 0,7 : средняя
0,7 xy 0,9 : сильная
0,9 xy 1 : очень сильная
xy 1 : линейная зависимость y ax b, a 0
xy 1 : линейная зависимость y ax b, a 0
?
Если xy 0 , то связи нет?
!
Метод для определения линейной зависимости!

56. Работа в Excel 2007

57.

Восстановление зависимостей
57
Два ряда одинаковой длины:
x1 , x2 , ..., xn
y1 , y2 , ..., yn
задают некоторую неизвестную функцию y f (x)
Зачем:
• найти y в промежуточных точках
(интерполяция)
y f (x)
y2
y1
x1 x2
xn
• найти y вне диапазона
измерений
(экстраполяция,
прогнозирование)

58.

Какое решение нам нужно?
y f 2 ( x)
y f1 ( x)
y2
y1
x1 x2
!
xn
Через заданный набор точек проходит
бесконечно много разных кривых!
Вывод: задача некорректна, поскольку решение
неединственно.
58

59.

59
Восстановление зависимостей
Корректная задача: найти функцию заданного вида,
которая лучше всего соответствует данным.
Примеры:
y f (x)
•линейная y a x b
y2
•полиномиальная
y1
y a3 x 3 a2 x 2 a1 x a0
•степенная y a x
•экспоненциальная
x1 x2
!
xn
График функции не
обязательно проходит
через заданные точки!
b
y a ebx
•логарифмическая
y a ln x b
?
Как выбрать
функцию?

60.

Что значит «лучше всего соответствует»?
Метод наименьших квадратов (МНК):
y f (x)
y2
y1
( xi , yi ) заданные пары
значений
Yi f ( xi )
Y1 Y2
n
( yi Yi ) 2 min
i 1
x1 x2
?
xn
Зачем возведение в квадрат?
1) чтобы складывать положительные значения
2) решение сводится к системе линейных
уравнений (просто решать!)
60

61. МНК для линейной функции

Электронные таблицы Excel
61
МНК для линейной функции
неизвестно!
y f (x)
y2
y1
Yi k xi
n
n
(k ) ( yi Yi ) ( yi kxi ) 2
2
i 1
Y1
n
n
k x k 2 xi yi yi2
Y2
2
i 1
xn
x1 x2
(k ) ak bk c min
k
k
i 1
i 1
-b
c
n
b
*
k
2a
*
2
i
a
2
К. Поляков, 2009-2012
i 1
n
x y
i 1
n
i
i
2
x
i
i 1
http://kpolyakov.narod.ru

62.

Коэффициент достоверности
n
R 1
2
(y Y )
i 1
n
i
2
i
2
(
y
y
)
i
i 1
( xi , yi ) заданные пары
значений
Yi f ( xi )
y – среднее значение yi
Крайние случаи:
• если график проходит через точки:
R 1
2
• если считаем, что y не меняется и
R2 0
!
Yi y:
Фактически – метод наименьших квадратов!
62

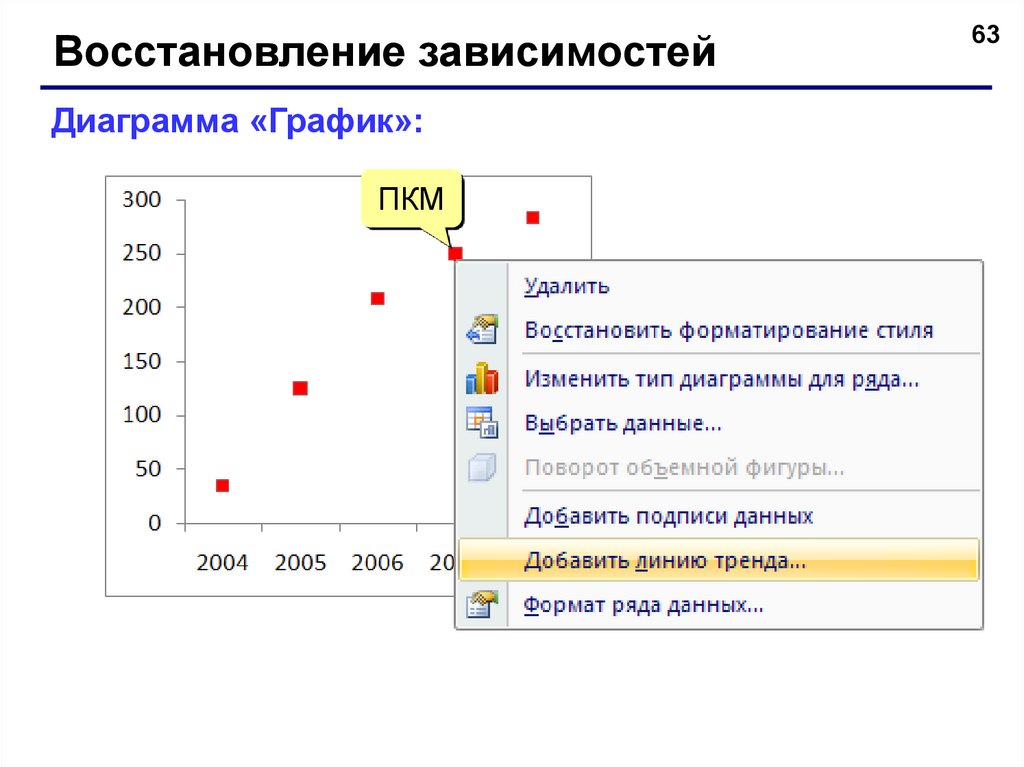
63.

Восстановление зависимостей
Диаграмма «График»:
ПКМ
63

64.

Восстановление зависимостей
тип
функции
64

65.

65
Восстановление зависимостей
?
!
?
Что такое
x?
В диаграмме «График»
x 1 для первой точки,
x 2 для второй и т.д.
Насколько хорошо выбрана функция?

66.

66
Восстановление зависимостей
Сложные случаи (нестандартная функция):
f ( x) a sin kx b
?
Что делать?
Алгоритм:
1) выделить ячейки для хранения a, k , b
2) построить ряд Yi f ( xi ) для тех же xi
3) построить на одной диаграмме ряды yi и Yi
4) попытаться подобрать a, k , b так, чтобы
два графика были близки
2
5) вычислить R в отдельной ячейке
функции: СУММКВРАЗН – сумма квадратов разностей рядов
ДИСПР – дисперсия
6) Поиск решения:
!
R min
2
Это задача оптимизации!

67. Работа в Excel 2007

68.

68
Модель деления
N
i
N 0 – начальная численность
N 2 N0
N1 2N 0 – после 1 цикла деления
N 2 2 N1 4 N 0 – после 2-х циклов
i
N0
N i 2 N i 1 2 N 0
Особенности модели:
1) не учитывается смертность
2) не учитывается влияние внешней среды
3) не учитывается влияние других видов
i

69.

69
Рождаемость и смертность
N i N i 1 K p N i 1 K c N i 1
Kp
Kc
– коэффициент рождаемости
– коэффициент смертности
N
N i K N i 1
Коэффициент изменения
численности
K 1 K p Kc
K 1
K 1
N0
K 1
Особенности модели:
1) не учитывается влияние численности N и внешней
среды на K
2) не учитывается влияние других видов на K
i