Функции нескольких переменных

1.

2.

Пусть имеется n переменных величин, и каждому
набору их значений
x1 , x2 ,...xn
из некоторого множества Х соответствует
определенное значение величины z.
Тогда говорят, что задана функция нескольких
переменных
z f ( x1 , x2 ,...xn )

3.

Функция
z x x2
2
1
задает объем цилиндра z как функцию двух
переменных:
х1 – радиус основания,
х2 – высота цилиндра.

4.

Переменные х1…хn называются независимыми
переменными.
Z называется зависимой переменной.
Множество Х называется областью
определения функции.

5.

1
Найти область определения функции:
z 1 x x
2
1
2
2

6.

1 x x 0
2
1
2
2
x x 1
2
1
2
2
Поэтому областью определения является круг с
центром в начале координат и радиусом,
равным единице.

7.

2
Найти область определения функции:
1
z
x1 x2

8.

x1 x2 0
x1 0
x2 0
Поэтому
областью
определения
является
плоскость
ОХ1Х2,
за
исключением
координатных прямых ОХ1 и ОХ2.

9.

Рассмотрим примеры
переменных.
функций
нескольких
1
z a1 x1 a2 x2 ... an xn b
a1 ,..., a2 , b const

10.

2
n
1
z bij xi x j
2 i , j 1
bij const

11.

3
z b0 x x
b1
1
b2
2
b1 , b2 const

12.

В дальнейшем мы будем рассматривать частный
случай функции нескольких переменных функцию
двух
переменных,
которая
обозначается как
z f ( x, y )
Ее
областью
определения
Х
является
подмножество координатной плоскости ХОУ.

13.

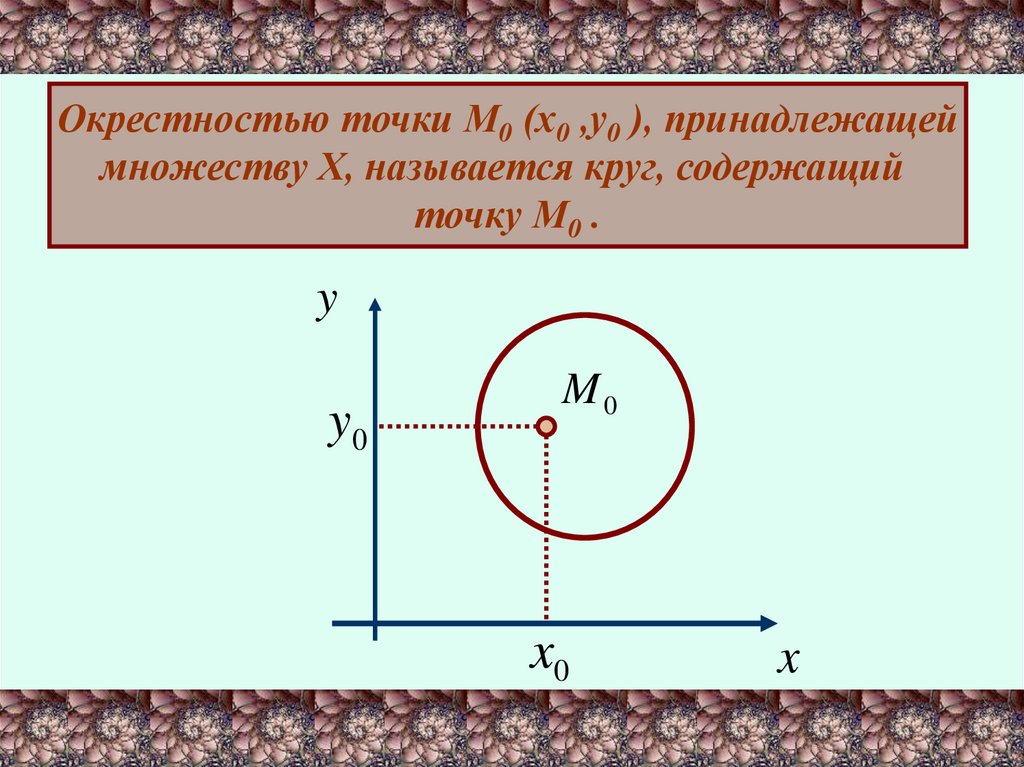
Окрестностью точки М0 (х0 ,у0 ), принадлежащей
множеству Х, называется круг, содержащий
точку М0 .
y
y0
M0
x0
x

14.

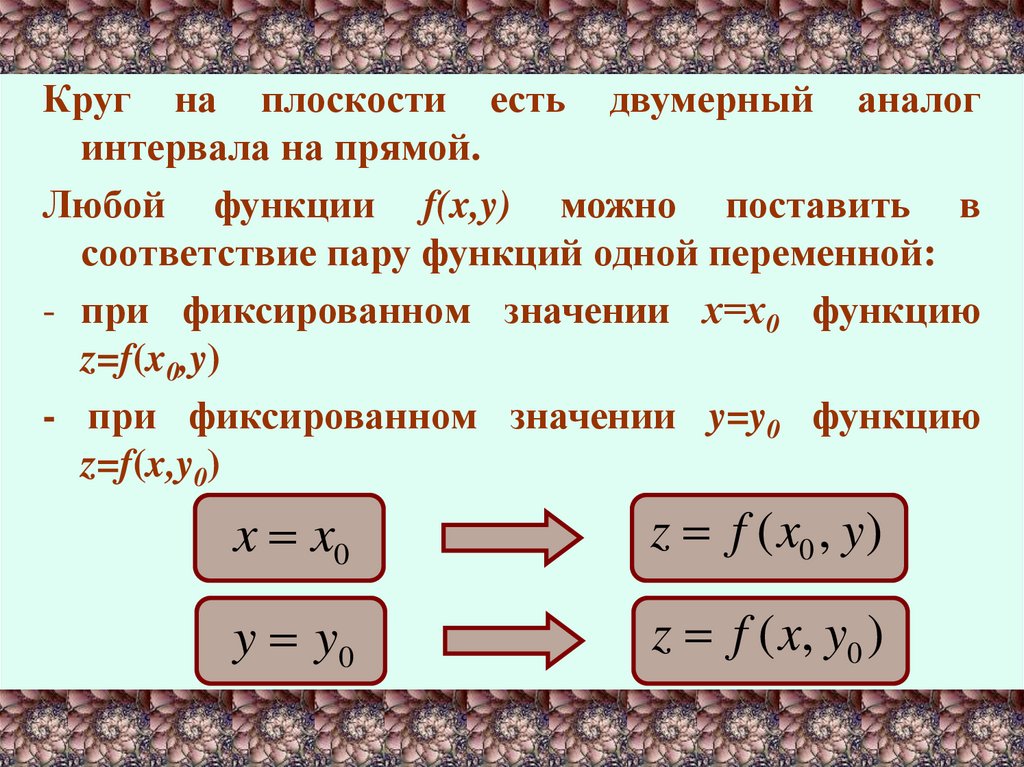
Круг на плоскости есть двумерный аналог
интервала на прямой.
Любой функции f(x,y) можно поставить в
соответствие пару функций одной переменной:
- при фиксированном значении х=х0 функцию
z=f(x0,y)
- при фиксированном значении y=y0 функцию
z=f(x,y0)
x x0
z f ( x0 , y)
y y0
z f ( x, y0 )

15.

Хотя функции
z f ( x0 , y)
z f ( x, y0 )
имеют одинаковое происхождение, их вид может
существенно отличаться.
Например, функция
z (1 x)
y
является степенной по переменной
показательной по переменной у.
х,
и

16.

Графиком функции двух переменных z=f(x,y)
называется множество точек трехмерного
пространства (x,y,z), аппликата которых
связана с абсциссой и ординатой
соотношением z=f(x,y).

17.

Для построение графика функции f(x,y) полезно
рассмотреть функции одной переменной:
z=f(x0,y) и z=f(x,y0)
которые
есть
сечения
графика
z=f(x,y)
плоскостями, параллельными координатным
плоскостям XOZ и YOZ, т.е. плоскостями
y=y0 и x=x0

18.

Построить график функции:
z x y 2y
2
2

19.

Найдем
сечения
поверхности
плоскостями,
параллельными координатным плоскостям.
Для этого преобразуем функцию к виду:
z x y 2 y x ( y 1) 1
2
2
2
При у=0 (сечение плоскостью XOZ):
z x
2
- парабола
2

20.

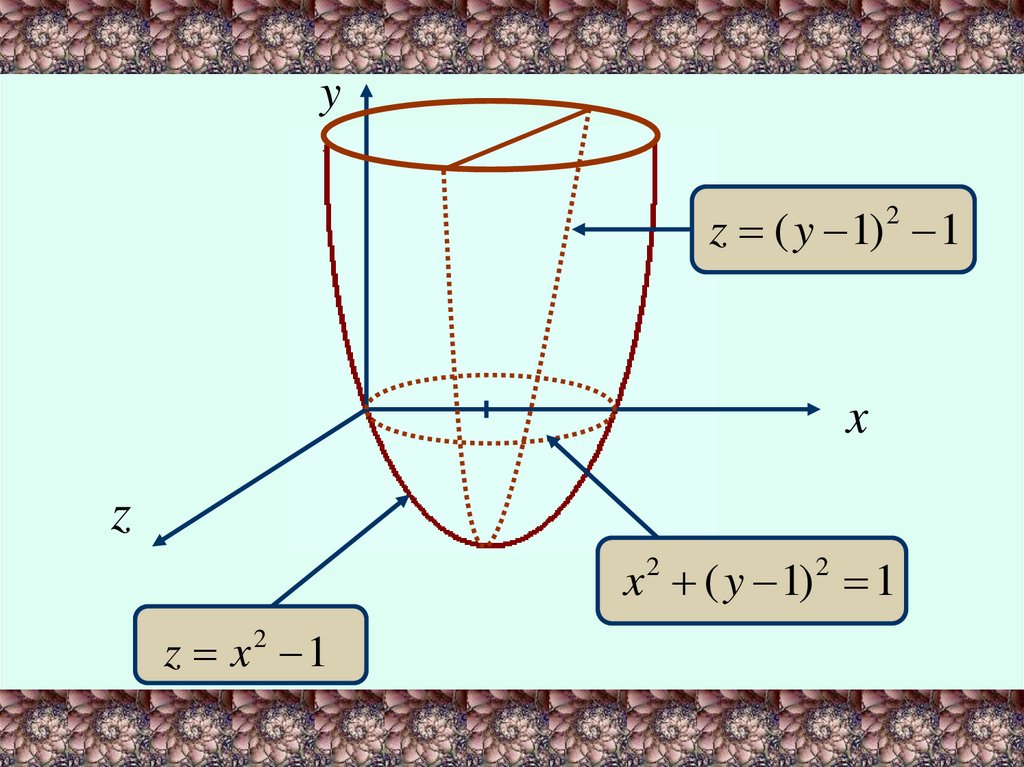
При х=0 (сечение плоскостью YOZ):
z ( y 1) 1
2
- парабола
При z=0 (сечение плоскостью XOY):
x ( y 1) 1
2
2
- окружность с центром в точке (0, 1)
Эта поверхность называется параболоидом.

21.

y
z ( y 1) 1
2
x
z
x 2 ( y 1) 2 1
z x 1
2

22.

Линией уровня функции двух переменных
z=f(x,y) называется множество точек на
плоскости, таких что во всех этих точках
значение функции одно и то же и равно С.
Число С называется уровнем.

23.

y
x
z

24.

Построить линии уровня функции:
z x y 2y
2
2

25.

Линия уровня z=C – это кривая на плоскости XOY,
которая задается уравнением
C x y 2y
2
2
или
C x ( y 1) 1
2
2
x ( y 1) C 1
2
2

26.

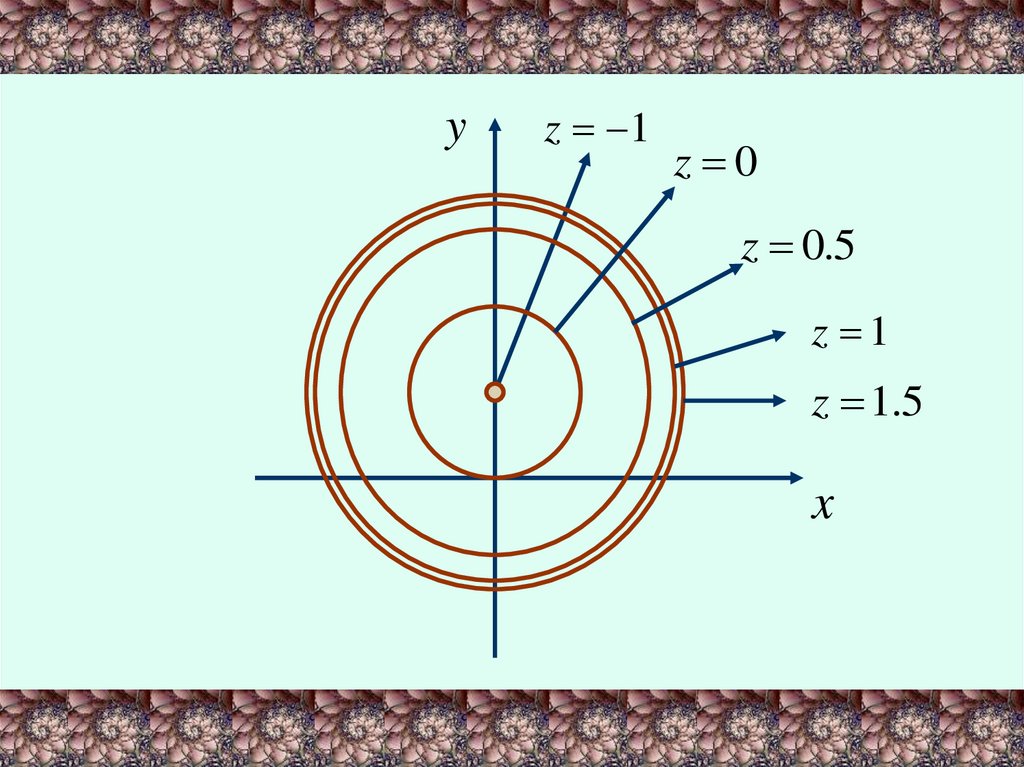
Это будет окружность с центром в точке (0,1) и
радиусом R C 1
При С=-1 имеем точку (0,1).
При С=0 имеем окружность с
При С=0.5 имеем окружность с
R 1.5
При С=1 имеем окружность с
R 2
И так далее.
R 1

27.

y
z 1
z 0
z 0.5
z 1
z 1.5
x

28.

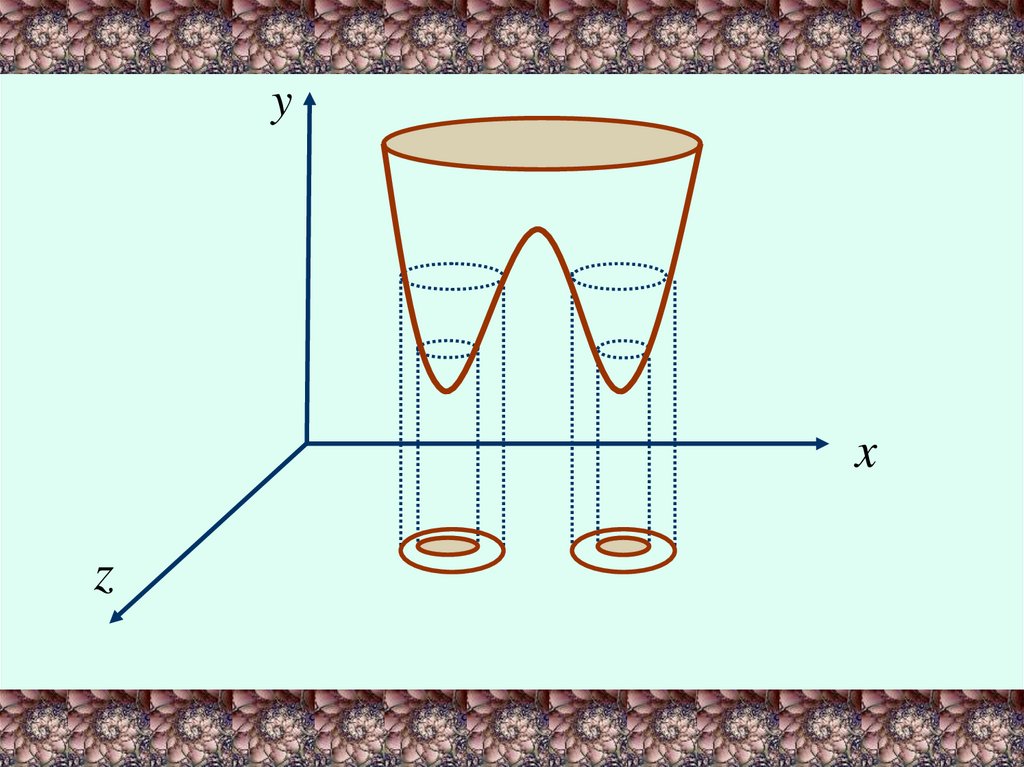
Линия уровня позволяют представить график
данной функции.
Расстояния между линиями с одинаковым шагом
уровня уменьшаются при удалении от центра.

29.

Число А называется пределом функции
z=f(x,y) при x x0 и y y0
если для любого,даже сколь угодно
малого числа ε>0, найдется такое
положительное число δ, что для всех
точек (х,у), отстоящих от точки
(х0,у0) на расстояние ρ>δ, выполняется
неравенство:

30.

f ( x, y) A
lim f ( x, y) A
x x0
y y0

31.

Вычислить предел функции,
когда оба аргумента
стремятся к нулю.
f ( x, y )
ln( 1 x 2 y 2 )
x2 y2

32.

x y
2
ln( 1 x y )
2
lim
x 0
y 0
lim
0
x y
2
2
2
ln( 1 2 )
при
2
x 0 y 0
0
1
0
lim
2 0
2
0 0 1

33.

Вычисление пределов функции одной
переменной является менее сложной
задачей, чем вычисление пределов
функции двух переменных.
Это происходит потому, что на
прямой всего два направления, по
которым
аргумент
может
стремиться к предельной точке
(справа и слева), а на плоскости
таких
направлений
бесконечно
много и пределы функций по
разным направлениям могут не
совпадать.

34.

Функция z=f(x,y) называется непрерывной
в точке (х0,у0), если она
1
Определена в точке (х0,у0)
2
Имеет конечный предел при
3
Этот предел равен значению
функции в точке (х0,у0)
x x0
и
y y0

35.

lim f ( x, y ) f ( x0 , y0 )
x x0
y y0