Похожие презентации:
Функция нескольких переменных
1. Лекция № 1
Функция несколькихпеременных
2. Вопросы
1. Понятие функции двух и болеепеременных.
2. Дифференцирование функции
нескольких переменных.
3. Частные производные. Полный
дифференциал.
4. Экстремум функции двух переменных.
3.
1. Рассмотрим функцию двухпеременных.
Опр. Если каждой паре независимых друг
от друга чисел (х, у) из некоторого
множества по какому - либо правилу
ставится в соответствие одно значение
переменной z, то она называется
функцией двух переменных.
z = f(x, y)
4.
Опр. Областью определения функцииz называется совокупность пар (х, у),
при которых функция z существует.
Опр. Окрестностью точки М0(х0, у0)
радиуса r называется совокупность всех
точек (х, у), которые удовлетворяют
условию
x x0 y y 0
2
2
r
.
5.
Опр. Число А называется пределомфункции f(x, y) при стремлении точки
М(х, у) к точке М0(х0, у0), если для
любого числа > 0 найдется такое
число r > 0, что для любой точки М(х, у),
для которых верно условие MM r
0
также верно и условие
f ( x, y) A
Записывают:
lim f ( x, y) A
x x0
y y0
6.
Опр. Пусть точка М0(х0, у0) принадлежитобласти определения функции f(x, y).
Тогда функция z = f(x, y) называется
непрерывной в точке М0(х0, у0), если
lim f ( x, y ) f ( x0 , y 0 )
x x0
y y0
причем точка М(х, у) стремится к точке
М0(х0, у0) произвольным образом.
(1)
7.
Если в какой – либо точке условие (1) невыполняется, то эта точка называется
точкой разрыва функции f(x, y). Это
может быть в следующих случаях:
1. Функция z = f(x, y) не определена в
точке М0(х0, у0).
2. Не существует предел в точке
М0(х0, у0).
3. Этот предел существует, но он не равен
f( x0, y0).
8.
2. Дифференцирование функциинескольких переменных
Опр. Пусть в некоторой области задана
функция z = f(x, y). Возьмем
произвольную точку М(х, у) и дадим
приращение х переменной х. Тогда
величина zx = f( x + x, y) – f(x, y)
называется частным приращением
функции по х.
9.
Можно записатьz х
f ( x x, y) f ( x, y)
x
x
z х
Тогда
lim
x 0 x
называется частной производной
функции z = f(x, y) по х.
10.
Обозначение:z
; z x ;
x
f ( x, y )
;
x
f x ( x, y ).
Аналогично определяется частная
производная функции по у:
z
f ( x, y y ) f ( x, y)
lim
y y 0
y
11.
Полное приращение и полныйдифференциал
Опр. Для функции f(x, y) выражение
z = f( x + x, y + y) – f(x, y)
называется полным приращением.
Полное приращение функции f(x, y) в
некоторой точке (х, у), можно
представить как
f ( x, y)
f ( x, y)
z
x
y 1 x 2 y
x
y
12.
где 1 и 2 – бесконечно малые функциипри х 0 и у 0 соответственно.
Опр. Полным дифференциалом
функции z = f(x, y) называется главная
линейная относительно х и у часть
приращения функции z в точке (х, у).
dz f x ( x, y )dx f y ( x, y )dy
13.
Для функции произвольного числапеременных:
f
f
f
df ( x, y, z,..., t ) dx dy ... dt
x
y
t
Пример 1. Найти полный дифференциал
функции
2
u x
y z
.
14.
*u
u
u
du
dx
dy
dz
x
y
z
u
u
u
2
y 2 z 1
y2z
y2z
2
y zx ;
x ln x 2 yz;
x ln x y ;
x
y
z
du y zx
2
y 2 z 1
y2 z
2 y2z
dx 2x yz ln xdy y x ln xdz
15.
Пример 2. Найти полный дифференциалy
функции
z
x y
2
.
2
Находим частные производные:
z
2 yx
2
2 2
x ( x y )
z ( x y ) y( 2 y) x y 2 y
x y
2 22 2 22
2
2 2
y
(x y )
(x y )
(x y )
2
2
2
2
2
2
2
16.
Получаем2 xy
x y
dz 2 2 2 dx 2 2 2 dy
(x y )
(x y )
2
2
Частные производные высших
порядков
Если функция f(x, y) определена в
некоторой области D, то ее частные
производные
f x ( x, y)
f y ( x, y )
тоже будут определены в той же области
или ее части.
17.
Будем называть эти производныечастными производными первого
порядка.
Производные этих функций будут
частными производными второго
порядка.
z
f
(
x
,
y
);
xx
2
x
2
z
f xy ( x, y);
x y
2
z
f
(
x
,
y
);
yy
2
y
2
z
f yx ( x, y);
y x
2
18.
Продолжая дифференцироватьполученные равенства, получим
частные производные более высоких
порядков.
Опр. Частные производные вида
z z
z
z
;
;
;
x y y x x y x x y y
2
2
3
и т.д. называются смешанными
производными.
3
19.
Теорема. Если функция f(x, y) и еечастные производные определены и
непрерывны в точке М(х, у) и ее
окрестности, то верно соотношение:
f
f
x y
y x
2
2
т.е. частные производные высших
порядков не зависят от порядка
дифференцирования.
20.
Пример 3. Найти частные производные 1го и 2-го порядков функций1)
2
2
u x 3xy 4 y x 2 y 1
Решение. Рассматривая у как постоянную
величину, получим
u
2x 3y 1
x
21.
Рассматривая х как постоянную величину,найдем
u
3x 8 y 2
у
2
u u
2
;
Далее,
2
x x
x
u u
8
;
2
y y
y
2
22.
*u
u
3;
x y y x
2
u
u
3.
y x x y
2
u
u
.
x y y x
2
Имеем,
2
23.
2)z e
x y
2
2
Решение. Рассматривая у как постоянную
величину, получим
z
x2 y 2
2
2 '
x2 y2
e
( x y ) x 2 xe
x
Рассматривая х как постоянную величину,
найдем
z
x2 y2
2
2 '
x2 y 2
e
( x y ) y 2 ye
y
24.
Далее,z
x2 y 2
x2 y2
x2 y2
2 xe
xe
2x
x 2e
2
x
2
2e
x2 y 2
1 2 x ;
2
z
x2 y2
x2 y2
x2 y2
2 ye
ye
2y
y 2e
2
y
2
2e
x2 y2
1 2 y ;
2
25.
*2z
x2 y 2
x2 y 2
x2 y 2
2 xe
2 y 4 xye
;
y 2 xe
x y
2z
x2 y2
x2 y2
x2 y 2
2 ye
2 x 4 xye
.
x 2 ye
y x
Имеем,
u
u
.
x y y x
2
2
26.
3. Экстремум функции несколькихпеременных
Опр. Если для функции z = f(x, y),
определенной в некоторой области, в
некоторой окрестности точки М0(х0, у0)
верно неравенство
f ( x0 , y0 ) f ( x, y)
то точка М0 называется точкой
максимума.
27.
Опр. Если для функции z = f(x, y),определенной в некоторой области, в
некоторой окрестности точки М0(х0, у0)
верно неравенство
f ( x0 , y0 ) f ( x, y)
то точка М0 называется точкой
минимума.
28.
Теорема. (Необходимые условияэкстремума).
Если функция f(x,y) в точке (х0, у0) имеет
экстремум, то в этой точке либо обе ее
частные производные первого порядка
равны нулю
f x ( x0 , y 0 ) 0,
f y ( x0 , y 0 ) 0
либо хотя бы одна из них не существует.
Эту точку (х0, у0) будем называть
критической точкой.
29.
Теорема. (Достаточные условияэкстремума).
Пусть в окрестности критической точки
(х0, у0) функция f(x, y) имеет
непрерывные частные производные до
второго порядка включительно.
Рассмотрим выражение:
( x, y ) f ( x, y ) f ( x, y ) f ( x, y )
''
x2
''
y2
''
xy
2
30.
1. Если Δ(x0, y0) > 0, то в точке (х0, у0)функция f(x, y) имеет экстремум,
если f 2 ( x , y ) 0 - максимум,
x
если
0
0
f x 2 ( x0 , y 0 ) 0 - минимум.
2. Если Δ(x0, y0) < 0, то в точке (х0, у0)
функция f(x, y) не имеет экстремума.
3. В случае, если Δ = 0, вывод о наличии
экстремума сделать нельзя.
31.
*Пример 4. Найти экстремум функцииz x xy y 3x 6 y
2
2
Решение. Найдем частные производные
первого порядка:
z
z
2 x y 3,
x 2y 6
x
y
Используя необходимые условия
экстремума, находим стационарные
точки:
32.
*2 x y 3 0,
x 2 y 6 0,
Откуда х = 0, у = 3; М(0;3).
Находим значения частных производных
второго порядка в точке М:
z
z
z
2
,
2
,
1
2
2
x y
x
y
2
2
2
33.
*и составляем выражение2
( x, y ) f ( x, y ) f ( x, y ) f ( x, y )
''
x2
''
y2
''
xy
2 2 1 3 0
z
,
2
0
2
x
то функция в точке М(0;3) имеет
минимум. Значение функции в этой
точке
Так как
2
z min 9
34.
Пример 5.Найти область определенияфункции
z 25 x y
2
2
Решение. Функция принимает
действительное значение при условии
25 x y 0
2
2
x
y
25
т.е.
2
2
Областью определения данной функции
является круг радиуса 5 с центром в
начале координат, включая граничную
окружность.
35.
Метод множителей ЛагранжаУсловный экстремум
Условный экстремум находится, когда
переменные х и у, входящие в функцию
u = f( x, y), не являются независимыми, т.е.
существует некоторое соотношение
(х, у) = 0, которое называется уравнением
связи.
Тогда из переменных х и у только одна будет
независимой, так как другая может быть
выражена через нее из уравнения связи.
36.
Тогда u = f(x, y(x)).du f f dy
dx x y dx
В точках экстремума:
du f f dy =0 (1)
dx x y dx
Кроме того:
dy
0 (2)
x y dx
37.
Умножим равенство (2) на число исложим с равенством (1).
f f dy
dy
0
x y dx
x y dx
f
dy
f
0
x y
y dx
x
38.
Для выполнения этого условия во всехточках найдем неопределенный
коэффициент так, чтобы выполнялась
система трех уравнений:
f
x x 0
f
0
y
y
( x, y ) 0
39.
Полученная система уравнений являетсянеобходимыми условиями условного
экстремума. Однако это условие не
является достаточным. Поэтому при
нахождении критических точек
требуется их дополнительное
исследование на экстремум.
Выражение u = f(x, y) + (x, y)
называется функцией Лагранжа.
40.
Пример. Найти экстремум функцииf(x, y) = xy, если уравнение связи:
2x + 3y – 5 = 0.
Решение. Составим функцию Лагранжа
u xy (2 x 3 y 5)
u
y 2 ;
x
u
x 3 ;
y
41. Имеем
*y 2 0
x 3 0
2 x 3 y 5 0
5
;
12
.
5
x ;
4
5
y ;
6
Таким образом, функция имеет экстремум
в точке
5 5
;
4 6
42.
Использование функции Лагранжа длянахождения точек экстремума функции
называется также методом
множителей Лагранжа.
Выше мы рассмотрели функцию двух
переменных, однако, все рассуждения
относительно условного экстремума
могут быть распространены на функции
большего числа переменных.













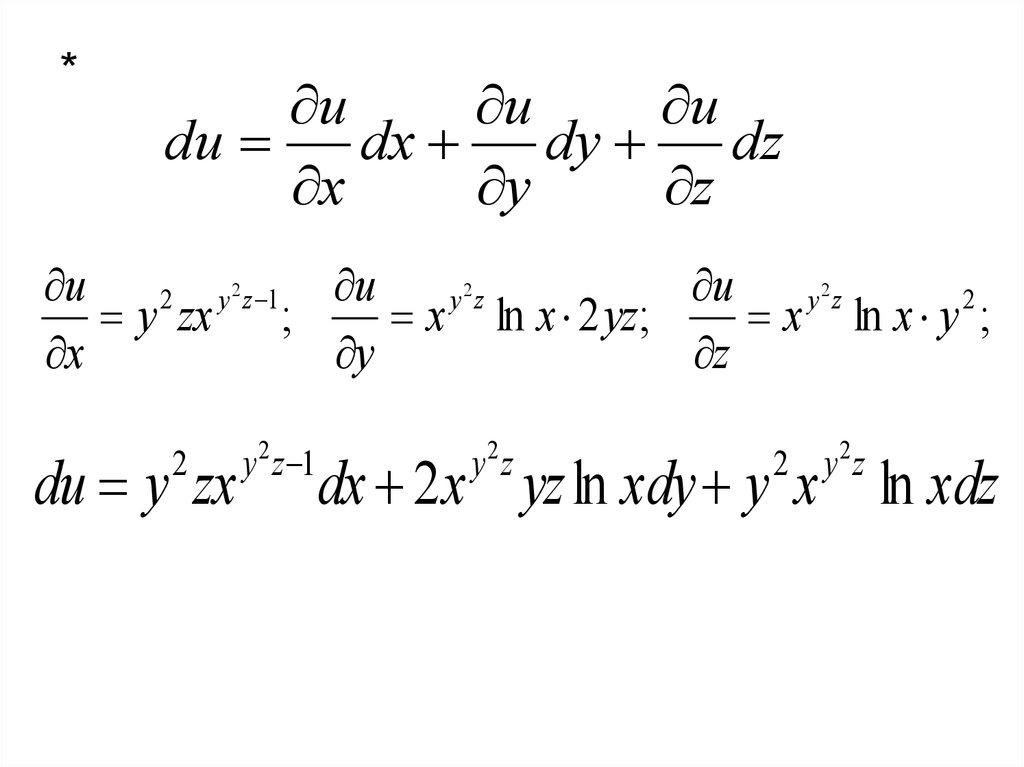









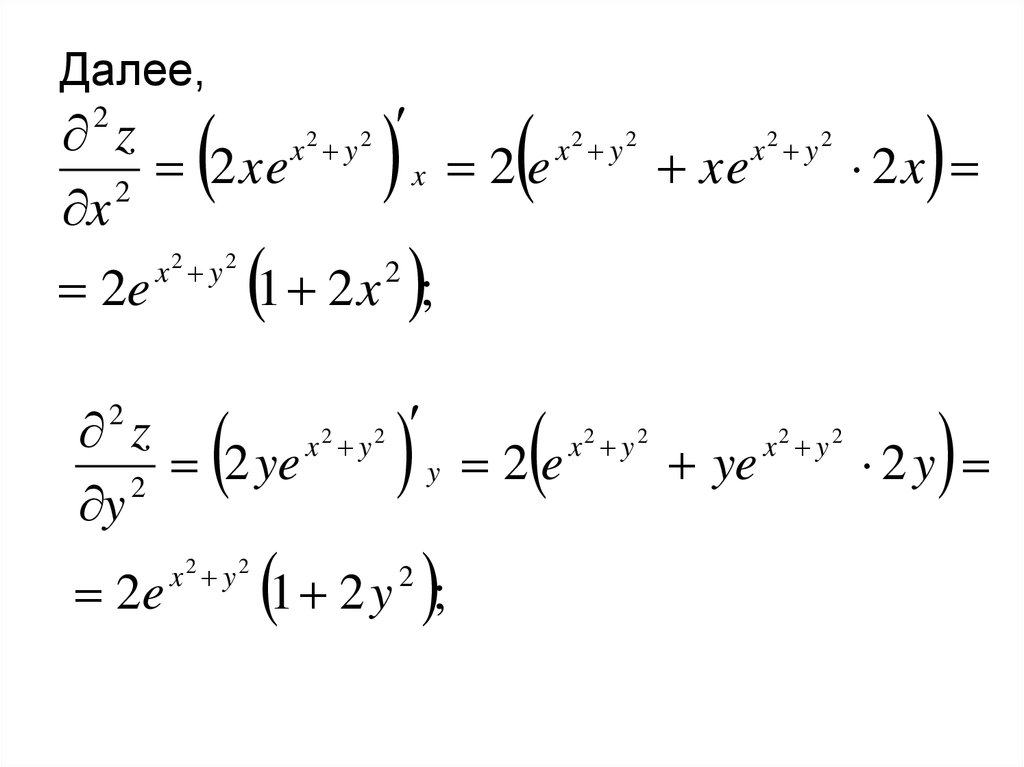


















 Математика
Математика








