Похожие презентации:
Пересечение поверхности вращения плоскостью. Развертка нижней отсеченной части конуса. Лекция 11
1. Лекция 11
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
"САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА»
(САМАРСКИЙ УНИВЕРСИТЕТ)
Лекция 11
Пересечение поверхности
вращения плоскостью.
Развертка нижней
отсеченной части конуса.
2.
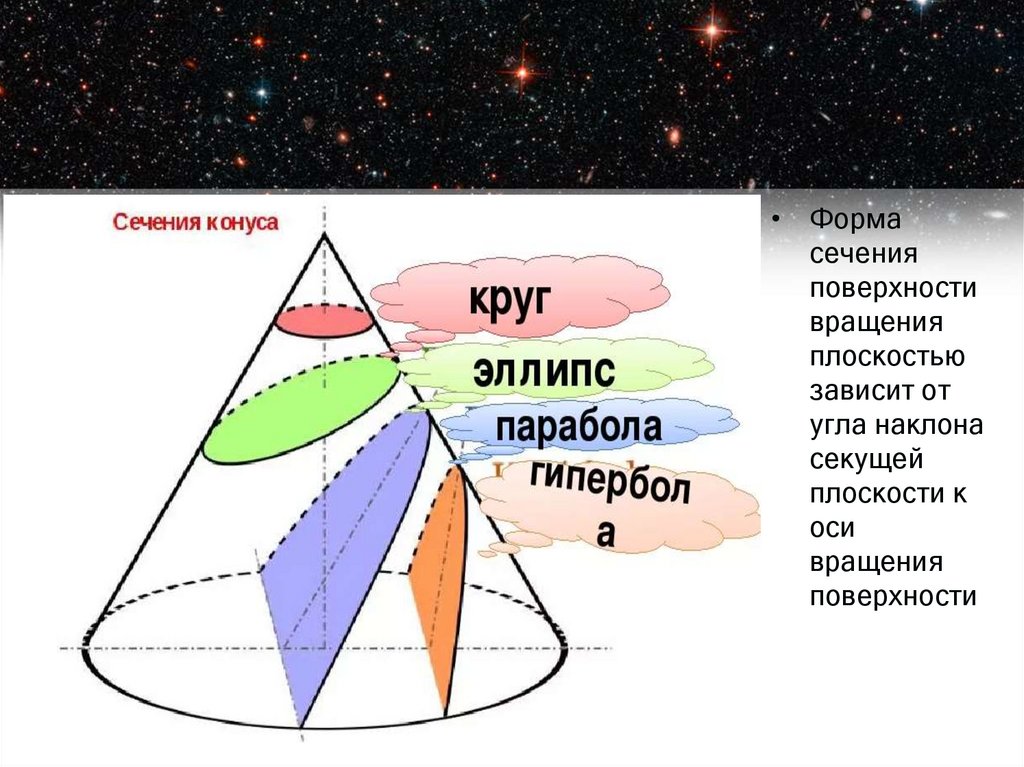
• Формасечения
поверхности
вращения
плоскостью
зависит от
угла наклона
секущей
плоскости к
оси
вращения
поверхности
3.
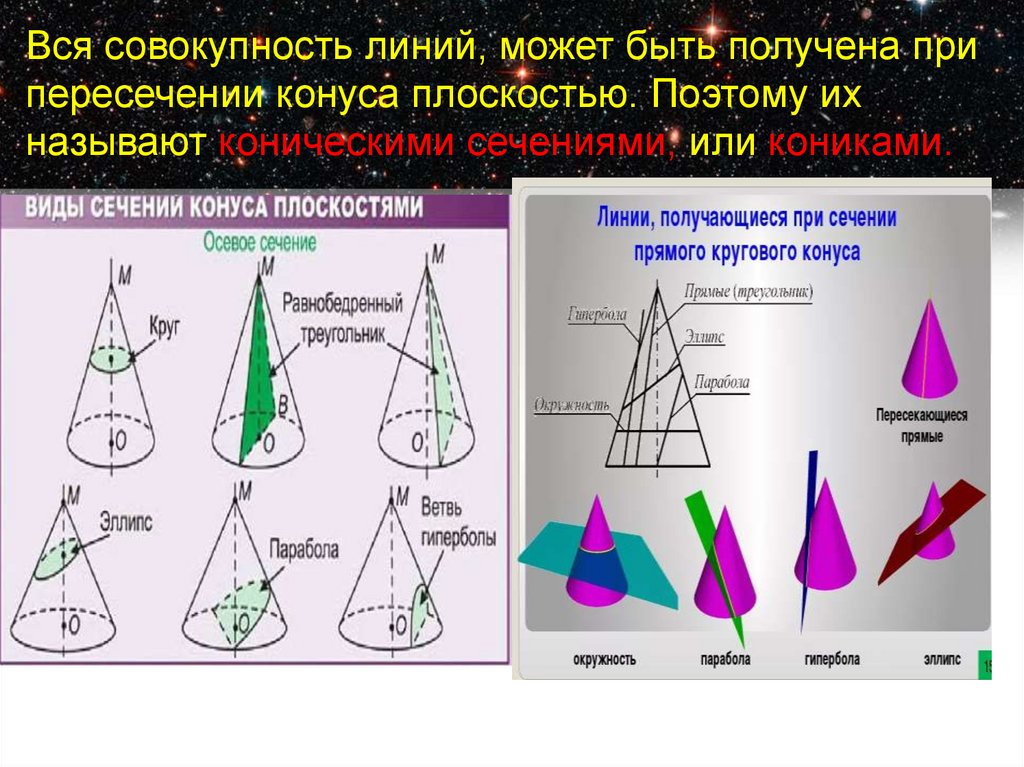
Вся совокупность линий, может быть получена припересечении конуса плоскостью. Поэтому их
называют коническими сечениями, или кониками.
4.
Сечения прямого кругового конуса1
3
5
3
4
1
2
2
4
При пересечении прямого кругового конуса с
плоскостью в зависимости от ее расположения
получаются:
1 – окружность; 2 – эллипс; 3 – парабола; 4 – гипербола;
5 – прямые линии
5
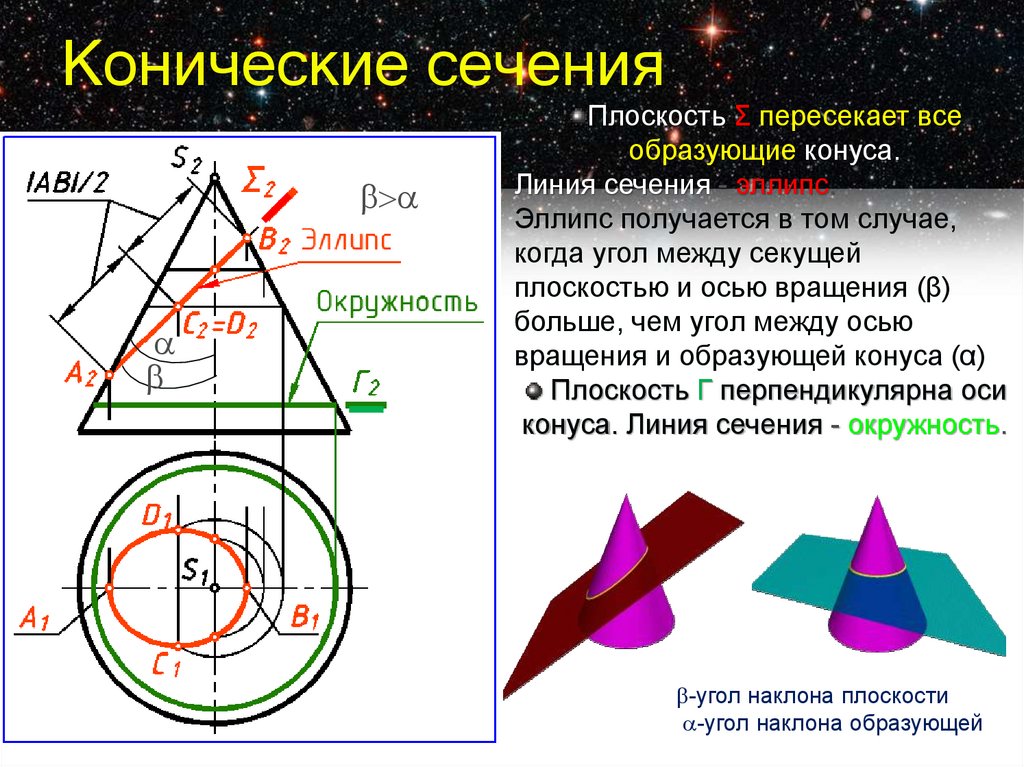
5. Конические сечения
Плоскость Σ пересекает всеобразующие конуса.
Линия сечения - эллипс.
Эллипс получается в том случае,
когда угол между секущей
плоскостью и осью вращения (β)
больше, чем угол между осью
вращения и образующей конуса (α)
Плоскость Г перпендикулярна оси
конуса. Линия сечения - окружность.
-угол наклона плоскости
-угол наклона образующей
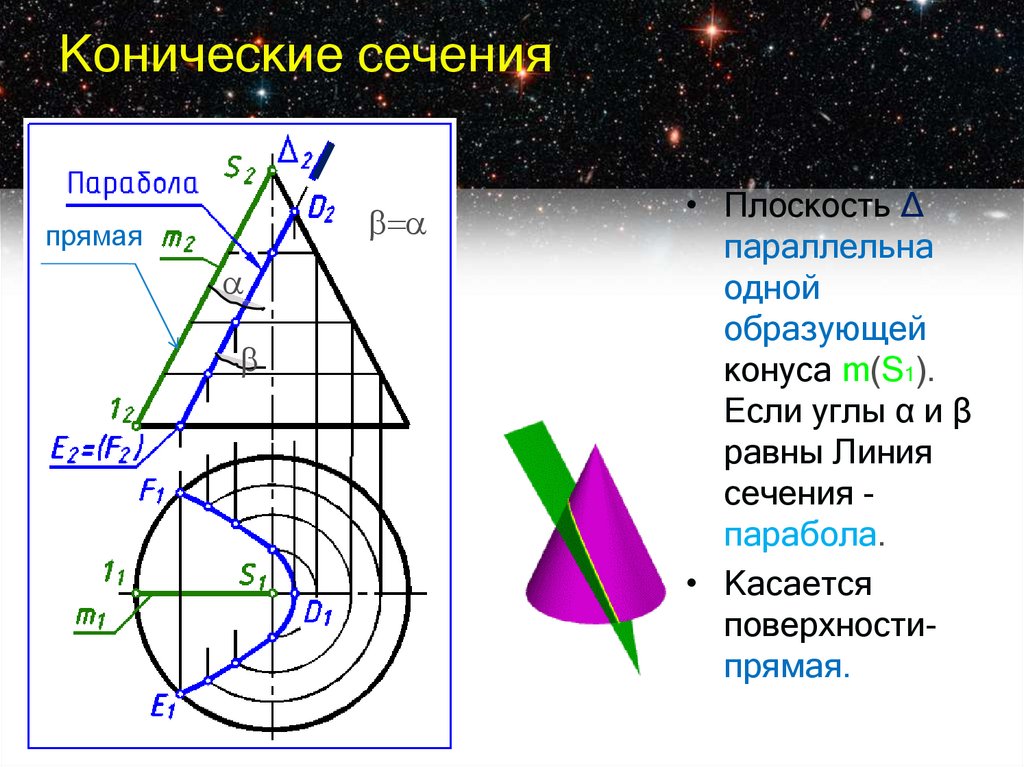
6. Конические сечения
прямая• Плоскость Δ
параллельна
одной
образующей
конуса m(S1).
Если углы α и β
равны Линия
сечения парабола.
• Касается
поверхностипрямая.
7. Конические сечения
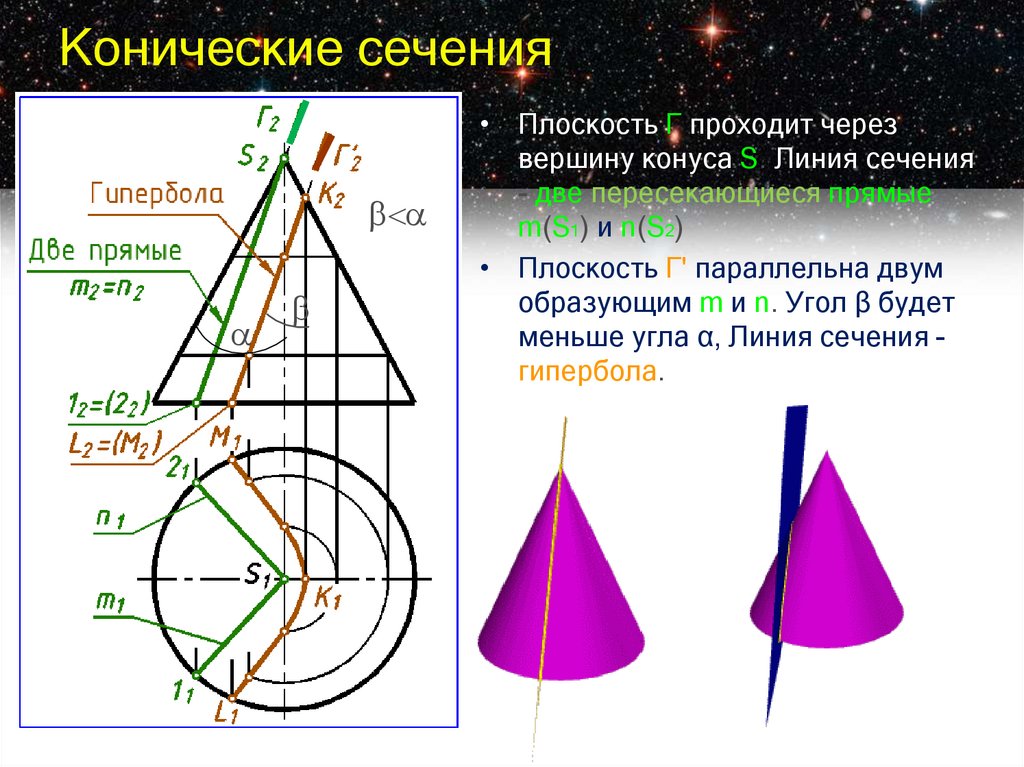
• Плоскость Г проходит черезвершину конуса S. Линия сечения
- две пересекающиеся прямые
m(S1) и n(S2)
• Плоскость Г' параллельна двум
образующим m и n. Угол β будет
меньше угла α, Линия сечения гипербола.
8.
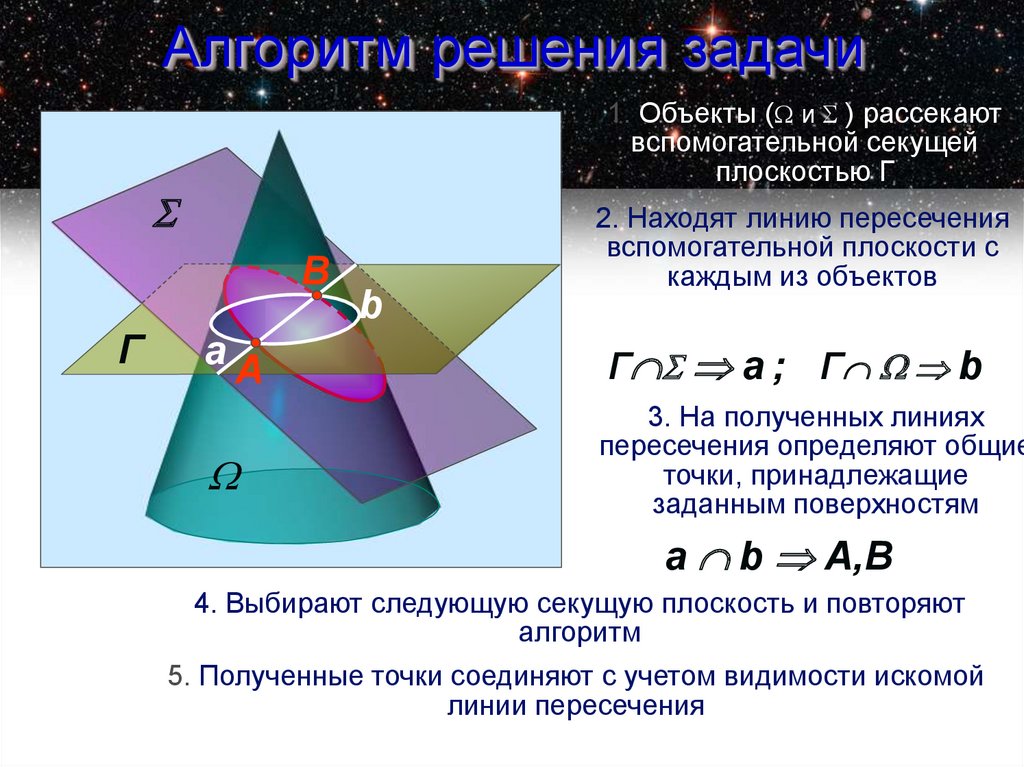
Алгоритм решения задачи1. Объекты ( и ) рассекают
вспомогательной секущей
плоскостью Г
B
Г
аА
b
2. Находят линию пересечения
вспомогательной плоскости с
каждым из объектов
Г а ; Г b
3. На полученных линиях
пересечения определяют общие
точки, принадлежащие
заданным поверхностям
a b A,B
4. Выбирают следующую секущую плоскость и повторяют
алгоритм
5. Полученные точки соединяют с учетом видимости искомой
линии пересечения
9.
Для построения линии пересечения необходимо найти общие точки поверхности и
заданной плоскости. Для определения этих точек необходимо ввести
дополнительные секущие плоскости, которые дают наиболее простые линии сечения –
окружности или ломаные прямые.
Построение линии сечения начинают с нахождения характерных точек сечения, к
которым относятся:
1) высшая и низшая точки;
2) крайняя левая и крайняя правая точки, в которых проекции линии сечения касаются
очерковых образующих ( точки, лежащие на границе видимости);
3) ближайшая и наиболее удаленная точки сечения.
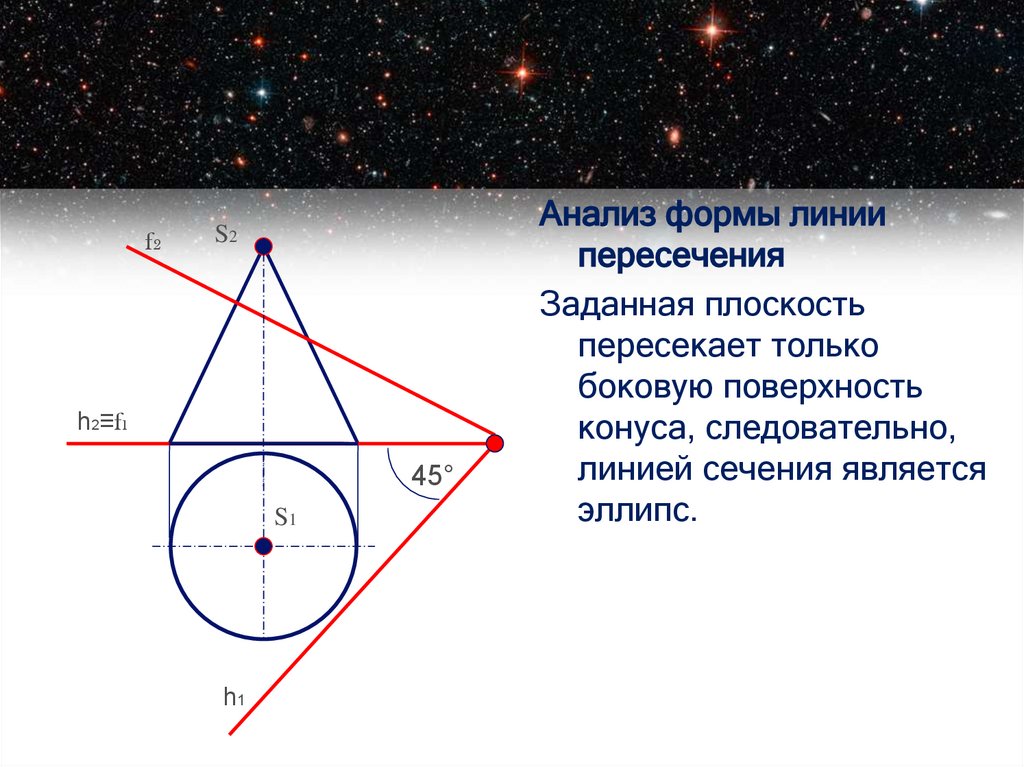
ПРИМЕР: Определить линию пересечения конуса плоскостью общего положения (h f).
Построить развертку нижней отсеченной поверхности конуса.
10.
f2S2
h2≡f1
45°
S1
h1
Анализ формы линии
пересечения
Заданная плоскость
пересекает только
боковую поверхность
конуса, следовательно,
линией сечения является
эллипс.
11.
f2S2
i2
Высшая и низшая точки сечения (А,В) определяют
большую ось эллипса и лежат на линии
наибольшего наклона плоскости
(h∩f) к плоскости основания конуса. Эти точки
определяются с помощью дополнительной
плоскости Σ, которая одновременно пересекает
поверхность и заданную плоскость. Эту плоскость
необходимо выбирать таким образом, чтобы она
пересекала поверхность вращения по параллелям
( окружностям) или образующим.
22
А2
В2
h2≡f1
42
32
12
21
41
А1
i1
S1
В1
31
11
h1
iϵΣ(Σ1) h (Σ1 h1)
∩ =(1-2) ] AB] ((1-2)∩Фк=АВ)
Σ∩ Фк=Δ 3-S-4 – сечение треугольник
АВ – большая ось эллипса
12.
f2S2
i2
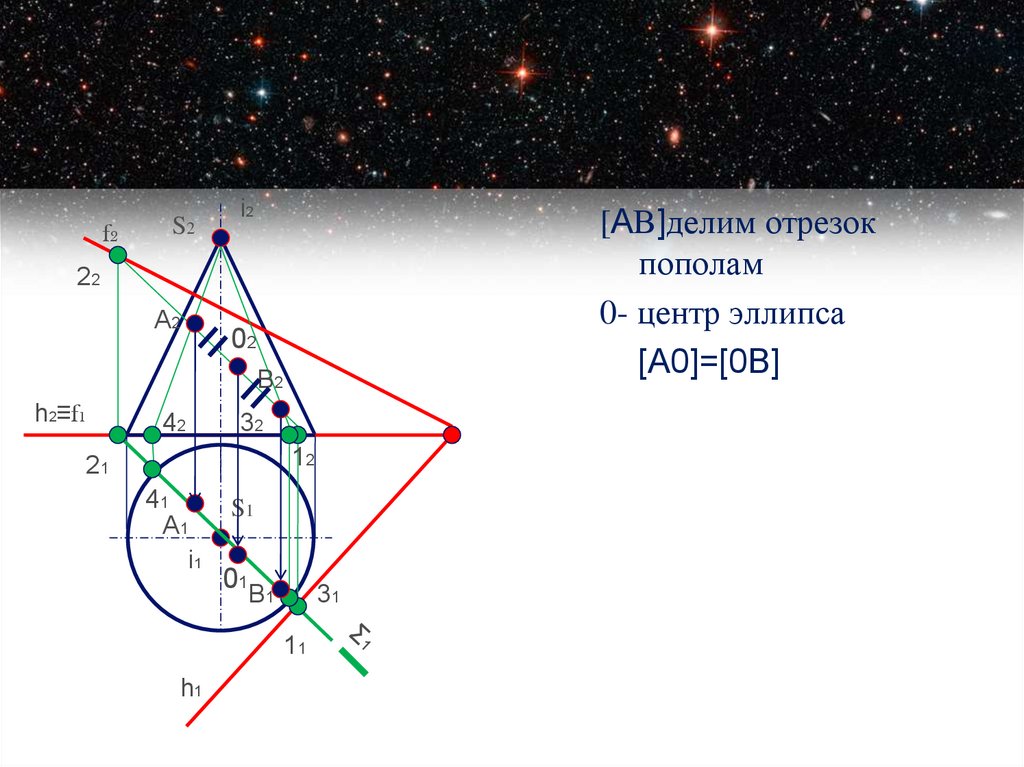
[AВ]делим отрезок
пополам
0- центр эллипса
[A0]=[0B]
22
А2
02
В2
h2≡f1
42
32
12
21
41
А1
i1
S1
01
В1
31
11
h1
13.
S2f2
i2
22
А2
Г2 hʹ2
С2
42
h2≡f1
02 D2
В2
32
12
21
41
S1 D1
А1
i1
01
С1
В1
31
hʹ1
11
h1
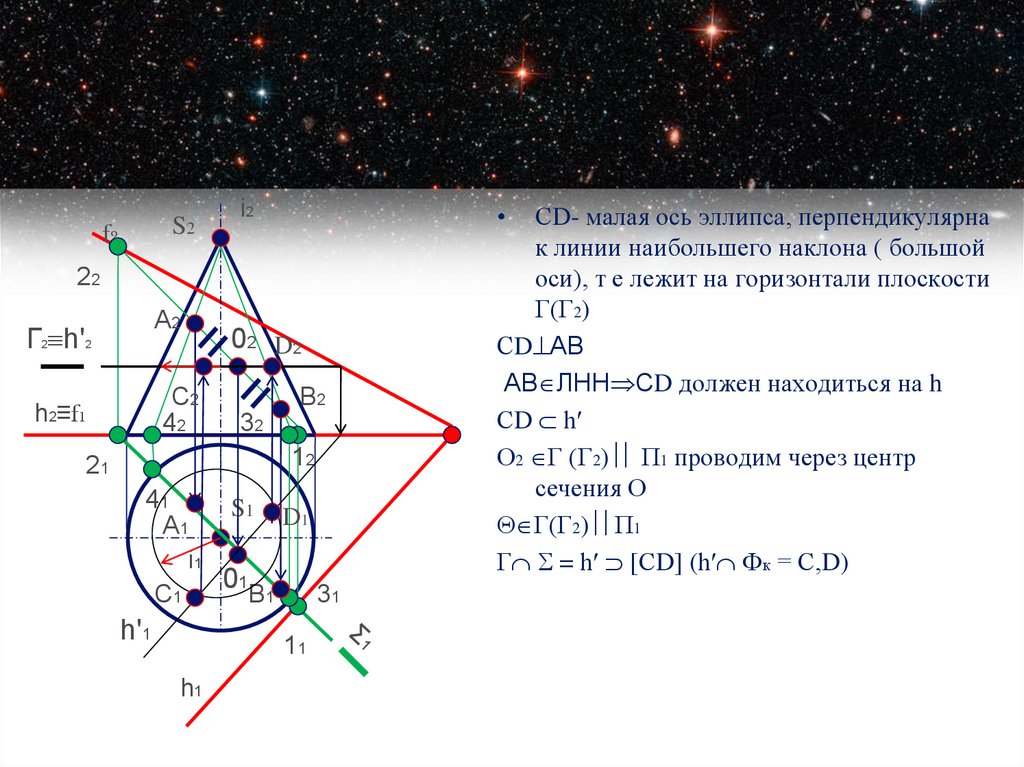
СD- малая ось эллипса, перпендикулярна
к линии наибольшего наклона ( большой
оси), т е лежит на горизонтали плоскости
Г(Г2)
СD AB
AB ЛНН СD должен находиться на h
СD hʹ
О2 Г (Г2) П1 проводим через центр
сечения О
Г(Г2) П1
Г = hʹ СD (hʹ Фк = С,D)
14.
f2f ʹ2
S2
22
i2
А2
Г2 hʹ2
02 D2
Е2
С2
42
h2≡f1
21
Ф1≡f ʹ1
12
А1
41
F2
В2
32
S1
D1 F1
Е1 i1
01
С1
В1
hʹ1
31
11
h1
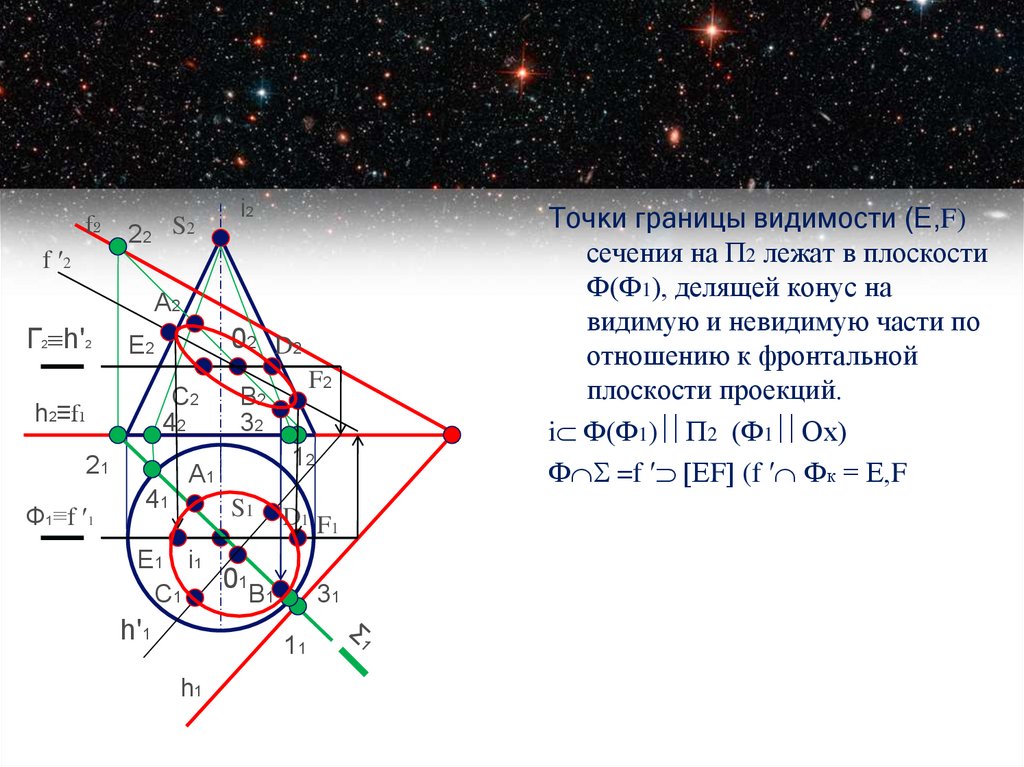
Точки границы видимости (Е,F)
сечения на П2 лежат в плоскости
Ф(Ф1), делящей конус на
видимую и невидимую части по
отношению к фронтальной
плоскости проекций.
i Ф(Ф1) П2 (Ф1 Ох)
Ф =f ʹ ЕF (f ʹ Фк = Е,F
15. Видимость
f2f ʹ2
S2
22
i2
А2
Г2 hʹ2
02 D2
Е2
С2
42
h2≡f1
21
Ф1≡f ʹ1
12
А1
41
F2
В2
32
S1
D1 F1
Е1 i1
01
С1
В1
hʹ1
31
11
h1
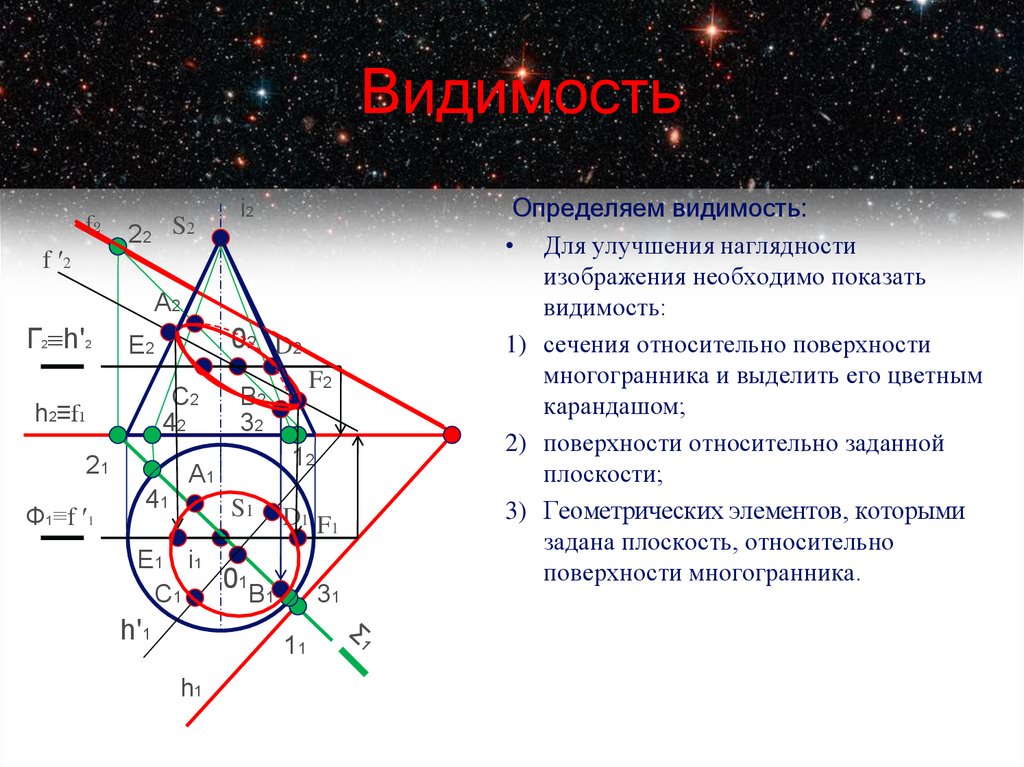
Определяем видимость:
• Для улучшения наглядности
изображения необходимо показать
видимость:
1) сечения относительно поверхности
многогранника и выделить его цветным
карандашом;
2) поверхности относительно заданной
плоскости;
3) Геометрических элементов, которыми
задана плоскость, относительно
поверхности многогранника.
16.
f2S2
f ʹ2
i2
А2
Г2 hʹ2
02 D2
Е2
С2
h2≡f1
А1
Ф1≡f ʹ1
D1
S1
Е1
i1
С1
hʹ1
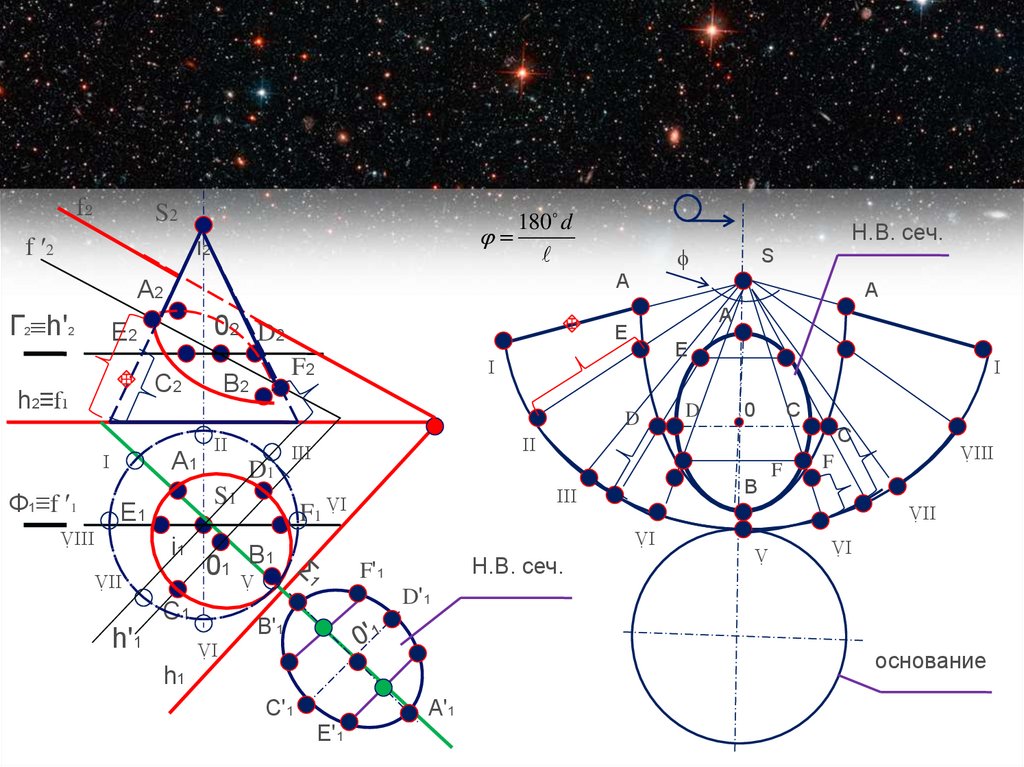
Натуральная величина
сечения определяется
вращением вокруг
линии уровня.
F2
В2
F1
01 В 1
Н.В. сеч.
Fʹ1
Dʹ1
Вʹ1
h1
Сʹ1
Аʹ1
Еʹ1
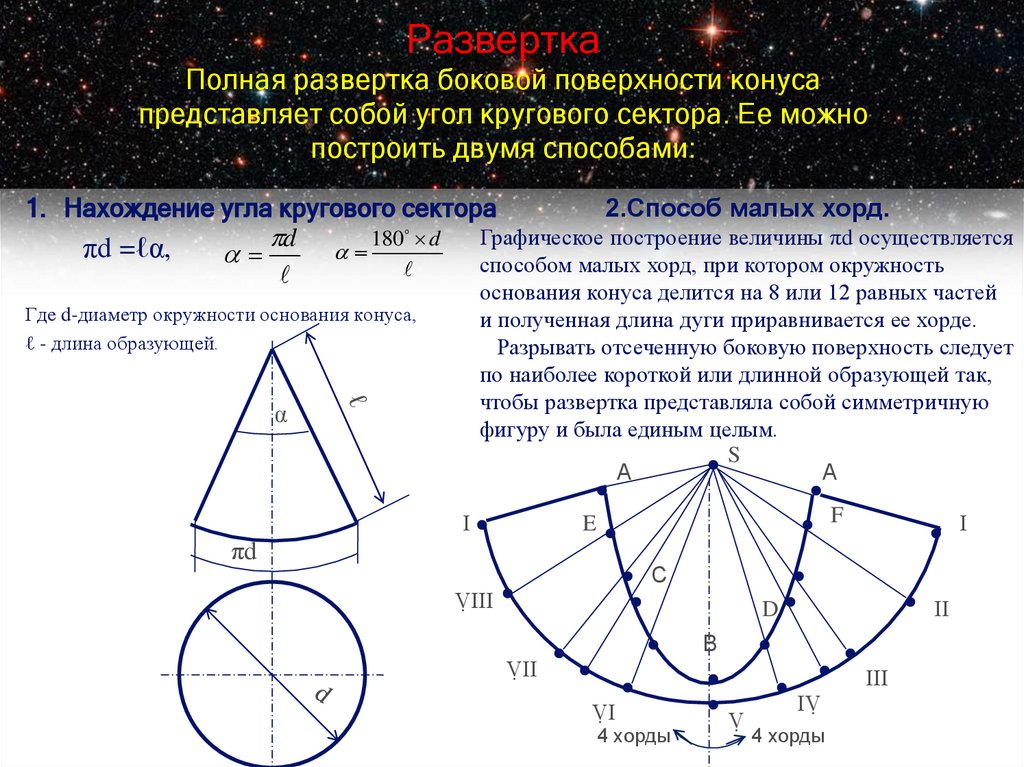
17. Развертка Полная развертка боковой поверхности конуса представляет собой угол кругового сектора. Ее можно построить двумя
способами:2.Способ малых хорд.
1. Нахождение угла кругового сектора
d 180 d Графическое построение величины πd осуществляется
πd =ℓα,
способом малых хорд, при котором окружность
основания конуса делится на 8 или 12 равных частей
и полученная длина дуги приравнивается ее хорде.
Разрывать отсеченную боковую поверхность следует
по наиболее короткой или длинной образующей так,
чтобы развертка представляла собой симметричную
фигуру и была единым целым.
S
А
А
Где d-диаметр окружности основания конуса,
ℓ - длина образующей.
α
Ι
F
E
πd
Ι
С
ṾΙΙΙ
ΙΙ
D
В
ṾΙΙ
ΙΙΙ
ṾΙ
4 хорды
Ṿ
ΙṾ
4 хорды
18.
f2S2
f ʹ2
180 d
i2
С2
В2
А
Е
Е
Ι
F2
А1
i1
ṾΙΙ
hʹ1
D1
01
С1
D
Ι
С
0
С
ΙΙ
ΙΙΙ
S1
Е1
ṾΙΙΙ
ΙΙ
S
А
D
Ι
Ф1≡f ʹ1
02 D2
Е2
h2≡f1
ϕ
А
А2
Г2 hʹ2
Н.В. сеч.
B
ΙΙΙ
F1 ṾΙ
Н.В. сеч.
Fʹ1
Ṿ
ṾΙΙΙ
F
ṾΙΙ
ṾΙ
В1
F
Ṿ
ṾΙ
Dʹ1
Вʹ1
ṾΙ
основание
h1
Сʹ1
Аʹ1
Еʹ1
19.
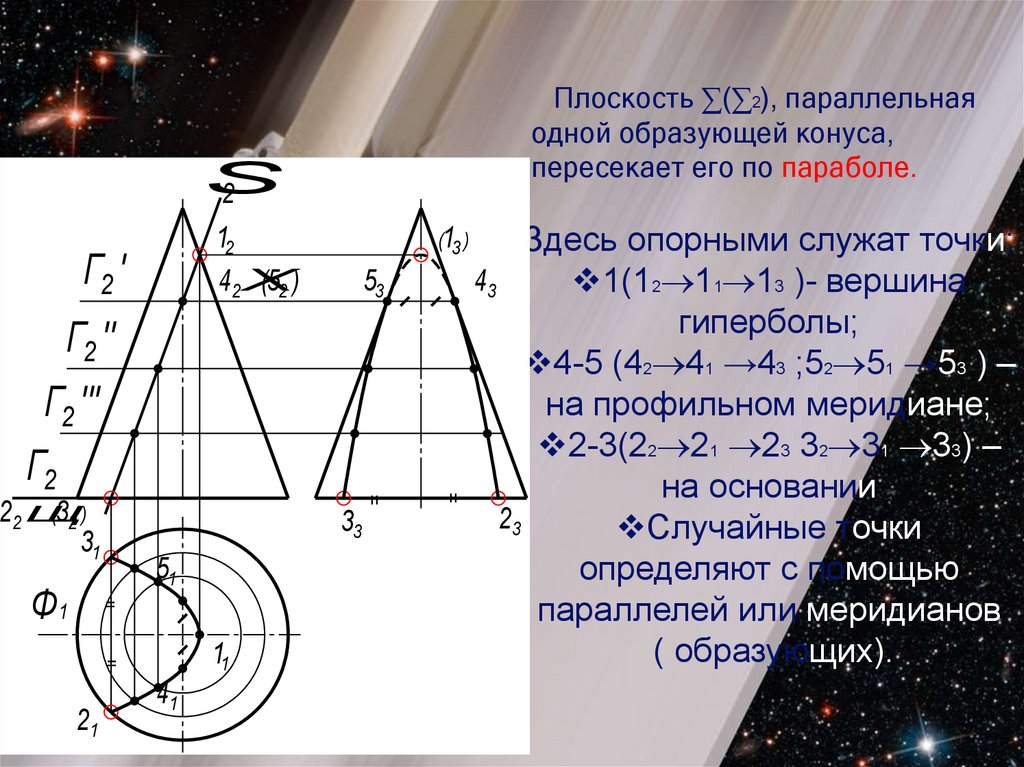
Плоскость ∑(∑2), параллельнаяодной образующей конуса,
пересекает его по параболе.
S
2
12
42 X
(52 )
Г2 '
(13 )
53
=
Г2 '''
Г2
22 Щ
(32 )
31
Ф1
33
51
=
11
=
21
41
=
Г2 ''
Здесь опорными служат точки:
43
1(12 11 13 )- вершина
гиперболы;
4-5 (42 41 →43 ;52 51 →53 ) –
на профильном меридиане;
2-3(22 21 23 32 31 33) –
на основании
23
Случайные точки
определяют с помощью
параллелей или меридианов
( образующих).
20.
Гʹ222
Гʹʹ2
Гʹʹʹ2
Г2
21
2ʹ1
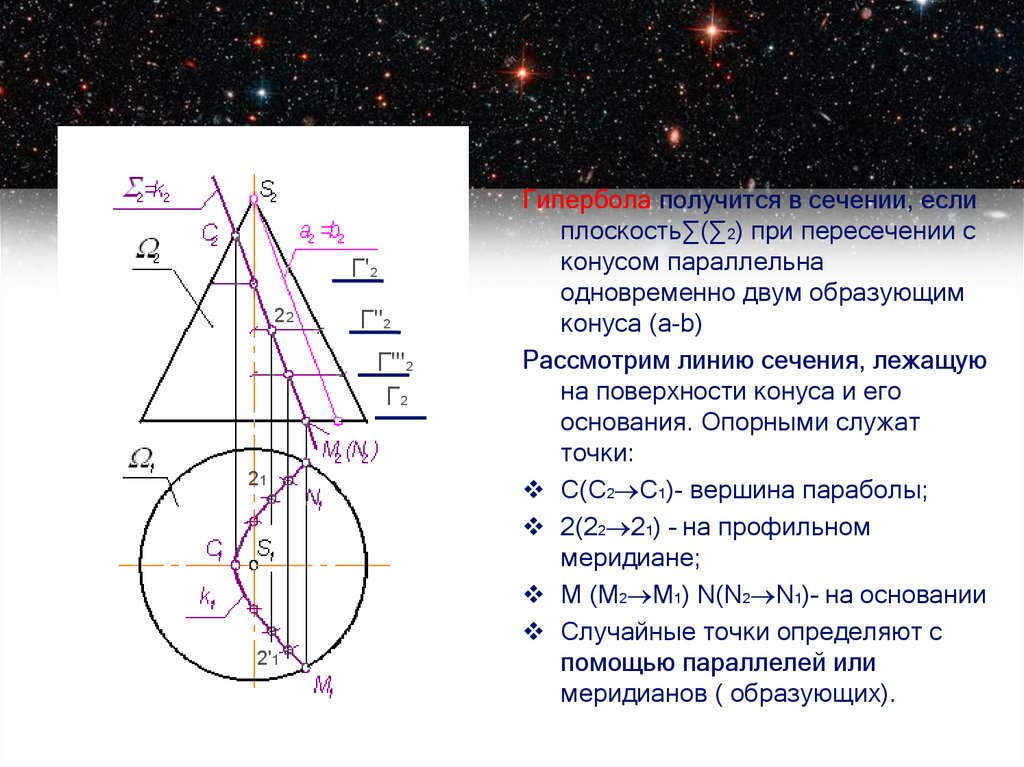
Гипербола получится в сечении, если
плоскость∑(∑2) при пересечении с
конусом параллельна
одновременно двум образующим
конуса (а-b)
Рассмотрим линию сечения, лежащую
на поверхности конуса и его
основания. Опорными служат
точки:
С(С2 С1)- вершина параболы;
2(22 21) – на профильном
меридиане;
М (М2 М1) N(N2 N1)– на основании
Случайные точки определяют с
помощью параллелей или
меридианов ( образующих).
21.
Помни!Ты всегда способен на большее!






 Инженерная графика
Инженерная графика








