Пересечение поверхности плоскостью

1. Пересечение поверхности плоскостью

2.

• Форма линии пересечения
поверхности плоскостью определяется
формой заданной поверхности и
положением плоскости относительно
этой поверхности.
• Для кривой поверхности, в общем
случае, линия пересечения - это
плоская кривая линия.
2

3.

Линию пересечения поверхности плоскостью
следует рассматривать как множество точек
пересечения секущей плоскости с линиями,
принадлежащими поверхности.
Σ∩Ф=a
Ф{m1,
m2,....,mn}
a{1,2,....,N}
1=m1 ∩ Σ
2=m2 ∩ Σ
.............
N=mn ∩ Σ

4.

Количество точек, используемых для построения линии пересечения, определяется формой поверхности и точностью построения.
Но из всего множества точек линии
пересечения обязательно должны быть
построены следующие точки:
• точки, определяющие габариты фигуру
сечения;
• точки фигуры сечения наиболее и наименее удаленные от плоскостей проекций;
• точки, определяющие видимость фигуры
сечения на проекциях.

5.

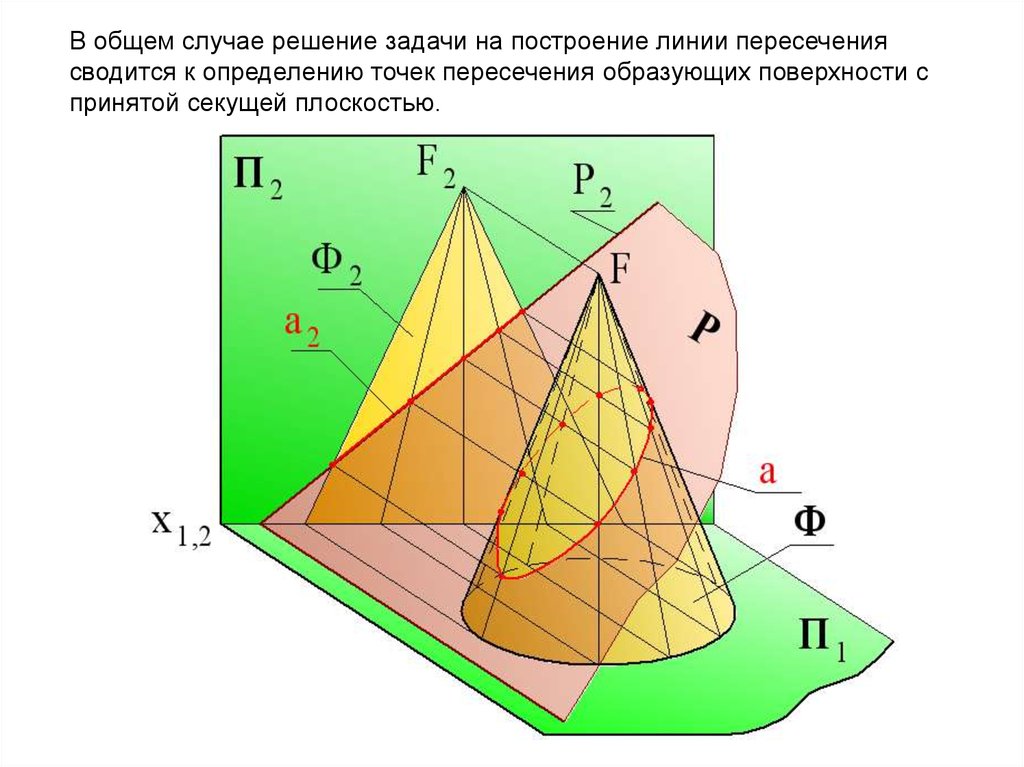
В общем случае решение задачи на построение линии пересечения
сводится к определению точек пересечения образующих поверхности с
принятой секущей плоскостью.

6.

F2
Ф2
g2 g2
1
Р2
2
72
a2
22
12
32
122
52
42
112
102
62
92
1
2
82
R
m2
4
m2
3
m2
m2
4
А2 В2
В1
m2
121 111 101 91
81
2
g1
F1
1
71
g1
11
a1
m2
21
А1
Ф1
31
41
51
61
m2
R
3
4
m2
4
2
1
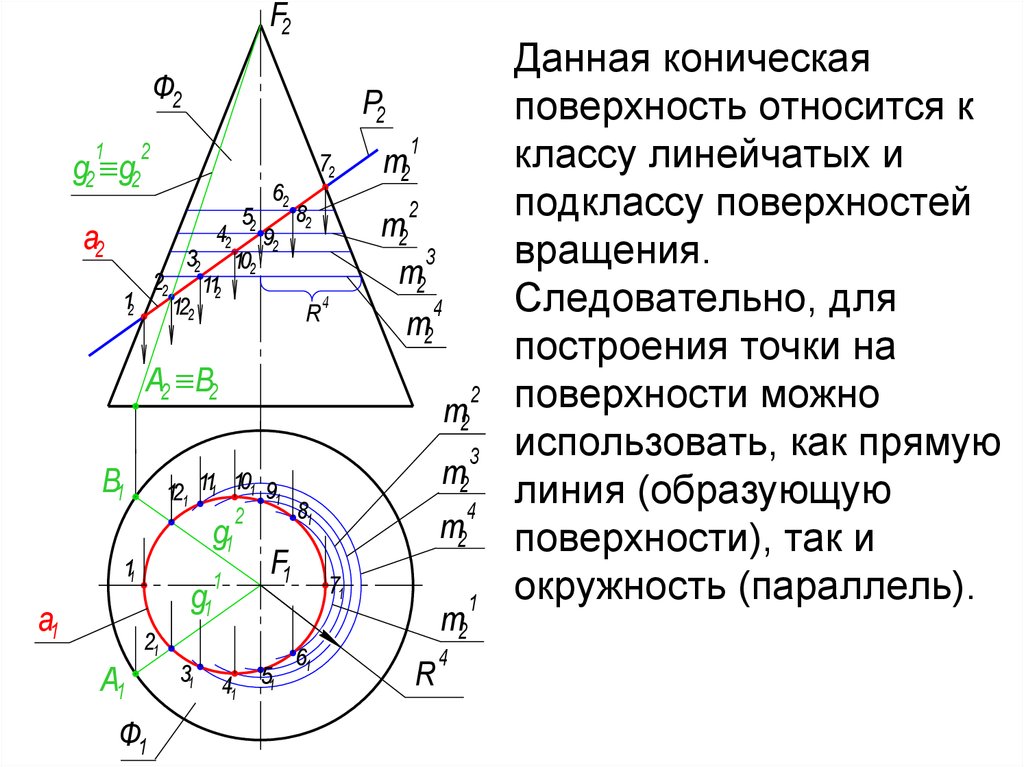
Данная коническая
поверхность относится к
классу линейчатых и
подклассу поверхностей
вращения.
Следовательно, для
построения точки на
поверхности можно
использовать, как прямую
линия (образующую
поверхности), так и
окружность (параллель).

7.

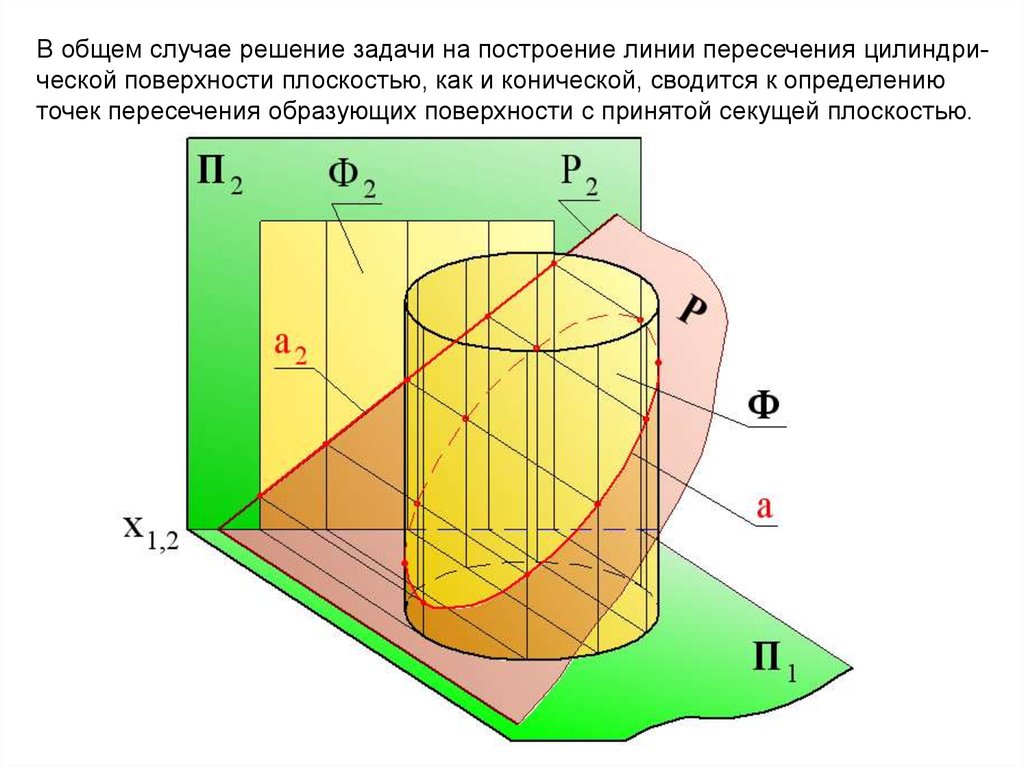
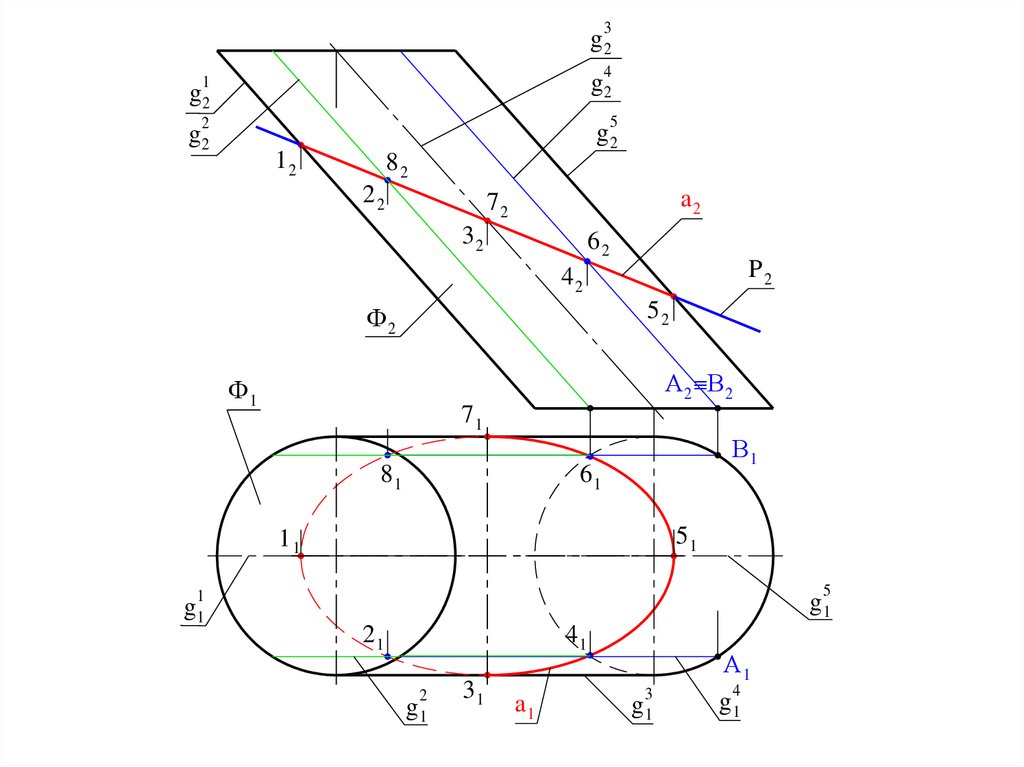
В общем случае решение задачи на построение линии пересечения цилиндрической поверхности плоскостью, как и конической, сводится к определению
точек пересечения образующих поверхности с принятой секущей плоскостью.

8.

3
g2
4
g2
1
g2
2
g2
5
g2
12
82
22
a2
72
32
62
P2
42
52
Ф2
А2 В 2
Ф1
71
81
В1
61
51
11
1
g1
5
g1
21
41
2
g1
31
a1
3
g1
А1
4
g1

9. Пересечение конической поверхности плоскостью

10.

При пересечении прямой круговой
конической поверхности плоскостью
форма линии пересечения определяется
не только формой самой поверхности, но
и положением секущей плоскости
относительно отдельных элементов
поверхности – вершины, оси вращения,
образующих.

11.

Ф – прямая круговая коническая
поверхность.
Т – секущая плоскость.
Ф ∩ Т = m,
m – линия пересечения
11

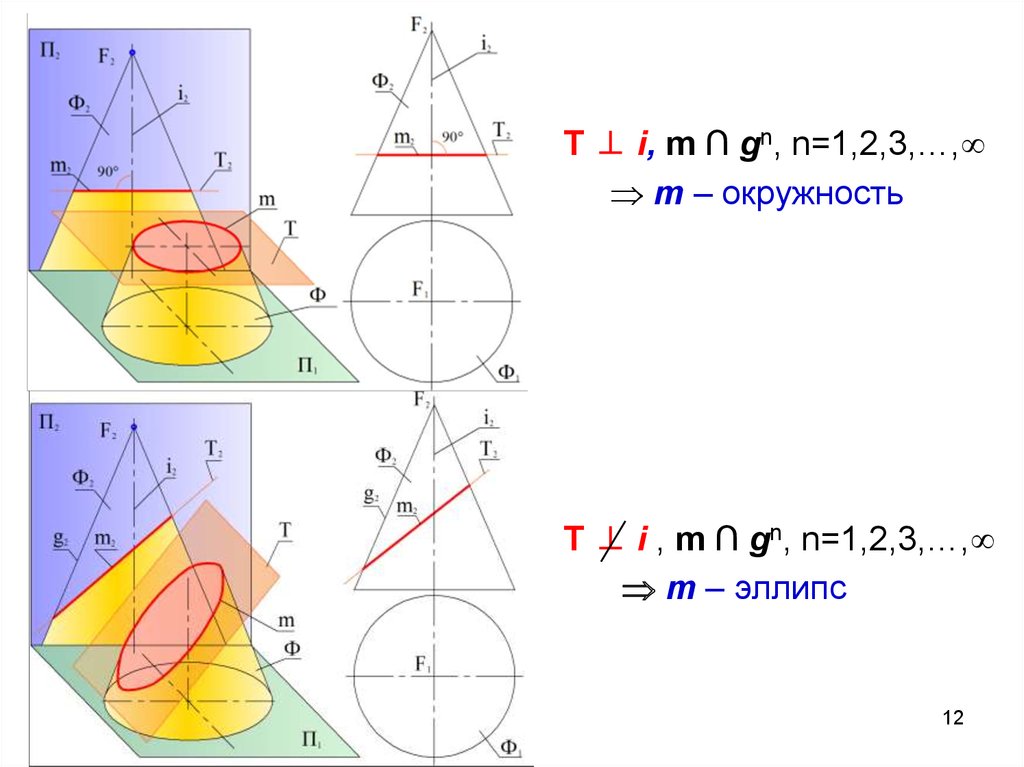
12.

T ⊥ i, m ∩ gn, n=1,2,3,…,
m – окружность
T ⊥ i , m ∩ gn, n=1,2,3,…,
m – эллипс
12

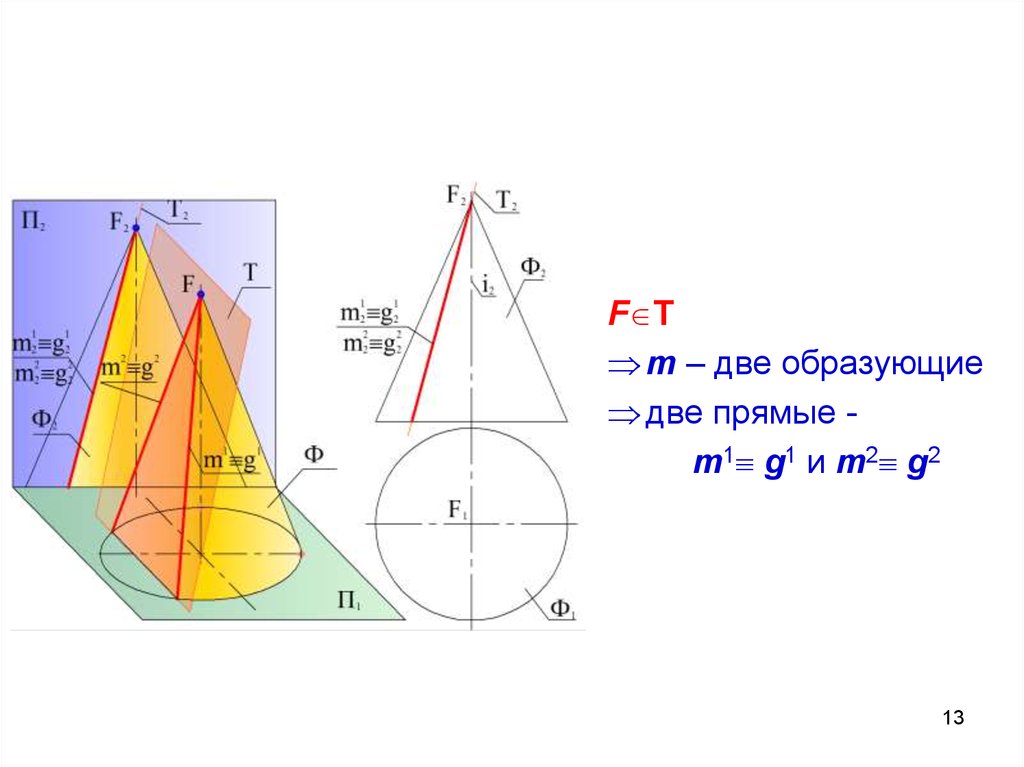
13.

F T
m – две образующие
две прямые m1 g1 и m2 g2
13

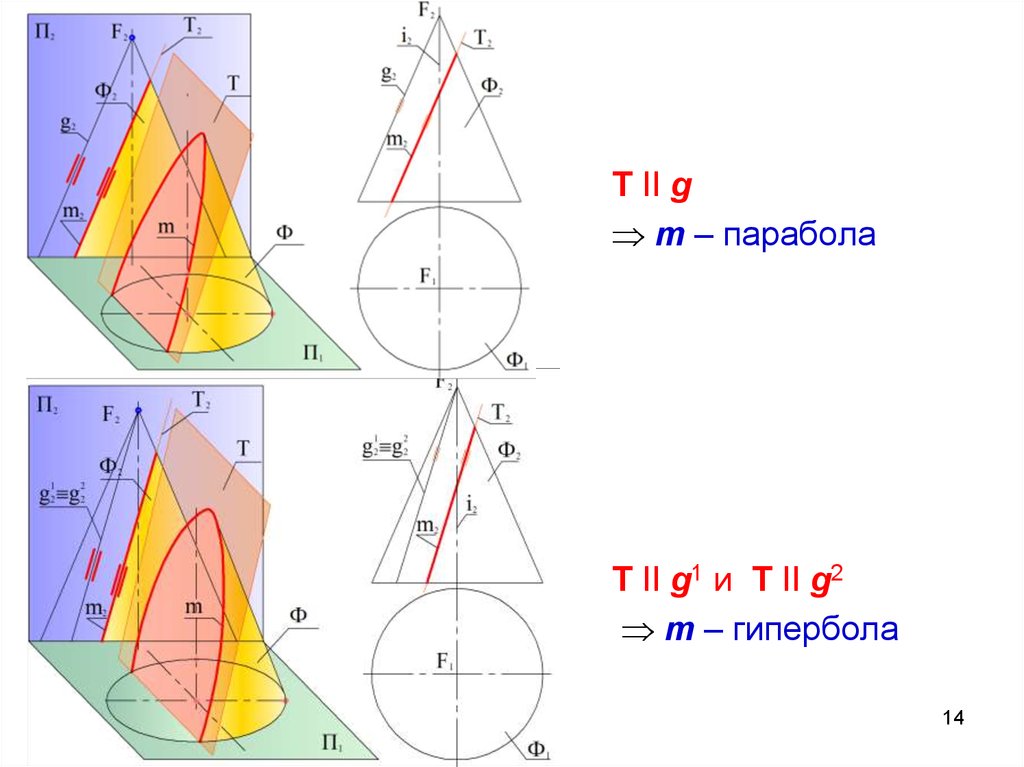
14.

T II g
m – парабола
T II g1 и T II g2
m – гипербола
14

15. Пересечение цилиндрической поверхности плоскостью

16.

Ф – прямая круговая цилиндрическая
поверхность.
Т – секущая плоскость.
Ф ∩ Т = m,
m – линия пересечения
16

17.

Форма линии пересечения прямой круговой цилиндрической поверхности плоскостью, так же как и при пересечении прямой
круговой конической поверхности, определяется положением секущей плоскости относительно отдельных элементов поверхности
– оси вращения и образующих.

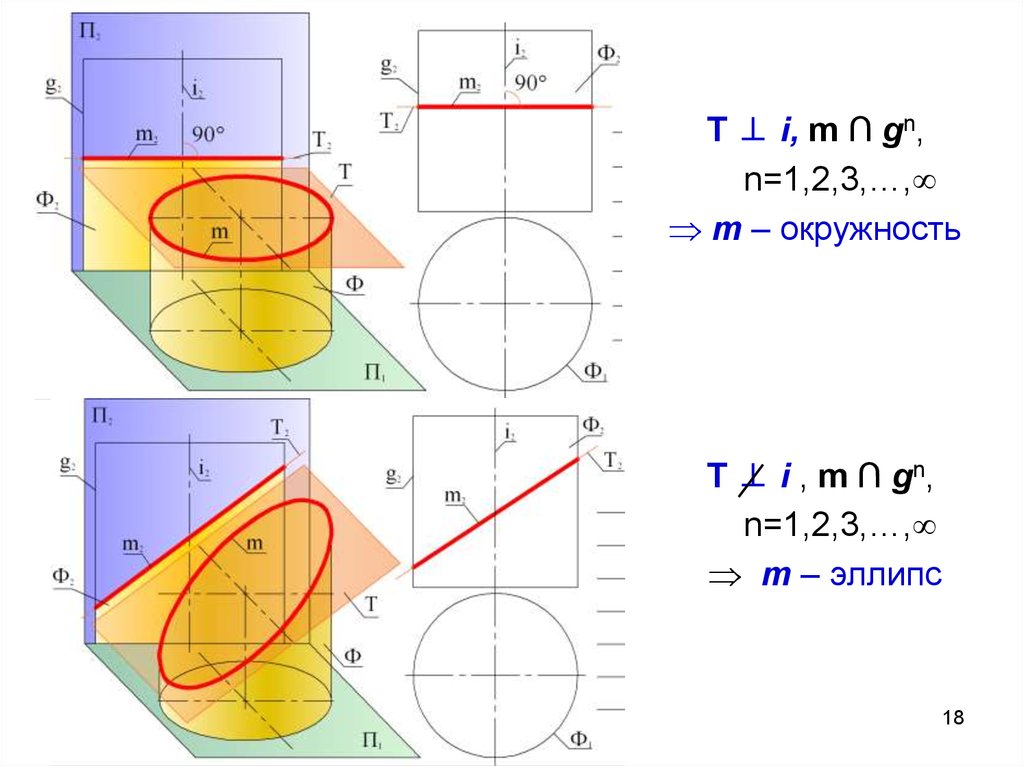
18.

T ⊥ i, m ∩ gn,
n=1,2,3,…,
m – окружность
T ⊥ i , m ∩ gn,
n=1,2,3,…,
m – эллипс
18

19.

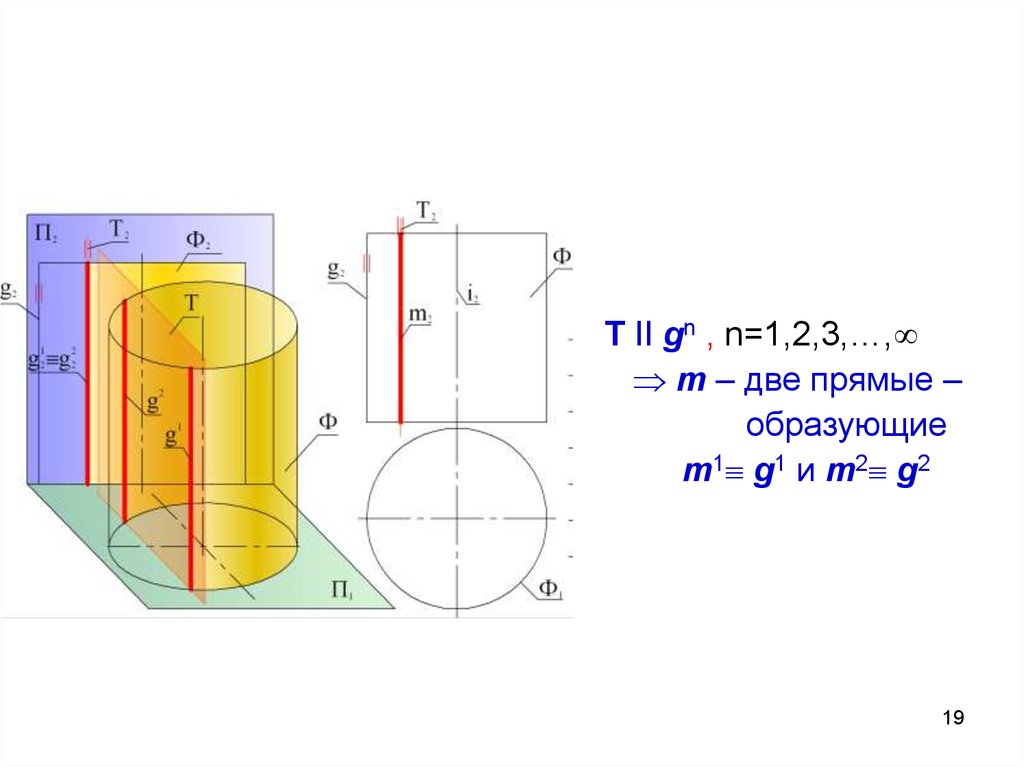
Т II gn , n=1,2,3,…,
m – две прямые –
образующие
m1 g1 и m2 g2
19

20. Пересечение гранной поверхности плоскостью

21.

• При пересечении гранной поверхности
плоскостью линия пересечения – это ломаная
линия, каждый участок которой – отрезок
прямой, представляющий собой линию
пересечения грани поверхности (отсека
плоскости) с секущей плоскостью, а точки
излома – точки пересечения ребер гранной
поверхности (отрезков прямых) с той же
секущей плоскостью.
• Следовательно, решение задачи на
построение линии пересечения сводится к
определению точек пересечения ребер гранной
поверхности с принятой секущей плоскостью.

22.

• Количество используемых точек линии
пересечения плоскости с гранной
поверхностью не является произвольно
выбираемым, как для какой-либо
кривой поверхности, а определяется
количеством ребер гранной
поверхности, пересекаемых секущей
плоскостью. Часть этих точек являются
габаритными точками и точками
перехода видимости контура фигуры
сечения на проекциях.
22

23.

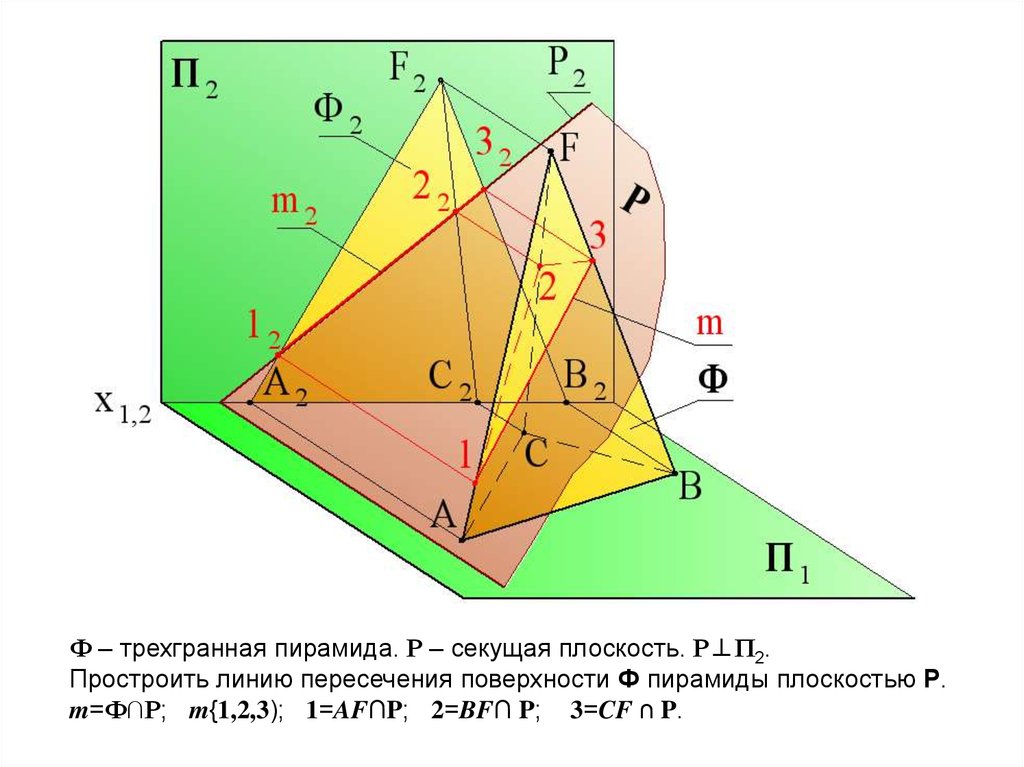
Ф – трехгранная пирамида. Р – секущая плоскость. Р⊥П2.
Простроить линию пересечения поверхности Ф пирамиды плоскостью Р.
m=Ф∩Р; m{1,2,3); 1=AF∩P; 2=BF∩ P; 3=CF ∩ P.

24.

F2
Ф2
P2
32
12
А2
11
А1
22
m2
С2
С1
21
F1
В2
31
В1
m1
Ф1
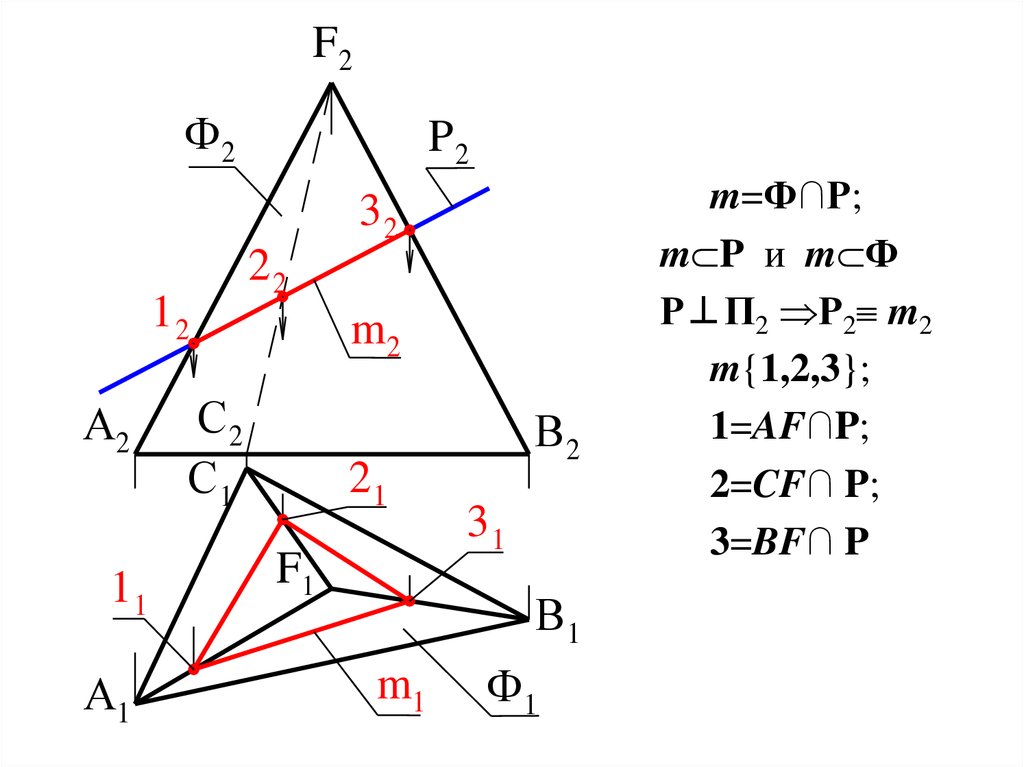
m=Ф∩Р;
m P и m Ф
Р⊥П2 Р2 m2
m{1,2,3};
1=AF∩P;
2=CF∩ P;
3=BF∩ P