Поверхности. Сечение поверхности плоскостью. Пересечение поверхностей

1. Тема. Поверхности. Сечение поверхности плоскостью. Пересечение поверхностей

Уральский федеральный университет имени первого Президента России Б.Н. Ельцина
Кафедра “Инженерная графика”
Дисциплина «Инженерная графика»
Раздел «Начертательная геометрия»
Установочная лекция 1 семестр
Тема. Поверхности.
Сечение поверхности
плоскостью. Пересечение
поверхностей
Лектор: Стриганова Л.Ю.
Установочная лекция 2.
Пересечение поверхностей.
1

2.

ПОВЕРХНОСТЬ
МНОЖЕСТВО ПОЛОЖЕНИЙ ЛИНИИ
ПЕРЕМЕЩАЮЩЕЙСЯ В ПРОСТРАНСТВЕ
ПО ОПРЕДЕЛЕННОМУ ЗАКОНУ
Установочная лекция 2. Пересечение
поверхностей. Метод секущих плоскостей
2

3. Гранные поверхности

Призма - образуется при
движении прямолинейной
образующей по ломаной
направляющей.
L – образующая,
m – направляющая
Призма прямая, если
образующие
перпендикулярны
основанию.
L2
m2
L1
m1
Призма правильная , если в
основании правильный
многоугольник
Установочная лекция 2. Пересечение поверхностей. Метод
секущих плоскостей
3

4. Гранные поверхности

Пирамида – образуется при движении
прямолинейной образующей по
ломаной направляющей.
L – образующая, m - направляющая
Все образующие имеют общую точку
(S), которая называется –
вершиной пирамиды.
Пирамида прямая, если высота
перпендикулярна основанию
S2
L2
m2
m1
S1
L1
Пирамида правильная, если в
основании правильный
многоугольник
Установочная лекция 2. Пересечение поверхностей. Метод
секущих плоскостей
4

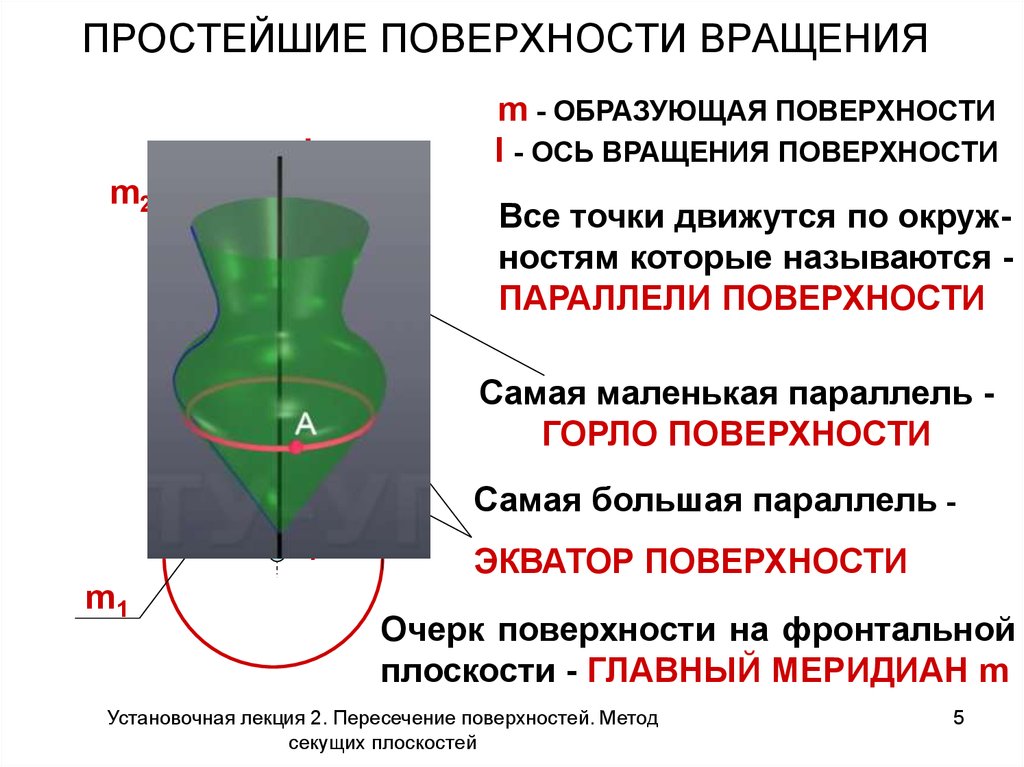
5. ПРОСТЕЙШИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ

I2
m2
m - ОБРАЗУЮЩАЯ ПОВЕРХНОСТИ
I - ОСЬ ВРАЩЕНИЯ ПОВЕРХНОСТИ
Все точки движутся по окружностям которые называются ПАРАЛЛЕЛИ ПОВЕРХНОСТИ
Самая маленькая параллель ГОРЛО ПОВЕРХНОСТИ
Самая большая параллель I1
m1
ЭКВАТОР ПОВЕРХНОСТИ
Очерк поверхности на фронтальной
плоскости - ГЛАВНЫЙ МЕРИДИАН m
Установочная лекция 2. Пересечение поверхностей. Метод
секущих плоскостей
5

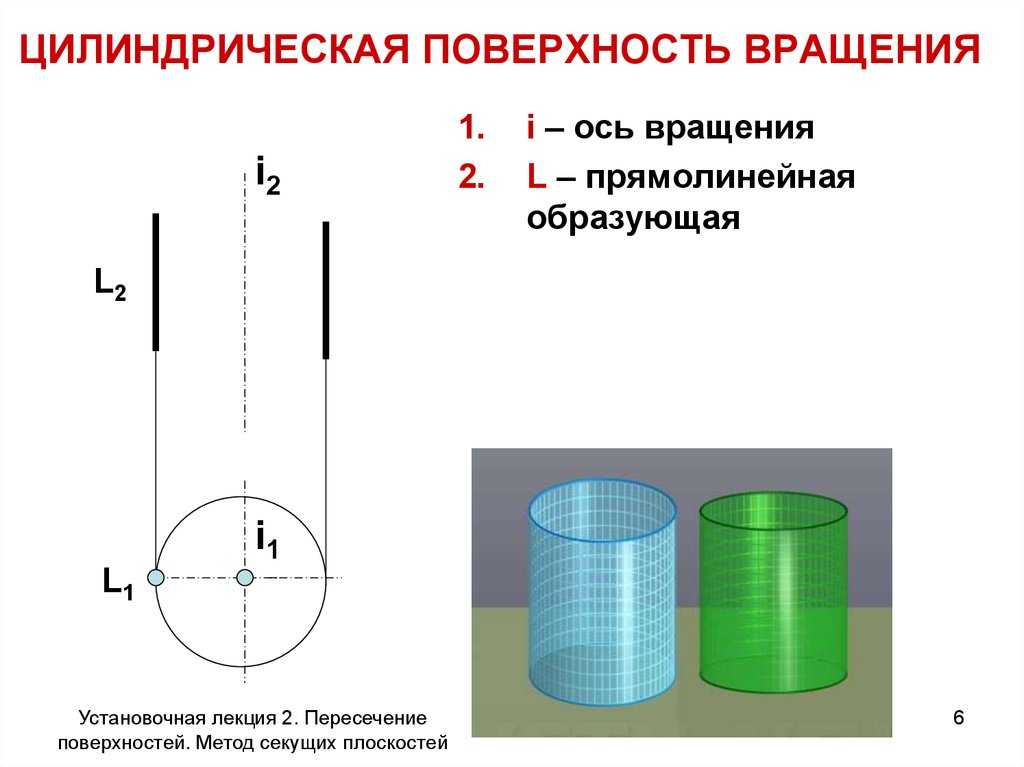
6. ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ

i2
1.
2.
i – ось вращения
L – прямолинейная
образующая
L2
i1
L1
Установочная лекция 2. Пересечение
поверхностей. Метод секущих плоскостей
6

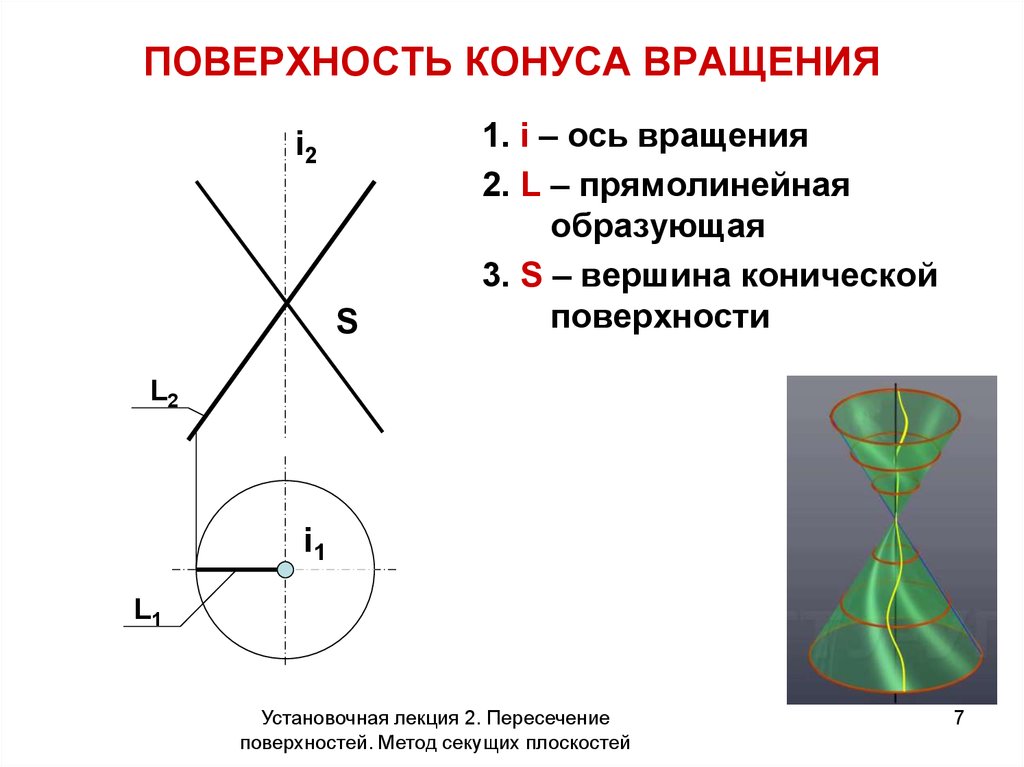
7. ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ

i2
S
1. i – ось вращения
2. L – прямолинейная
образующая
3. S – вершина конической
поверхности
L2
i1
L1
Установочная лекция 2. Пересечение
поверхностей. Метод секущих плоскостей
7

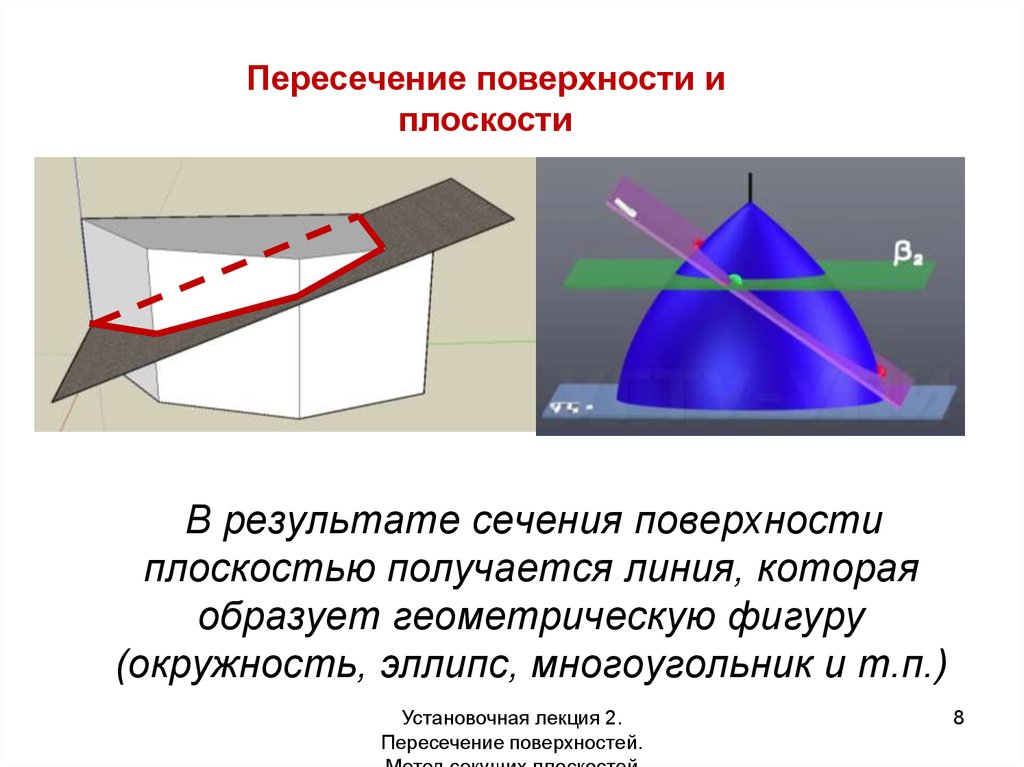
8.

Пересечение поверхности и
плоскости
В результате сечения поверхности
плоскостью получается линия, которая
образует геометрическую фигуру
(окружность, эллипс, многоугольник и т.п.)
Установочная лекция 2.
Пересечение поверхностей.
8

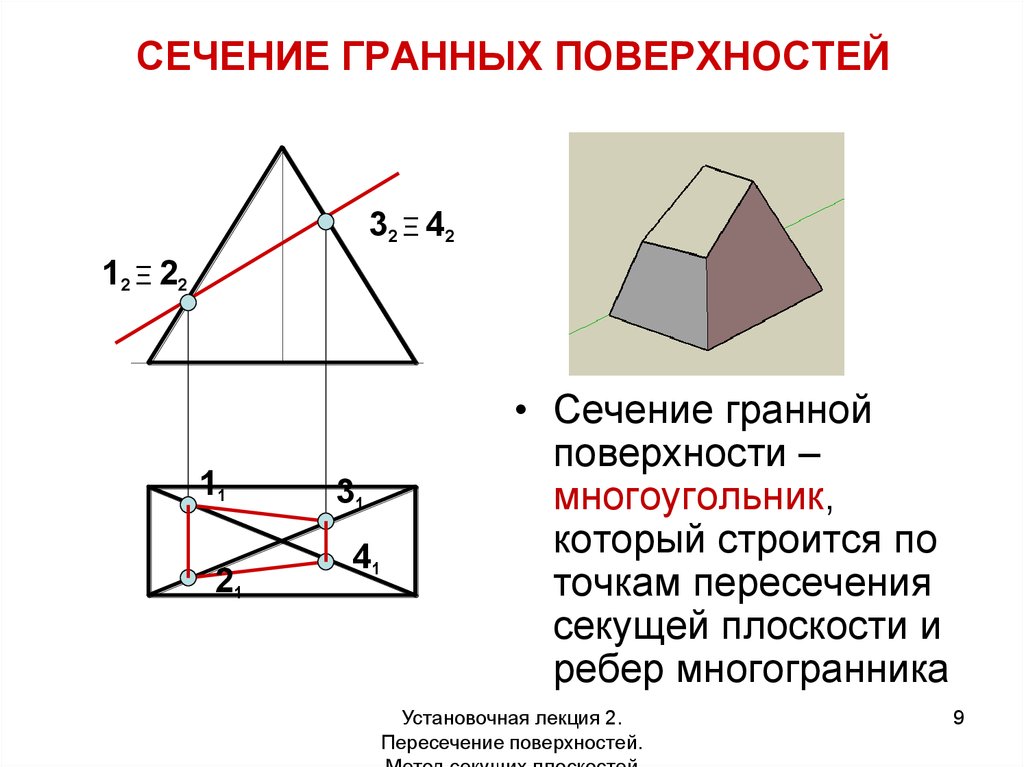
9. СЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙ

32 Ξ 42
12 Ξ 22
11
21
31
41
• Сечение гранной
поверхности –
многоугольник,
который строится по
точкам пересечения
секущей плоскости и
ребер многогранника
Установочная лекция 2.
Пересечение поверхностей.
9

10. СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ

i2
aп2
12
1. abi – окружность
2. b^ i – эллипс
22
3. g ll i - прямоугольник
L2
bп2
i1
L1
gп1
11
21
Установочная лекция 2.
Пересечение поверхностей.
10

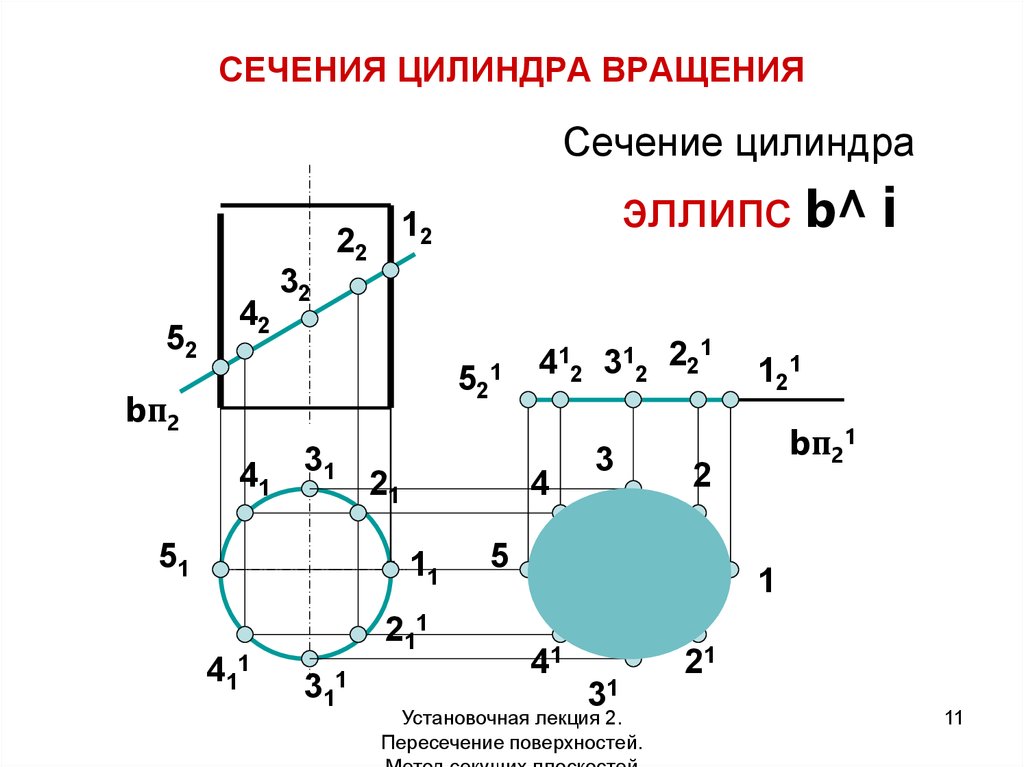
11. СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ

Сечение цилиндра
22
52
42
эллипс b^ i
12
32
521
bп2
41 31 21
51
4
11
211
411
311
1
412 312 22
3
121
bп21
2
5
1
41
31
Установочная лекция 2.
Пересечение поверхностей.
21
11

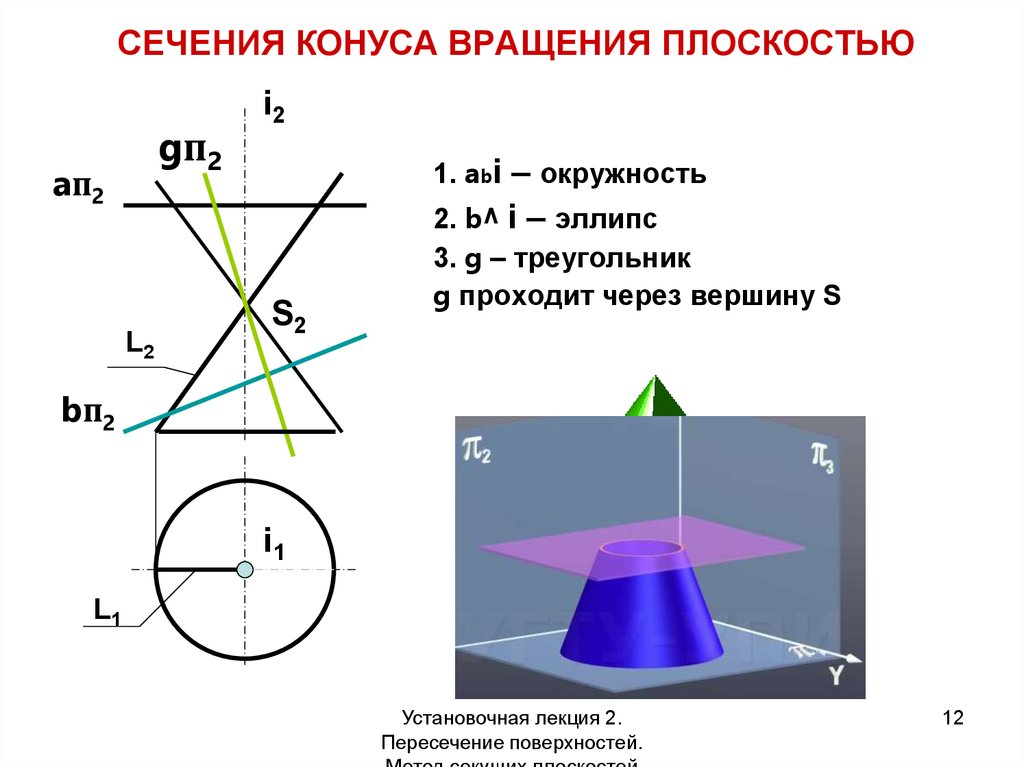
12. СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ

gп2
aп2
L2
i2
1. abi – окружность
S2
2. b^ i – эллипс
3. g – треугольник
g проходит через вершину S
bп2
i1
L1
Установочная лекция 2.
Пересечение поверхностей.
12

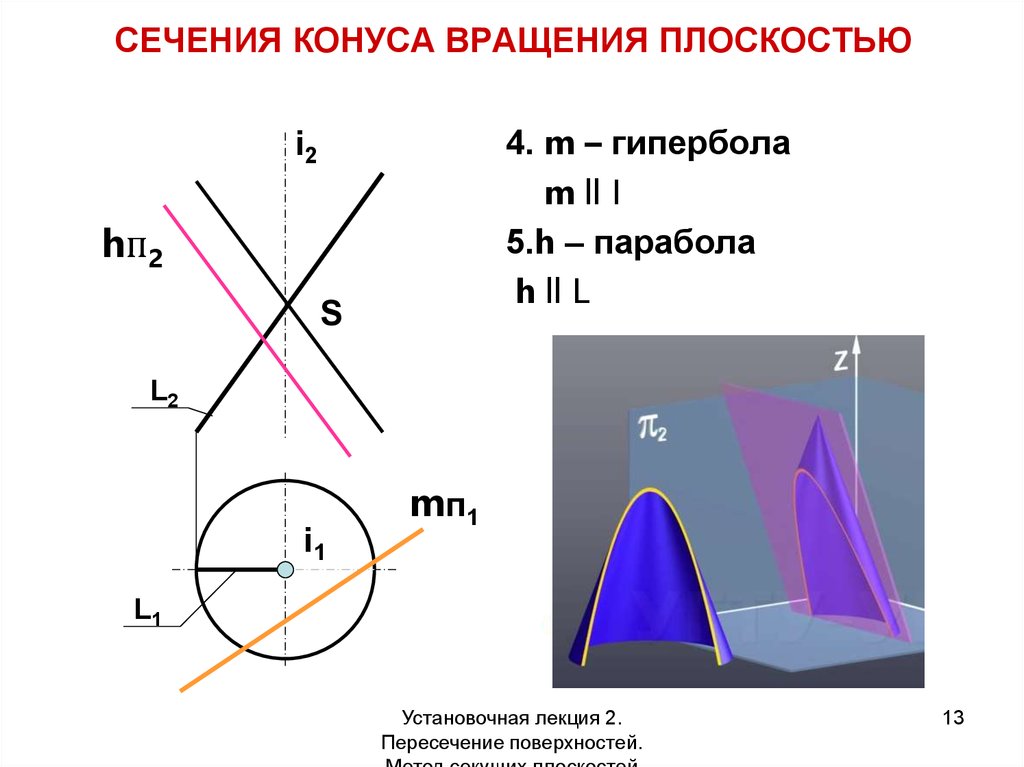
13. СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ

4. m – гипербола
m ll I
5.h – парабола
h ll L
i2
hп2
S
L2
i1
mп1
L1
Установочная лекция 2.
Пересечение поверхностей.
13

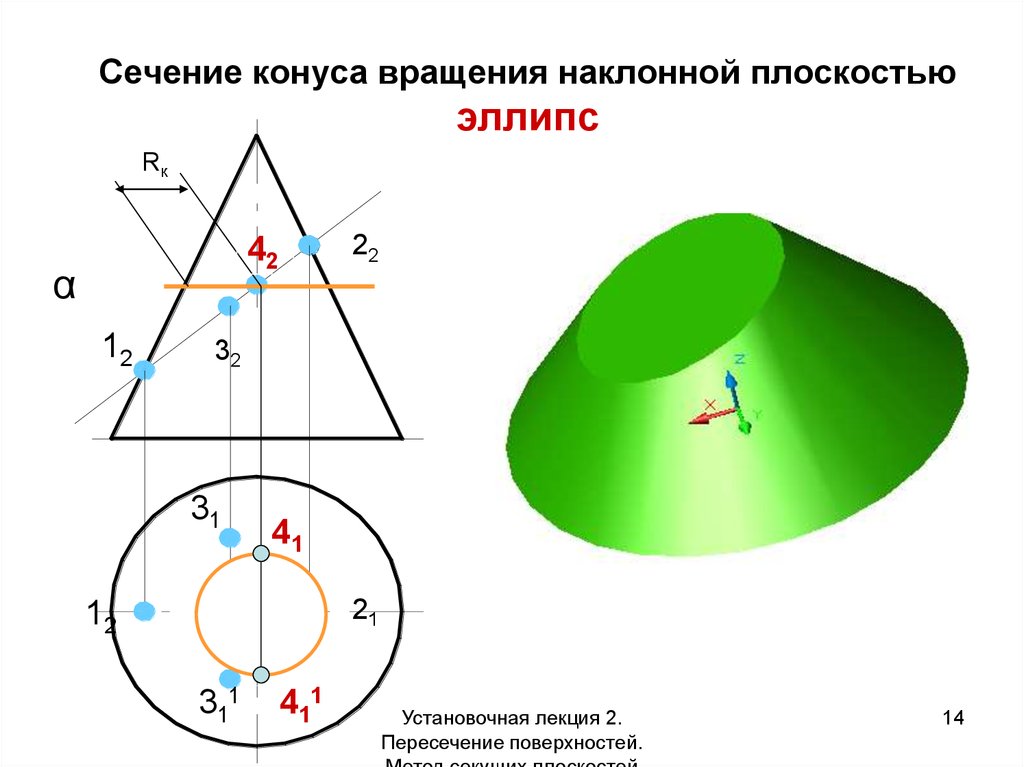
14. Сечение конуса вращения наклонной плоскостью эллипс

Rк
Rк
22
αп2
1122
22
42
3232
3311
41
1
112
2121
31111
3
411
Установочная лекция 2.
Пересечение поверхностей.
14

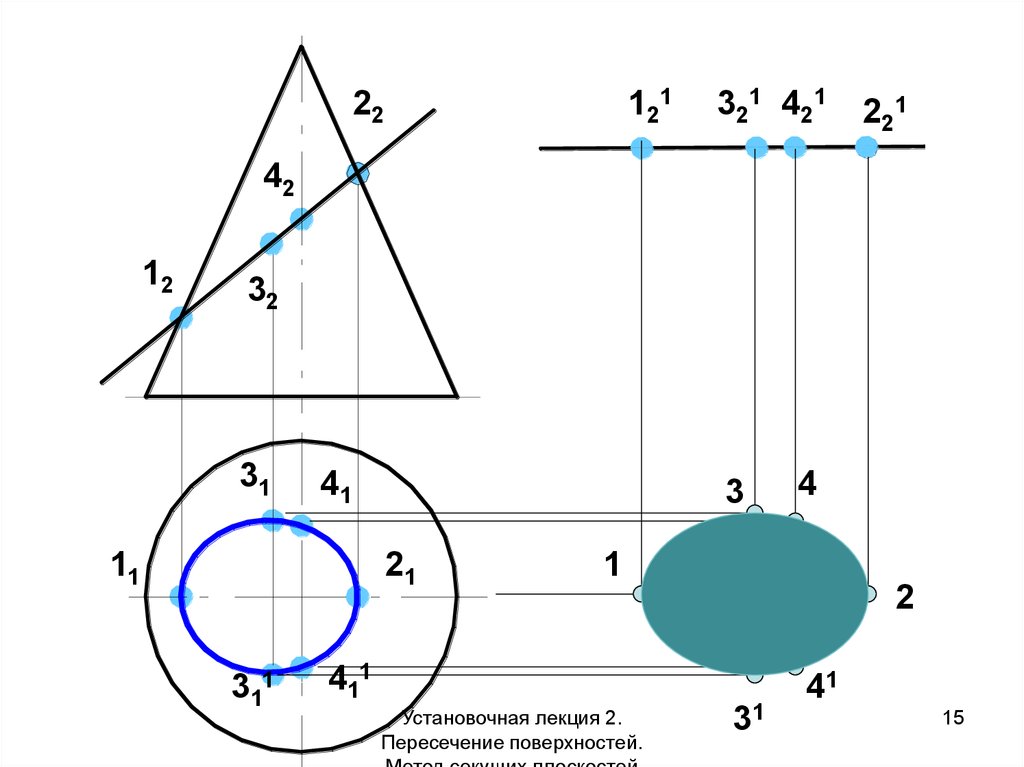
15.

121
22
321 421
221
42
12
32
31
41
11
3
21
311
4
1
2
411
Установочная лекция 2.
Пересечение поверхностей.
31
41
15

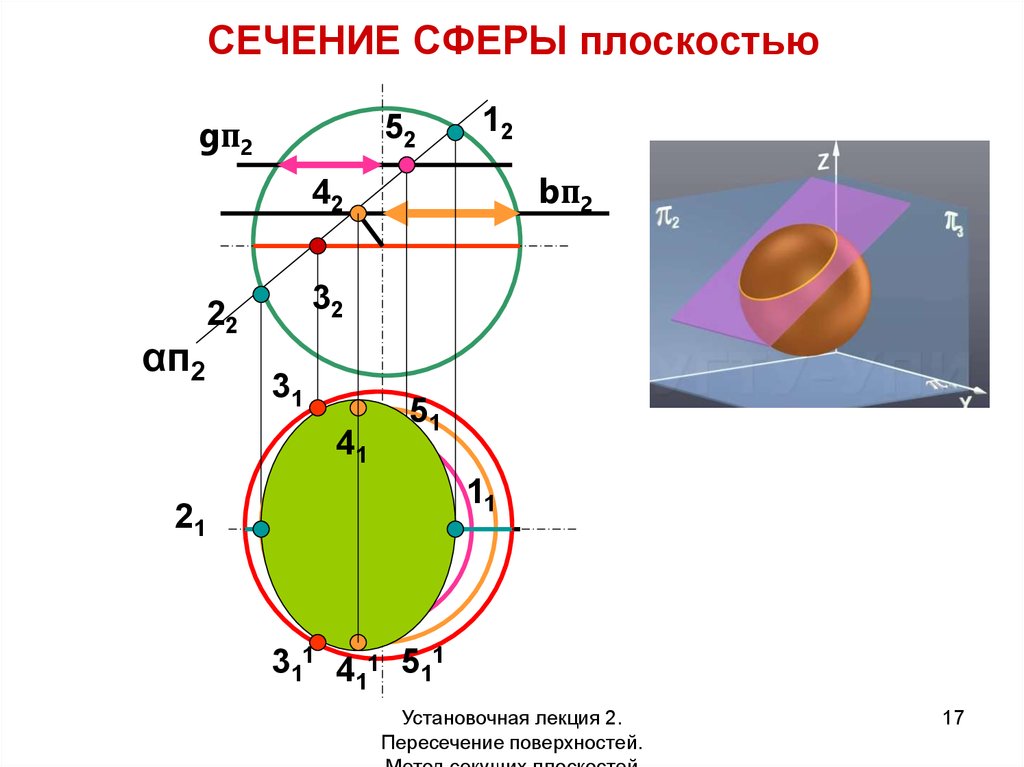
16. СЕЧЕНИЕ СФЕРЫ

Сечение сферы плоскостью – всегда
окружность, которая может проецироваться
как:
- прямая линия
- окружность
- эллипс
Установочная лекция 2.
Пересечение поверхностей.
16

17. СЕЧЕНИЕ СФЕРЫ плоскостью

gп2
52
12
bп2
42
αп2
32
22
31
41
51
11
21
311 411 511
Установочная лекция 2.
Пересечение поверхностей.
17

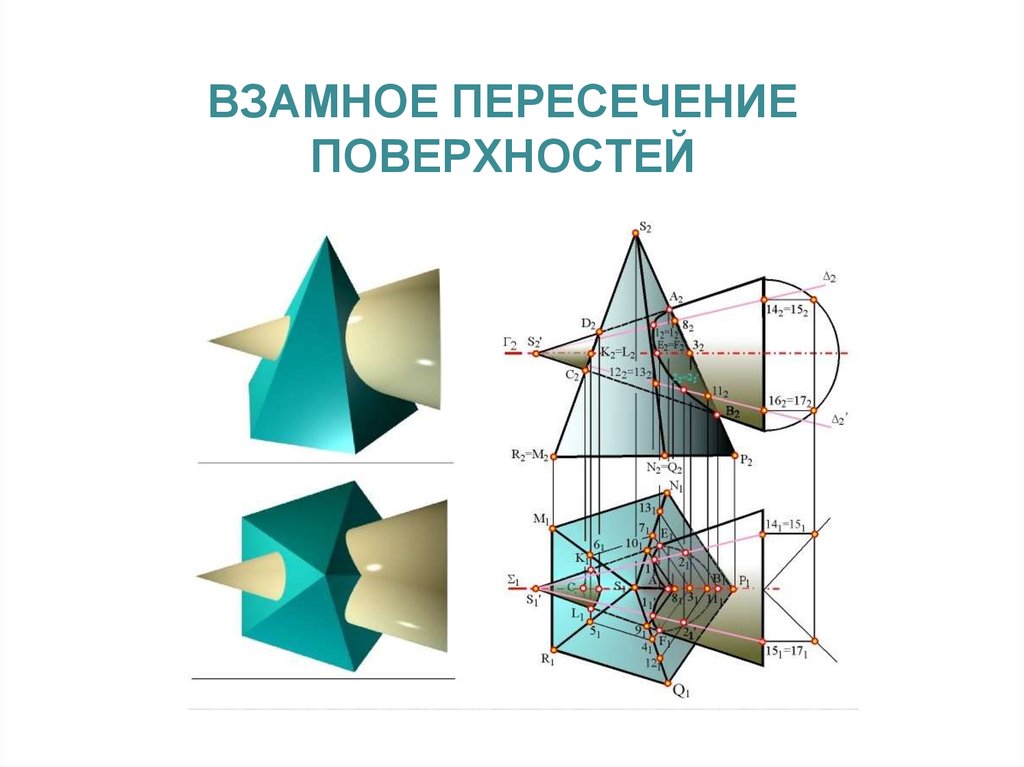
18.

ВЗАМНОЕ ПЕРЕСЕЧЕНИЕ
ПОВЕРХНОСТЕЙ

19.

Линия пересечения поверхностей -
совокупность точек одновременно
принадлежащих двум
пересекающимся поверхностям
Установочная лекция 2.
Пересечение поверхностей.
19

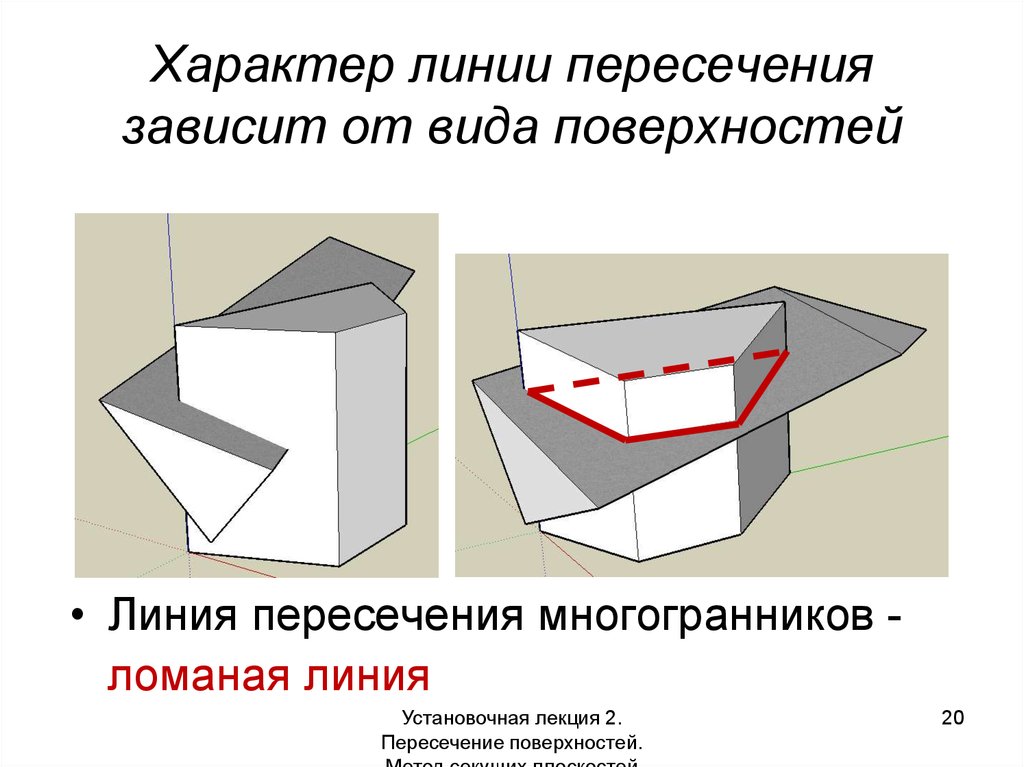
20. Характер линии пересечения зависит от вида поверхностей

• Линия пересечения многогранников ломаная линия
Установочная лекция 2.
Пересечение поверхностей.
20

21.

Линия пересечения
многогранника и
поверхности вращения сочетание плоских кривых
линий (парабола,
гипербола, эллипс и т.д.)
Линия пересечения двух
поверхностей второго
порядка пространственная
кривая
Установочная лекция 2.
Пересечение поверхностей.
21

22.

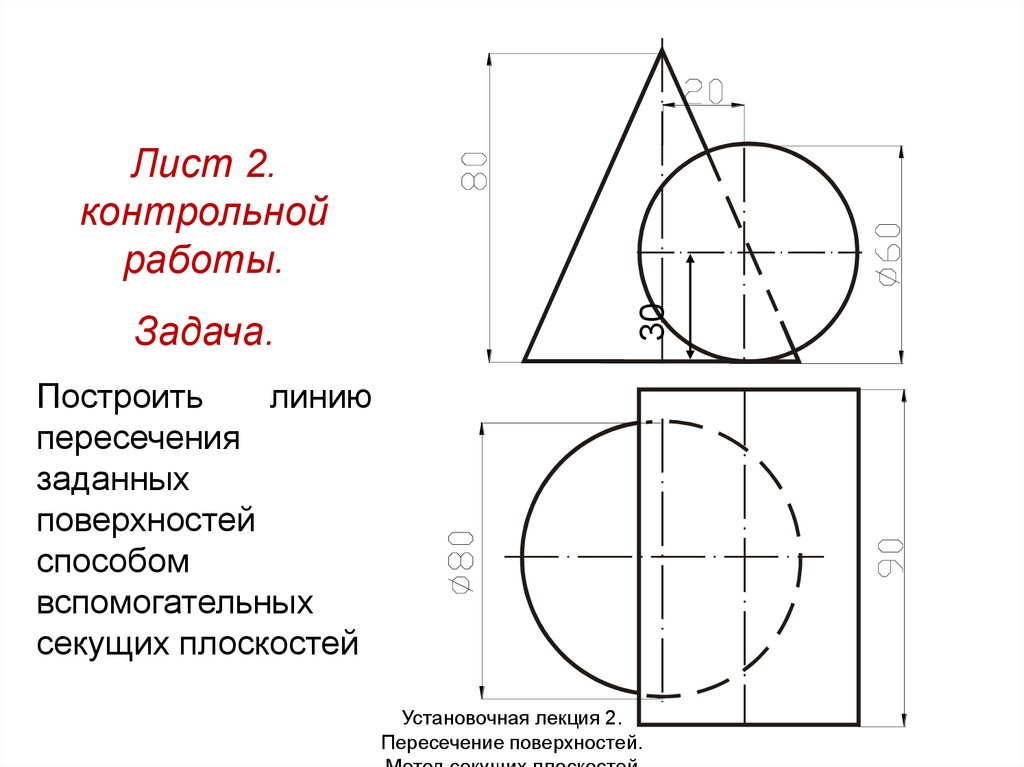
Задача.
30
Лист 2.
контрольной
работы.
Построить
линию
пересечения
заданных
поверхностей
способом
вспомогательных
секущих плоскостей
Установочная лекция 2.
Пересечение поверхностей.
22

23.

1. Провести анализ изображения
пересекающихся поверхностей
Установочная лекция 2.
Пересечение поверхностей.
23

24.

Цилиндр является
фронтально
проецирующей
поверхностью, так как
все его образующие
фронтально
проецирующие
прямые
Линия пересечения
заданных
поверхностей на
фронтальной
плоскости совпадает
с очерком цилиндра
Установочная лекция 2.
Пересечение поверхностей.
24

25.

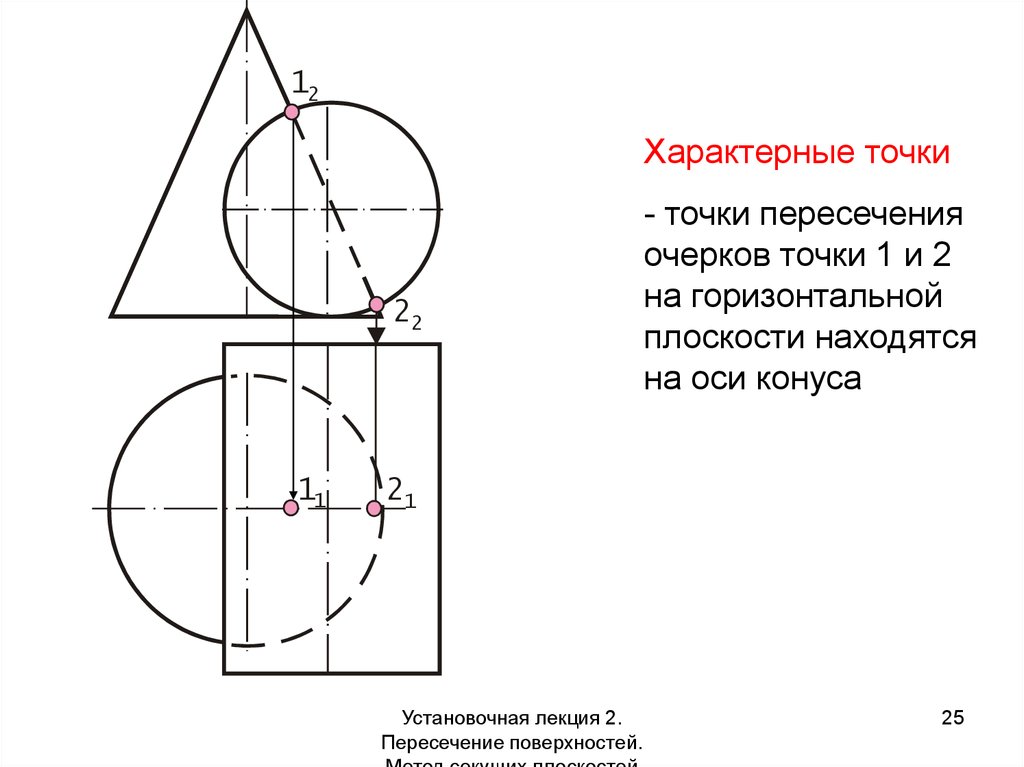
12
Характерные точки
22
11
- точки пересечения
очерков точки 1 и 2
на горизонтальной
плоскости находятся
на оси конуса
21
Установочная лекция 2.
Пересечение поверхностей.
25

26.

12
Характерные точки
- низшие точки
очерка цилиндра
12
9 и 10 лежат на
основании конуса
12
22
11
22
11
21
22
21
92Ξ102
91
12
22
11
21
11
21
лекция 2.
10Установочная
1
Пересечение поверхностей.
26

27.

12
π2
52Ξ62
12
22
11
21
22
92Ξ102
91
12
22
11
21
11
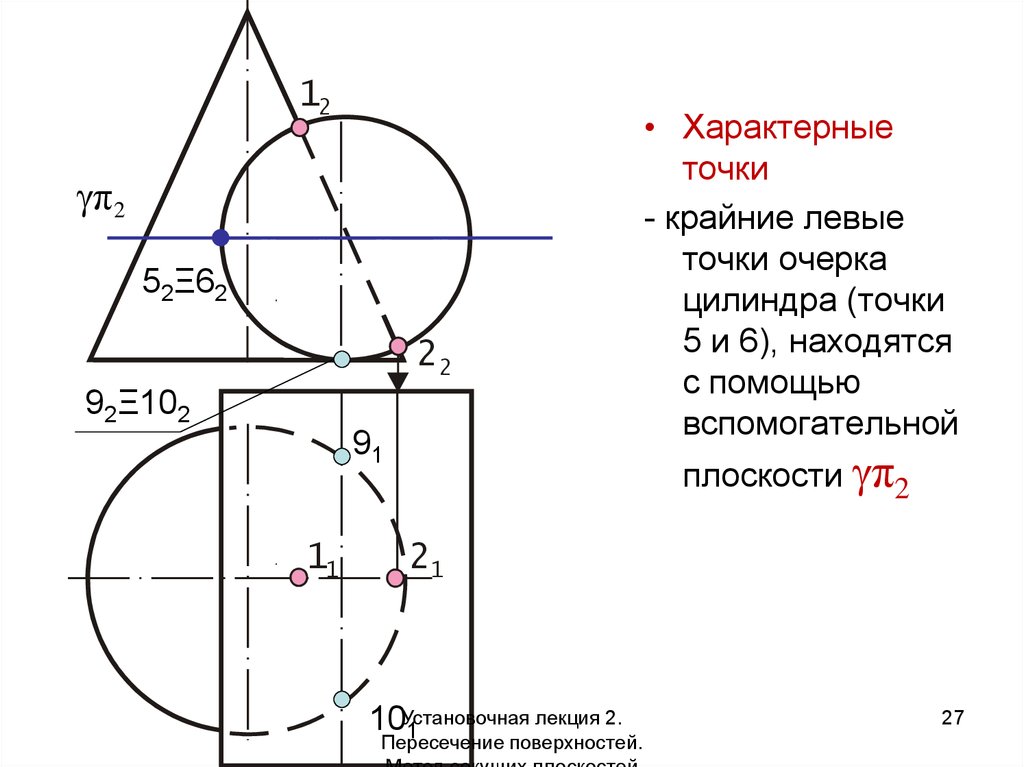
• Характерные
точки
- крайние левые
точки очерка
цилиндра (точки
5 и 6), находятся
с помощью
вспомогательной
плоскости π2
21
лекция 2.
10Установочная
1
Пересечение поверхностей.
27

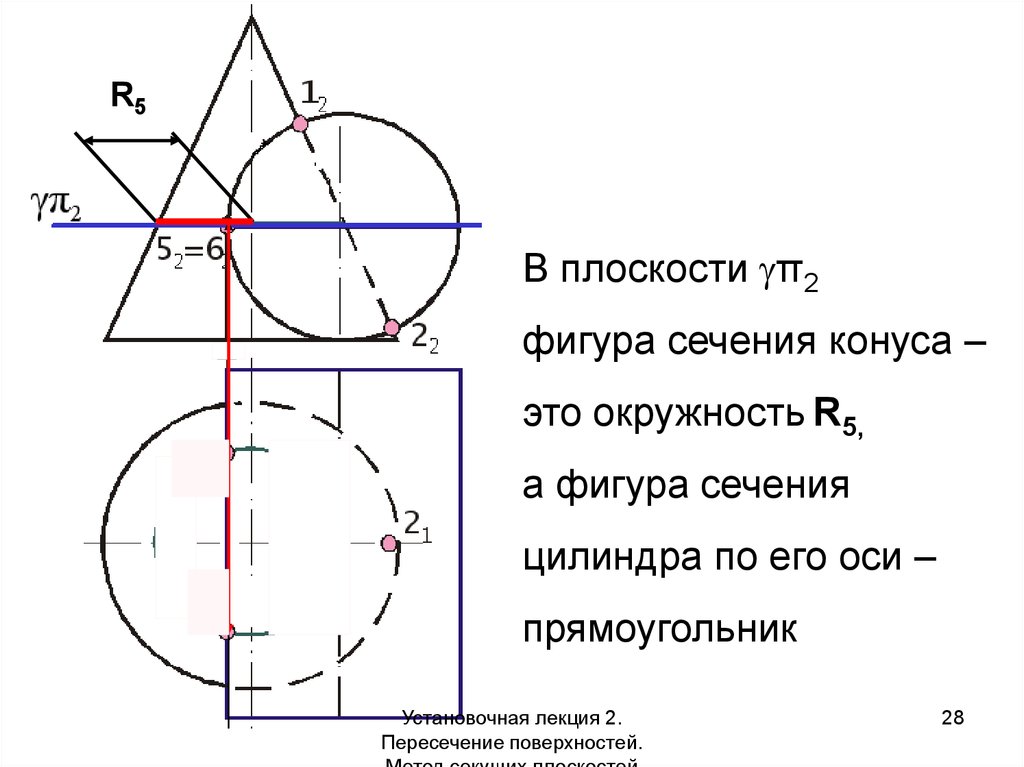
28.

R5
В плоскости π2
фигура сечения конуса –
это окружность R5,
а фигура сечения
цилиндра по его оси –
прямоугольник
Установочная лекция 2.
Пересечение поверхностей.
28

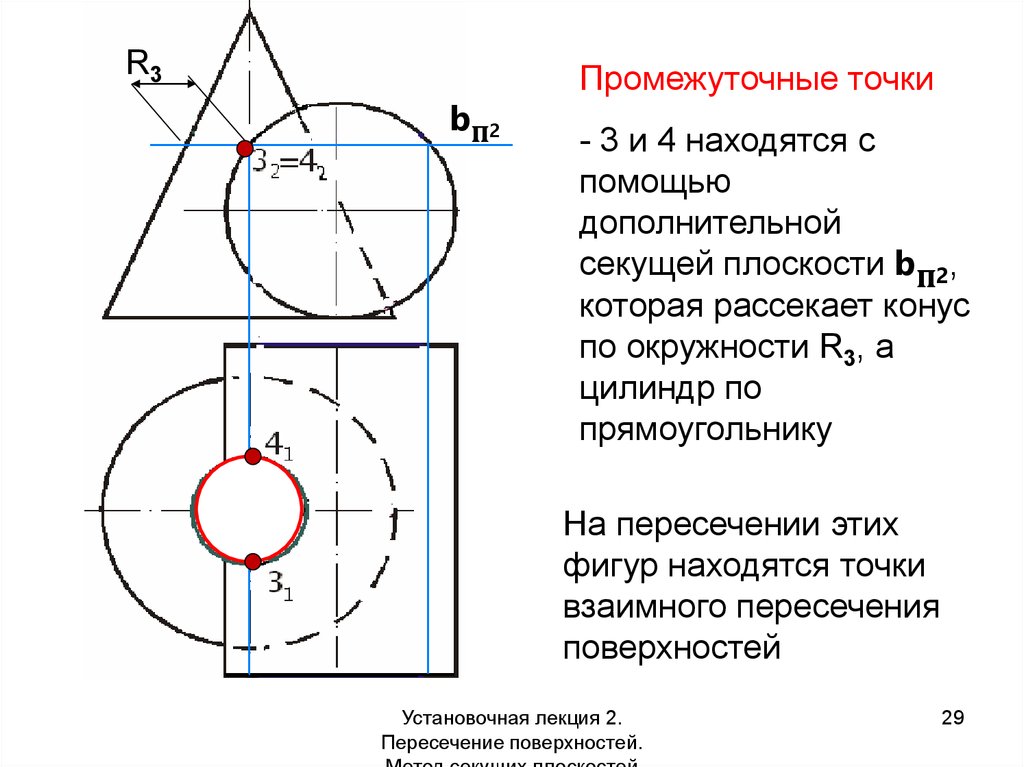
29.

R3
bп2
Промежуточные точки
- 3 и 4 находятся с
помощью
дополнительной
секущей плоскости bп2,
которая рассекает конус
по окружности R3, а
цилиндр по
прямоугольнику
На пересечении этих
фигур находятся точки
взаимного пересечения
поверхностей
Установочная лекция 2.
Пересечение поверхностей.
29

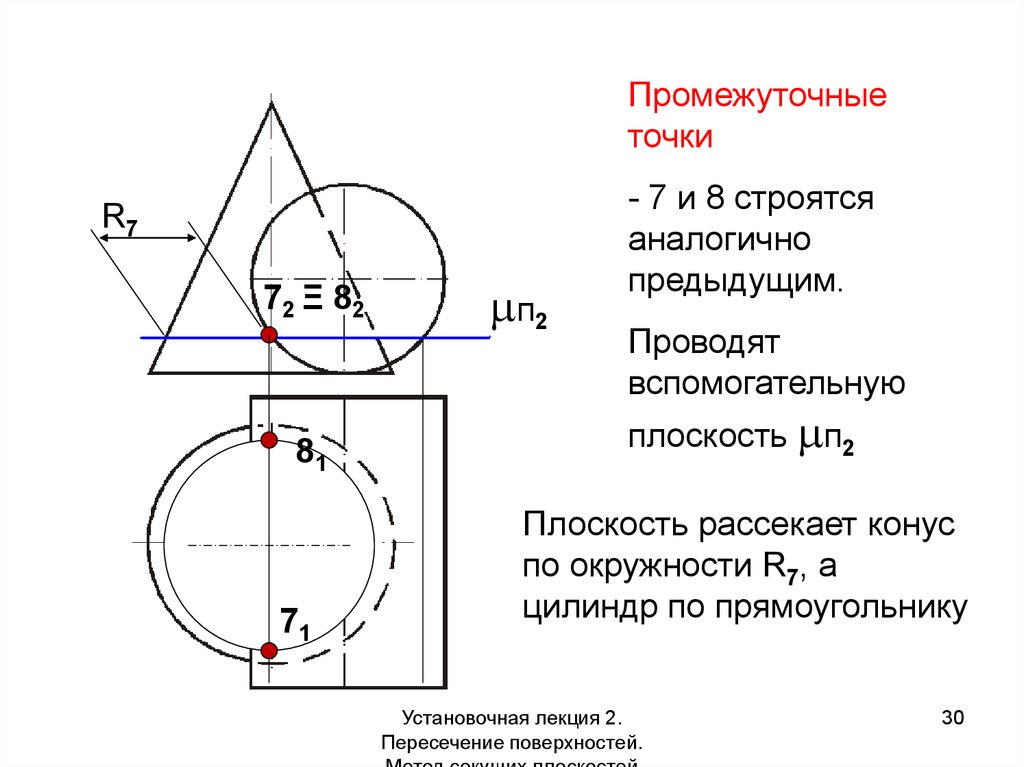
30.

Промежуточные
точки
R7
72 Ξ 82
81
71
п2
- 7 и 8 строятся
аналогично
предыдущим.
Проводят
вспомогательную
плоскость п2
Плоскость рассекает конус
по окружности R7, а
цилиндр по прямоугольнику
Установочная лекция 2.
Пересечение поверхностей.
30

31.

Соединяют полученные
точки в последовательности,
как на проецирующей
поверхности конуса:
1,3,5,7,9,2,10,8,6,4,1
Обводят
изображение с
учетом видимости
Установочная лекция 2.
Пересечение поверхностей.
31

32. Выводы по теме

• Геометрические фигуры сечений
поверхностей строят с помощью метода
вспомогательных секущих плоскостей
• Секущие плоскости – посредники
должны занимать частное положение
• Взаимное пересечение поверхностей –
линии принадлежащие двум
поверхностям одновременно
Установочная лекция 2.
Пересечение поверхностей.
32

33. Рекомендованная литература

• Бударин О. С. Начертательная геометрия. Краткий
курс: учеб. пособие для студентов вузов,
обучающихся по направлениям в обл. техники и
технологий / О. С. Бударин. - 2-е изд., испр. - СанктПетербург ; Москва ; Краснодар: Лань, 2009. - 368 с.
• Королев Ю. И. Начертательная геометрия: учеб. для
вузов инженер.-техн. специальностей / Ю. И.
Королев. - 2-е изд. - Москва ; Санкт-Петербург ;
Нижний Новгород [и др.]: Питер, 2010. - 256 с.
• Чекмарев А. А. Начертательная геометрия и
черчение: учеб. для студентов вузов, обучающихся
по техн. специальностям / А. А. Чекмарев. - 3-е изд.,
перераб. и доп. - Москва: Юрайт, 2011. - 471 с.
Установочная лекция 2. Пересечение
поверхностей. Метод секущих плоскостей
33

34. Благодарю за внимание

Установочная лекция 2. Пересечение
поверхностей. Метод секущих плоскостей
34