01-формула суммы н членов арифмет прогрессии

1.

2.

Арифметическая прогрессия
Определение: арифметической прогрессией называется
последовательность, каждый член которой, начиная со второго,
равен предыдущему члену, сложенному с одним и тем же числом.
Это число называется разностью арифметической прогрессии.
Таким образом, если числовая последовательность {аn} есть
арифметическая прогрессия, то для нее существует такое число dразность арифметической прогрессии, что аn+1 = аn + d для любого
натурального чиста n.
При d > 0 арифметическая прогрессия является возрастающей
последовательностью, при d < 0 – убывающей
последовательностью, при d=0 все члены арифметической
прогрессии равны а1.

3.

Из определения арифметической прогрессии
следует, что
а2 = а1 +d
а3 = а2 +d = (а1 +d)+d= а1 +2d
а4 = а3 +d = (а1 +2d)+d= а1 +3d
Чтобы найти аn , надо к аn-1 прибавить произведение
(n-1)*d, то есть
аn = а1 + (n-1)*d
Это формула n-ого члена арифметической
прогрессии.

4.

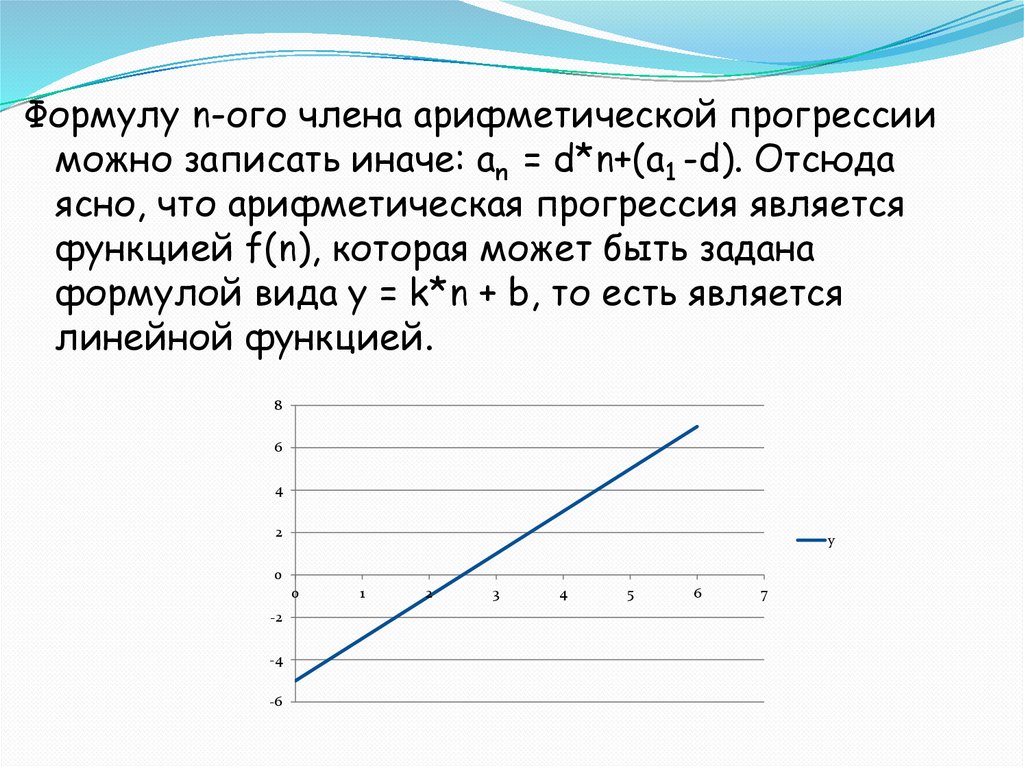
Формулу n-ого члена арифметической прогрессии
можно записать иначе: аn = d*n+(а1 -d). Отсюда
ясно, что арифметическая прогрессия является
функцией f(n), которая может быть задана
формулой вида у = k*n + b, то есть является
линейной функцией.
8
6
4
2
y
0
0
-2
-4
-6
1
2
3
4
5
6
7

5.

Характеристическое свойство
арифметической прогрессии
Каждый член арифметической прогрессии, начиная
со второго ,равен средним арифметическим между
предыдущим и последующим членом.
an 1 an 1
an
2
Верно и обратное: числовая последовательность
является арифметической прогрессия тогда и
только тогда, когда каждый ее член начиная со
второго, есть среднее арифметическое
предыдущего и последующего члена.

6.

Сумма n первых членов
арифметической прогрессии
Если арифметическая прогрессия содержит n членов,
то ее сумму можно вычислить по формуле
a1 a n
Sn
*n
2
или
2a1 d * (n 1)
Sn
*n
2

7.

Отдыхающий, следую совету врача, загорал в первый
день 5 минут, а в каждый следующий день увеличивал
время пребывания на солнце на 5 мин. В какой день
недели время его пребывания на солнце будет равно 40
минут, если он начал загорать в среду.
Решение.
Время пребывания на солнце отдыхающего составляет
арифметическую прогрессию, в которой первый член
равен 5, разность равно тоже 5, аn = 40.Найдем n.
an = а1 + (n-1)*d
40=5+(n-1)*5
n=8
Если а 1 – среда, то а 8 – тоже среда
Ответ: в среду.

8.

Известно, что внутренние углы некоторого выпуклого многоугольника,
наименьший угол которого равен 120 0,образуют арифметическую
прогрессию с разностью 5 0. Определите число сторон этого
многоугольника.
Решение.
а1 = 120; d = 5.
Известно , что сумма внутренних углов выпуклого многоугольника равна
180*(n-2). По условию задачи внутренние углы выпуклого
многоугольника образуют арифметическую прогрессию, значит, Sn –
сумма n первых членов этой прогрессии – сумма внутренних углов этого
многоугольника.
Составим и решим уравнение:
240 5(n 1)
* n 180 * (n 2)
2
n 2-25n+144=0
n1 =16
n2 =9
При n1 =16 наибольший угол а16 =120 +15*5=195 0, больше развернутого, что
противоречит условию задачи (многоугольник - выпуклый)
Ответ: 9.

9.

В классе:
№16.30,16.32,16.33,16.34,16.35, 16.36