Похожие презентации:
Множественная регрессия
1. Множественная регрессия
Лекция2. Цели лекции
Обобщение парной регрессии наслучай нескольких объясняющих
переменных
Интерпретация множественной
регрессии
Качество множественной регрессии
Новые возможности регрессии
2
3. Виды множественной регрессии
1. Классическая линейная регрессия2. Нелинейная регрессия
3. Специальные виды переменных
3
4. Модель множественной регрессии
Множественная регрессия имеет вид:M [Y / x1, x2 , , xm ] f ( x1, x2 , , xm )
Уравнение множественной регрессии:
Y f ( , X)
где X = (X1, X2, , Xm) вектор объясняющих переменных,
вектор параметров (подлежащих определению),
вектор случайных ошибок (отклонений),
Y зависимая переменная.
4
5. Линейная модель множественной регрессии
Теоретическое уравнение линейной множественнойрегрессии:
Y 0 1 X 1 2 X 2 m X m
или для индивидуальных наблюдений:
yi 0 1 xi1 2 xi 2 m xim i
i = 1, 2, , n, n m+1, k = n m 1 число степеней свободы
Для обеспечения статистической надежности должно
выполняться условие: n 3( m 1)
5
6. Оценки параметров линейной множественной регрессии
Эмпирическое уравнение регрессии:Y b0 b1 X 1 ... bm X m
y i b0 b1 xi1 ... bm xim
Самый распространенный метод оценки параметров – МНК
2
n
b j , j 0, m : yi (b0 b j xij ) ei2 min
i 1
j 1
i 1
n
m
yi
6
7. Предпосылки МНК
1 . M i 0, i 1,2,..., n0
2 . D i D j , i, j
0
2
0, i j
3 . Cov( i , j ) 2
, i j
0
Гомоскедастичность
Отсутствие автокорреляции
40. Cov i , xi 0
50. Модель является линейной относительно параметров
7
8. Дополнительные предпосылки МНК
60. Отсутствие мультиколлинеарности: междуобъясняющими переменными отсутствует строгая
(сильная) линейная зависимость
70. Ошибки i имеют нормальное распределение:
i N (0, )
2
При выполнении этих предпосылок МНК-оценки
коэффициентов множественной регрессии будут
несмещенными, состоятельными и эффективными в классе
линейных оценок
8
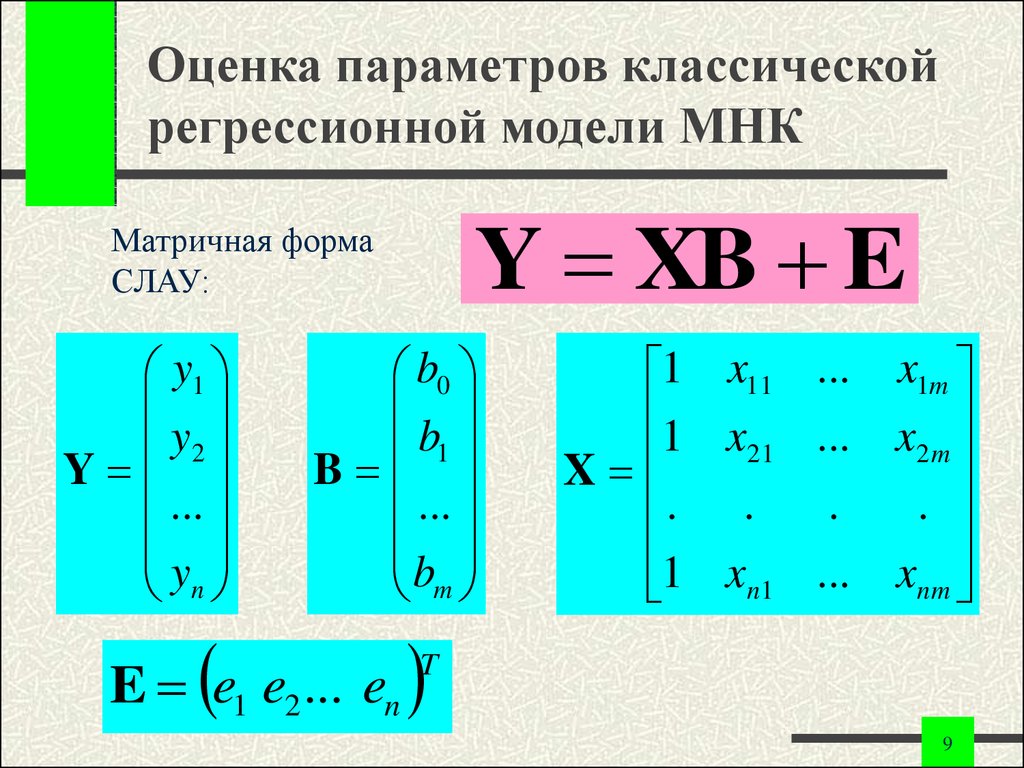
9. Оценка параметров классической регрессионной модели МНК
Y XB EМатричная форма
СЛАУ:
y1
y2
Y
...
yn
b0
b1
B
...
bm
1 x11 ... x1m
1 x
... x2 m
21
X
.
.
. .
1 xn1 ... xnm
E e1 e2 ... en
T
9
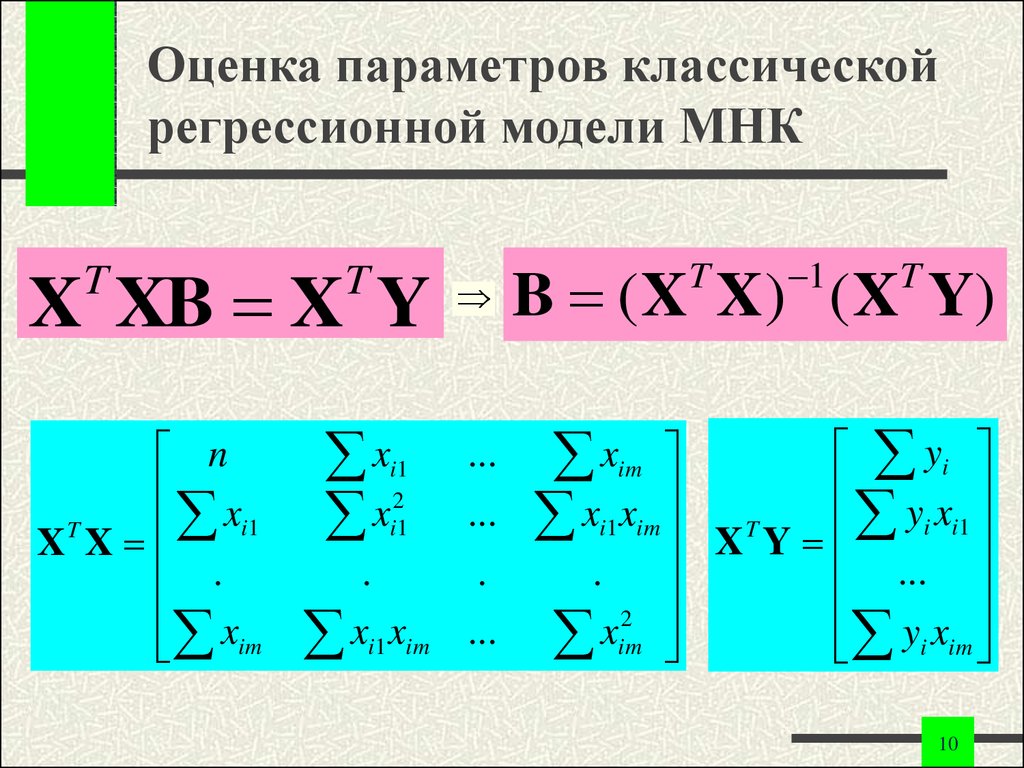
10. Оценка параметров классической регрессионной модели МНК
X XB X YT
n
xi1
T
X X
.
xim
T
x
x
i1
2
i1
.
x
...
...
.
x
i1 im
...
1
B ( X X ) ( X Y)
T
T
yi
yi xi1
i1 im
T
X Y
...
.
2
yi xim
xim
x
x x
im
10
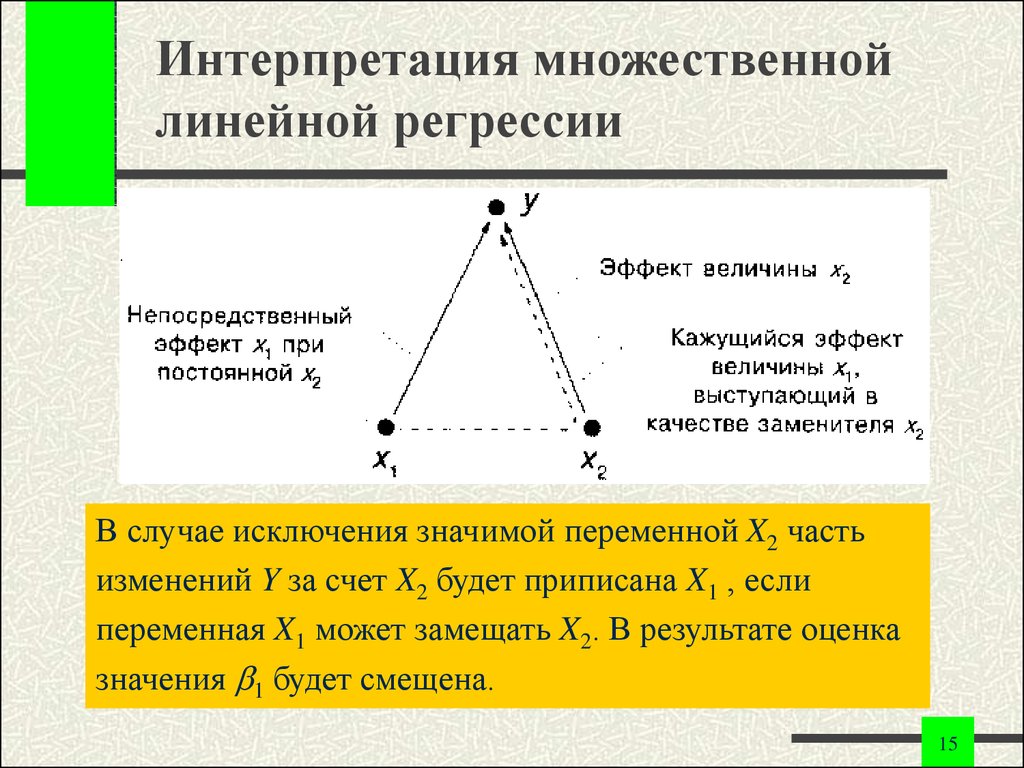
11. Интерпретация множественной линейной регрессии
Yi 0 1 X 1i 2 X 2i iИнтерпретация: коэффициент регрессии при
переменной X1 выражает предельный прирост
зависимой переменной при изменении
переменной X1 , при условии постоянства других
переменных:
dY
Y
1
,
dX 1
X 1
X 2 const
11
12. Интерпретация множественной логарифмической регрессии
ln Yi 0 1 ln X 1i 2 ln X 2i iИнтерпретация: коэффициент регрессии при
переменной lnX1 выражает эластичность
зависимой переменной при изменении
переменной X1 , при условии постоянства
других переменных:
dY X 1
Y X 1
1
,
dX 1 Y
X 1 Y
X 2 const
12
13. Интерпретация множественной линейной регрессии
Yi 0 1 X 1i 2 X 2i iОценка коэффициента регрессии:
Cov( x1 , y )Var( x2 ) Cov( x2 , y )Cov( x1 , x2 )
b1
2
Var( x1 )Var( x2 ) Cov( x1 , x2 )
Величина оценки коэффициента регрессии формируется
под влиянием не только связи изучаемого фактора с
зависимой переменной, но и структуры связей между
объясняемыми переменными
13
14. Интерпретация множественной линейной регрессии
Рассмотрим проявление множественных связей впарной регрессии (в случае исключения значимой
переменной X2):
Yi 0 1 X 1i 2 X 2i i
Yi 0 1 X 1i i
14
15. Интерпретация множественной линейной регрессии
В случае исключения значимой переменной X2 частьизменений Y за счет X2 будет приписана X1 , если
переменная X1 может замещать X2. В результате оценка
значения 1 будет смещена.
15
16. Интерпретация множественной регрессии: замещающие переменные
Замещающая переменная – это переменная,коррелирующая с отсутствующей переменной
уравнения множественной регрессии, и
выполняющая за счет этого функции
отсутствующей переменной
Включение замещающей переменной позволяет
правильно оценить роль других факторов,
освободив их от функции замещения
отсутствующих переменных
16
17. Анализ предельного вклада факторов
Множественная регрессия позволяетразложить суммарное влияние факторов на
составные части, точнее выявив
предельный вклад каждого фактора
17
18. Система показателей качества множественной регрессии
1. Показатели качества коэффициентоврегрессии
2. Показатели качества уравнения в целом
18
19. Показатели качества коэффициентов регрессии
1. Стандартные ошибки оценок.2. Значения t-статистик.
3. Интервальные оценки коэффициентов
линейного уравнения регрессии.
4. Доверительные области для зависимой
переменной.
19
20. Ковариационная матрица вектора оценок коэффициентов регрессии
00 01 ... 0 m...
10
11
1m
T
M ( B)( B)
.
.
.
.
m 0 m10 ... mm
ij Cov(bibj ) M [bi ] i M (bi i )(bj j )
На главной диагонали матрицы находятся дисперсии
оценок коэффициентов регрессии:
jj b2
j
20
21. Ковариационная матрица вектора возмущений
M [ 12 ] M [ 1 2 ]2
M
[
]
M
[
T
2 1
2]
M [ ]
M [ n 1 ] M [ n 2 ]
M [ 1 n ]
... M [ 2 n ]
2
... M [ n ]
...
Матрица обладает следующими свойствами:
1. Все элементы, не лежащие на главной диагонали, равны нулю (30).
2. Все элементы, лежащие на главной диагонали равны (10 и 20):
M [ ] M [ i 0] D[ i ]
2
i
2
2
2
2 E n
21
22. Стандартные ошибки коэффициентов
( X X )2
Можно показать, что
T
1 (1)
Поскольку истинное значение дисперсии 2 по выборке
определить нельзя, заменяем его несмещенной оценкой:
n
T
e
2
i
E E
S S
i 1
n m 1 n m 1
2
e
2
( 2)
22
23. Стандартные ошибки коэффициентов
Из (1) и (2) следует формула для расчета выборочныхдисперсий эмпирических коэффициентов регрессии:
S S z jj , j 0, m
2
bj
2
Здесь z jj , j 0, m диагональные элементы матрицы
1
Z (X X)
T
1
23
24. Стандартные ошибки коэффициентов
Как и в случае парной регрессии:Sb j S , j 0, m
2
bj
S S
2
стандартные ошибки
коэффициентов
стандартная ошибка регрессии
24
25. Стандартные ошибки коэффициентов модели с двумя переменными
Yi 0 1 X 1i 2 X 2i iРасчет стандартных ошибок коэффициентов регрессии
для случая двух факторов:
2
e
S
1
Sb j
,
j
1
,
2
2
nVar( X 1 ) 1 rx1x2
25
26. Значимость коэффициентов регрессии
Значимость коэффициентов множественной регрессиипроверяется по t-критерию Стьюдента:
t
bj
sb j
t
2
; n m 1
t
bj
sb j
расчетное значение tстатистики коэффициента bj
t-тесты обеспечивают проверку значимости предельного
вклада каждой переменной при допущении, что все
остальные переменные уже включены в модель
Незначимость коэффициента регрессии не всегда может
служить основанием для исключения соответствующей
переменной из модели
26
27. Доверительные интервалы для коэффициентов регрессии
b j t2
; n m 1
Sb j j b j t
2
; n m 1
Sb j
Данный доверительный интервал накрывает с надежностью
(1 ) истинное значение коэффициента регрессии
27
28. Доверительная область для условного математического ожидания зависимой переменной
Y p t S y ( X p ) M (Y p / X ) Y p t S y ( X p )2
T
p
;k
2
;k
m
k n m 1, Y p y ( X p ) b0 b j x pj
j 1
1
S y ( X p ) S X (X X) X p
T
p
T
28
29. Доверительная область для индивидуальных значений Y
Y p t S2
;k
y(X p )
p
Y Y p t S
2
;k
y(X p )
m
k n m 1, Y p y ( X p ) b0 b j x pj
j 1
S
y(X p )
1
S 1 X (X X) X p
T
p
T
29
30. Показатели качества уравнения регрессии в целом
1.2.
3.
4.
5.
6.
Основные показатели качества:
Коэффициент детерминации R2
2
Скорректированный коэффициент детерминации R
Значение F-статистики
Сумма квадратов остатков (RSS)
Стандартная ошибка регрессии Se
Прочие показатели: средняя ошибка аппроксимации,
индекс множественной корреляции и т.д.
30
31. Коэффициент детерминации R2
Коэффициент R2 показывает долюобъясненной вариации зависимой
переменной:
R2 1
2
e
i
2
(
y
y
)
i
R2 всегда увеличивается с включением новой переменной
Низкое значение R2 не свидетельствует о плохом
качестве модели, и может объясняться наличием
существенных факторов, не включенных в модель
Коэффициенты R2 в разных моделях с разным
числом наблюдений (и переменных) несравнимы
31
32. Скорректированный коэффициент детерминации
Скорректированныйкоэффициент
2
детерминации R
2
R показывает долю объясненной вариации зависимой
переменной с учетом числа объясняющих переменных
2
уравнения регрессии:
m
2
2
R R
n m 1
(1 R )
2
Добавление переменной приведет к увеличению R , если ее t-статистика
2
будет по модулю больше 1. Следовательно, увеличение R при добавлении
новой переменной необязательно означает, что ее коэффициент значимо
отличается от нуля
2
Скорректированные коэффициенты R в разных
моделях с разным числом наблюдений (и переменных)
ограниченно сравнимы
32
33. F-статистика для проверки качества уравнения регрессии
F-статистика представляет собой отношение объясненнойсуммы квадратов (в расчете на одну независимую переменную)
к остаточной сумме квадратов (в расчете на одну степень
свободы)
ESS
m
F
RSS
n m 1
n – число выборочных наблюдений, m – число объясняющих
переменных
33
34. F-статистика для проверки значимости коэффициента R2
F-статистика рассчитывается на основекоэффициента детерминации
ESS / m
( ESS / TSS ) / m
R2 / m
F
RSS /( n m 1) ( RSS / TSS ) /( n m 1) (1 R2 ) /( n m 1)
Для проверки значимости F-статистики используются
таблицы F-распределения с m и (n–m–1) степеней свободы
34
35. Сумма квадратов остатков RSS
Является оценкой необъясненной части вариациизависимой переменной
n
RSS e
i 1
2
i
Используется как основная минимизируемая величина в
МНК, а также для расчета других показателей
Значения RSS в разных моделях с разным числом
наблюдений и (или) переменных несравнимы
35
36. Стандартная ошибка регрессии Se
Является оценкой величины квадрата ошибки,приходящейся на одну степень свободы модели
n
Se
2
e
i
i 1
n m 1
Используется как основная величина для измерения
качества модели (чем она меньше, тем лучше)
Значения Se в однотипных моделях с разным числом
наблюдений и (или) переменных сравнимы
36
37. Расчет эластичности для линейной регрессии
Средние коэффициенты эластичности:LYX j b j
Xj
Y
Частные коэффициенты эластичности:
LYX b j
j
Xj
Y X j / X 1 , X 2 , X j 1 , X j 1 , , X M
37
38. Индекс множественной корреляции
Тесноту совместного влияния факторов нарезультат характеризует индекс (показатель)
множественной корреляции:
R R yx1 xm
2
e
2
y
S
2
1
R
S
Диапазон значений лежит от 0 до 1. Чем ближе его
значение к 1, тем теснее связь результативного признака
Y со всем набором объясняющих факторов Xi
38
39. Индекс множественной корреляции
Справедливо неравенство:Ryx1x2 xm max ryxi
i
При правильном включении факторов в модель индекс
множественной корреляции будет существенно
превосходить наибольшее из значений коэффициента
парной корреляции
39
40. Новые возможности множественной регрессии
1. Многочлены от объясняющихпеременных
2. Исследование структуры связи во
времени: запаздывающие переменные –
лаги
3. Анализ структурных сдвигов
40
41. Многочлены от объясняющих переменных
Yi 0 1 X i 2 X i iПоявляются возможности:
- исследования зависимостей, для которых
существенно наличие максимумов и минимумов,
- прямой анализ нелинейных эффектов
41
42. Лаговые переменные
Yi 0 1 X i 2 X i 1 iУчет структуры взаимосвязей во времени
зависимой и объясняющих переменных
42
43. Анализ структурных сдвигов
Тест Чоу на наличие структурного сдвигаФиктивные переменные сдвига и наклона
43
44.
Конец лекции44









































 Математика
Математика








