Похожие презентации:
Многомерный регрессионный анализ
1. Многомерный регрессионный анализ
2. Постановка задачи регрессионного анализа
Слайд №1Постановка задачи регрессионного анализа
Ставится задача на основе выборочных данных, представленных в виде
y1
y
вектора Y 2 , где yi – наблюдаемое значение результативного признака
...
yn
x11 x12 x1k
x22 x 2 k
x
Y для i-го объекта и матрицы X 21
, где xij –
x n1 x n 2 xnk
наблюдаемое значение j-го объясняющего признака для i-го объекта
выборочной совокупности, выявить «зависимость» результативного
показателя Y от факторных (объясняющих) признаков X 1 , X 2 ,..., X k .
Функция f Y ( X 1 , X 2 ,..., X k ) , описывающая зависимость условного
среднего значения результативного признака Y от заданных значений
факторных признаков X 1 , X 2 ,..., X k , называется функцией (уравнением)
регрессии, т.е. f Y ( X 1 , X 2 ,..., X k ) МY / X 1 , X 2 ,..., X k .
3. Постановка задачи регрессионного анализа
Слайд №1Постановка задачи регрессионного анализа
Ставится задача на основе выборочных данных, представленных в виде
y1
y
вектора Y 2 , где yi – наблюдаемое значение результативного признака
...
yn
x11 x12 x1k
x22 x 2 k
x
Y для i-го объекта и матрицы X 21
, где xij –
x n1 x n 2 xnk
наблюдаемое значение j-го объясняющего признака для i-го объекта
выборочной совокупности, выявить «зависимость» результативного
показателя Y от факторных (объясняющих) признаков X 1 , X 2 ,..., X k .
Функция f Y ( X 1 , X 2 ,..., X k ) , описывающая зависимость условного
среднего значения результативного признака Y от заданных значений
факторных признаков X 1 , X 2 ,..., X k , называется функцией (уравнением)
регрессии, т.е. f Y ( X 1 , X 2 ,..., X k ) МY / X 1 , X 2 ,..., X k .
4. Уравнение линейной множественной регрессии
Слайд №2Уравнение линейной множественной регрессии
5. Линейная модель множественной регрессии
Слайд №2Линейная модель множественной регрессии
6. Линейная модель множественной регрессии
Слайд №2Линейная модель множественной регрессии
~
f Y ( X 1 , X 2 ,..., X k ) Y 0 1 X 1 ... k X k ,
где 0 , 1 ,..., k – коэффициенты линейного уравнения регрессии.
Система линейных уравнений yi 0 1 xi1 2 xi2 ... k xik i ,
где i – регрессионный остаток, характеризующий расхождение
между наблюдаемым значением y i и «осредненным» значением ~
yi ,
i 1, n ;
или
Y X , ( 0 ,..., k ) , ( 1 ,..., n ) T ,
1 x11 x12 x1k
1 x21 x22 x2k
X
1 xn1 x n 2 xnk
называется линейной моделью множественной регрессии.
7. Геометрическая интерпретация функции регрессии
Слайд №3Геометрическая интерпретация функции регрессии
y
~
y 0 1x1
yi
ei
~
yi
xi1
x
8. Классическая линейная модель множественной регрессии (КЛММР)
Слайд №4Линейная
модель
множественной
регрессии,
удовлетворяющая следующим пяти требованиям, называется
классической линейной моделью множественной регрессии.
Условия Гаусса–Маркова
1) X 1 , X 2 ,..., X k – детерминированные переменные;
2) ранг матрицы Х равен k+1 – среди признаков нет линейно
зависимых;
3) M i 0 , i 1, n – нет систематических ошибок в измерении Y;
4) D i M i2 2 , i 1, n – гомоскедастичность регрессионных
остатков (равноточные измерения);
5) cov( i , j ) M ( i j ) 0 – условие некоррелированности
регрессионных остатков, i j , i 1, n , j 1, n .
9. Классическая линейная модель множественной регрессии (КЛММР)
10. Методы оценки коэффициентов КЛММР
Слайд №5Методы оценки коэффициентов КЛММР
Оценку коэффициентов уравнения регрессии можно
искать:
исходя из требований минимума модуля отклонения
наблюдаемых значений yi от "значений" функции
регрессии
исходя из критерия минимума суммы квадратов
отклонений наблюдаемых значений yi от "значений"
функции регрессии (метод наименьших квадратов)
11. Методы оценки коэффициентов КЛММР
Слайд №5Методы оценки коэффициентов КЛММР
12. Метод наименьших квадратов
Слайд №6Метод наименьших квадратов
n
F ( yi b0 b1xi1 b2 xi 2 ... bk xin )
i 1
2
13. Метод наименьших квадратов
Слайд №6Метод наименьших квадратов
n
F ( yi b0 b1xi1 b2 xi 2 ... bk xin )
2
i 1
T
(Y Xb) (Y Xb)
14. Метод наименьших квадратов
Слайд №6Метод наименьших квадратов
n
F ( yi b0 b1 xi1 b2 xi 2 ... bk xin )
2
i 1
T
(Y Xb) (Y Xb)
T
T
T
T
T
T
Y Y b X Y Y Xb b X Xb
T
T
T
T
T
Y Y 2b X Y b X Xb min .
15. Метод наименьших квадратов
Слайд №6Метод наименьших квадратов
n
F ( yi b0 b1 xi1 b2 xi 2 ... bk xin )
2
i 1
T
(Y Xb) (Y Xb)
T
T
T
T
T
T
Y Y b X Y Y Xb b X Xb
T
T
T
T
T
Y Y 2b X Y b X Xb min .
2 X Xb 2 X Y 0
T
T
16. Метод наименьших квадратов
Слайд №6Метод наименьших квадратов
n
F ( yi b0 b1 xi1 b2 xi 2 ... bk xin )
2
i 1
T
(Y Xb) (Y Xb)
T
T
T
T
T
T
Y Y b X Y Y Xb b X Xb
T
T
T
T
T
Y Y 2b X Y b X Xb min .
2 X Xb 2 X Y 0
T
T
1
bМНК b ( X X ) X Y
T
T
17. Метод наименьших квадратов
Слайд №6Метод наименьших квадратов
n
F ( y i b0 b1 x i1 b2 x i 2 ... bk x in ) 2 (Y X b ) T (Y X b )
i 1
Y T Y b T X T Y Y T X b b T X T X b Y T Y 2b T X T Y b T X T X b min
2 X T Xb 2 X T Y 0
В силу предположения о справедливости условий ГауссаМаркова, в частности (Х=k+1), матрица ХТХ – не вырождена и
получим МНК - оценки для вектора :
bМНК b ( X T X ) 1 X T Y
оценка уравнения регрессии:
yˆ b0 b1 x1 b2 x 2 ... bk x k
( Sb 0 )
( sb1 )
( Sb 2 )
( Sbk )
18.
Теорема Гаусса — МарковаЕсли выполнены условия (1)–(5),
то оценка коэффициентов модели,
полученная по методу наименьших
квадратов, является:
(а) несмещенной
(б) эффективной
19. Статистические свойства оценок коэффициентов, полученных МНК
Слайд №7Статистические свойства оценок коэффициентов,
полученных МНК
20. Статистические свойства оценок коэффициентов, полученных МНК
Слайд №7Статистические свойства оценок коэффициентов,
полученных МНК
21. Статистические свойства оценок коэффициентов, полученных МНК
Слайд №7Статистические свойства оценок коэффициентов,
полученных МНК
22. Статистические свойства оценок коэффициентов, полученных МНК
Слайд №7Статистические свойства оценок коэффициентов,
полученных МНК
23. Статистические свойства оценок коэффициентов, полученных МНК
Слайд №7Статистические свойства оценок коэффициентов,
полученных МНК
24. Статистические свойства оценок коэффициентов, полученных МНК
Слайд №7Статистические свойства оценок коэффициентов,
полученных МНК
bМНК b ( X T X ) 1 X T Y
b ( X T X ) 1 X T Y ( X T X ) 1 X T ( X ) ( X T X ) 1 X T .
1) МНК – оценка b является несмещенной оценкой вектора
b ( X T X ) 1 X T Y ( X T X ) 1 X T ( X ) ( X T X ) 1 X T
Mb M ( ( X T X ) 1 X T ) ( X T X ) 1 X T M
2) Свойство состоятельности в данном случае определяется
структурой матрицы Х: наименьшее собственное число матрицы
X T X стремится к , при n .
3) Оценки
считаются
эффективными,
если
они
характеризуются наименьшей дисперсией. Эффективность МНКоценок доказывается в предположении о нормальности
регрессионных остатков ММП.
25.
26.
27. Ковариационная матрица вектора оценок коэффициентов
Найдем ковариационную матрицу случайного вектора b, воспользовавшисьусловиями Гаусса-Маркова
b M [(b Mb)(b Mb)T ]
Слайд №8
28. Ковариационная матрица вектора оценок коэффициентов
Слайд №8Найдем ковариационную матрицу случайного вектора b, воспользовавшись
условиями Гаусса-Маркова
b M [(b Mb)(b Mb)T ] M [(( X T X ) 1 X T )(( X T X ) 1 X T )T )]
29. Ковариационная матрица вектора оценок коэффициентов
Слайд №8Найдем ковариационную матрицу случайного вектора b, воспользовавшись
условиями Гаусса-Маркова
b M [(b Mb)(b Mb)T ] M [(( X T X ) 1 X T )(( X T X ) 1 X T )T )]
M [( X T X ) 1 X T T ( X T X ) 1 ]
30. Ковариационная матрица вектора оценок коэффициентов
Слайд №8Найдем ковариационную матрицу случайного вектора b, воспользовавшись
условиями Гаусса-Маркова
b M [(b Mb)(b Mb)T ] M [(( X T X ) 1 X T )(( X T X ) 1 X T )T )]
M [( X T X ) 1 X T T ( X T X ) 1 ] ( X T X ) 1 X T M ( T ) X ( X T X ) 1
31. Ковариационная матрица вектора оценок коэффициентов
Слайд №8Найдем ковариационную матрицу случайного вектора b, воспользовавшись
условиями Гаусса-Маркова
b M [(b Mb)(b Mb)T ] M [(( X T X ) 1 X T )(( X T X ) 1 X T )T )]
T
1 T T
T
1
T
1 T
T
T
1
M [( X X ) X ( X X ) ] ( X X ) X M ( ) X ( X X )
( X T X ) 1 X T 2 n X ( X T X ) 1
32. Ковариационная матрица вектора оценок коэффициентов
Слайд №8Найдем ковариационную матрицу случайного вектора b, воспользовавшись
условиями Гаусса-Маркова
b M [(b Mb)(b Mb) T ] M [(( X T X ) 1 X T )(( X T X ) 1 X T ) T )]
M [( X T X ) 1 X T T ( X T X ) 1 ] ( X T X ) 1 X T M ( T ) X ( X T X ) 1
( X T X ) 1 X T 2 n X ( X T X ) 1 2 ( X T X ) 1 .
33. Ковариационная матрица вектора оценок коэффициентов
.Слайд №8
Найдем ковариационную матрицу случайного вектора b, воспользовавшись
условиями Гаусса-Маркова
b M [(b Mb)(b Mb) T ] M [(( X T X ) 1 X T )(( X T X ) 1 X T ) T )]
M [( X T X ) 1 X T T ( X T X ) 1 ] ( X T X ) 1 X T M ( T ) X ( X T X ) 1
( X T X ) 1 X T 2 n X ( X T X ) 1 2 ( X T X ) 1 .
Откуда,
частности,
2
в
T
1
Dbj [( X X ) ] jj ,
_____
j 0, k
34. Ковариационная матрица вектора оценок коэффициентов
.Слайд №8
Найдем ковариационную матрицу случайного вектора b, воспользовавшись
условиями Гаусса-Маркова
b M [(b Mb)(b Mb) T ] M [(( X T X ) 1 X T )(( X T X ) 1 X T ) T )]
M [( X T X ) 1 X T T ( X T X ) 1 ] ( X T X ) 1 X T M ( T ) X ( X T X ) 1
( X T X ) 1 X T 2 n X ( X T X ) 1 2 ( X T X ) 1 .
Откуда,
частности,
2
в
T
1
Dbj [( X X ) ] jj ,
_____
j 0, k
35. Качество подгонки модели
1.Стандартная ошибка регрессии
2.
Коэффициент детерминации R2
3.
Скорректированный (нормированный)
коэффициент детерминации R2
36. Стандартная ошибка регрессии
37. Анализ вариации результативного признака Коэффициент детерминации R2
В качестве характеристики степени рассеивания случайной величиныY относительно функции регрессии используется в случае нелинейной связи
корреляционное отношение:
M (Y f Y ( X 1 , X 2 ,..., X k )) 2 M ( f Y ( X 1 , X 2 ,..., X k ) MY ) 2
2
Y / X1 ,..., X k 1
,
2
2
Y
Y
которое характеризует качество подгонки функции регрессии под
выборочные данные. В случае линейной регрессии Y2 / X1 ,..., X k называется
коэффициентом детерминации RY2 / X1 ,..., X k R 2 .
Коэффициент детерминации строится из тех соображений, что общая
дисперсия результативного признака складывается из факторной и
остаточной дисперсий:
2
2
Y2 факт
ост
,
где Y2 – дисперсия результативного признака;
2
факт
М ( f Y ( X 1 ,..., X k ) MY ) 2 – факторная дисперсия;
2
2
38.
Y2 / X1 ,..., X k1
M (Y f Y ( X 1 , X 2 ,..., X k )) 2
Y2
M ( f Y ( X 1 , X 2 ,..., X k ) MY ) 2
Y2
Слайд, №9
Анализ вариации результативного признака
которое характеризует Коэффициент
качество подгонки
функции
регрессии под
детерминации
R2
выборочные данные. В случае линейной регрессии Y2 / X1 ,..., X k называется
коэффициентом детерминации RY2 / X1 ,..., X k R 2 .
Коэффициент детерминации строится из тех соображений, что общая
дисперсия результативного признака складывается из факторной и
остаточной дисперсий:
2
2
Y2 факт
ост
,
где Y2 – дисперсия результативного признака;
2
факт
М ( f Y ( X 1 ,..., X k ) MY ) 2 – факторная дисперсия;
2
ост
М (Y f Y ( X 1 ,..., X k )) 2 – остаточная дисперсия.
39.
Анализ вариации результативного признакаКоэффициент детерминации R2
40.
Анализ вариации результативного признакаКоэффициент детерминации R2
41. Анализ вариации результативного признака Выборочный коэффициент детерминации
42. О чем говорит и о чем не говорит R2
Выборочный коэффициент детерминации находитсяв промежутке [0;1]
Характеризует долю общей вариации
результативного признака у, объясняемую вариацией
выборочной функции регрессии .
Чем меньше разброс статистических данных
относительно уравнения регрессии, тем меньше
остаточная дисперсия, и тем ближе R2 к единице.
42
43. О чем говорит и о чем не говорит R2
ВысокийR2 сам по себе не гарантирует, что модель
является хорошей.
Остается риск ложной регрессии
Низкий R2 говорит о том, что существуют важные факторы,
которые мы не учли в нашей модели
43
44.
О чем говорит и о чем не говорит R2Высокий R2 сам по себе не гарантирует, что модель
является хорошей.
Остается риск ложной регрессии
Низкий R2 говорит о том, что существуют важные
факторы, которые мы не учли в нашей модели
44
45.
Использование R2 и R2сЕсть соблазн свести выбор уравнения к задаче
максимизации R2 или R2с. Не стоит этого делать.
1.Высокий R2 (или R2с) говорит о том, что регрессоры
предсказывают большую долю изменений y.
2.Высокий R2 (или R2с) не говорит о том, что вы верно
выявили причинно-следственную связь между
переменными
3.Высокий R2 (или R2с) не гарантирует отсутствия
смещения оценок из-за некорректной спецификации
45
45
46.
Тестирование гипотез1.
2.
3.
4.
46
Тестирование значимости уравнения
Тестирование значимости коэффициента
Доверительный интервал для коэффициента
Построение доверительного интервала для среднего
значения предсказания и для конкретного
предсказанного значения
46
47.
Слайд №11Проверка гипотезы об адекватности линейной
модели выборочным данным
Исследование свойств оценок классической линейной модели
множественной регрессии проводится при дополнительном
предположении
и
нормальном
характере
распределения
регрессионных остатков:
i N (0, 2 ), i 1...n .
Н0: β1=β2=…=βk=0
(линейная модель множественной регрессии
неадекватна выборочным данным);
Н1: j [1, n] : j 0 (линейная модель множественной регрессии
адекватна выборочным данным).
Для проверки гипотезы Н0 используется статистика:
RˆY2 / X1 ,..., X k / k
Qфакт / k
,
F
2
ˆ
Qост /( n k 1) (1 RY / X ,..., X ) /( n k 1)
1
k
которая в случае справедливости Н0 имеет распределение Фишера с
числом степеней свободы 1 k и 2 n k 1.
48.
Проверка гипотезы об адекватности линейной модели выборочным данным48
48
49.
Проверка гипотезы об адекватности линейноймодели выборочным данным
49
49
50.
Проверка гипотезы об адекватности линейной модели выборочным данным50
50
51.
Проверка гипотезы об адекватности линейной модели выборочным данным51
51
52.
Слайд №12Проверка гипотезы о значимости коэффициентов
КЛММР
Н0: βj=0 (коэффициент βj незначимо отличен от нуля);
Н1: βj 0 (коэффициент βj – значимо отличен от нуля).
Для проверки таких гипотез Н0 строятся статистики
t
bj
Sb j
,
j 1,2,..., k , S b j Sˆ [( X T X ) 1 ] jj ,
которые в случае справедливости Н0, имеют распределение Стьюдента с
n k 1 степенями свободы.
Для коэффициентов уравнения регрессии значимо отличных от нуля
находим доверительные интервалы, используя статистику
bj j
t
Sb j
имеющую распределение Стьюдента с n k 1 степенями свободы.
53.
Проверка гипотезы о значимости коэффициентов КЛММР53
53
54.
Проверка гипотезы о значимости коэффициентов КЛММР54
54
55.
Проверка гипотезы о значимости коэффициентов КЛММР55
55
56.
Проверка гипотезы о значимости коэффициентов КЛММР56
56
























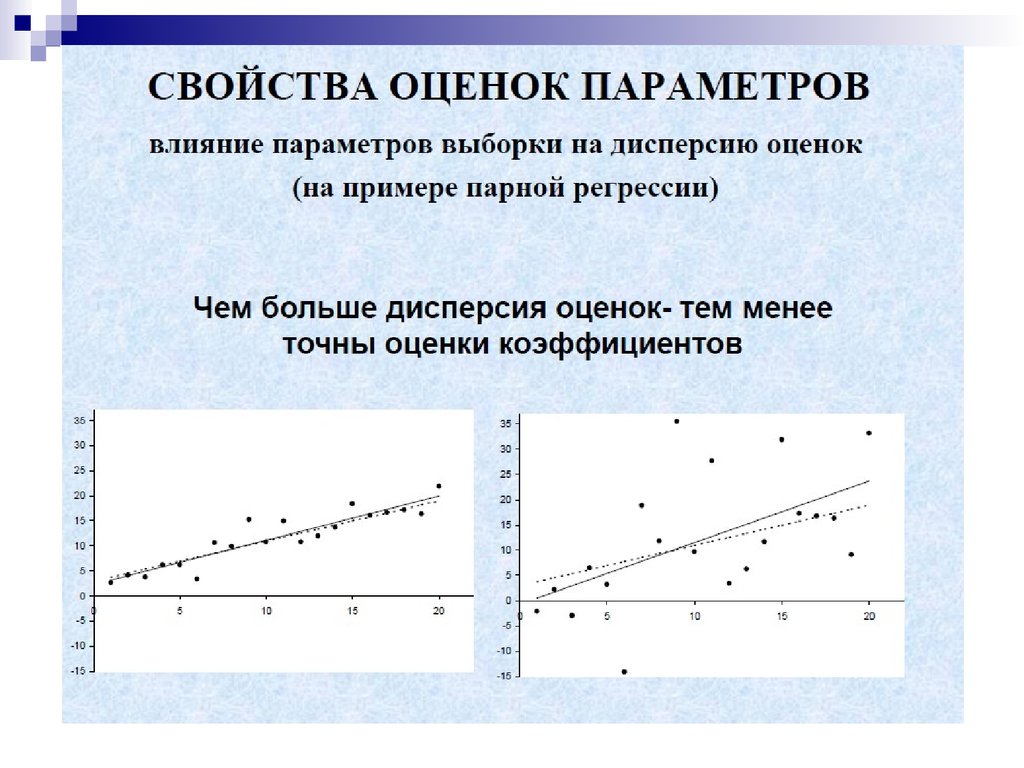
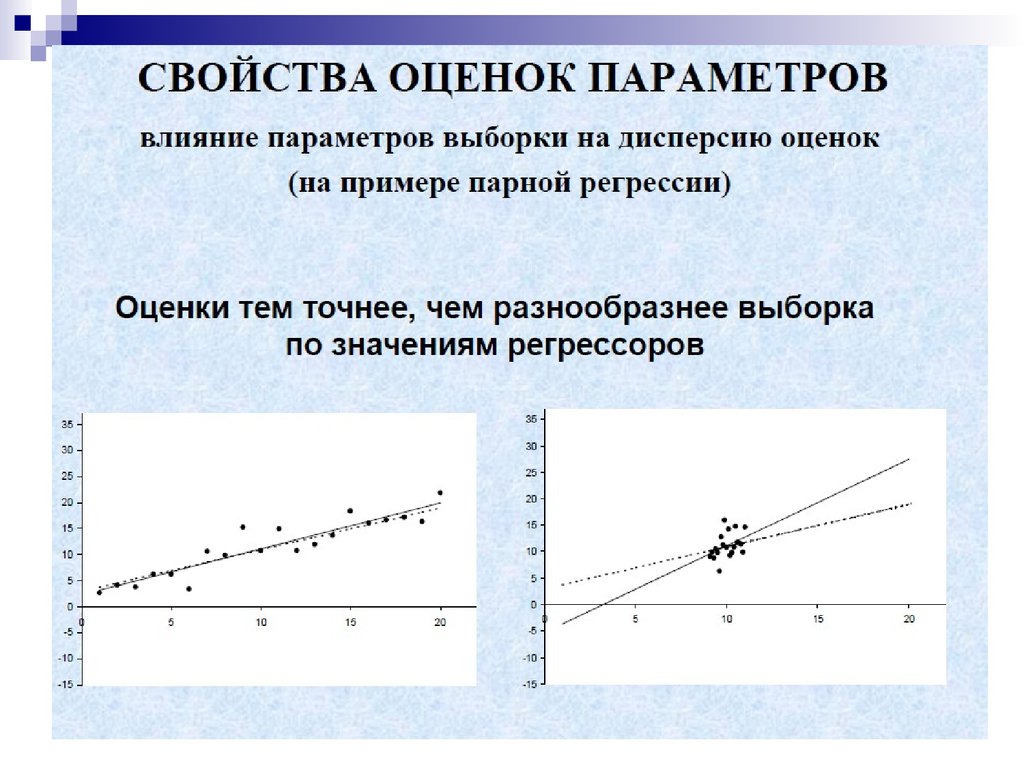

































 Математика
Математика








