Похожие презентации:
Предел функции. Лекция 5
1.
Ащеулова Алена Сергеевна,кандидат физико-математических наук
2.
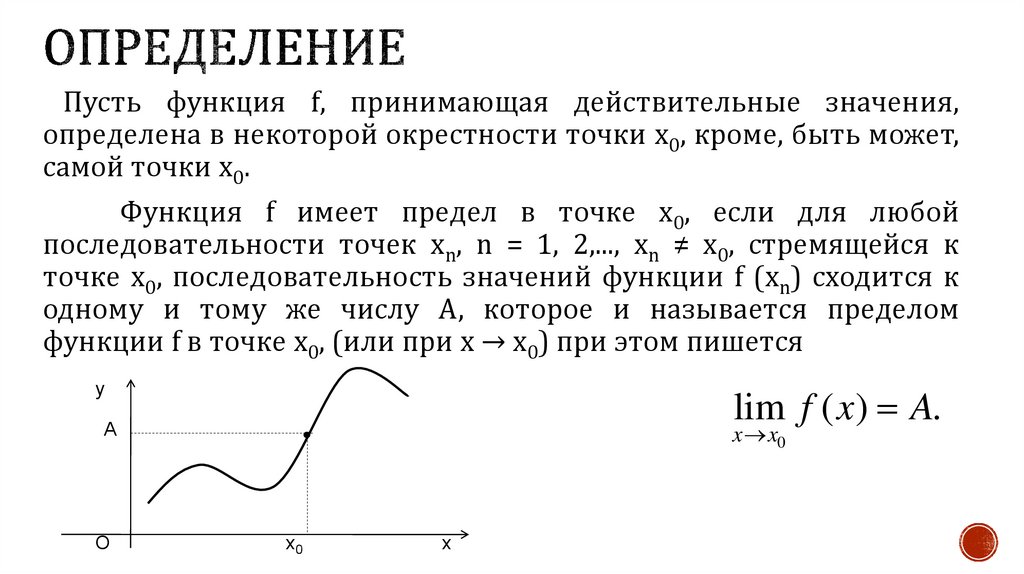
Пусть функция f, принимающая действительные значения,определена в некоторой окрестности точки x0, кроме, быть может,
самой точки x0.
Функция f имеет предел в точке x0, если для любой
последовательности точек xn, n = 1, 2,..., xn ≠ x0, стремящейся к
точке x0, последовательность значений функции f (xn) сходится к
одному и тому же числу А, которое и называется пределом
функции f в точке x0, (или при x → x0) при этом пишется
у
lim f ( x) A.
А
О
x x0
х0
х
3.
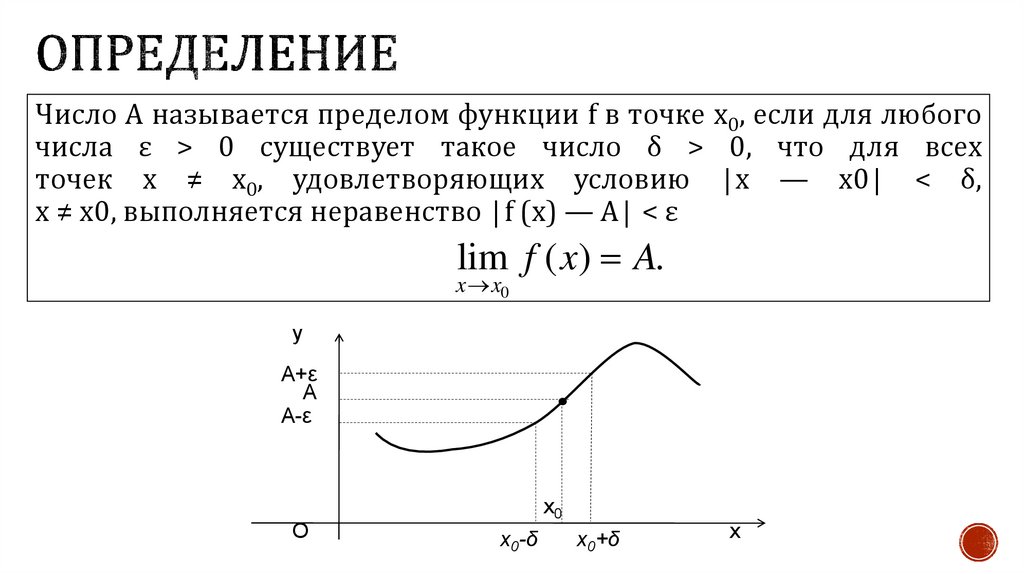
Число А называется пределом функции f в точке x0, если для любогочисла ε > 0 существует такое число δ > 0, что для всех
точек х ≠ x0, удовлетворяющих условию |х — x0| < δ,
x ≠ x0, выполняется неравенство |f (x) — A| < ε
lim f ( x) A.
x x0
у
А+ε
А
А-ε
О
х0
х0-δ
х0+δ
х
4.
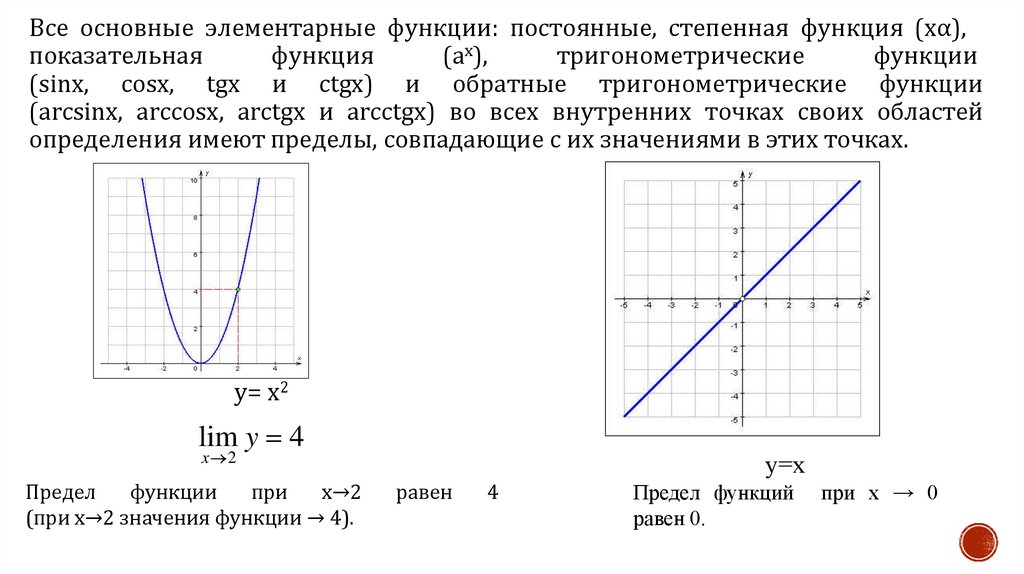
Все основные элементарные функции: постоянные, степенная функция (хα),показательная
функция
(ax),
тригонометрические
функции
(sinx, cosx, tgx и ctgx) и обратные тригонометрические функции
(arcsinx, arccosx, arctgx и arcctgx) во всех внутренних точках своих областей
определения имеют пределы, совпадающие с их значениями в этих точках.
у= x2
lim y 4
x 2
Предел
функции
при
x→2
(при x→2 значения функции → 4).
y=x
равен
4
Предел функций
равен 0.
при x → 0
5.
Если функции f (x) и g (x) имеют конечные пределы в точке a, причемlim f ( x) A
x a
То
lim g ( x) B
x a
lim f ( x) g ( x) A B
x a
lim f ( x) g ( x) A B
x a
f ( x) A
lim
x a g ( x)
B
если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.
6.
lim x 2 5 x 8x 5 x 8 x 3
3 5 3 8 9 15 8 2
lim 2
2
0, 2
2
x 3 x x 4
3 3 4
9 3 4 10
lim x x 4
2
x 3
lim sin x
x
2
lim cos 2 x
x
2
x 0,5 x
lim
2
7.
При нахождении предела иногда сталкиваются с неопределенностямивида
0
0
0
,
,
,
1
,
0
,
0
,
.
0
Отыскание предела
неопределенности.
в
таких
случаях
называется
Для того, чтобы раскрыть неопределенность
числитель и знаменатель на х в старшей степени.
необходимо разделить
2 x 2 3x 5
2
2 x 2 3 x 5 разделим
x
lim
lim
lim
2
2
x 1 x 3 x 2
x
x
1 x 3x
на x
0
0
x2
3 5
2 2
x x 2
lim
x 1
1
3
3
x2 x
0
0
раскрытием
2 x 2 3x 5
2 2
2
x
x
x
1
x 3x 2
2 2
2
x
x
x
8.
7 x 3 15 x 2 9 x 5lim
4
2
x
5x 7 x 5
3x 2 6 x 5
lim
x
x 5
x 4 6 x 2 12
lim 4
x 4 x 4 х 3
x 4 6 x 2 12
lim 4
x 4 x 4 х 3
3 x 2 12 x 9
lim
2
x 4 x х 4




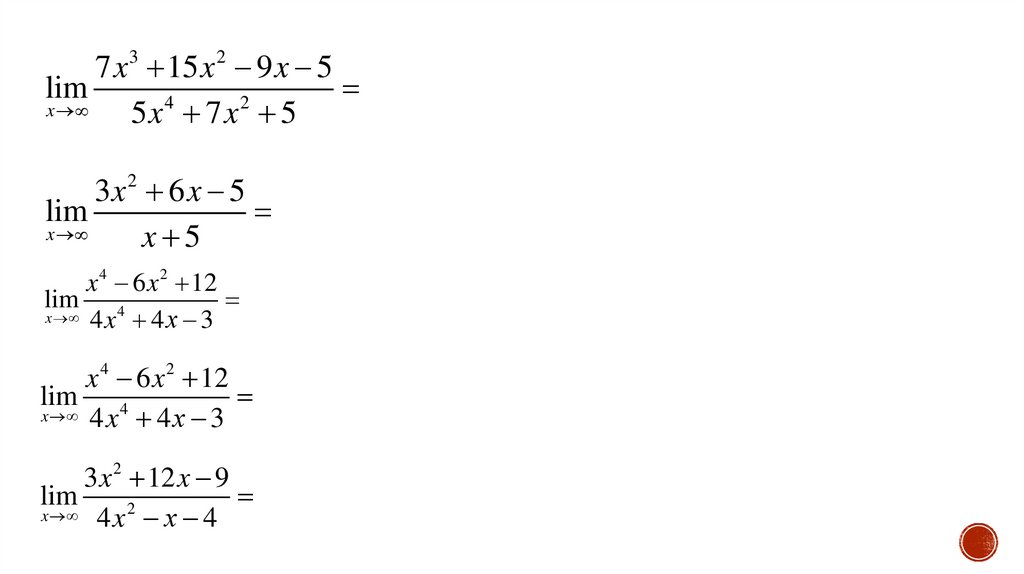
 Математика
Математика








