Векторы и действия над ними

1.

2.

Направленный отрезок, на котором
заданы начало, конец и направление,
называется вектором.
Обозначается:
a ; AB
a
A
B

3.

Длиной или модулем вектора называется
расстояние между его началом и концом.
Обозначается:
a ; AB
Векторы, лежащие на одной прямой или
на параллельных прямых, называются
коллинеарными.
Если начало и конец вектора совпадают,
то вектор называется нулевым.

4.

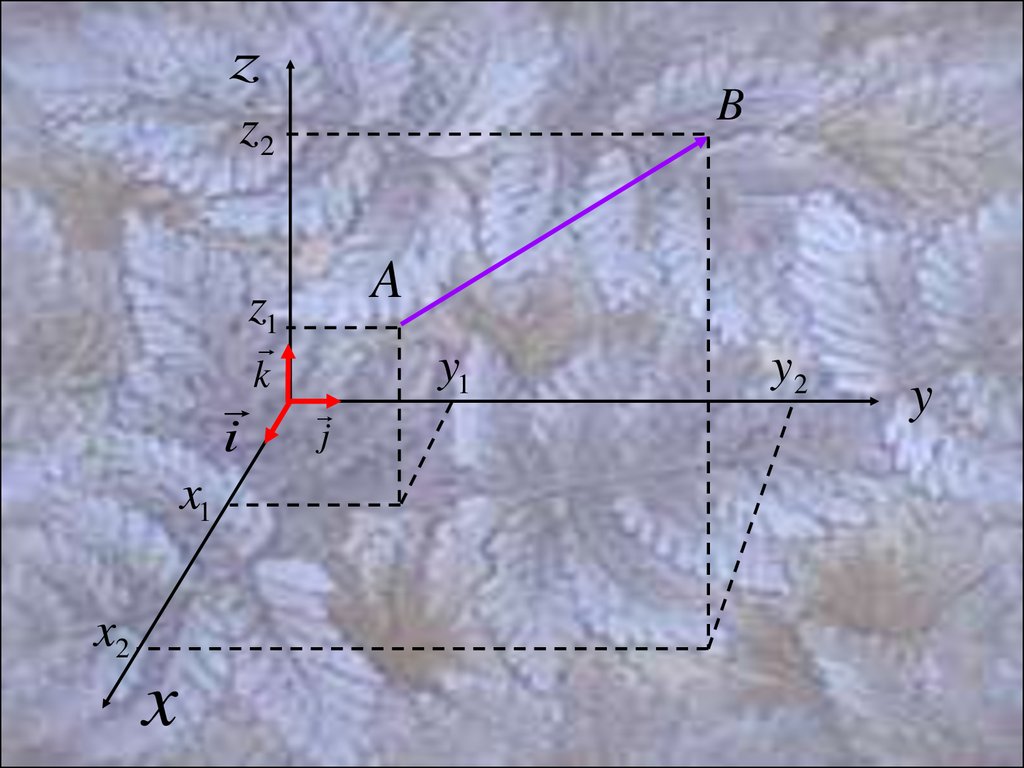
В любой системе отсчета вектор характеризуется
своими координатами.
Пусть в системе отсчета XYZ заданы координаты
начала и конца вектора:
A( x1, y1, z1 ) B( x2 , y2 , z2 )
Тогда координаты вектора будут:
AB ( x, y, z)
Где:
x x2 x1 Или:
y y2 y1
z z2 z1
AB x i y j z k

5.

z
B
z2
A
z1
i
x1
x2
x
k
j
y1
y2
y

6.

Длина вектора определяется по формуле:
AB ( x2 x1 ) ( y2 y1 ) ( z2 z1 )
2
2
x y z
2
2
2
2

7.

Пусть два вектора заданы своими координатами:
a (a1 , a2 , a3 ) b (b1 , b2 , b3 )
Если
эти
вектора
коллинеарны,
то
их
соответствующие
координаты
должны
быть
пропорциональны:
a1 a2 a3
b1 b2 b3

8.

Суммой двух векторов будет вектор,
координаты которого равны суммам
соответствующих координат исходных
векторов.
a (a1 , a2 , a3 ) b (b1 , b2 , b3 )
c a b
c (c1 , c2 , c3 )
c1 a1 b1 c2 a2 b2
c3 a3 b3

9.

Для построения суммы векторов, нужно совместить
конец первого вектора с началом второго. Тогда
вектор их суммы будет направлен от начала первого
вектора к концу второго:
b
a
c a b
Аналогично определяется сумма нескольких векторов.

10.

Разностью двух векторов a b
называется сумма векторов a ( b )
b
a
b
c a b
a

11.

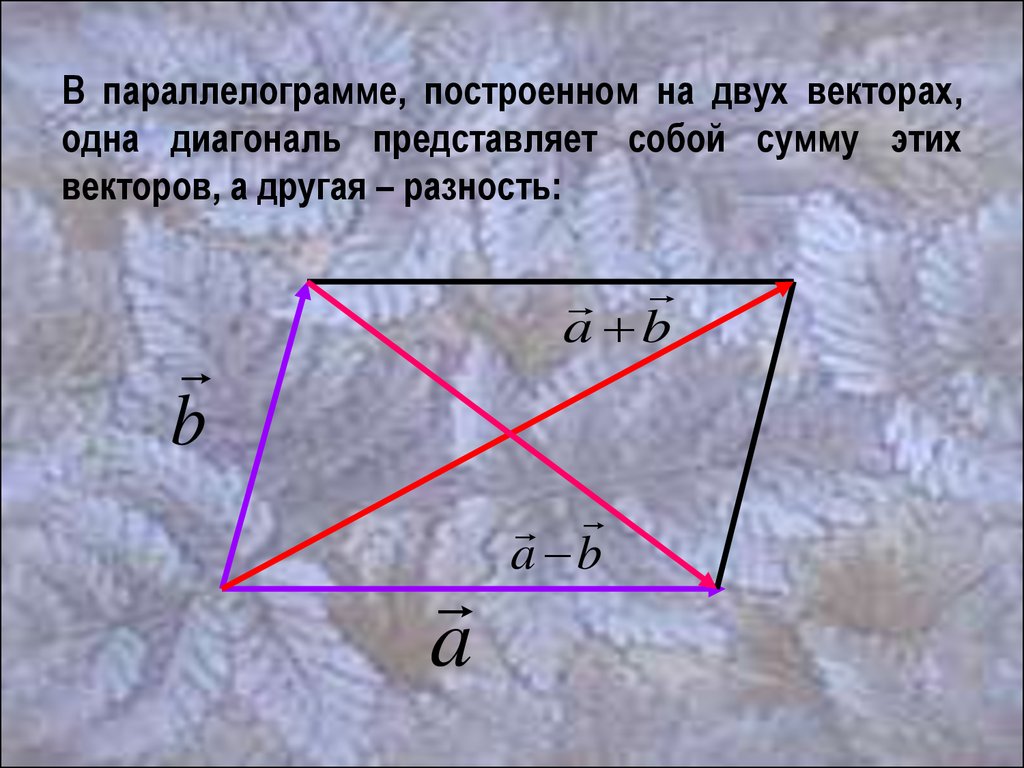
В параллелограмме, построенном на двух векторах,
одна диагональ представляет собой сумму этих
векторов, а другая – разность:
a b
b
a
a b

12.

Произведением вектора на число будет
вектор, координаты которого равны
произведению соответствующих
координат исходного вектора на это
число.
a (a1 , a2 , a3 )
a c
c1 a1
c (c1 , c2 , c3 )
c2 a2
c3 a3

13.

Геометрически смысл умножения вектора
на число заключается в увеличении его
длины в λ раз, если lλl>1, и в ее сокращении
во столько же раз при lλl<1.

14.

1
a b b a
2
(a b ) c a (b c )

15.

3
( a ) ( )a
4
( )a a a
5
(a b ) a b

16.

Скалярным произведением двух
векторов называется число, равное
произведению длин этих векторов на
косинус угла между ними.
(a, b ) a b cos a ; b

17.

Если два вектора заданы своими координатами:
a (a1 , a2 , a3 ) b (b1 , b2 , b3 )
То скалярное произведение выразится следующим
образом:
(a , b ) a1b1 a2b2 a3b3
Отсюда можно
векторами:
выразить
угол
(a , b )
cos a ; b
a b
между
двумя

18.

Если два вектора перпендикулярны, то их скалярное
произведение должно быть равно нулю:
(a, b ) a1b1 a2b2 a3b3 0