«Комплексные числа и действия над ними»

1.

«Комплексные числа и
действия
над ними»

2. Какие числовые множества Вам знакомы?

N
Z
Q
N Z Q R
R

3.

Числовая система
Натуральные
числа, N
Целые числа, Z
Рациональные числа, Q
Действительные числа,
R
Комплексные
числа, C
Допустимые
алгебраические
операции
Сложение,
умножение
Сложение, вычитание,
умножение
Сложение, вычитание,
умножение, деление
Сложение, вычитание,
умножение, деление,
извлечение корней из
неотрицательных чисел
Все операции
Частично
допустимые
алгебраические
операции
Вычитание, деление,
извлечение корней
Деление,
извлечение корней
Извлечение корней из
неотрицательных
чисел
Извлечение корней
из произвольных
чисел

4. «Мнимые числа»

«МНИМЫЕ ЧИСЛА»

5. Рассмотрим понятие мнимого числа при решении неполного квадратного уравнения.

6.

Рассмотрим неполное квадратное
уравнение:
x2 = a ,
где а – известная величина. Решение
этого
уравнения можно записать как:

7. Здесь возможны три случая:

1 случай:
Если a = 0 , то
x = 0.

8. 2 случай:

• Если а – положительное
число, то его квадратный
корень имеет два
значения: одно
положительное, другое
отрицательное; например,
уравнение x 2 = 25 имеет
два корня: 5 и – 5. Это
часто записывается как
корень с двойным знаком:

9. 3 случай:

• Если а – отрицательное
число, то это уравнение
не имеет решений среди
известных нам
положительных и
отрицательных чисел,
потому что вторая
степень любого числа
есть число
неотрицательное.

10.

Но если мы хотим получить
решения уравнения x 2 = a также и
для отрицательных значений а , мы
вынуждены ввести числа нового
типа – мнимые числа.

11. Таким образом

• мнимым называется
число, вторая степень
которого является
числом
отрицательным.
Согласно этому
определению мнимых чисел
мы можем определить и
мнимую единицу:

12.

Тогда для уравнения x 2 = – 25 мы
получаем два мнимых корня:

13. Мнимые числа

i = -1, i – мнимая единица
i, 2i, -0,3i — чисто мнимые числа
Арифметические операции над чисто мнимыми числами
выполняются в соответствии с условием .
3i 13i 3 13 i 16i
3i 13i 3 13 i i 39i 2 39
i 7 i 2 i i
3
В общем виде правила арифметических операций с чисто
мнимыми числами таковы:
a b i;
a bi ab i;
ai bi
ai bi a b i;
ai bi abi a
где a и b — действительные числа.
2

14. Комплексные числа

Определение 1. Комплексным числом называют сумму
действительного числа и чисто мнимого числа.
z a bi C a R, b R,
i мнимая единица.
a Re z , b Im z
Определение 2. Два комплексных числа называют
равными, если равны их действительные части и равны
их мнимые части:
a bi c di a c, b d .

15.

Сумма действительного и мнимого числа
называется комплексным числом
и обозначается:
a+bi,
где a, b – действительные числа, i – мнимая
единица.

16. Классификация комплексных чисел

Комплексные числа
a + bi
Действительные числа
b=o
Рациональные
числа
Иррациональные
числа
Мнимые числа
b≠o
Мнимые числа с
ненулевой
действительной
частью
a ≠ 0, b ≠ 0.
Чисто
мнимые
числа
a = 0, b ≠ 0.

17.

Впервые мнимые величины
появились в известном труде
«Великое искусство, или об
алгебраических правилах» Кардано
(1545), который счёл их
непригодными к употреблению.

18.

Пользу мнимых величин, в частности, при
решении
кубического уравнения, в так называемом
неприводимом случае впервые
оценил Бомбелли (1572). Он же дал
некоторые простейшие правила действий с
комплексными числами.

19.

Выражения вида
,
появляющиеся при решении
квадратных и
кубических уравнений, стали
называть «мнимыми» в XVI—XVII веках,
однако даже для многих крупных
ученых XVII века алгебраическая
и геометрическая сущность мнимых
величин представлялась неясной.

20.

Символ предложил Эйлер (1777), взявший для
этого первую букву слова лат. imaginarius. Он же
распространил все стандартные функции,
включая логарифм, на комплексную область. К
такому же выводу пришел д’Аламбер (1747), но
первое строгое доказательство этого факта
принадлежит Гауссу (1799). Гаусс и ввёл в
широкое употребление термин «комплексное
число» в 1831 году, хотя этот термин ранее
использовал в том же смысле французский
математик Лазар Карно в 1803 году.

21.

Основные понятия
Комплексным числом z называется выражение вида z=a+ib, где a и
b – действительные числа, i – мнимая единица, которая определяется
соотношением:
i 2 1;
i 1.
При этом число a называется действительной частью числа z
, а b - мнимой частью.
Числа z=a+ib и
z a ib называются комплексно – сопряженными.
Два комплексных числа z1=a1+ib1 и z2=a2+ib2 называются равными, если
соответственно равны их действительные и мнимые части:
a1=a2;
b1=b2
Комплексное число равно нулю, если соответственно равны нулю
действительная и мнимая части
a=b=0.
Также комплексные числа можно записывать, например, в виде z=x+iy,
z=u+iv.
содержание

22. Изображение комплексных чисел на координатной плоскости.

23. Каждое комплексное число z=a+bi геометрически изображается на плоскости как точка M(a;b) или как вектор ОМ с началом в точке

O(0;0) и концом в
точке M(a;b).

24.

25. Пример. Изобразить на плоскости комплексные числа:

z1 2 4i; z 2 5;
z 3 4 i; z 4 3i;
z 5 5 2i; z 6 3 5i .

26.

z1

27.

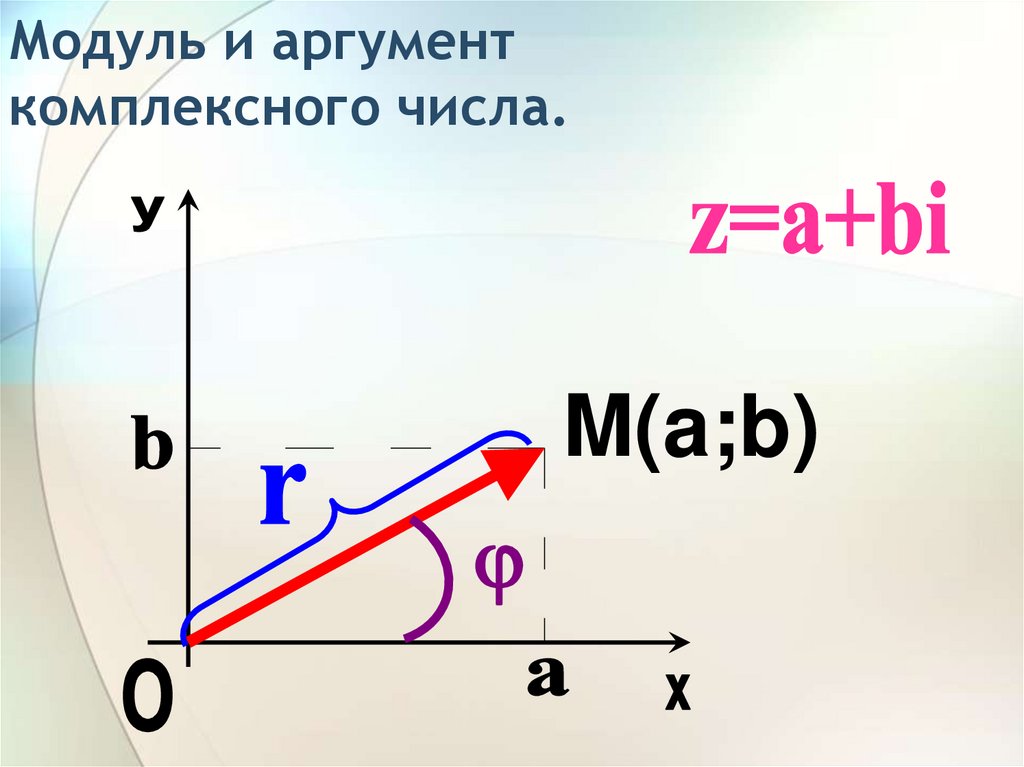
28. Модуль и аргумент комплексного числа.

M(a;b)

29. Модулем комплексного числа z=a+bi называется длина вектора, соответствующего этому числу. Обозначение:r,|z|.

r z a b .
2
2

30. Модуль и аргумент комплексного числа.

M(a;b)

31. Пример. Найти модуль комплексных чисел:

Пример.
Найти
комплексных
модуль
чисел:
1) z 4 - 3i; 2) z -2 - 2i.
Решение.
1) a 4, b -3
r 4 ( 3)
2
25 5.
2
16 9

32.

2) a -2, b -2
r (-2) ( 2) 4 4
2
8 2 2.
2

33. Аргументом комплексного числа z≠0 называется угол , который образует вектор z с положительным направлением оси абсцисс.

Аргументом комплексного числа z≠0
называется угол , который образует
вектор
z
с
положительным
направлением
оси
абсцисс.
Обозначение: ,argz.
a
b
cos , sin .
r
r

34. Модуль и аргумент комплексного числа.

M(a;b)

35.

a
b
Из соотношени й cos , sin
r
r
следует a r cos и b r sin .
Если в запись комплексного числа
z вместо a и b подставить эти
значения, то получим :
z a bi rcos isin
r(cos isin ).

36. Запись комплексного числа в виде

Запись
виде
комплексного
числа
в
z r(cos i sin )
называется тригонометрической
формой комплексного числа.

37. Тригонометрическая форма комплексного числа

z r cos i sin
где φ – аргумент комплексного числа,
r=
a 2 b 2 - модуль комплексного числа,
cos
a
a2 b2
и sin
b
a2 b2

38.

Если
комплексному
числу
z cos isin , модуль которого
равен 1, поставить в соответствие
i
показательное выражение e , то
получим соотношение cos isin e ,
i
которое называется формулой Эйлера.

39.

Действия над комплексными
числами.

40. Арифметические операции над комплексными числами

(а + bi) + (c + di) = (а + с) + (b + d)i
(а + bi) - (c + di) = (а - с) + (b - d)i
(а + bi)·(с + di) = (ac - bd) + (ad + bc)i
a bi (a bi)( c di) ac bd bc ad
2
2
i
2
2
c di (c di)( c di) c d
c d

41. Сопряженные комплексные числа

Определение: Если у комплексного числа сохранить
действительную часть и поменять знак у мнимой части,
то получится комплексное число, сопряженное данному.
Если данное комплексное число обозначается буквой z,
то сопряженное число обозначается
:
z x yi z x yi
z
Из всех комплексных чисел действительные числа (и только они)
равны своим сопряженным числам.
Числа a + bi и a - bi называются взаимно сопряженными
комплексными числами.

42.

Действия над комплексными числами
Действия
над
комплексными
алгебраической форме
числами,
заданными
в
Сложение комплексных чисел
Суммой двух комплексных чисел z1=x1+y1i и z2=x2+y2i называется
комплексное число, определяемое равенством
z1+z2=(x1+x2)+i(y1+y2).
Свойства операции сложения:
1. z1+z2= z2+z1,
2. (z1+z2)+z3=z1+(z2+z3),
3. z+0=z.
Вычитание комплексных чисел
Вычитание определяется как действие, обратное сложению.
Разностью двух комплексных чисел z1=x1+y1i и z2=x2+y2i называется
такое комплексное число z, которое, будучи сложенным с z2, дает число z1 и
определяется равенством
z=z1 – z2=(x1 – x2)+i(y1 – y2).
содержание

43.

Умножение комплексных чисел
Произведением комплексных чисел z1=x1+y1i и z2=x2+y2i называется
комплексное число, определяемое равенством
z=z1 z2=(x1 x2 –y1 y2 )+i(x1 y2 –x2 y1 ).
Отсюда, в частности, следует важнейшее соотношение
i2= – 1.
Свойства операции умножения:
1. z1z2= z2z1,
2. (z1z2)z3=z1(z2z3),
3. z1(z2+z3 ) =z1z2+z1z3,
4. z∙1=z.
содержание

44.

Деление комплексных чисел
Деление определяется как действие,
обратное умножению. z1
z2
z,
Частным двух комплексных чисел
z1 и
z2≠0 называется комплексное число z, которое
будучи умноженным на z2, дает число z1, т.е.
если z2 z = z1.
содержание

45.

Возведение
комплексного
числа,
заданного в алгебраической форме в n-ю
степень
Выпишем целые степени мнимой единицы:
i 3 i 2 i ( 1)i i,
i 4 i 3 i ( i)i i 2 ( 1) 1,
i 5 i 4 i 1 i i,
i 6 i 5 i i 2 1
содержание

46.

На практике вместо полученной формулы используют следующий прием:
умножают числитель и знаменатель дроби
z1
на число, сопряженное
z2
знаменателю («избавляются от мнимости в знаменателе»).
Пример 2. Даны комплексные числа 10+8i, 1+i. Найдем их сумму,
разность, произведение и частное.
Решение.
а) (10+8i)+(1+i)=(10+1)+(8+1)i=11+9i;
б) (10+8i)–(1+i) =(10–1)+(8–1)i=9+7i;
в) (10+8i)(1+i) =10+10i+8i+8i2=2+18i;
10 8i (10 8i)(1 i) 10 10i 8i 8i 2 18 2i
г)
9 i.
2
1 i
(1 i)(1 i)
1 i
2
содержание

47.

Абрахам де Муавр (1667 – 1754) – английский математик
французского происхождения.
Заслуги Муавра:
• открыл (1707) формулу Муавра для возведения в степень (и извлечения
корней) комплексных чисел, заданных в тригонометрической форме;
• первый стал использовать возведение в степень бесконечных рядов;
• большой вклад в теорию вероятностей: доказал частный случаи теоремы
Лапласа, провёл вероятностное исследование азартных игр и ряда
статистических данных по народонаселению.
Формулу
Муавра
можно
использовать
для
тригонометрических функций двойного, тройного и т.д. углов.
нахождения

48.

Теорема (формула Муавра).
Пусть z — любое отличное от нуля
комплексное число, п — любое целое число.
Тогда
z n r cos i sin r n cosn i sin n .
n