Случаи приведения и уравнения равновесия систем сил

1. СЛУЧАИ ПРИВЕДЕНИЯ И УРАВНЕНИЯ РАВНОВЕСИЯ СИСТЕМ СИЛ

ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
СТАТИКА
ЛЕКЦИЯ 5

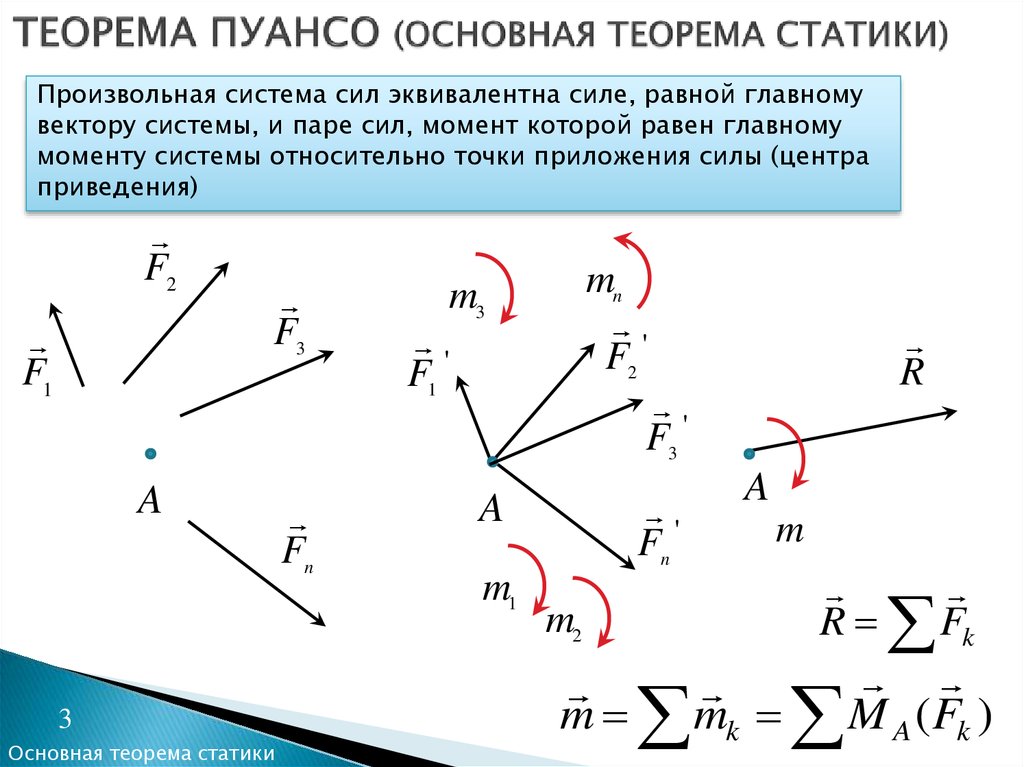
2. ТЕОРЕМА ПУАНСО (ОСНОВНАЯ ТЕОРЕМА СТАТИКИ)

Произвольная система сил эквивалентна силе, равной главному
вектору системы, и паре сил, момент которой равен главному
моменту системы относительно точки приложения силы (центра
приведения)
Луи́ Пуансо́ (1777-1859) —
французский математик и механи
к, академик Парижской Академии
наук(1813); пэр Франции
(1846), сенатор (1852). Известен
своими трудами в области
геометрии и механики
Основная теорема статики

3. ТЕОРЕМА ПУАНСО (ОСНОВНАЯ ТЕОРЕМА СТАТИКИ)

Произвольная система сил эквивалентна силе, равной главному
вектору системы, и паре сил, момент которой равен главному
моменту системы относительно точки приложения силы (центра
приведения)
F2
F1
F3
A
3
Основная теорема статики
Fn
mn
F2 '
m3
F1 '
R
F3 '
Fn '
A
m1
A
m
R
m2
m
mk
Fk
M A ( Fk )

4. СТАТИЧЕСКИЕ ИНВАРИАНТЫ

Статические инварианты – характеристики системы сил, не
зависящие от центра приведения
Статические инварианты позволяют более детально ответить на
вопрос, к чему приводится система сил.
Первый статический инвариант – главный вектор системы
F2
F1
A
4
Случаи приведения
F3
Fn

5. СТАТИЧЕСКИЕ ИНВАРИАНТЫ

Главный момент не является статическим
инвариантом.
Как он зависит от центра приведения?
Fk
rk A
Определим момент одной из сил системы
r
A
MA
rk B
M A ( Fk ) rkA Fk ,
M B ( Fk ) rkB Fk
r AB
M A ( Fk ) rkA Fk (r rkB ) Fk
B
Главный момент системы
M A ( Fk )
rkA Fk
5
Случаи приведения
(r rkB ) Fk
r Fk rkB Fk M B
AB Fk
M A M B AB R

6. СТАТИЧЕСКИЕ ИНВАРИАНТЫ

M A M B AB R
Умножим равенство скалярно
на главный вектор системы
M A R M B R ( AB R) R
Последнее слагаемое равно нулю (почему?)
MA R MB R
Второй статический инвариант – скалярное произведение
главного вектора на главный момент
MB
6
Случаи приведения
MA
R

7. СТАТИЧЕСКИЕ ИНВАРИАНТЫ

MB
MA
R
M*
Получили альтернативное определение
Второй статический инвариант – минимальный главный момент
Как найти минимальный главный момент?
*
MA R M R
7
Случаи приведения
M A R M *R
MA R
*
M
R

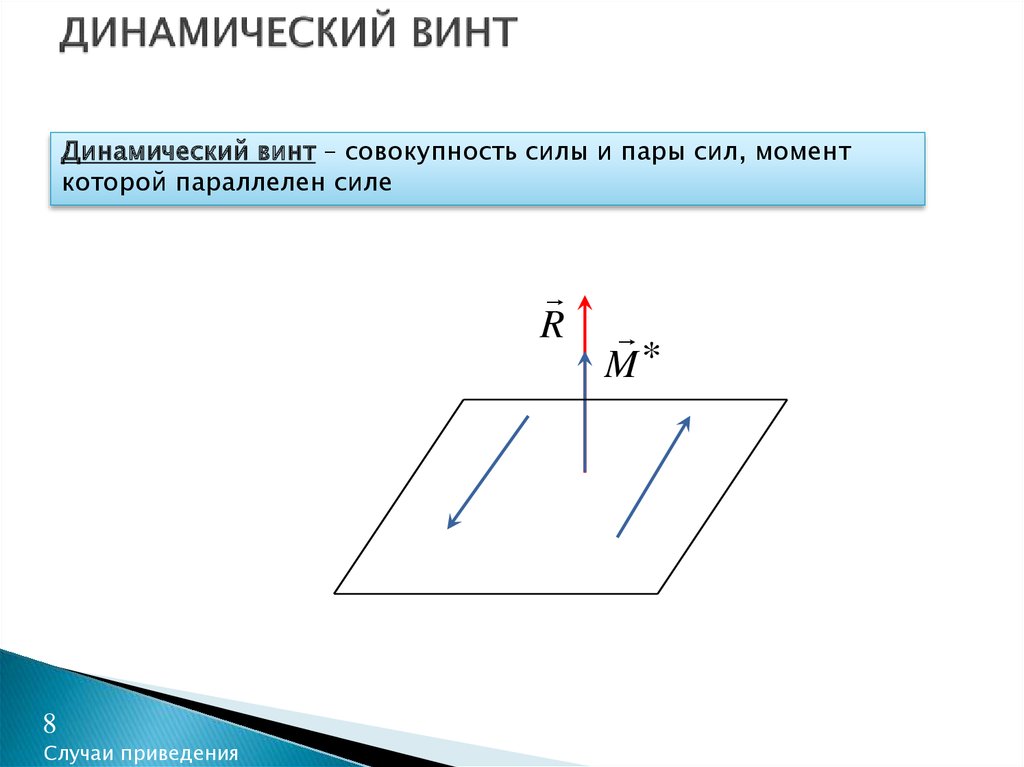
8. ДИНАМИЧЕСКИЙ ВИНТ

Динамический винт – совокупность силы и пары сил, момент
которой параллелен силе
R
8
Случаи приведения
M*

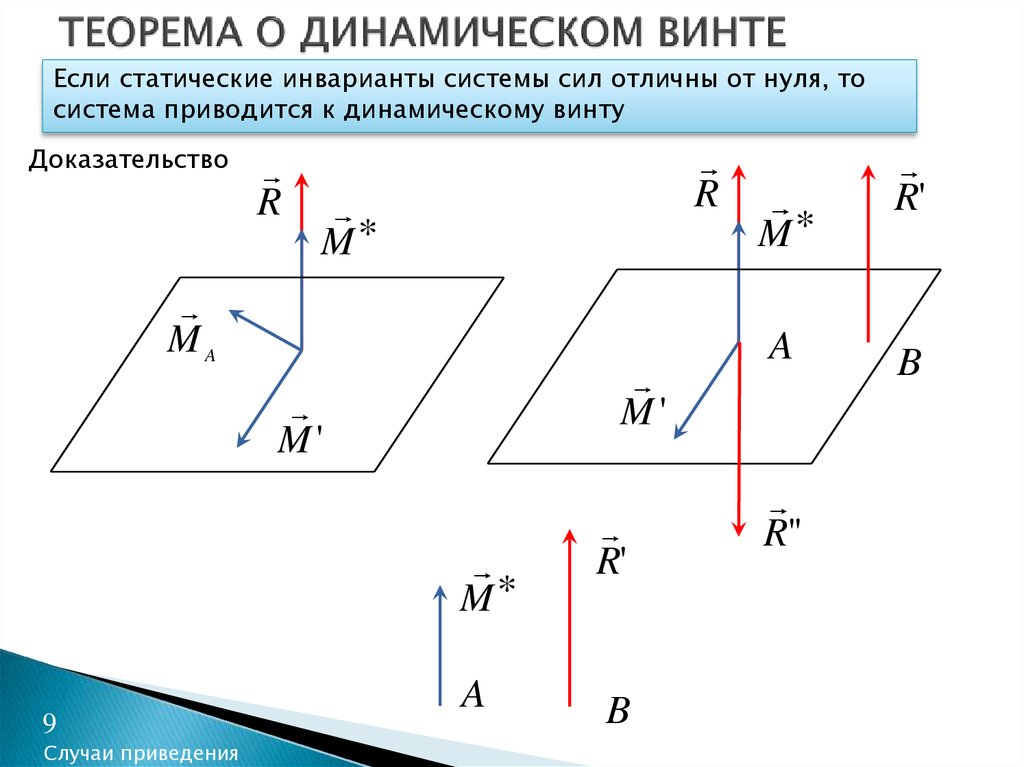
9. ТЕОРЕМА О ДИНАМИЧЕСКОМ ВИНТЕ

Если статические инварианты системы сил отличны от нуля, то
система приводится к динамическому винту
Доказательство
R
R
M*
MA
M'
M'
M*
9
Случаи приведения
A
R'
B
M*
A
R''
R'
B

10. СЛУЧАИ ПРИВЕДЕНИЯ СИСТЕМ СИЛ

M * 0,
M * 0,
M * 0,
M * 0,
10
R 0
R 0
R 0
R 0
Случаи приведения
динамический винт
равнодействующая
пара сил
система сил уравновешена

11. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛА

M * 0, R 0
R
Fk
система сил уравновешена
MO
M O ( Fk )
Rx Fkx
R Fk Rx i Ry j Rz k
M O M O ( Fk ) M x i M y j M z k
Mx
M O ( Fk ) x M O ( Fk ) x M x ( Fk )
11
Условия равновесия

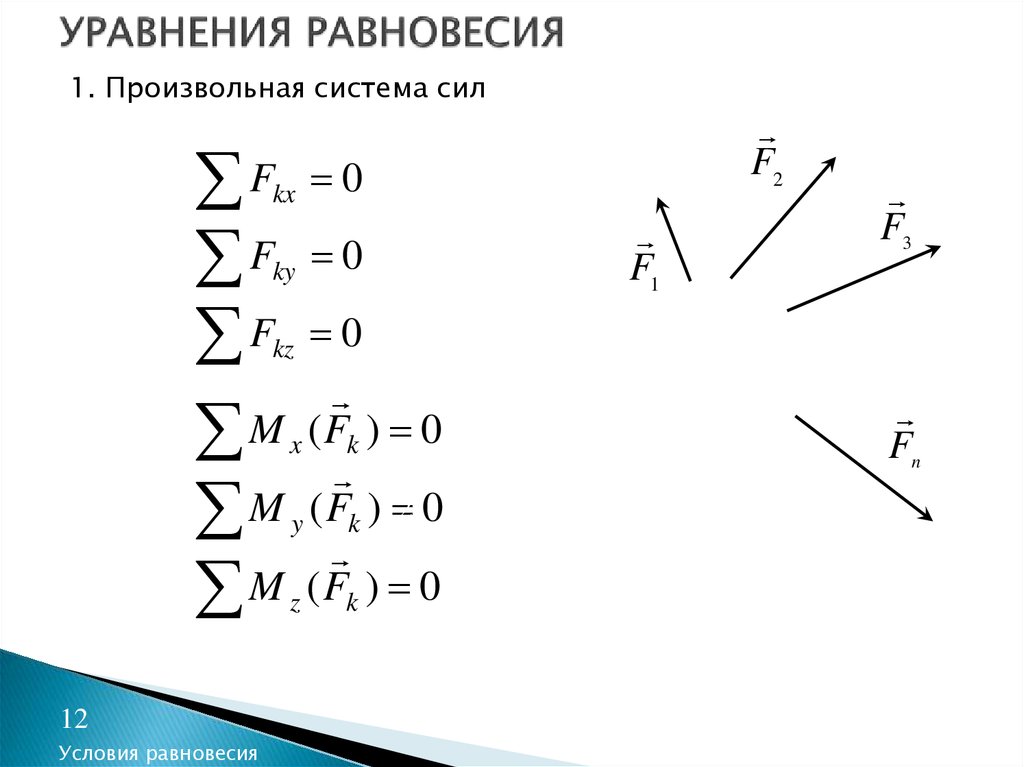
12. УРАВНЕНИЯ РАВНОВЕСИЯ

1. Произвольная система сил
F
F
F
M
M
M
kx
ky
F2
0
0
0
x ( Fk ) 0
12
y ( Fk ) 0
z ( Fk ) 0
F1
F3
kz
12
Условия равновесия
Fn

13. УРАВНЕНИЯ РАВНОВЕСИЯ

2. Система сходящихся сил
F
F
F
M
M
M
kx
0
ky
0
0
x ( Fk ) 0
13
y ( Fk ) 0
z ( Fk ) 0
F1
z
F2
kz
13
Условия равновесия
y
x
Fn

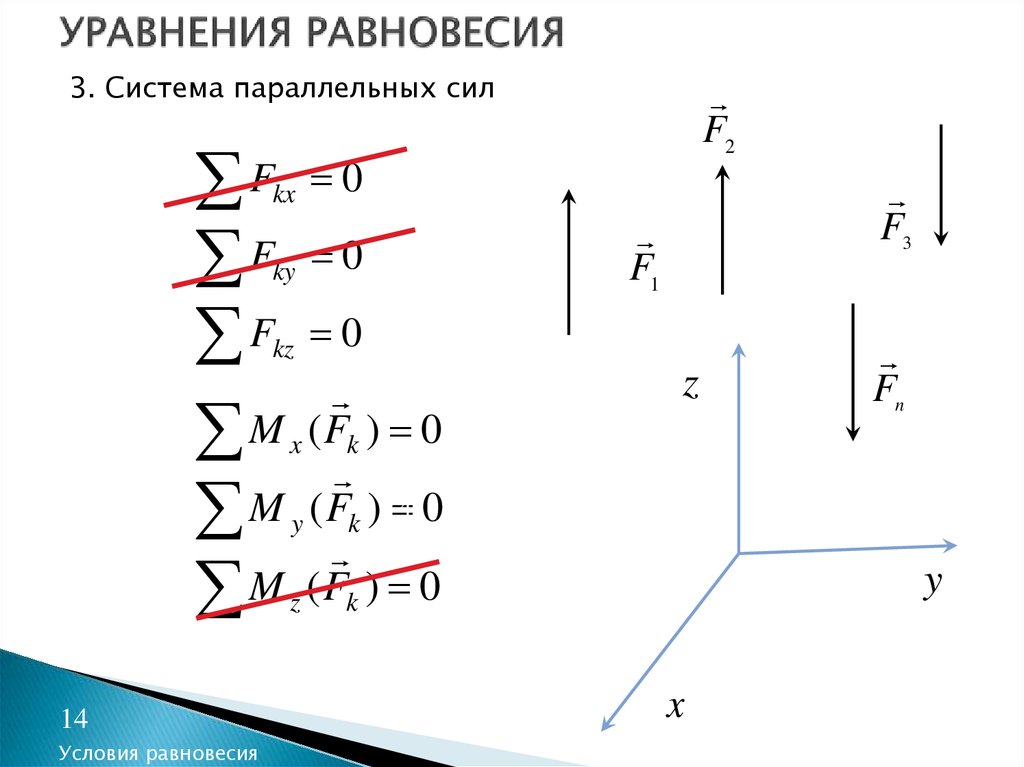
14. УРАВНЕНИЯ РАВНОВЕСИЯ

3. Система параллельных сил
F
F
F
M
M
M
kx
ky
F2
0
0
0
x ( Fk ) 0
14
y ( Fk ) 0
z ( Fk ) 0
F3
F1
kz
14
Условия равновесия
z
Fn
y
x

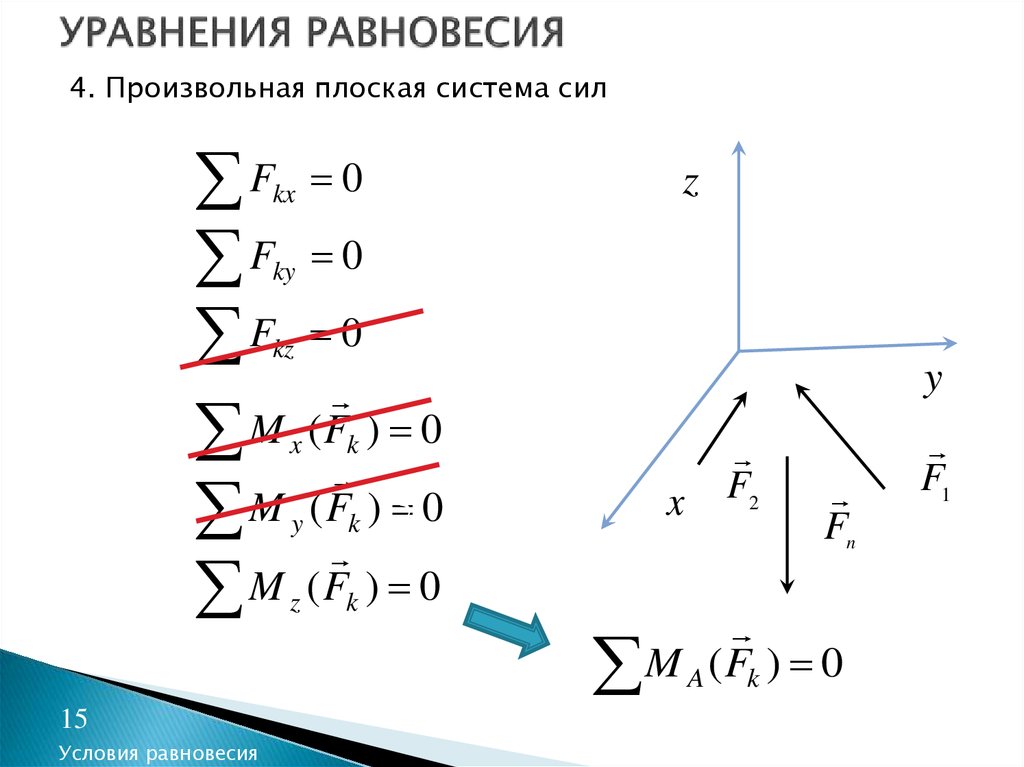
15. УРАВНЕНИЯ РАВНОВЕСИЯ

4. Произвольная плоская система сил
F
F
F
M
M
M
kx
0
ky
0
z
0
x ( Fk ) 0
15
y ( Fk ) 0
z ( Fk ) 0
kz
15
Условия равновесия
y
x
F2
Fn
M A ( Fk ) 0
F1

16. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА

Мосты
Опоры ЛЭП
Подъемные
краны
Металлические
каркасы зданий
16
Условия равновесия

17. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА

Ферма - жесткая, геометрически неизменяемая
конструкция, состоящая из стержней, соединенных
шарнирами.
Узел фермы –
точка крепления двух или
более стержней
A
1, 2, … 9 – стержни
17
Условия равновесия
C
1
4
E
3
5
6
2
8
B
7
D
A, B, … G – шарниры (узлы)
9
G

18. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА

YA
A
XA
RB
B
У статически определимых ферм число реакций опор
не более трех
Пусть k – число стержней, n – число узлов
Тогда ферма будет статически определимая при
выполнении равенства
k = 2n – 3
18
Условия равновесия

19. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА

Для расчета ферм необходимо
Найти реакции внешних опор с
использованием аксиомы отвердевания и
3-х уравнений равновесия
Определить усилия в стержнях фермы
методом вырезания узлов или
методом сечений ( Риттера)
19
Условия равновесия

20. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА

y
F3 III 6
5
4
F2 II 3
R 1
2
F1 BI
YA
IV
7
VI
8
V
A
9
1.Пронумеруем все стержни
X A фермы арабскими цифрами:
1, 2, 3, … 9
2. Пронумеруем узлы фермы
римскими цифрами:
I, II, III, … IV
x
B
3. Рассмотрим равновесие каждого из узлов и составим
уравнения равновесия (cчитаем условно все стержни
растянутыми).
Учитываем 3-й закон Ньютона: для каждого из стержней
усилия со стороны узлов равны по величине и направлены в
разные стороны.
20
Условия равновесия