Кодирование целых чисел

1. Кодирование целых чисел.

2.

Для работы с числами человек
использует в основном две формы для
их записи – естественную и
экспоненциальную.
Экспоненциальная форма записи чисел используется для
обозначения очень больших или очень маленьких чисел.
Например 0,000002=0,2*10-5 или 1000=103.

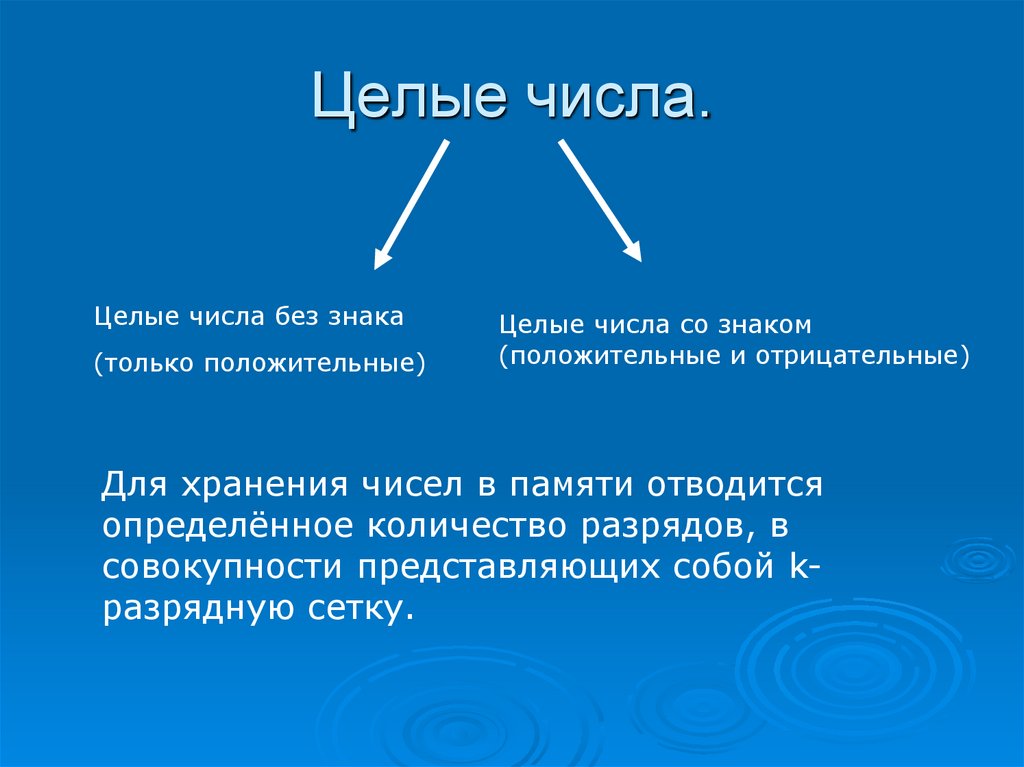
3. Целые числа.

Целые числа без знака
(только положительные)
Целые числа со знаком
(положительные и отрицательные)
Для хранения чисел в памяти отводится
определённое количество разрядов, в
совокупности представляющих собой kразрядную сетку.

4. Целые числа без знака.

Обычно занимают в памяти один или два
байта.
В однобайтовом формате значения от
000000002 до 111111112 (0…255)
Пример 7210=10010002
Биты числа
номера разрядов
0
1
0
0
1
0
0
0
7
6
5
4
3
2
1
0

5. Целые числа без знака.

В двухбайтовом формате значения
от 00000000 000000002
до 11111111 111111112
(0…65535)
Пример 7210=10010002
0
0
0
0
0
0
0
0
0
1
0
0
1
0
0
0
15 14 13 12 11 10
9
8
7
6
5
4
3
2
1
0

6. Целые числа со знаком.

Обычно занимают в памяти компьютера
1, 2 или 4 байта, при этом самый левый
(старший) разряд содержит
информацию о знаке числа. Знак «+»
кодируется 0, а «-» - 1

7. Целые числа со знаком.

В однобайтовом формате значения
от -128 до 127.
В двухбайтовом формате значения
От -32 768 до 32 767.
В четырёхбайтовом формате значения
от -2 147 483 648 до 2 147 483 647.

8. Целые числа со знаком.

Примеры.
110=12
0
0
0
Знак числа «+»
0
0
0
0
1

9. Целые числа со знаком.

В компьютерной технике применяются
три формы записи (кодирования) целых
отрицательных чисел: прямой код,
обратный код, дополнительный код.

10. Прямой код числа.

В знаковый разряд помещается цифра 1,
а в разряды цифровой части –
двоичный код его абсолютной
величины.
Пример
Прямой код числа -1:
1
0
0
Знак числа «-»
0
0
0
0
1

11. Обратный код числа.

Получается инвертированием всех цифр
двоичного кода абсолютной величины
числа, включая разряд знака: нули
заменяются единицами, а единицы –
нулями.
Пример
Число: -1.
Код модуля числа: 0 0000001.
Обратный код числа: 1 1111110.
1
1
1
1
1
1
1
0

12. Дополнительный код числа.

Получается образованием обратного
кода с последующем прибавлением
единицы к его младшему разряду.
Пример
Число: -1.
Код модуля числа: 0 0000001.
Обратный код числа: 1 1111110
+1
1 1111111
1
1
1
1
1
1
1
1

13. Как компьютер выполняет арифметические действия над целыми числами.

В большинстве компьютеров операция
вычитание не используется. Вместо неё
производится сложение уменьшаемого
с обратным или дополнительным кодом
вычитаемого. Это позволяет
существенно упростить конструкцию
АЛУ.

14. Примеры:

3
+
7
10
0 0000011
+
0 0000111
0 0001010
3
-10
-7
0 0000011
+
1 1110101
1 1111000
+
Обратный код числа -10
Обратный код числа -7

15. Примеры:

+
10
-3
7
0 0001010
+
1 1111100
0 0000110
Обратный код числа -3
+1
0 0000111
Компьютер исправляет полученный первоначально
неправильный результат (6 вместо 7) переносом
единицы из знакового разряда в младший разряд
суммы.

16. Примеры:

-3
+
-7
-10
1 1111100
+
1 1111000
1 1110100
+1
1 1110101
Обратный код числа -3
Обратный код числа -7
Обратный код числа -10
Полученный первоначально неправильный результат (обратный код
числа -11 вместо обратного кода числа -10) компьютер исправляет
переносом единицы из знакового разряда в младший разряд суммы.
При переводе результата в прямой код биты цифровой части числа
инвертируются: 1 0001010 = -10

17. Задание 1.

Представить число 21 в однобайтовой
разрядной сетке.

18. Задание 2.

Представить число 21 и -21 в
двухбайтовой разрядной сетке.

19. Кодирование вещественных чисел.

20.

Для представления вещественных чисел
(конечных и бесконечных десятичных
дробей) используют формат с
плавающей точкой (запятой).
Форма с плавающей точкой использует представление
вещественного числа R в виде произведения мантиссы m
на основание системы счисления р в некоторой целой
степени n, которую называют порядком:
R = m * рn
m – мантисса,
n – порядок,
p – основание системы.

21.

Например, число 25,324 можно записать в
таком виде: 0.25324х102.
Здесь m=0.25324 — мантисса,
n=2 — порядок. Порядок указывает, на какое
количество позиций и в каком направлении
должна «переплыть», т.е. сместиться
десятичная точка в мантиссе. Отсюда
название «плавающая точка».
Однако справедливы и следующие равенства:
25,324 = 2,5324*101 = 0,0025324*104 =
2532,4*102 и т.п.

22.

Получается, что представление числа в форме
с плавающей точкой неоднозначно?
Чтобы не было неоднозначности, в ЭВМ
используют нормализованное
представление числа в форме с
плавающей точкой. Мантисса в
нормализованном представлении должна
удовлетворять условию:
0,1p ≤ m < 1p.

23.

Иначе говоря, мантисса меньше единицы
и первая значащая цифра — не ноль.
Значит для рассмотренного числа
нормализованным представлением
будет: 25,324=0.25324 * 102.

24.

Пусть в памяти компьютера вещественное число
представляется в форме с плавающей точкой в
двоичной системе счисления (р=2) и занимает
ячейку размером 4 байта. В ячейке должна
содержаться следующая информация о числе:
знак числа, порядок и значащие цифры
мантиссы. Вот как эта информация
располагается в ячейке:
±машинный
порядок
1-й байт
МА
2-й байт
НТИС
СА
3-й байт 4-й байт
В старшем бите 1-го байта хранится знак числа. В этом разряде 0
обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта
содержат машинный порядок. В следующих трех байтах хранятся
значащие цифры мантиссы.

25.

Что такое машинный порядок?
В семи двоичных разрядах помещаются двоичные
числа в диапазоне от 0000000 до 1111111. В
десятичной системе это соответствует диапазону
от 0 до 127. Всего 128 значений. Знак порядка в
ячейке не хранится. Но порядок, очевидно, может
быть как положительным так и отрицательным.
Разумно эти 128 значений разделить поровну
между положительными и отрицательными
значениями порядка. В таком случае между
машинным порядком и истинным (назовем его
математическим) устанавливается следующее
соответствие:
Машинный
порядок
0
1
2
3
...
64
65
...
125
126 127
Математический
порядок
-64
-63
-62
-61
...
0
1
...
61
62
63
Если обозначить машинный порядок Мр, а математический — р, то связь
между ними выразится такой формулой:
Мр = р + 64.

26.

Итак, машинный порядок смещён
относительно математического на 64
единицы и имеет только положительные
значения. При выполнении вычислений с
плавающей точкой процессор это смещение
учитывает.
В двоичной системе счисления смещение:
Мр2 = р2+100 00002

27.

Теперь мы можем записать внутреннее представление
числа 25,324 в форме с плавающей точкой.
1)Переведем его в двоичную систему счисления с 24
значащими цифрами.
25,32410= 11001,01010010111100011012
2)Запишем в форме нормализованного двоичного
числа с плавающей точкой:
0,110010101001011110001101*10101
Здесь мантисса, основание системы счисления (210=102) и порядок
(510=1012)записаны в двоичной системе.
3) Вычислим машинный порядок.
Мр2 = 101 + 100 0000 = 100 0101.
4) Запишем представление числа в ячейке памяти.
31
порядок
мантисса
0
0 1 0 0 0 1 0 1 1 1 0 0 1 0 1 0 1 0 0 1 0 1 1 1 1 0 0 0 1 1 0 1
Знак числа

28.

Число в форме с плавающей точкой
занимает в памяти компьютера 4 байта
(число обычной точности) или 8 байт
(число двойной точности).
Мы рассмотрели пример представления
числа 25,324 обычной точности

29.

Для того, чтобы получить внутреннее
представление отрицательного числа
-25,324, достаточно в полученном выше
коде заменить в разряде знака числа 0
на 1.
1 1 0 0 0 1 0 1 1 1 0 0 1 0 1 0 1 0 0 1 0 1 1 1 1 0 0 0 1 1 0 1

30. Задание.

Представьте двоичное число -100,12 в
четырёхбайтовом формате.
Представьте число сначала в форме с
плавающей запятой.

31. Решение.

-100,12= -0,1001*211
Мантисса -0,1001
Порядок 11
Машинный порядок 11+100 0000=100011.
1 1 0 0 0 0 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0