Похожие презентации:
Высшая математика. Вебинар для студентов заочной формы обучения (дистанционная)
1.
Высшаяматематика
Вебинар для студентов заочной
формы обучения
(дистанционная)
2.
Преподаватель:Кузьмина Ольга Борисовна
Кафедра: Информационно-компьютерных технологий
KuzminaOB@edu.mubint.ru
Сайт:
https://mubint.sharepoint.com/kuzmina/
3.
Порядок изучения дисциплиныВид работы
Примерные сроки
Лекции
13.12.2016
17.12.2016
Практические занятия
11.01.2017
14.01.2017
18.01.2017
25.01.2017
Тестирование
Январь-февраль 2017
Закрытие дисциплины
28.02.2017
Форма контроля – экзамен, для специальности «Менеджмент» – зачет.
Экзамен/зачет проставляется по результатам практической работы и итогового
тестирования в AdobeConnect.
4.
Порядок изучения дисциплины5.
Порядок изучения дисциплиныАдрес ресурса:
http://connect.mubint.ru
6.
Работа на сайте преподавателя Кузьминой О.Б.:7.
Работа на сайте преподавателя Кузьминой О.Б.: Отчеты по практическимработам
8.
Работа на сайте преподавателя Кузьминой О.Б.: Ведомость БРС9.
Литература:1. Н.Ш. Кремер Высшая математика для экономистов: учебник для
студентов вузов, обучающихся по экономическим специальностям/Н.Ш.
Кремер. – М.: ЮНИТИ-ДАНА, 2003-2015 г.г.
2. Н.Ш. Кремер Высшая математика для экономистов: практикум, 2006 г.
3. Учебно-методическое пособие «Математика», МУБиНТ
Учебно-методические пособия, задания на практические занятия,
презентации с лекций-вебинаров и практических работ выложены на
сайте преподавателя Кузьминой О.Б. в разделе «Общие документы: /
Заочное (индивидуальное) обучение / Высшая математика».
10.
1. Матрицы иопределители
11.
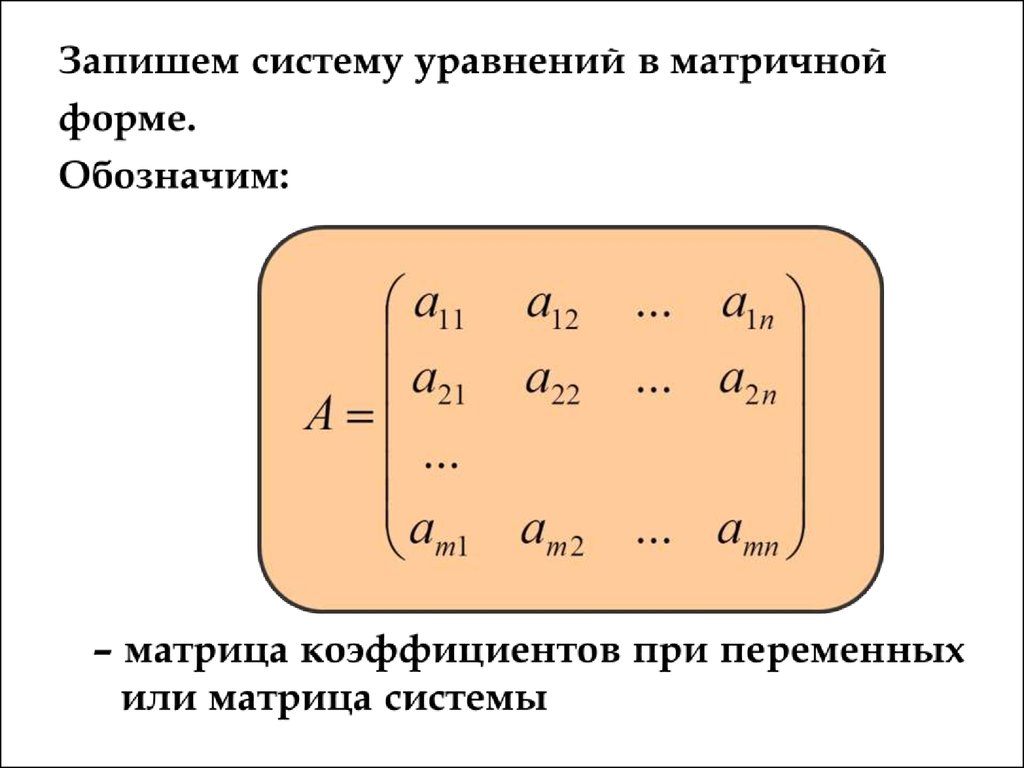
1.1. Матрицы и действия над нимиМатрицей размера m × n называется
прямоугольная таблица чисел,
содержащая m строк и n столбцов
Числа, составляющие матрицу,
называются элементами матрицы
12.
13.
Матрица размерности m × n14.
15.
Пример:16.
17.
Единичная матрица:18.
Нулевая матрица19.
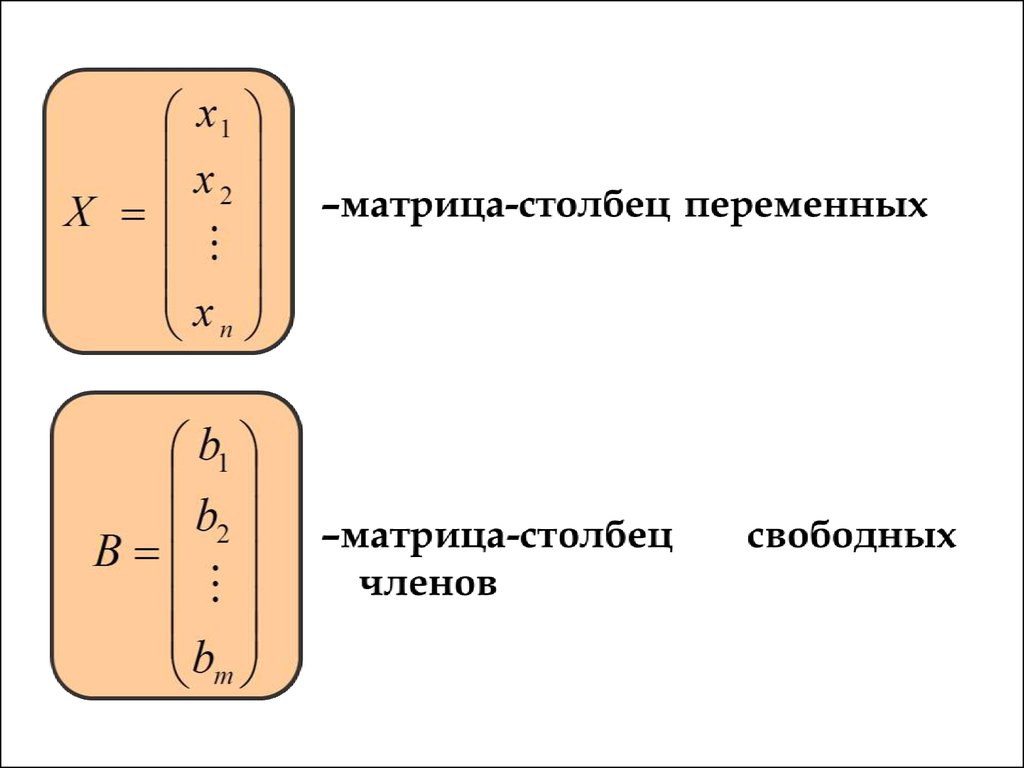
Матрица-строка20.
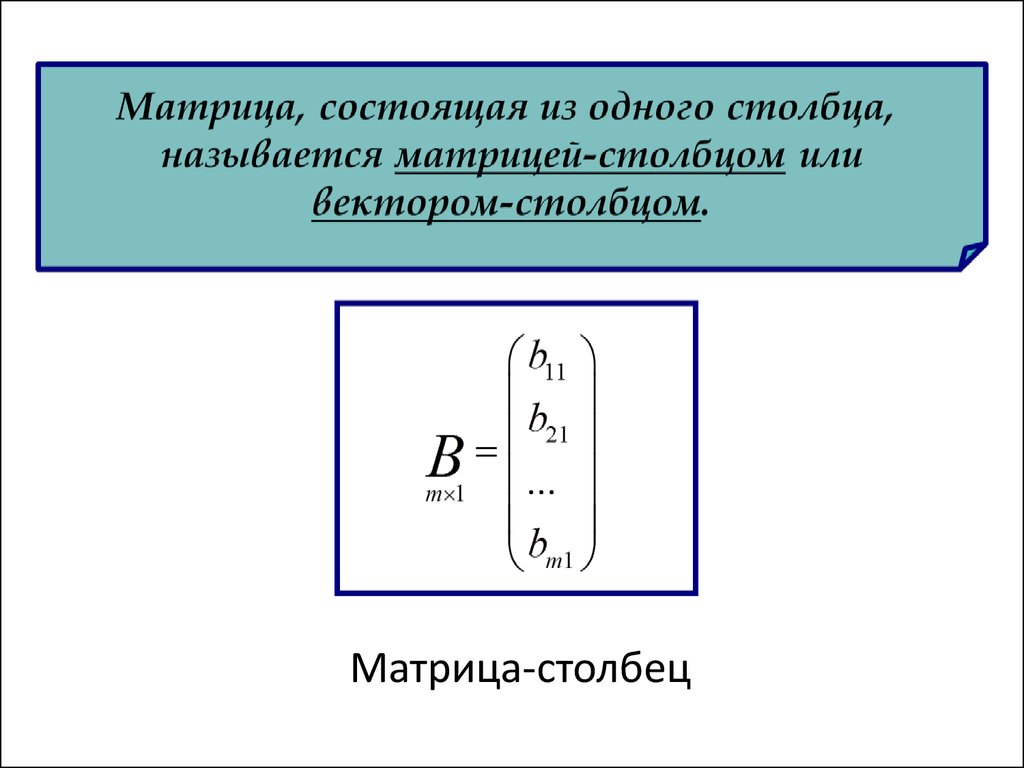
Матрица-столбец21.
22.
23.
1.2. Действия над матрицами1.2.1. Умножение матрицы на число
24.
25.
26.
1.2.2. Сложение матриц27.
28.
Пример:Найти сумму и разность матриц:
Решение:
29.
1.2.3. Умножение матриц30.
31.
Пример:Найти произведение матриц:
Решение:
32.
33.
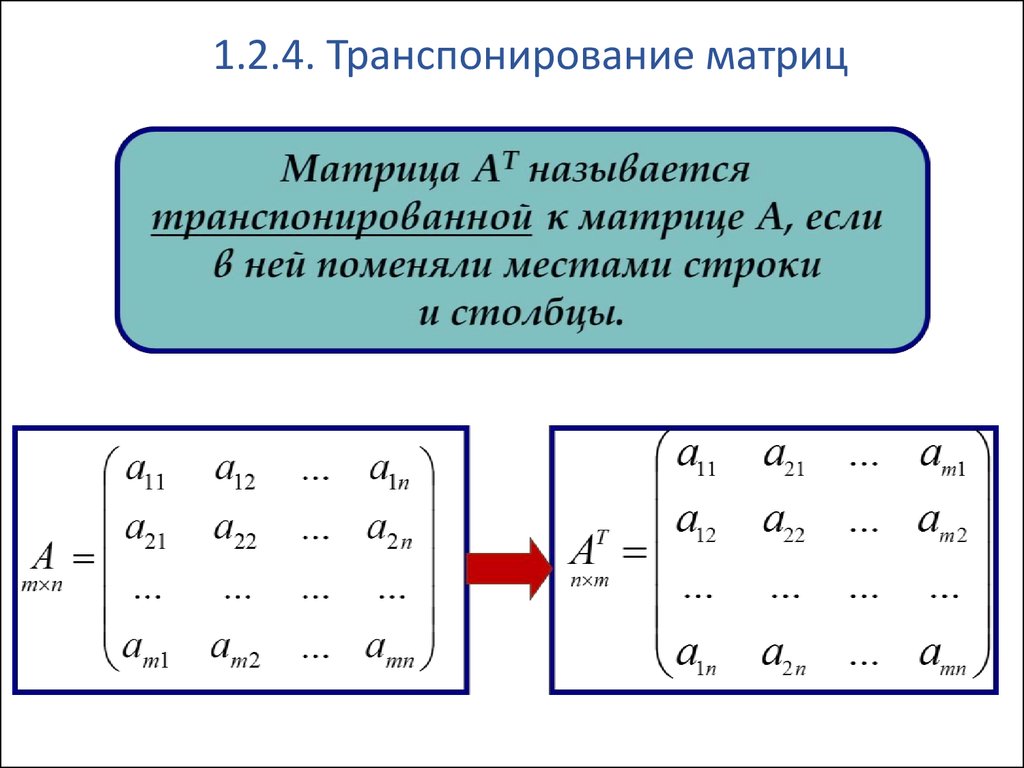
1.2.4. Транспонирование матриц34.
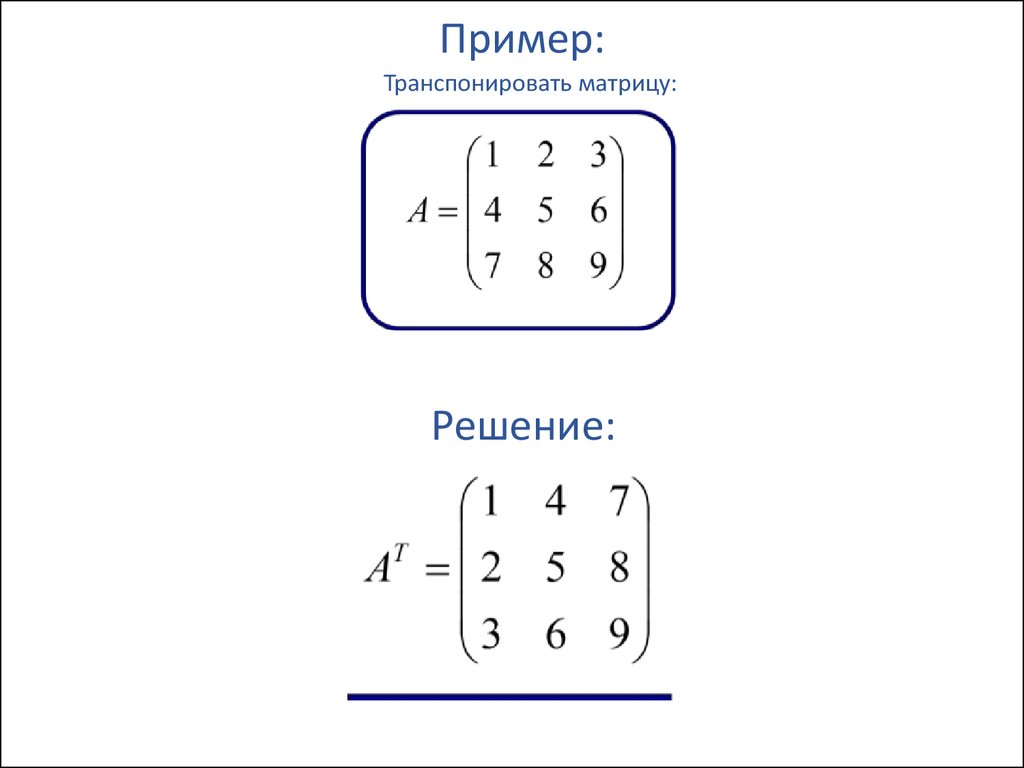
Пример:Транспонировать матрицу:
Решение:
35.
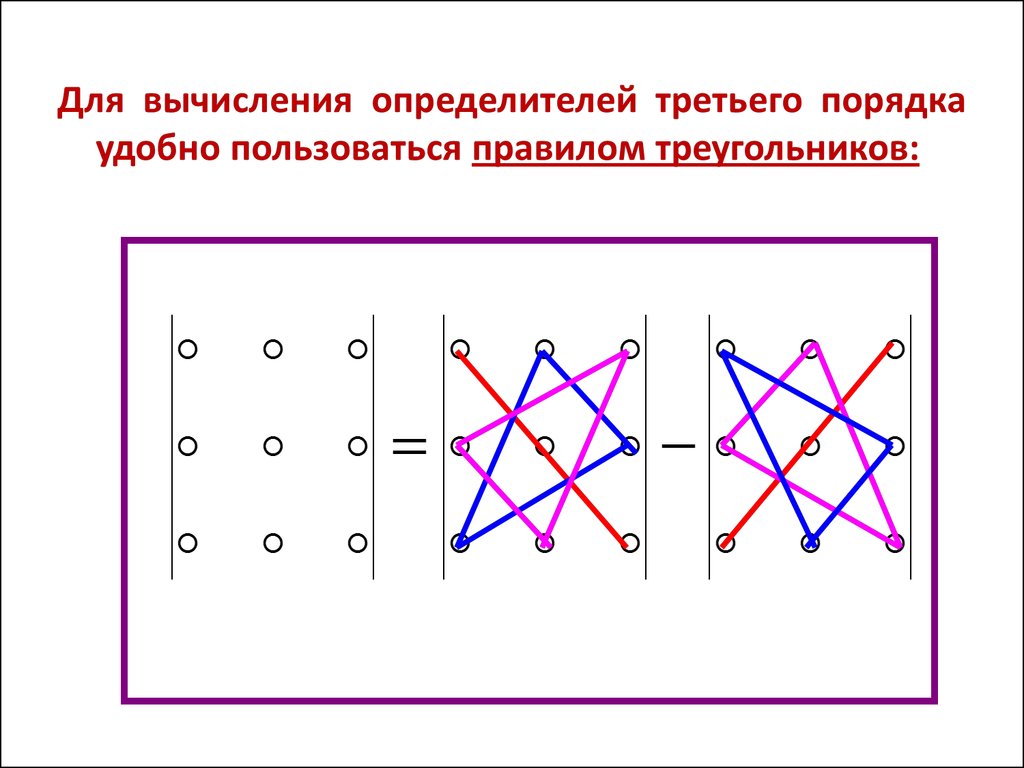
1.3. Определитель матрицы36.
37.
38.
39.
40.
Пример:Вычислить определители матриц:
Решение:
41.
42.
43.
44.
Свойства определителей:45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
Пример:Вычислить определитель:
56.
Решение:57.
58.
1.4. Обратная матрица59.
Алгоритм нахождения обратной матрицы:60.
61.
62.
63.
64.
65.
Пример:Найти матрицу, обратную к матрице:
66.
Решение:67.
68.
69.
70.
2. Системылинейных
алгебраических
уравнений
71.
2.1. Понятие системы линейных уравнений72.
73.
74.
75.
76.
77.
78.
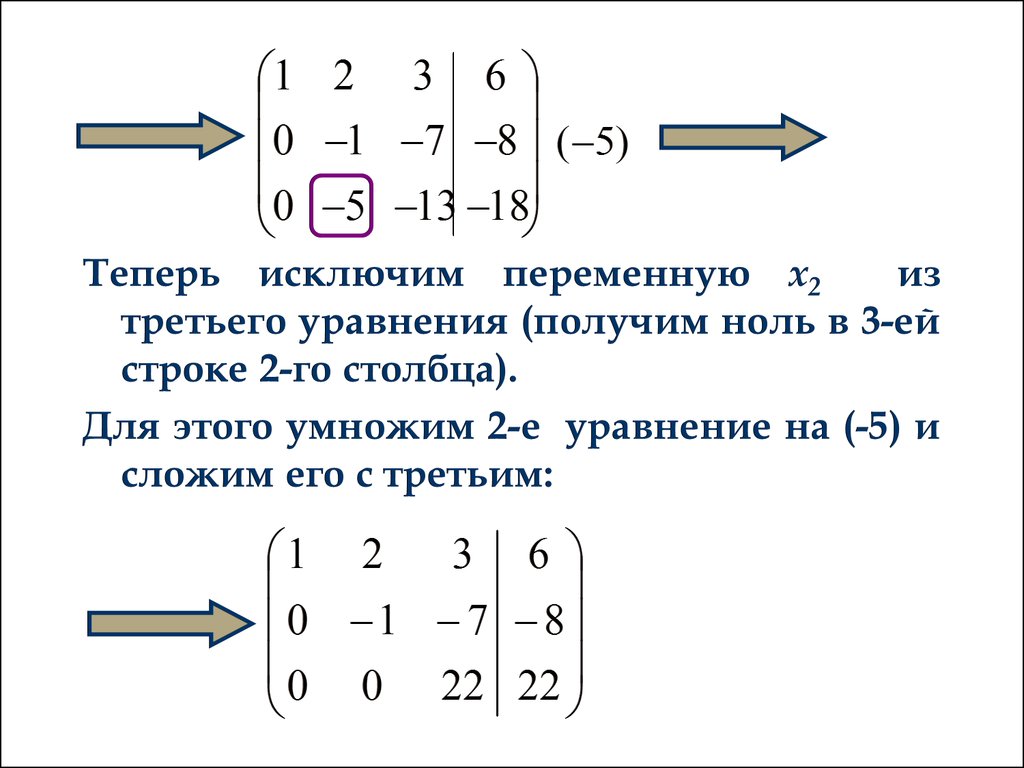
2.2. Решение систем линейных уравнений2.2.1. Метод Гаусса
79.
80.
81.
82.
83.
2.2.2. Метод Крамера84.
85.
Формулы Крамера86.
87.
88.
89.
90.
2.2.3. Метод обратной матрицы91.
92.
93.
94.
95.
96.
97.
3. Векторы идействия над
ними
98.
3.1. Векторы на плоскости и в пространстве99.
100.
101.
102.
103.
Условие коллинеарности векторов104.
105.
106.
107.
108.
109.
110.
111.
112.
Условие перпендикулярности векторов113.
4. Уравнениелинии
114.
4.1. Уравнение прямой на плоскости115.
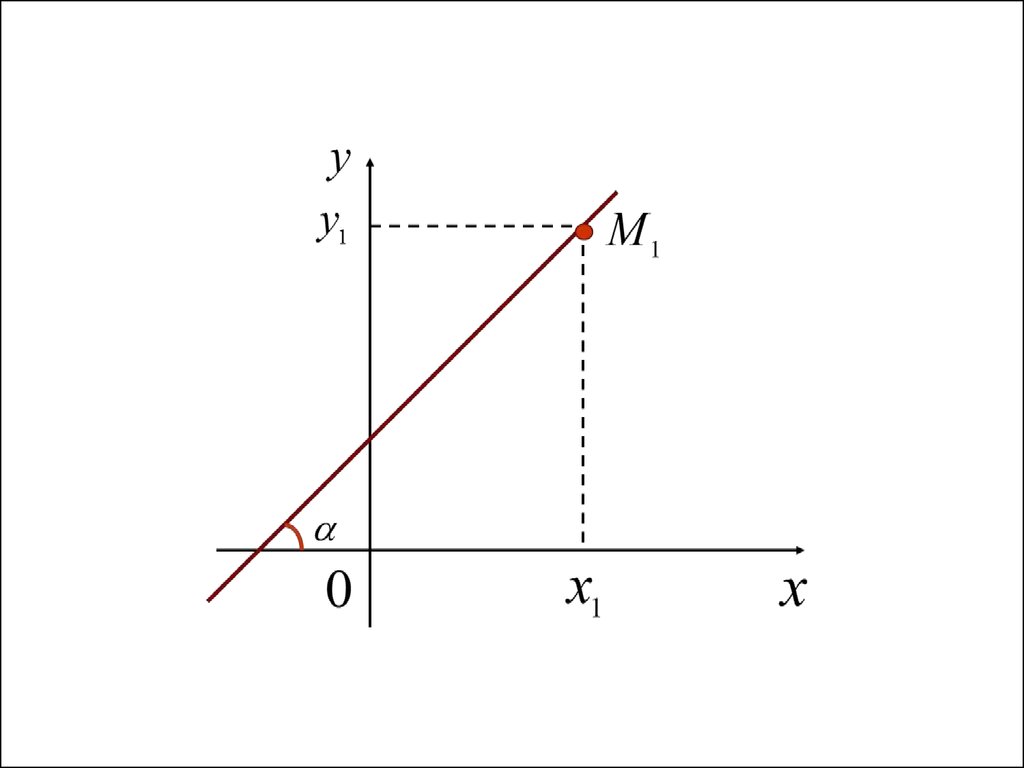
Способы задания прямой на плоскости1. Уравнение прямой с угловым
коэффициентом
116.
117.
Уравнение прямой с угловымкоэффициентом
118.
119.
120.
2. Уравнение прямой, проходящей череззаданную точку в заданном направлении
121.
122.
Уравнение прямой, проходящей череззаданную точку в заданном направлении
123.
124.
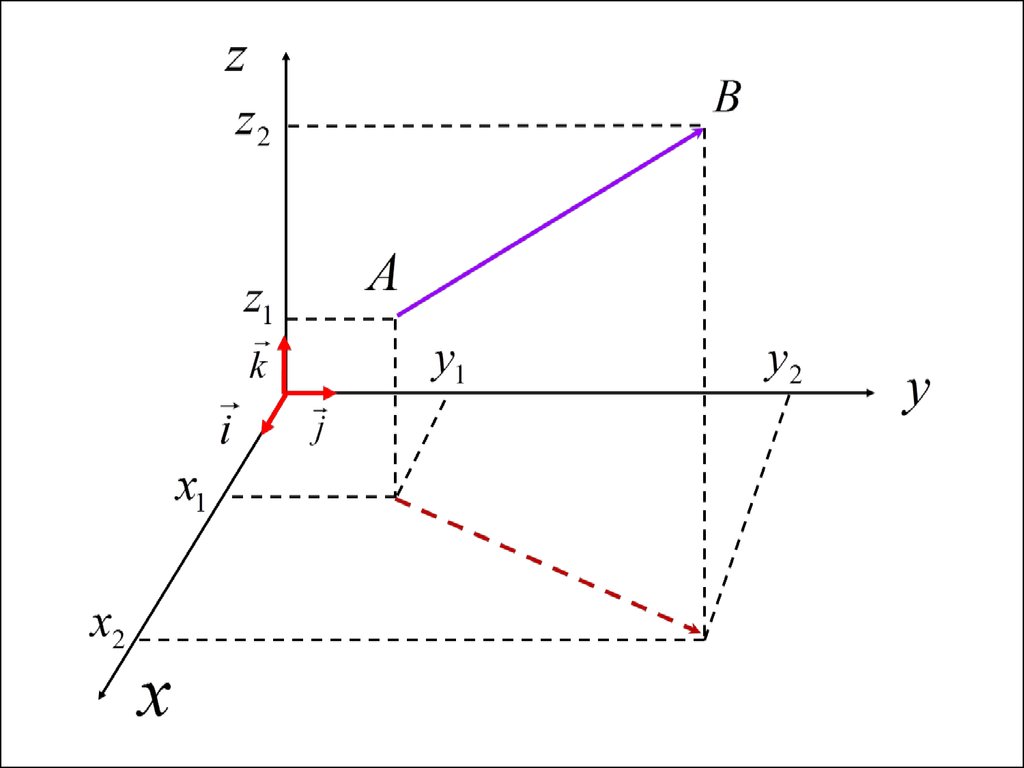
3. Уравнение прямой, проходящей через дветочки
125.
126.
Уравнение прямой, проходящей через дветочки
127.
128.
129.
4. Уравнение прямой в отрезках130.
131.
Уравнение прямой в отрезках132.
133.
134.
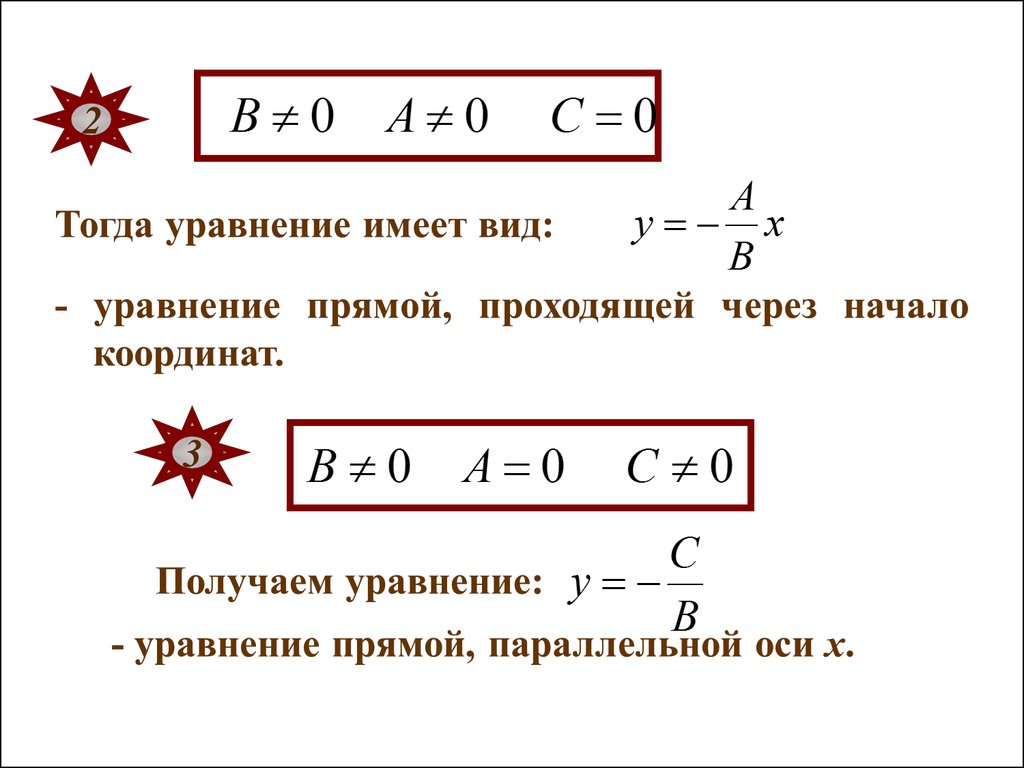
5. Общее уравнение прямой135.
136.
137.
138.
Общее уравнение прямой139.
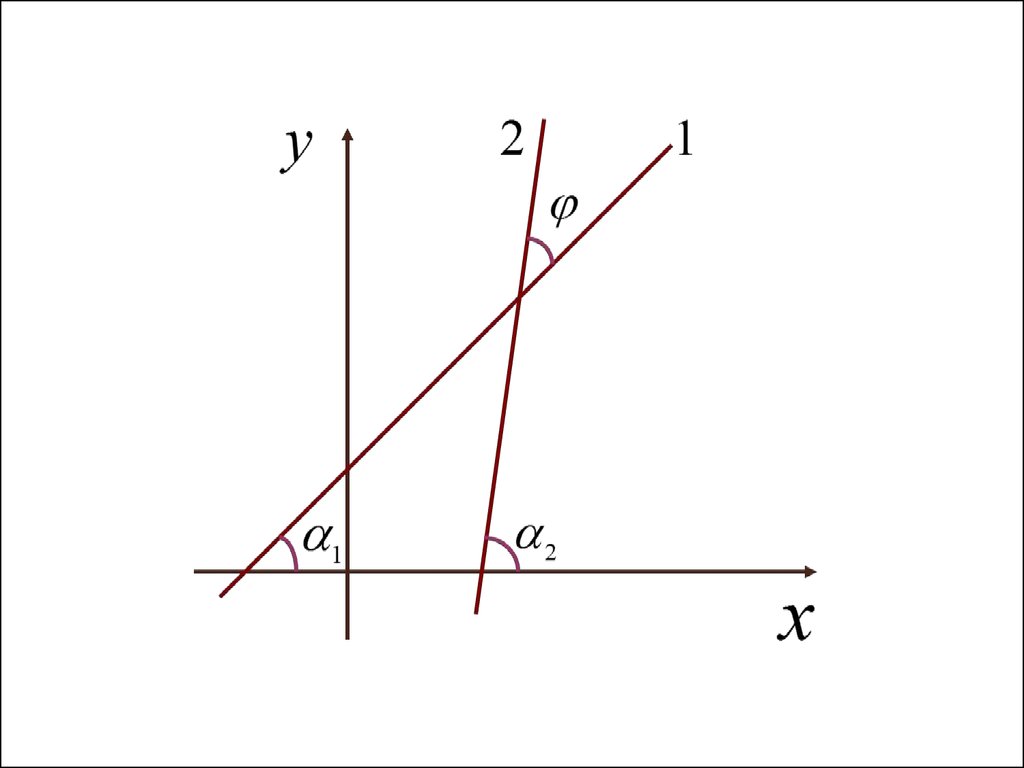
4.2. Условия параллельности иперпендикулярности прямых





























































































































































 Математика
Математика








