Высшая математика (практика)

1. Высшая математика (практика)

Кафедра
Информационно-компьютерных
технологий
Кузьмина Ольга Борисовна
[email protected]

2.

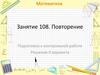
Порядок изучения дисциплины
Адрес ресурса:
http://connect.mubint.ru

3.

Работа на сайте преподавателя Кузьминой О.Б.: материалы для практических работ

4.

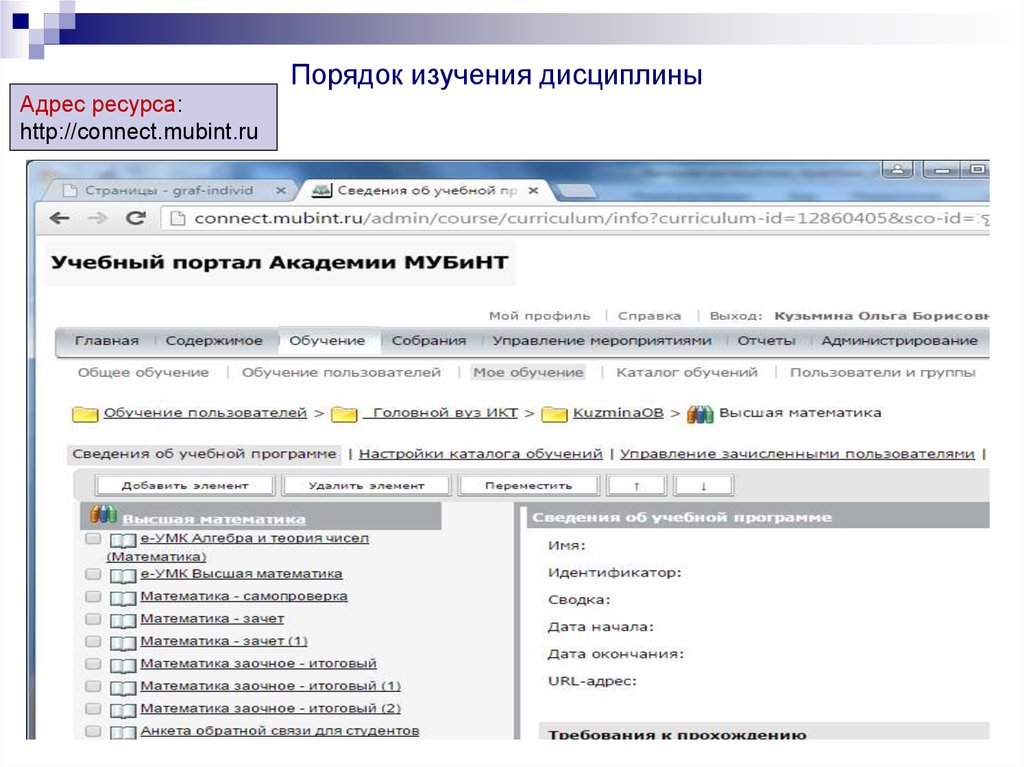
Работа на сайте преподавателя Кузьминой О.Б.: Отчеты по практическим работам

5.

Работа на сайте преподавателя Кузьминой О.Б.: Ведомость БРС

6.

Задание 1: Дана матрица С. Определить ранг матрицы С.
2
1
1
1
1
0
0
0
1 1 1 1
2 0 1 2
3 0 1
1
4 1 2 1
2 0 1 (1) * 2 (2) 1
1 1 1
0
3 0 1 (3) (1)
0
0
4 1 2 (4) (1)
2 0 1
1
1 0 0
0
5 1 3 (3) (2) * 5
0
6 1 3 (4) (2) * 6 0
2 0 1
5 1 3
1 0 0
6 1 3
2 0 1
1
1 0 0
0
0 1 3
0
0 1 3 (4) (3) 0
Rang С = 3
2 0 1
1 0 0
0 1 3
0 0 0

7.

Задание 2 (1): Дана квадратная матрица А третьего порядка. Вычислить
определитель матрицы А.
Определитель третьего порядка это число:
а11
а12
а13
а21 а22
а23 а11а22 а33 а21а32 а13 а12 а23а31 а13а22 а31 а23а32 а11 а12 а21а33
а31
а 33
а32
Например,
2 3 8
det A 1 0 5 2 0 6 1 7 8 3 5 4 8 0 4 5 7 2 1 3 6
4 7 6
0 56 60 0 70 18 28

8.

Задание 2 (2) : Найти матрицу А-1 .
Матрица А-1 называется обратной к матрице А, если выполняется условие
А· А-1= А-1·А=Е.
Теорема: Матрица А имеет обратную А-1 тогда и только тогда, когда А –
невырожденная, т.е. det A≠0.
Способ вычисления обратной матрицы с помощью алгебраических дополнений:
Алгоритм вычисления:
1) вычисляют определитель матрицы det A;
2) для каждого элемента aij вычисляют алгебраические дополнения Aij ;
~ из алгебраических дополнений:
3) составляют матрицу A
A11
~ A21
A
...
A
n1
4) транспонируют матрицу
~
A
A11
~
A
A T 12
...
A
1n
A12
...
A22
...
...
...
An 2
...
A21
...
A22
...
A2 n
A1n
A2 n
...
Ann
An1
... An 2
... ...
... Ann
Матрица ~ T
A
1
~T
A
A
det A
1
5) определяют обратную матрицу по формуле:
называется
присоединенной
к матрице А;

9.

Задание 2 (2): Найти матрицу А-1 .
Найти матрицу, обратную к матрице
1)
2)
det A=0+20-6-0+20+8=42
A11
0 2
5
A12
A13
3)
2 1 4
A 1
0 2
3 5
8
8
0 10 10;
1
2
3
8
1
0
3 5
A21
(8 6) 2;
A22
5 0 5;
10 2 5
~
A 28 28 7 ;
2
8
1
1 4
5
2
8
4
3 8
A23
( 8 20) 28;
16 12 28;
2
1
3
5
(10 3) 7;
10 28 2
~T
A 2 28 8
5 7 1
4)
A31
1
4
0
2
A32
A33
2
4
1 2
2 1
1
0
2 0 2;
( 4 4) 8;
0 1 1.
5)
A 1
10 28 2
1
2 28 8
42
5 7 1

10.

Задание 2 (2): Найти матрицу А-1 .
Сделаем проверку, убедимся, что полученная матрица искомая:
(внимательно выполняйте операцию умножения матриц!)
2 1 4
10
1
1
A* A 1
0 2 * 2
42
3 5
8
5
28
28
7
2 1 0 0
8 0 1 0 E
1 0 0 1

11.

;
.
Задание
2 (3): Найти решение системы уравнений
Решим систему уравнений методом Гаусса:
A X B
x1 5 x 2 4 x3 16
3 x1 x 2 8
3 x 2 x x 11
2
3
1
Составим расширенную матрицу и приведем ее к ступенчатому виду:
4
16 1 5
4
16
1 5 4 16 1 5
3 1 0 8 0 14 12 40 0 14 12 40 .
3 2 1 11 0 13 11 37 0 0
2
2
Запишем эквивалентную ступенчатую систему:
x1 5 x 2 4 x3 16
14 х 2 12 x3 40;
2 x 2
3
x1 2
х 2 2.
x 1
3
Таким образом, решением данной системы уравнений является вектор
Х (2; 2; 1)

12.

Задание 3: Найти скалярное произведение (2a b , a b )
Пусть известны координаты векторов:
a (1,1, 2); b (2, 1,0)
Найдем координаты
c 2a b
и
d a b
c 2 (1,1, 2) (2, 1,0) (2,2, 4) (2, 1,0) (0,3, 4)
d (1,1, 2) (2, 1,0) (3,0, 2)
(2a b , a b ) 0 * 3 3 * 0 ( 4) * ( 2) 8

13.

Задание 4: При каком значении
(перпендикулярны)?
векторы c a b
и
d a b ортогональны
Пусть известны координаты векторов:
a (1,1, 2); b (2, 1,0)
Найдем координаты
c a b
и
d a b
c a b (1,1, 2) (2, 1,0) ( 1,2, 2)
d a b (1,1, 2) (2, 1,0) ( 2, 1, 2 )
Условие ортогональности полученных векторов:
(a b )( a b ) 0
( 1) * ( 2) 2 * ( 1) ( 2) * ( 2 ) 0
2 2 2 4 0
5 4 0
4
5

14.

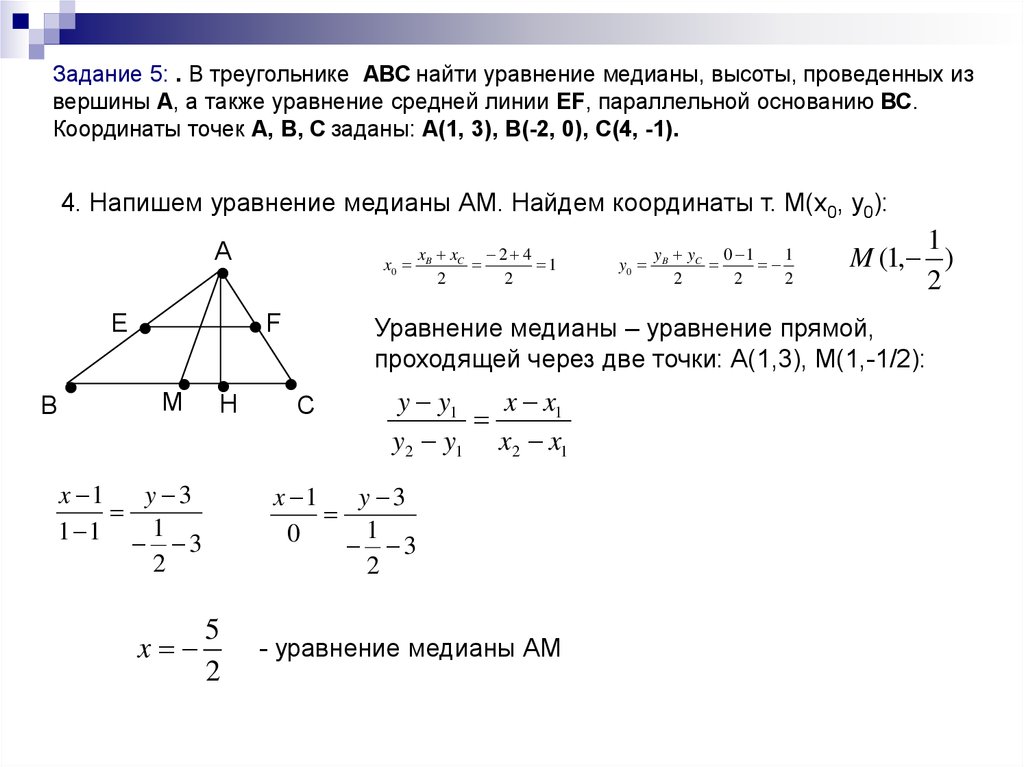
Задание 5: . В треугольнике АВС найти уравнение медианы, высоты, проведенных из
вершины А, а также уравнение средней линии EF, параллельной основанию ВС.
Координаты точек А, В, С заданы: А(1, 3), В(-2, 0), С(4, -1).
1. Найдем координаты точек E и F – середины отрезков АВ и АС:
А
E
В
(1 ( 2) 3 0
1 3
Е :
;
E
;
2
2
2 2
F
M
H
1 4 3 ( 1)
5
F :
;
F ;1
2
2
2
С
Уравнение прямой EF по двум точкам:
1
x y 3
2
2
3
5 1
1
2
2 2
1
3
y
2
2
1
3
2
x
y y1
x x1
y2 y1 x2 x1
1
2 2y 3
3
1
x
1
17
y x
6
12
Уравнение средней линии

15.

Задание 5: . В треугольнике АВС найти уравнение медианы, высоты, проведенных из
вершины А, а также уравнение средней линии EF, параллельной основанию ВС.
Координаты точек А, В, С заданы: А(1, 3), В(-2, 0), С(4, -1).
2. Напишем уравнение ВС по двум точкам:
А
E
В
x ( 2) y 0
4 ( 2) 1 0
F
M
H
y y1
x x1
y2 y1 x2 x1
x 2 y
6
1
6 y x 2
1
1
y x
6
3
С
1
Угловой коэффициент K ВС 6
Т.к. ВС ┴ АН, то КВС * КАН = -1;
K АН
1
6
1
6
Тогда уравнение прямой АН с угловым коэффициентом КАН =6
и проходящем через точку А(1,3) имеет вид: y y K ( x x )
0
y 3 6( x 1)
y 6x 3
0
- Уравнение высоты АН треугольника

16.

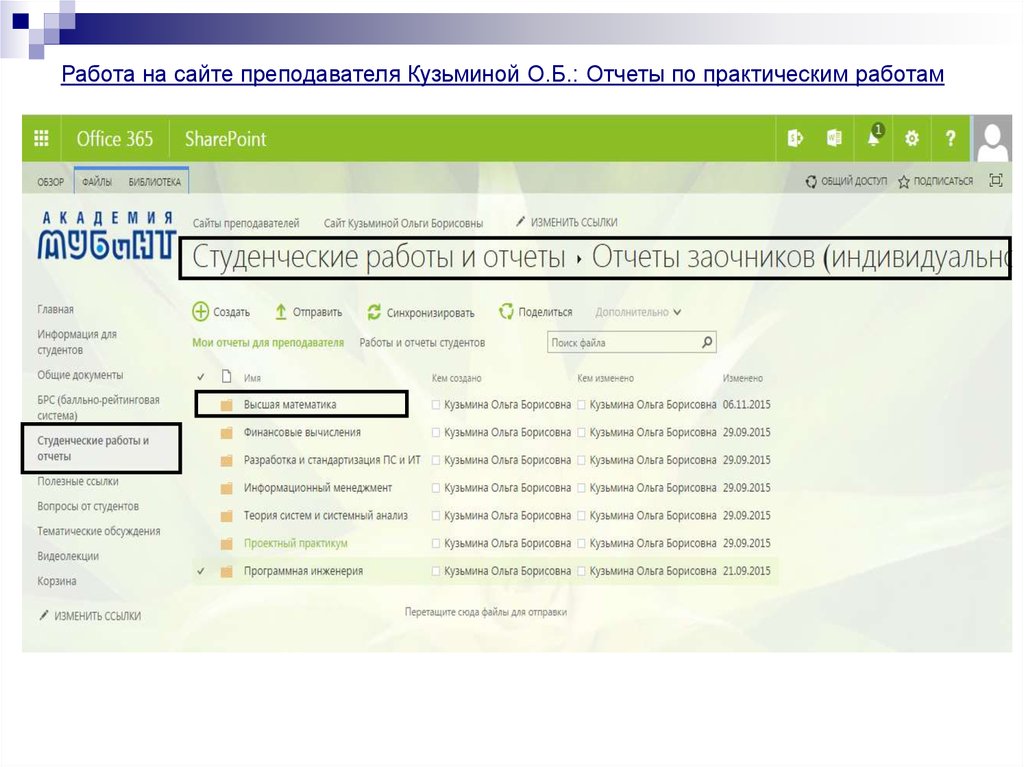
Задание 5: . В треугольнике АВС найти уравнение медианы, высоты, проведенных из
вершины А, а также уравнение средней линии EF, параллельной основанию ВС.
Координаты точек А, В, С заданы: А(1, 3), В(-2, 0), С(4, -1).
3. Найдем длину высоты АН. Это расстояние от т. А(1,3) до прямой ВС:
А
E
В
M
d
d
F
H
2
A2 B 2
С
1
1
*1 1* 3
6
3
1
2
1
6
Ax0 By 0 C
1 3 1
21
21
6
1
3
6
1 36
37
37
36 36
6
Длина высоты АН равна
21
37
1
1
y x
6
3
1
1
x y 0
6
3

17.

Задание 5: . В треугольнике АВС найти уравнение медианы, высоты, проведенных из
вершины А, а также уравнение средней линии EF, параллельной основанию ВС.
Координаты точек А, В, С заданы: А(1, 3), В(-2, 0), С(4, -1).
4. Напишем уравнение медианы АМ. Найдем координаты т. М(x0, y0):
А
E
В
x xC 2 4
x0 B
1
2
2
H
x 1
y 3
1 1 1 3
2
x
С
y y1
x x1
y2 y1 x2 x1
x 1
y 3
1
0
3
2
5
2
1
M (1, )
2
Уравнение медианы – уравнение прямой,
проходящей через две точки: А(1,3), М(1,-1/2):
F
M
y yC 0 1
1
y0 B
2
2
2
- уравнение медианы АМ

18.

Задание 6: . По каноническому уравнению кривой второго порядка определить тип
кривой. Найти координаты фокусов, вершин и центра.
Пример 1:
x2+y2-2x+4y-4=0
Сгруппируем по x, по y и выделим полные квадраты:
(x2-2x)+(y2+4y)-4=0
(x2-2x+1)+(y2+4y+4)-1-4-4=0
(x-1)2+(y+2)2=9
(x-1)2+(y+2)2=32
Это уравнение окружности с центром в т.(1, -2) и радиусом, равным 3.
Общее уравнение окружности: (x-a)2+(y-b)2=R2

19.

Задание 6: . По каноническому уравнению кривой второго порядка определить тип
кривой. Найти координаты фокусов, вершин и центра.
Пример 2:
x2+4y2-2x+56y+181=0
Сгруппируем по x, по y и выделим полные квадраты:
(x2-2x)+1+(4y2+56y)+196-16=0
(x-1)2+4(y+7)2=16
Общее уравнение эллипса:
x 1 2 4( y 7) 2
1
x 1 2 ( y 7) 2
1 - уравнение эллипса
16
4
2
4*4
2
2
x2 y2
2 1
2
a
b
Фокусы: F1 (-c, 0), F2 (c,0), где
c 42 22 12 3,5
c a 2 b2
Фокусы: F1 (-3,5 , 0), F2 (3,5 ,0)
Вершины: А1(4 , 0), А2(-4 ,0), В1(0, 2), В2(0, -2)
Центр: С(x0, y0) = C(1, -7)

20.

Задание 7: Найти пределы:
Основные свойства пределов:
1. Предел алгебраической суммы конченного числа переменных
величин равен алгебраической сумме пределов слагаемых:
lim(x + y + … + t) = lim x + lim y + … + lim t.
2. Предел произведения конечного числа переменных
величин равен произведению их пределов:
lim(x·y…t) = lim x · lim y…lim t.
3. Постоянный множитель можно выносить за знак
предела:
lim(cx) = lim c · lim x = c lim x.
Например, lim(5x + 3) = lim 5x + lim 3 = 5 lim x + 3.
4. Предел отношения двух переменных величин равен
отношению пределов, если предел знаменателя не равен нулю
5. Предел целой положительной степени переменной
величины равен той же степени предела этой же переменной.

21.

Задание 7: Найти пределы:
3x 5
x 7 x 5
1) lim
Т.к. функция непрерывна в т. x=7, то предел функции равен значению
функции в этой точке:
3x 5 3 * 7 5
lim
13
x 7 x 5
7 5

22.

Задание 7: Найти пределы:
sin x
0
x
x
2) lim
1
0
Т.к. отношение ограниченной функции sin x ( sin x 1)
к бесконечно большой величине x (при x ) есть
величина бесконечно малая

23.

Задание 7: Найти пределы:
2x2 x 1 0
3) lim
2
x 1
( x 1)
0
Разложим числитель на множители и сократим дробь на (x-1):
сокращение возможно, т.к. при x 1 (x-1) 0, но 0
1
2 x x 1
2
2x x 1 0
2x 1
2
lim
lim
lim
2
2
x 1
x 1 x 1
( x 1)
( x 1)
0 x 1

24.

Задание 7: Найти пределы:
2 x 3 3x 2 5 x 7
3 3 3
3
2 x 3 3x 2 5 x 7
2
x
x
x
x
4) lim 3
lim
2
x 3 x 4 x x 2
x 3 4 1 2
3
2
3
x x
x

25.

Задание 7: Найти пределы:

26.

Задание 8: Вычислите производную функции:
Таблица производных:
Правила дифференцирования:

27.

Задание 8: Вычислите производную функции. Примеры:
1) y x (1 x) ln(1 x)
1 x
y 1 (1 x) ln(1 x) (1 x)(ln(1 x)) 1 ln(1 x)
( 1) ln(1 x)
1 x
x
2) y
sin x cos x
x (sin x cos x) x(sin x cos x) sin x cos x x cos x x sin x
y
2
(sin x cos x)
(sin x cos x) 2

28.

Задание 8: Вычислите производную функции. Примеры:
3 2
x
3) y 5 ln x
Это произведение двух функций, каждая из которых – сложная функция
y 5u , где _ u x 3
y1 u12 , где _ u1 ln x
* ln
y 5
'
x3
'
2
'
x 5 * ln x
x3
2
5 * ln 5 * x ' * ln x 5 * 2 ln x * ln x '
x3
3
x3
2
1
2
x3
2
5 ln 5 * 3 x ln x 5 * 2 ln x * 5 ln x 3 ln 5 * x ln x
x
x
x3
2
2
x3

29.

Задание 9: Найти неопределенный интеграл.
Таблица неопределенных интегралов:
1. dx x C .
6. sin xdx cos x C .
x a 1
2. x dx
C, (a 1) .
a 1
dx
3. ln x C .
x
ax
x
4. a dx
C .
ln a
a
5. e x dx e x C .
11.
dx
arcsin x C .
1 x
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
14.
15.
2
dx
a x
2
arcsin
2
x
C ..
a
dx
1
x a
ln
C
x 2 a 2 2a x a
dx
a2 x2
1
a x
ln
C .
2a a x
7. cos xdx sin x C .
8.
dx
sin 2 x ctgx C .
dx
cos 2 x tgx C .
dx
arctgx C .
10.
1 x 2
dx
16.
ln x x 2 a C .
x2 a
9.
17. shxdx chx C .
18. chxdx shx C .
19.
dx
ch 2 x thx C .
20.
sh 2 x cthx C .
dx

30.

Задание 9: Найти неопределенный интеграл.Пример:
Пример . Вычислить cos 5xdx .
Решение. В таблице интегралов найдем
cos xdx sin x C .
Преобразуем данный интеграл к табличному,
воспользовавшись тем, что d ax adx .
Тогда:
d 5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5 x
5
5
1
= sin 5 x C .
5

31.

Задание 9: Найти неопределенный интеграл. Пример:
Пример. Вычислить x 3x x 1 dx .
Решение. Так как под знаком интеграла
находится сумма четырех слагаемых, то
раскладываем интеграл на сумму четырех
интегралов:
2
3
2 3x3 x 1 dx x 2 dx 3 x3dx xdx dx .
x
x4 x2
x3
x C
3
2
4
3

32.

Задание 9: Найти неопределенный интеграл. Пример:
t x 1
2x 1
2x 1
2t 1
x 2 2 x 1 dx ( x 1) 2 dx dt dx t 2 dt
x t 1
dt
1
1
2
2 t dt 2 ln t C 2 ln x 1
C
t
t
x 1

33.

Задание 9: Найти неопределенный интеграл. Пример (интегрирование по частям):
Формула интегрирования по частям:
udv
uv
vdu

34.

Задание 9: Найти неопределенный интеграл. Пример (интегрирование по частям):
(x
3
1) ln xdx
u ln x
dv ( x 1)dx
3
dx
du
x
4
x
v dv ( x 3 1)dx
x
4
4
4
dx
x
x
3
( x 1) ln xdx 4 x ln x 4 x x
x4
1 3
x ln x x dx dx
4
4
x4
x4
x ln x x C
16
4

35.

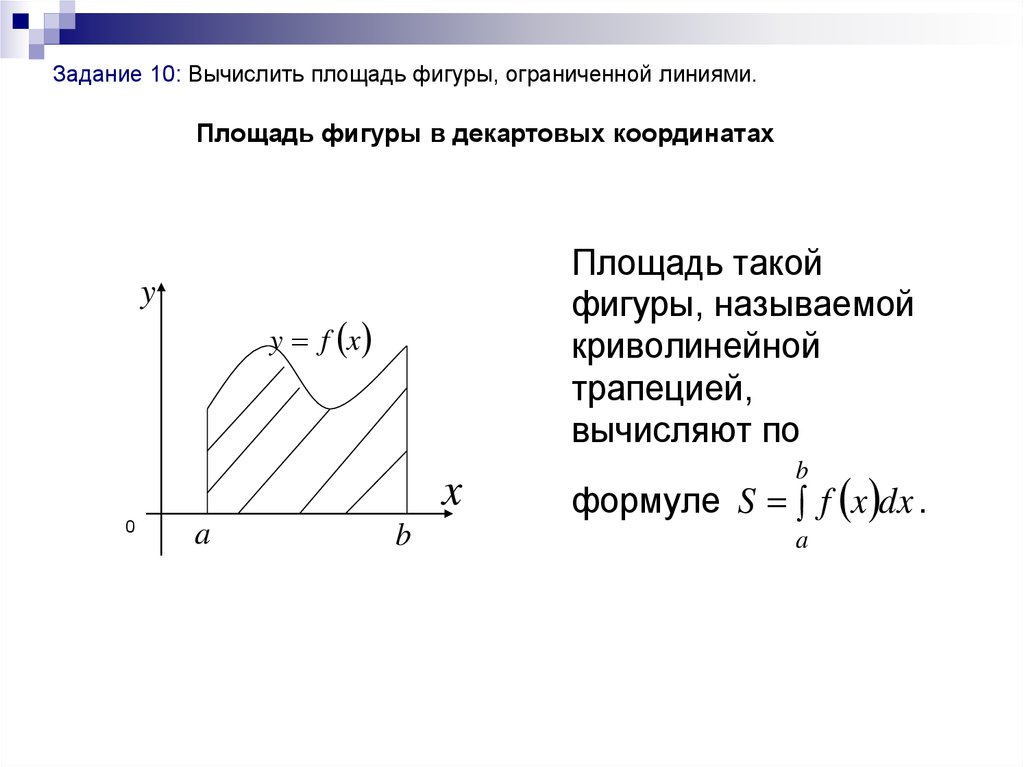
Задание 10: Вычислить площадь фигуры, ограниченной линиями.
Площадь фигуры в декартовых координатах
y
Площадь такой
фигуры, называемой
криволинейной
трапецией,
вычисляют по
y f x
x
0
a
b
b
формуле S f x dx .
a

36.

Задание 10: Вычислить площадь фигуры, ограниченной линиями.
Площадь фигуры, ограниченной графиками непрерывных
функций y f 1 x , y f 2 x , f1 x f 2 x и двумя прямыми
b
x a и x b определяется по формуле S f 2 x f1 x dx
a

37.

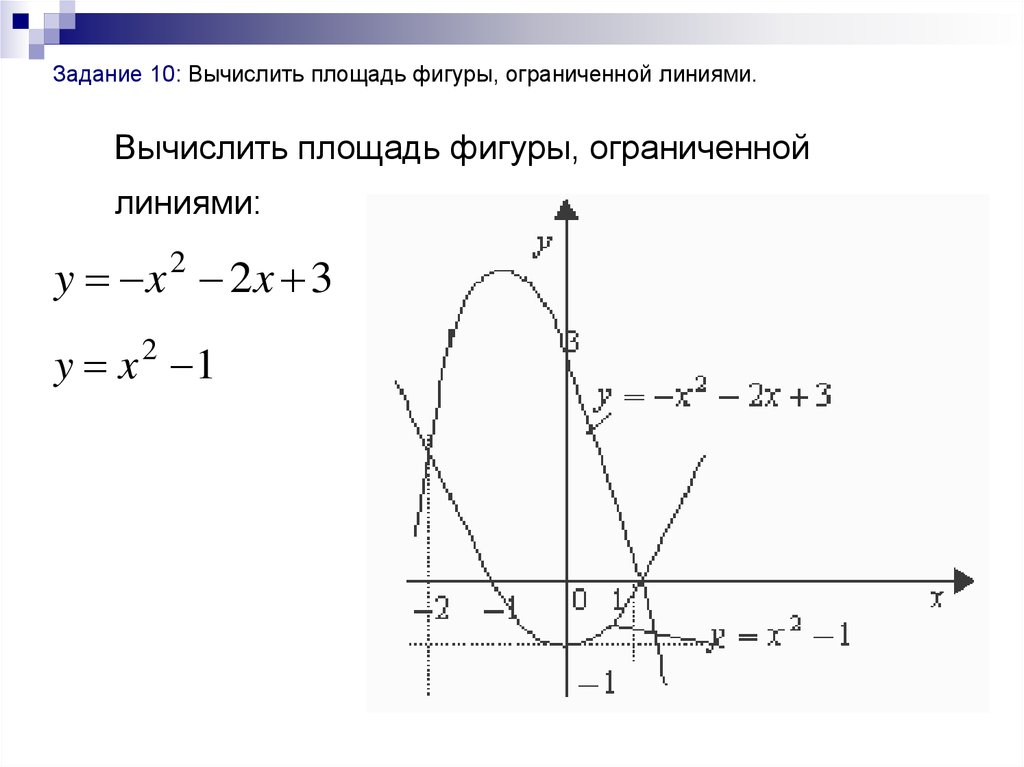
Задание 10: Вычислить площадь фигуры, ограниченной линиями.
Вычислить площадь фигуры, ограниченной
линиями:
y x 2x 3
2
y x 2 1

38.

Задание 10: Вычислить площадь фигуры, ограниченной линиями.
1
1
S x 2 x 3 x 1 dx 2 x 2 x 4 dx
2
2
2
2
2
1
3
2
x
x
2
2 x x 2 dx 2
2x
3
2
2
2
1
1 1 8 4
8
1 1
2 2 4 2 2 6
3
3 2
3 2 3 2
1
9
2 3 8 2 9
2
2

39. Спасибо за внимание! Жду Ваших вопросов…

контакт: Кузьмина Ольга Борисовна
e-mail: [email protected]
Успехов в изучении дисциплины!