Похожие презентации:
Резонанс в линейных электрических цепях
1.
РезонансРезонанс в линейных электрических цепях.
В электрических цепях иногда несмотря на наличие индуктивностей и
емкостей электрическая цепь ведет себя как активное сопротивление.
В такой электрической цепи напряжение на входе цепи совпадает по
фазе с током. Такое явление в электрической цепи называется
фазовым резонансом или просто резонансом.
Различают два вида резонанса:
1.Резонанс в последовательной цепи или резонанс напряжений.
Условия резонанса :
а) φu – φi = 0 или φ =0.
в )Jm( z ) 0
2003г.
Переменный ток
2.
Резонанс1.Резонанс в параллельной цепи или резонанс токов. Условия
резонанса :
а) φu – φi = 0 или φ =0.
в) Jm ( Y ) = 0
Резонанс в последовательной цепи или резонанс
напряжений.
i(t)
R
L
С
Z вх=R + jxL- jxc= R +j(xL- xc)=R + jx
u(t)
uR(t)
uL(t)
х
uC(t)
По условию резоанса Jm(Z)=0
2003г.
Переменный ток
3.
РезонансXL-Xc=0, или ХL=Xc
ХL=Xc
Условие резонанса в простых
последовательных цепях.
Пусть ω0 резонансная частота.
1
0L
0C
2 0 LC 1
0
Резонанс напряжений может быть достигнут 3 способами:
а) изменением частоты
в) изменением емкости
с) изменением индуктивности
2003г.
Переменный ток
1
LC
4.
РезонансВекторная диаграмма резонанса
напряжений
UL
UR=IR
UC
UR
UC=- IjXC
I
ULp Ix L I 0L
U Lp I
2003г.
UL= UC
UL=IjXL
1
0
U Lp
LC
L
C
1
L
I
L I
I
C
LC
- волновое сопротивление
Переменный ток
5.
Резонанс1
U c Ix c I
I
0c
1
1
C
L
I
I
C
LC
Uc I
U Lp I
U R IR
Если
>> R ,то UL=Uc>>UR. Так как при резонансе входное
напряжение уравновешивается напряжением на R , то UL=Uc>>Uвх
В режиме резонанса напряжение на емкости и индуктивности
может во много раз превосходить входное напряжение.
2003г.
Переменный ток
6.
РезонансЧастотные характеристики электрической цепи
при резонансе напряжений.
Z,
R,
X
Z(ω)
xL(ω)
φ
π/2
ω
R(ω)
ω0
ω
-π/2
Xc(ω)
Фазочастотная характеристика.
Частотные характеристики
сопротивлений
2003г.
Переменный ток
7.
РезонансРезонансные кривые последовательного
контура.
U,I
I
UL
Uc
I
U
ω
ω0
0
U
UL
I
c
Q
U
U
RI
R
2003г.
Q - коэффициент резонанса или
добротность контура.
Переменный ток
8.
РезонансI/Iр
Чем выше добротность, тем
острее резонансная кривая, тем
лучше избирательные свойства
цепи.
Q=0.5
1/ 2
Q=1.0
Q=10
ω* = ω/ωp
Полоса пропускания контура.
1
I/Iр
идеальная
Q
1/ 2
ω*
2003г.
ωH*
ωB*
Переменный ток
Полоса пропускания это
разность
верхней
и
нижней
частот,
между
которыми отнощение I/Ip
превышает 1 / 2
9.
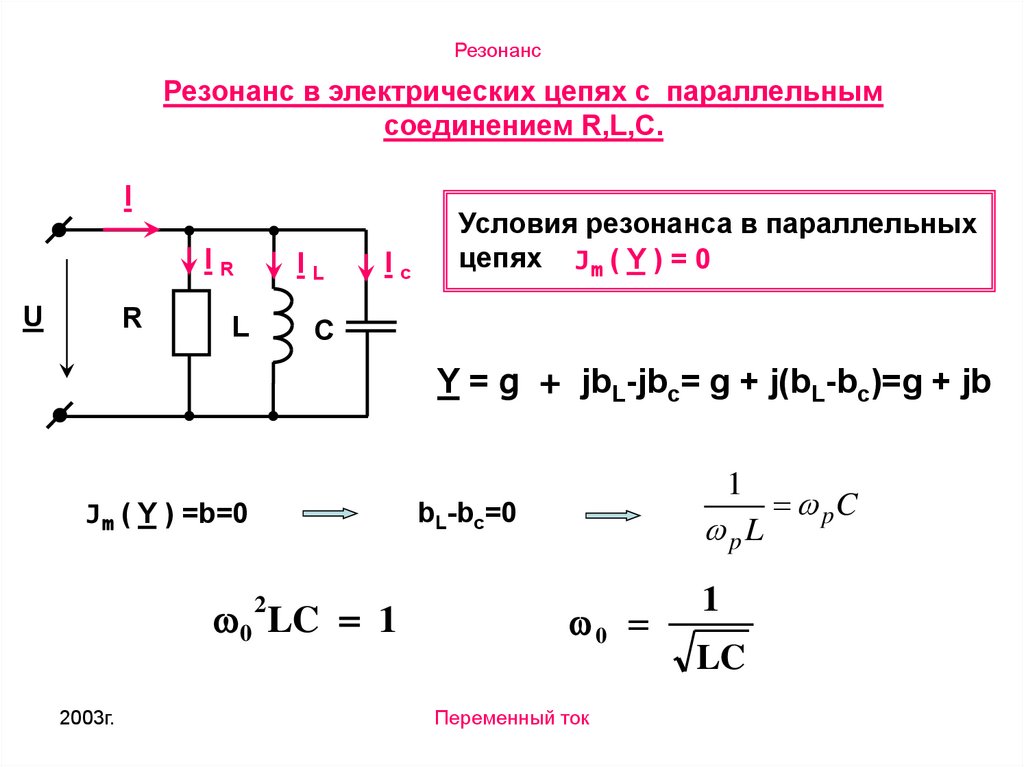
РезонансРезонанс в электрических цепях с параллельным
соединением R,L,C.
I
IR
U
R
IL
Ic
Условия резонанса в параллельных
цепях Jm ( Y ) = 0
С
L
Y = g + jbL-jbc= g + j(bL-bc)=g + jb
1
Jm ( Y ) =b=0
bL-bc=0
0 LC 1
2
2003г.
pL
0
Переменный ток
1
LC
pC
10.
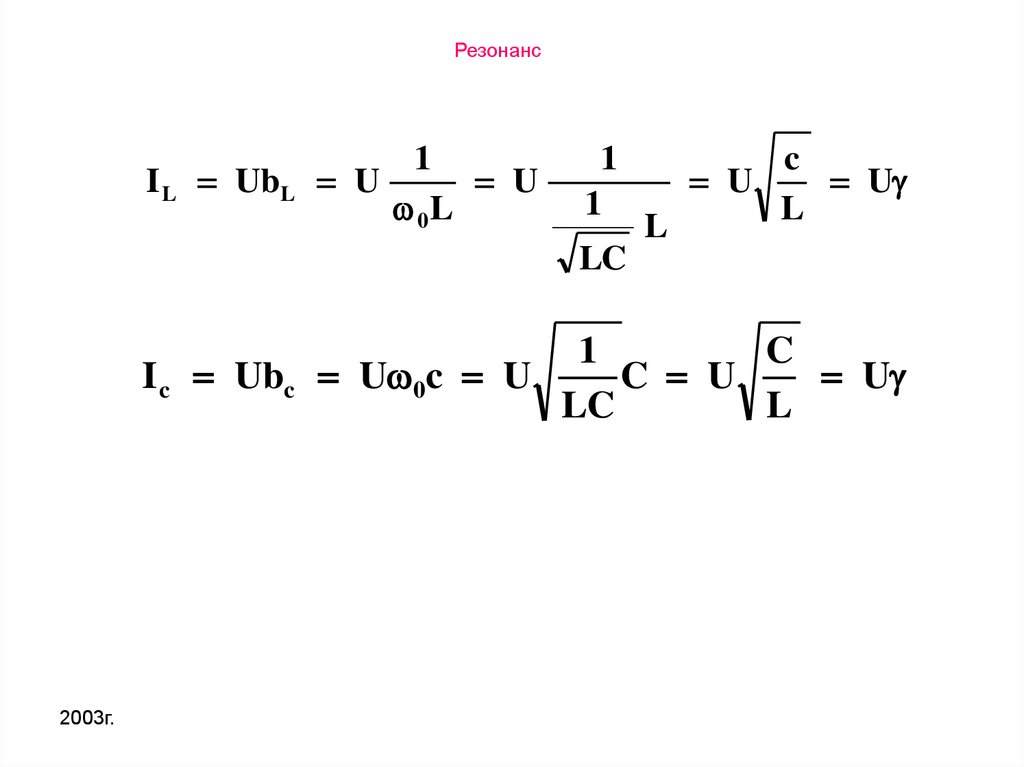
РезонансI L UbL
1
U
U
0 L
1
1
L
c
U
U
L
LC
1
C
I c Ubc U 0c U
C U
U
LC
L
2003г.
11.
РезонансI L UbL U
1
0 L
U
c
1
U
U
1
L
L
LC
1
C
Ic Ubc U 0c U
C U
U
LC
L
2003г.
c
волновая проводимость
L
Переменный ток
12.
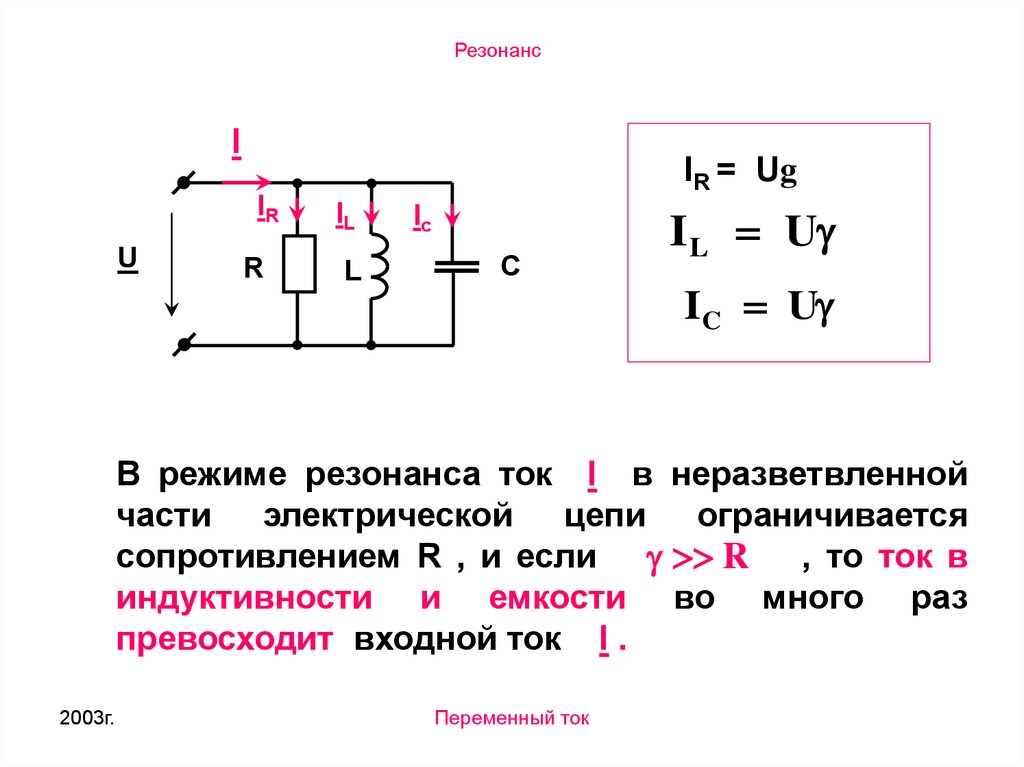
РезонансI
IR = Ug
IR
U
R
IL
L
Ic
С
I L U
IC U
В режиме резонанса ток I в неразветвленной
части электрической цепи ограничивается
сопротивлением R , и если R
, то ток в
индуктивности и емкости во много раз
превосходит входной ток I .
2003г.
Переменный ток
13.
РезонансВекторная диаграмма цепи в режиме резонанаса
токов
I
IR
Ic
I
IL
U
R
IL
Ic
L
U
IR
Токи в индуктивности и емкости равны
полностью компенсируют друг друга.
2003г.
Переменный ток
( IL=Iс ) и
С
14.
РезонансЧастотные характеристики цепи с параллельным
соединением R,L,C
Z,
R,
X
Y(ω)
bL(ω)
φ
g(ω)
ω0
ω0
ω
bc(ω)
bL
1
L
Y
2003г.
π/2
-π/2
bc c
g (b L bc )
2
2
1
g (
c)2
L
Переменный ток
2
ω
15.
РезонансРезонансные кривые параллельного
контура
I
I
I
I'
I'
IR
U
IR(ω)
ω0
2003г.
ω
Переменный ток
R
IL
Ic
L
С
16.
РезонансЗамечания к резонансным режимам электрических цепей.
1.Резонанс напряжений
I
I
R
uR(t)
uL(t)
R
UR
uC(t)
U=0
Рис.2
Рис.1
Если электрическая цепь находится в режиме резонанса
напряжений, то индуктивное сопротивление цепи (или ее
участка) компенсировано емкостным, общее сопротивление
участка равно нулю, и эквивалентно этот участок может быть
представлен закороткой.
2003г.
Переменный ток
17.
Резонанс2. Резонанс токов
I
I'
I
IR
U
IL
R
Ic
L
IR
С
U
Рис.1
R
UR
Рис.2
В режиме резонанса токов , реактивная проводимость участка равна
нулю, т.е. сопротивление участка равно бесконечности. Эквивалентно
этот участок может быть представлен разрывом цепи. Поэтому ток в
неразветвленной части цепи равен нулю.
Указанное относится к "идеальному" резонансу, когда в резонансных
участках
отсутствуют
активные
сопротивления.
Рассмотрим
электрическую цепь Рис 3., с активными сопротивлениями.
2003г.
Переменный ток
18.
РезонансI
I1
I2
L
bLэкв
С
xL
2
R1
U
R1
bcэкв
g1экв
R2
xc
R22 X c2
g2 экв
2
XL
R1
R12 X L2
R2
R22 X c2
Условием резонанса для этой цепи является bLэкв= bcэкв или
xc
R 22 X c2
2003г.
=
xL
R 12 X L2
Переменный ток
19.
РезонансЭквивалентная схема и векторная
диаграмма
I'
I
+J
I1a
U
I2a
g1эк
g2эк
в
в
I1p
I2p
bсэкв
bLэкв
I2
I2p
I2a
I
I1a
I1
Рис.3
I1a=Ug1экв
I1p=UbLэкв
2003г.
I2a=Ug2экв
I2p=Ubcэк
I1p= I2p
I'=0
Переменный ток
I=0
I =I1a + I2a
I1p
+1
20.
РезонансРезонанс в сложных электрических
цепях
Условия фазового резонанса (b=0 или x=0) в разветвленных
электрических цепях дают
уравнения для частоты ω,
которые могут иметь несколько действительных корней. Это
означает, что у разветвленных электрических цепей может
несколько резонансных частот. Кроме того, даже для одной
частоты источника питания различные участки цепи могут
одновременно находится в различных видах резонанса(токов
и напряжений). Резонанс может существовать и в цепях с
магнитосвязанными катушками индуктивности. В этом случае
отрицательная магнитная связь играет роль емкостного
сопротивления, компенсирующего суммарное индуктивное
сопротивление.
2003г.
Переменный ток

















 Физика
Физика








