Похожие презентации:
Числові характеристики випадкових величин, показники варіації; первинна статистична обробка кількісних ознак
1. Числові характеристики випадкових величин, показники варіації; первинна статистична обробка кількісних ознак
1.2.
3.
4.
5.
Генеральна сукупність та вибірка. Репрезентативність вибірки
Параметри генеральної сукупності і вибіркові характеристики
Оцінки генеральних параметрів за вибірковими
характеристиками
Міри положення, міри розсіювання і міри форми при
характеризуванні вибірки
Довірчий інтервал для середнього арифметичного
2. 1. Генеральна сукупність та вибірка. Репрезентативність вибірки
Генеральнасукупність (N) –
сукупність, з якої
обирають певну її
частину для сумісного
дослідження
Вибіркова
сукупність (вибірка)
(n)
Формування вибірки –
повторна і безповторна
вибірки
Репрезенативність вибірки
– формування вибірки, коли
вона найбільш повно
представляє властивості
генеральної сукупності
Метод досягнення –
рандомізація – відбір об’єктів
у вибірку з генеральної
сукупності випадковим чином.
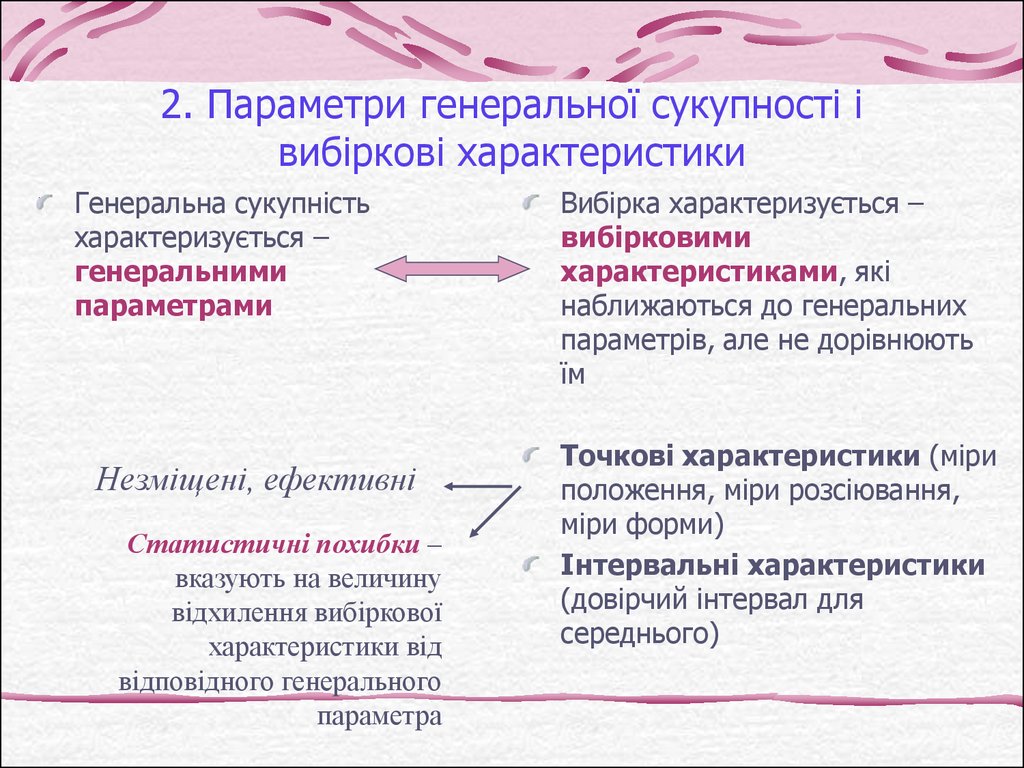
3. 2. Параметри генеральної сукупності і вибіркові характеристики
Генеральна сукупністьхарактеризується –
генеральними
параметрами
Незміщені, ефективні
Статистичні похибки –
вказують на величину
відхилення вибіркової
характеристики від
відповідного генерального
параметра
Вибірка характеризується –
вибірковими
характеристиками, які
наближаються до генеральних
параметрів, але не дорівнюють
їм
Точкові характеристики (міри
положення, міри розсіювання,
міри форми)
Інтервальні характеристики
(довірчий інтервал для
середнього)
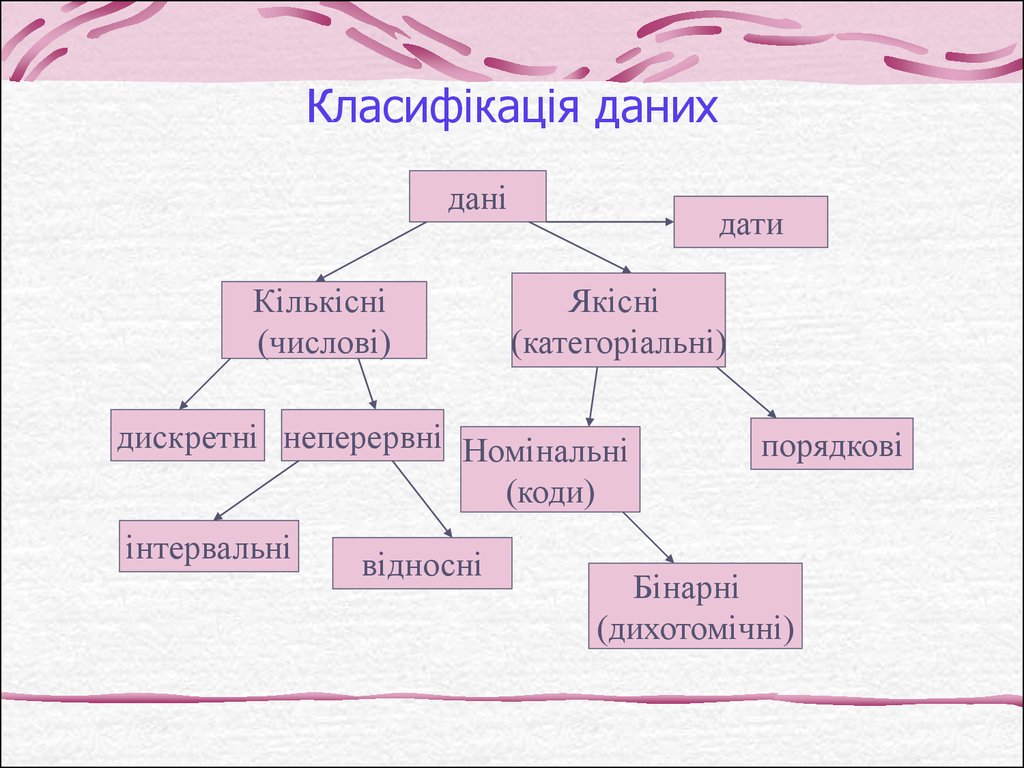
4. Класифікація даних
даніКількісні
(числові)
дати
Якісні
(категоріальні)
дискретні неперервні Номінальні
(коди)
інтервальні
відносні
порядкові
Бінарні
(дихотомічні)
5. Попереднє впорядкування даних
Ранжування –розміщення всіх значень
ознаки хі в порядку
зростання (спадання)
Ряд розподілу – ряд
ранжованих даних, в якому
розмах варіації (хmin – xmax)
розбивають на рівні
інтервали (класи) і
шукають частоту
зустрічаємості значень в
кожному класі
Гістограма –
графік розподілу
частот
частота
Значення ознаки
(класові інтервали)
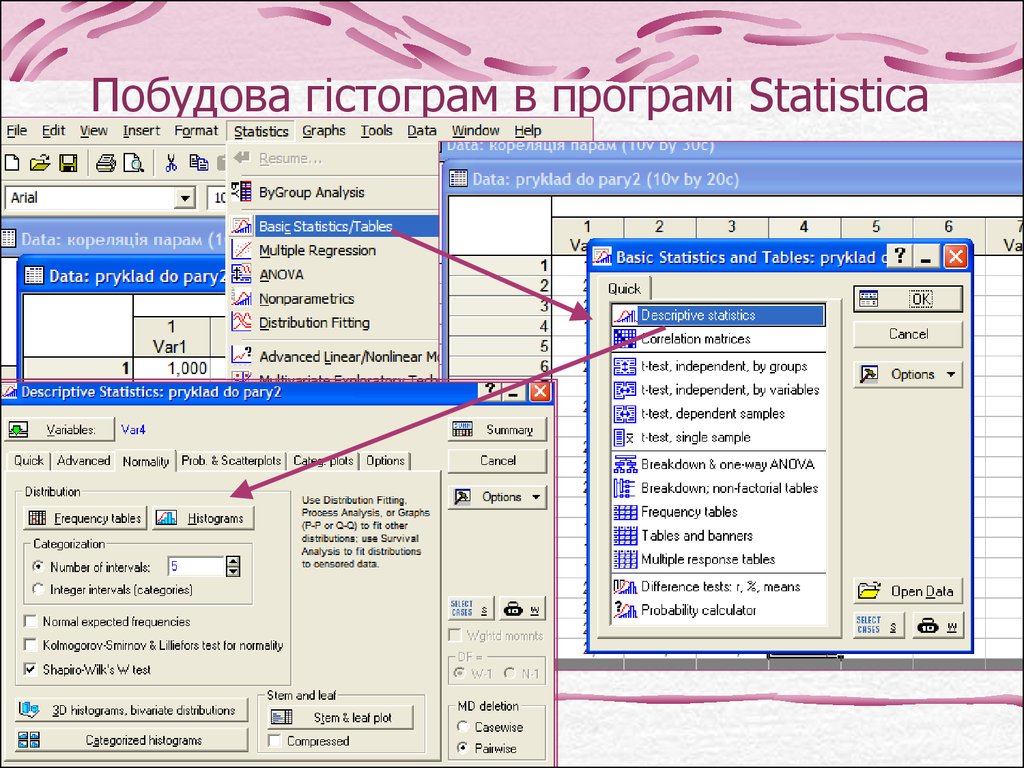
6. Побудова гістограм в програмі Statistica
7. Розбиття вибірок на класи
ПравилоСтарджеса:
Число класів – k:
k = 1 + 3.31*lg (n)
n
10-20
30-50
60-90
100200
300400
500800
9001500
2000
k
4
5-6
7
8
9
10
11
12
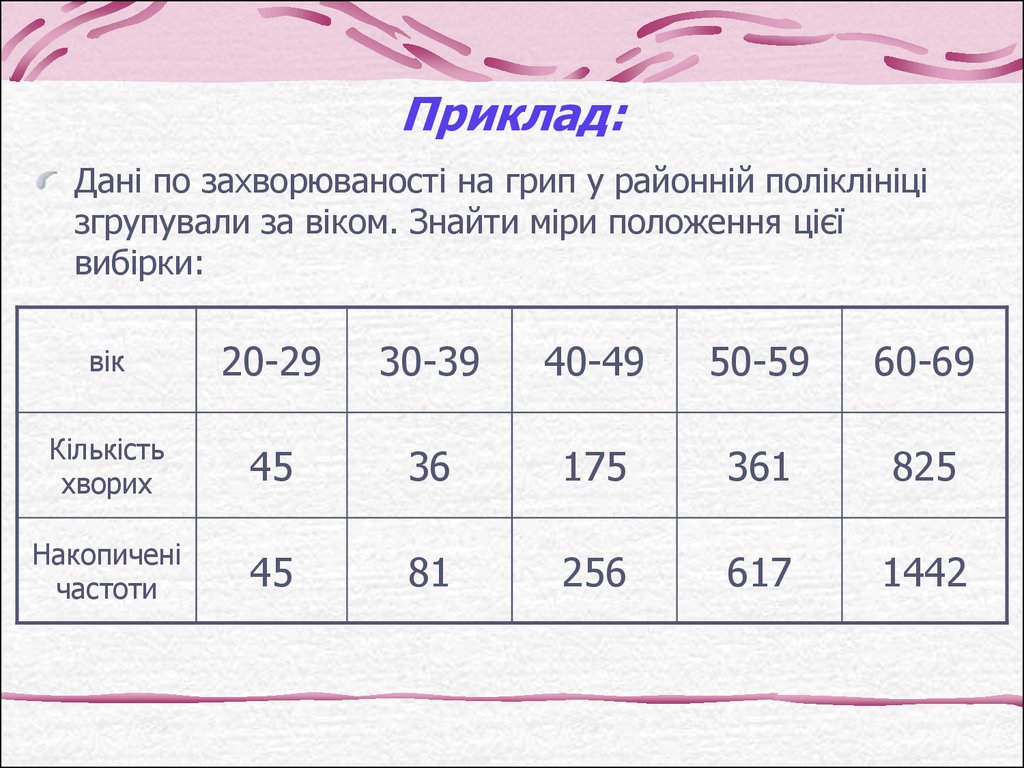
8. Приклад:
Дані по захворюваності на грип у районній поліклініцізгрупували за віком. Знайти міри положення цієї
вибірки:
вік
20-29
30-39
40-49
50-59
60-69
Кількість
хворих
45
36
175
361
825
Накопичені
частоти
45
81
256
617
1442
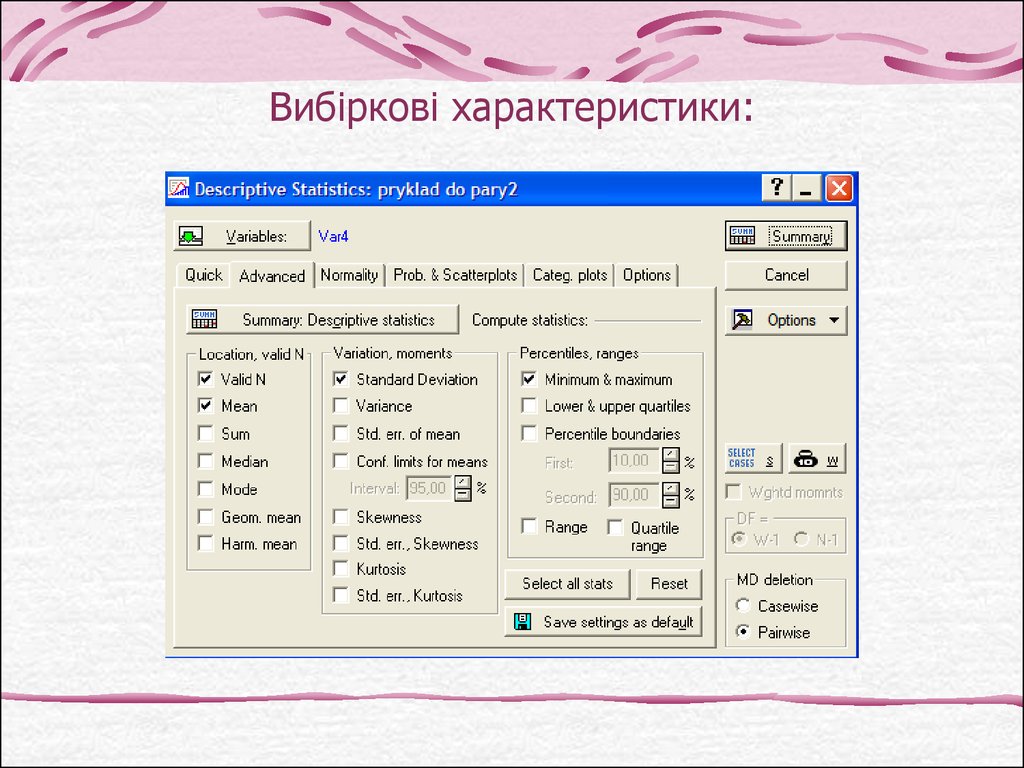
9. Вибіркові характеристики:
10. 3. Міри положення Середнє арифметичне (mean)
kn
x
x x n
i 1
n
i
j 1
k
j
n
j 1
j
x [24.5 * 45 34.5 * 36
j
Xi - значення (точка) вибірки,
n – загальний об’єм вибірки
Хj – значення вибірки коли воно
зустрічається декілька разів
(серединне значення інтервалу),
nj – частота, з якою
спостерігається значення хj
(об’єм інтервалу)
k – кількість інтервалів
44.5 *175 54.5 * 361
64.5 * 825] / 1442 58.57
11. Медіана (median)
Me xMem
h(
2
x
mxmax )
mm
mx – середина вибірки (1/2
вибірки)
h – ширина інтервалу,
mm – об’єм медіанного
інтервалу,
хМе – початок медіанного
інтервалу,
mxmax – частота, накопичена
на початок медіанного
класу
- це значення, яке ділить
ранжований варіаційний ряд на
2 рівні за об’ємом групи
10 * 721 617
Me 60
61.26
825
12. Мода (mode)
h mMo mMo 1M o xMo
2mMo mMo 1 mMo 1
xMo – початок модального
інтервалу,
h – ширина інтервалу,
mMo – об’єм модального
інтервалу,
mMo-1 – об’єм інтервалу перед
модальним
mMo+1 – об’єм інтервалу після
модального
- це значення, яке
спостерігається
найбільшу кількість
разів
10 * (825 361)
Mo 60
65
2 * 825 361 0
13. Міри розсіяння (варіації) - показують розкид даних у вибірці відносно середнього значення
Варіаційний розмах (розмах, range)Rv xmax xmin
Rv 69 20 49
Емпірична дисперсія (вибіркова
дисперсія) (variance)
N
D s2
2
(
x
x
)
i
i 1
N 1
[( 24.5 58.57) 2 (34.5 58.57) 2 (44.5 58.57) 2 (54.5 58.57) 2 (64.5 58.57) 2 ]
D
1442 1
1.38
14. Стандартне відхилення (середнє квадратичне відхилення) (standard deviation)
1.38 1.175s D
Інтерквартильний розмах (quartile
range)
Q3 Q1
Xmin
Q1
0%
25%
Q2
Q3
Xmax
75% 100%
50%
Me
Q1 – нижня квартиль (lower quartile)
Q3 – верхня квартиль (upper quartile)
Перцентіль – значення, яке міститься на межі певного %
ранжованої вибірки
15. Міри форми
Асиметрія (skewness) – вказує, наскільки розподілсиметричний відносно середнього (позитивна і
негативна асиметрія)
n
xi x
*
(n 1)( n 2) i 1
n
3
Ексцес (kurtosis) – міра гостроверхості відносно
нормального розподілу (позитивний і негативний)
n(n 1)
3(n 1) 2
xi x
*
(n 1)( n 2)( n 3) i 1 (n 2)( n 3)
n
4
16. Довірчий інтервал для генерального середнього
Довірчий інтервал – інтервал, відносно якого з початковозаданою ймовірністю Р (Р=1-α) можна стверджувати, що він містить
невідоме значення генерального параметра
Р – довірча ймовірність,
P = 0.95
t1 = 1.96
α – рівень значущості
P = 0.99 (95%
t2 = 2.58
Довірчий інтервал для генерального середнього
confidence limits of mean):
P = 0.999 t3 = 3.29
x t
58.57 1.96
n
M ( x) x t
n
1.175
1.175
M ( x) 58.57 1.96
37.97
37.97
58.5 M ( x) 58.64
t – табличне значення
розподілу Стьюдента з
числом ступенів свободи k
і довірчою ймовірністю Р











 Математика
Математика








