Похожие презентации:
Производная
1.
y f (x) уx0
f/(x)
f(x)
2
х
1
2.
Тема3.
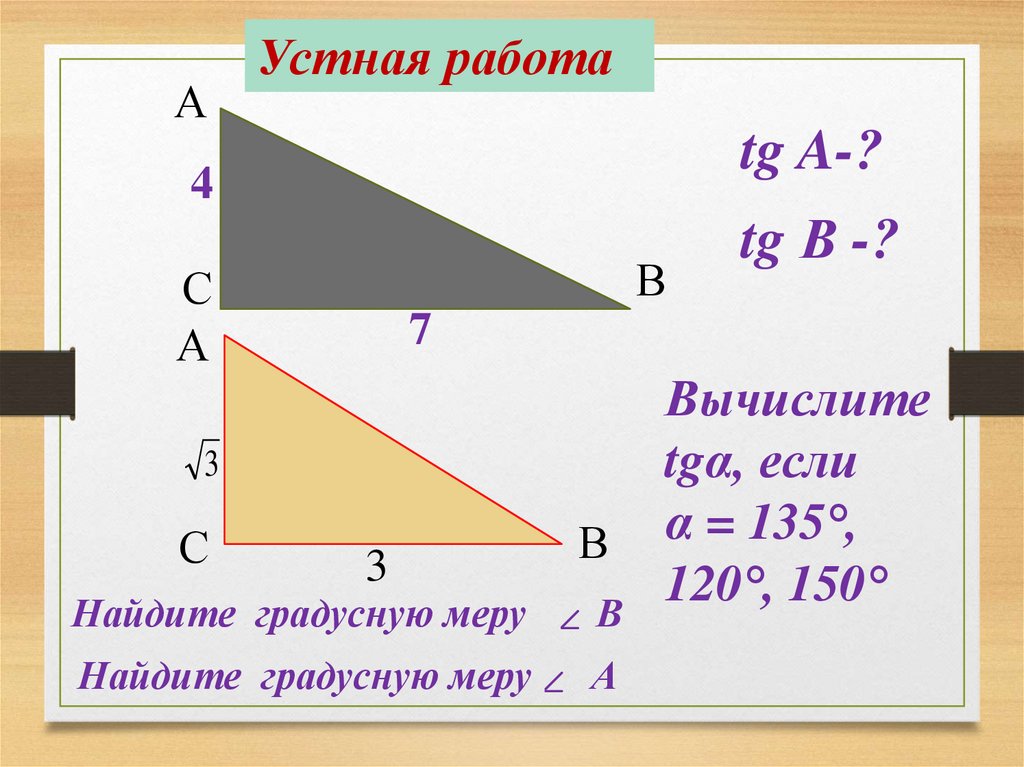
АУстная работа
tg A-?
4
В
С
А
7
3
С
tg В -?
3
В
Найдите градусную меру
В
Найдите градусную меру
А
Вычислите
tgα, если
α = 135°,
120°, 150°
4.
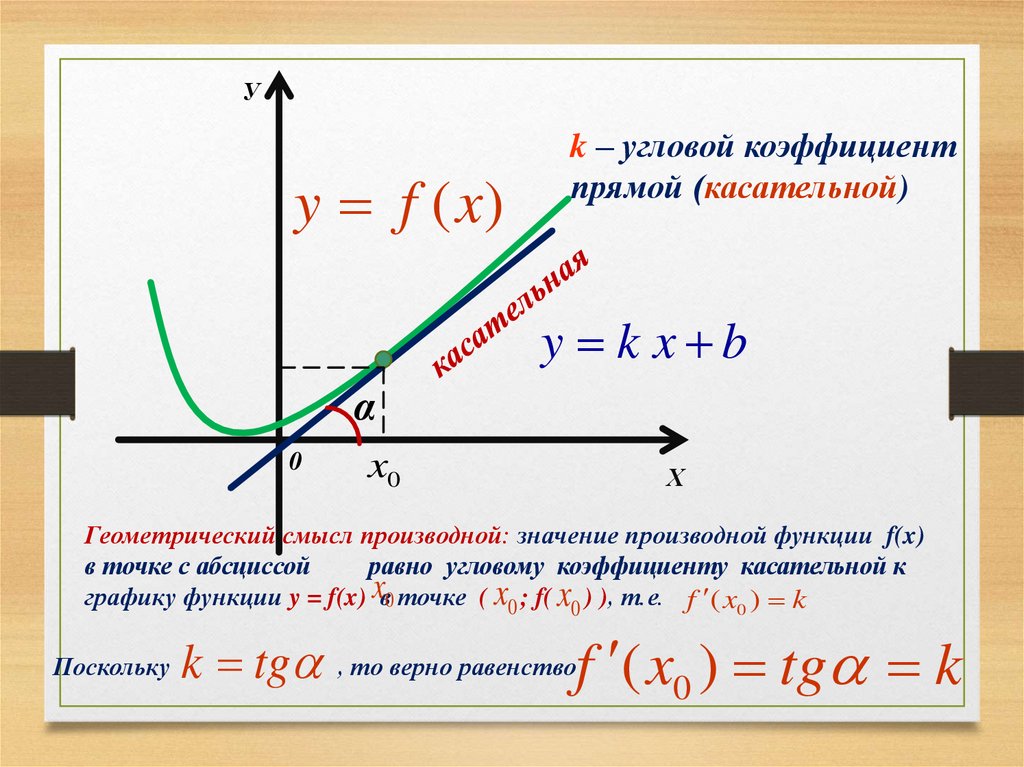
Уy f (x)
k – угловой коэффициент
прямой (касательной)
y k x b
α
0
x0
Х
Геометрический смысл производной: значение производной функции f(x)
в точке с абсциссой
равно угловому коэффициенту касательной к
графику функции y = f(x) xв0 точке ( x0 ; f( x0 ) ), т.е. f ( x0 ) k
Поскольку
k tg
f ( x0 ) tg k
, то верно равенство
5.
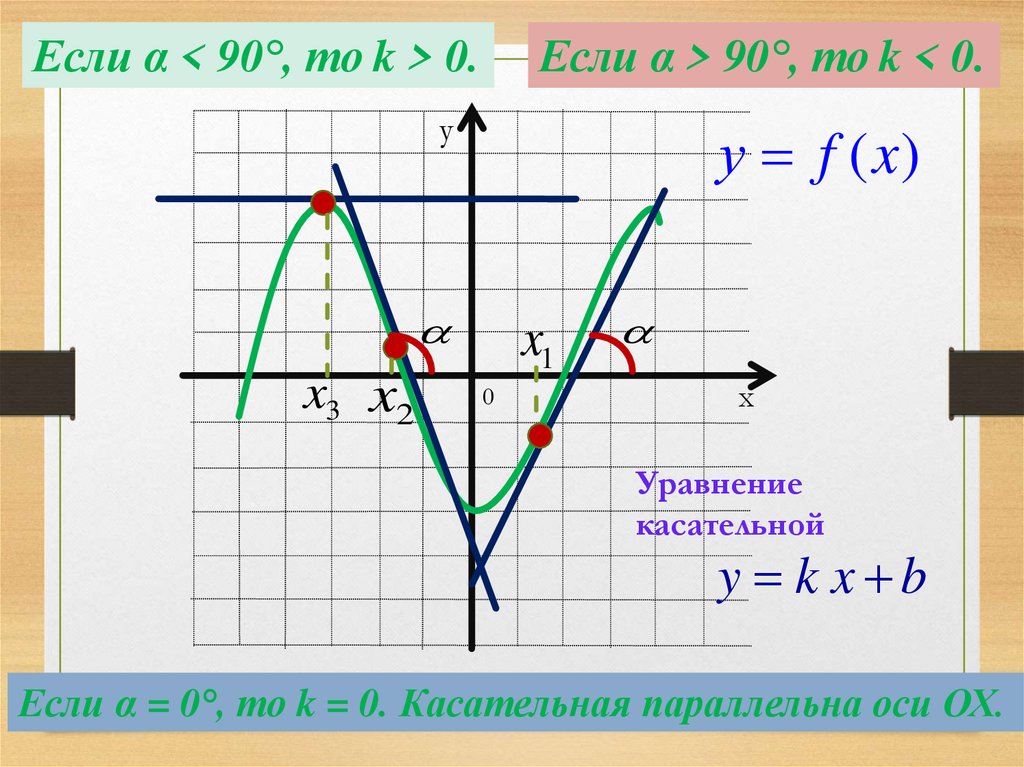
Если α < 90°, то k > 0.Если α > 90°, то k < 0.
у
у f (x)
x3 x2
x1
0
х
Уравнение
касательной
y k x b
Если α = 0°, то k = 0. Касательная параллельна оси ОХ.
6.
Острый или тупой угол образуеткасательная к графику функции в точке х₀
с положительной полуосью Ох?
y 2 x , x0 1
2
y ( x 5) , x0 3
3
2
y x x , x0 1
2
Чему равен тангенс угла наклона
касательной к графику функции y = x² + 2
в точке х₀ = -1?
7.
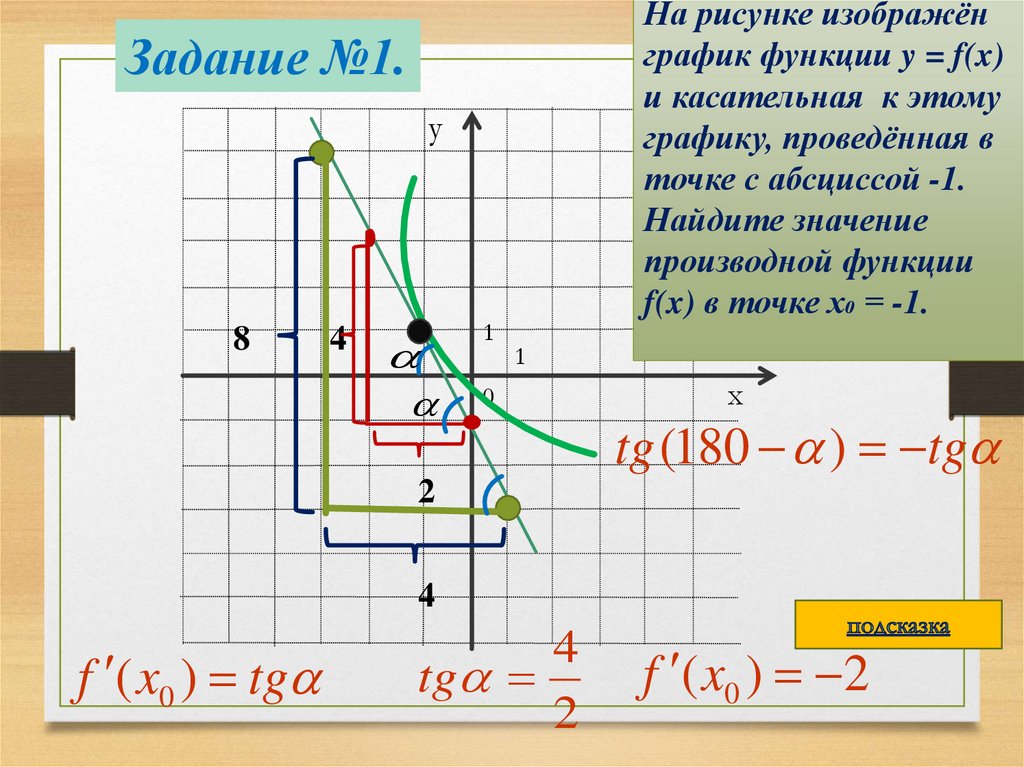
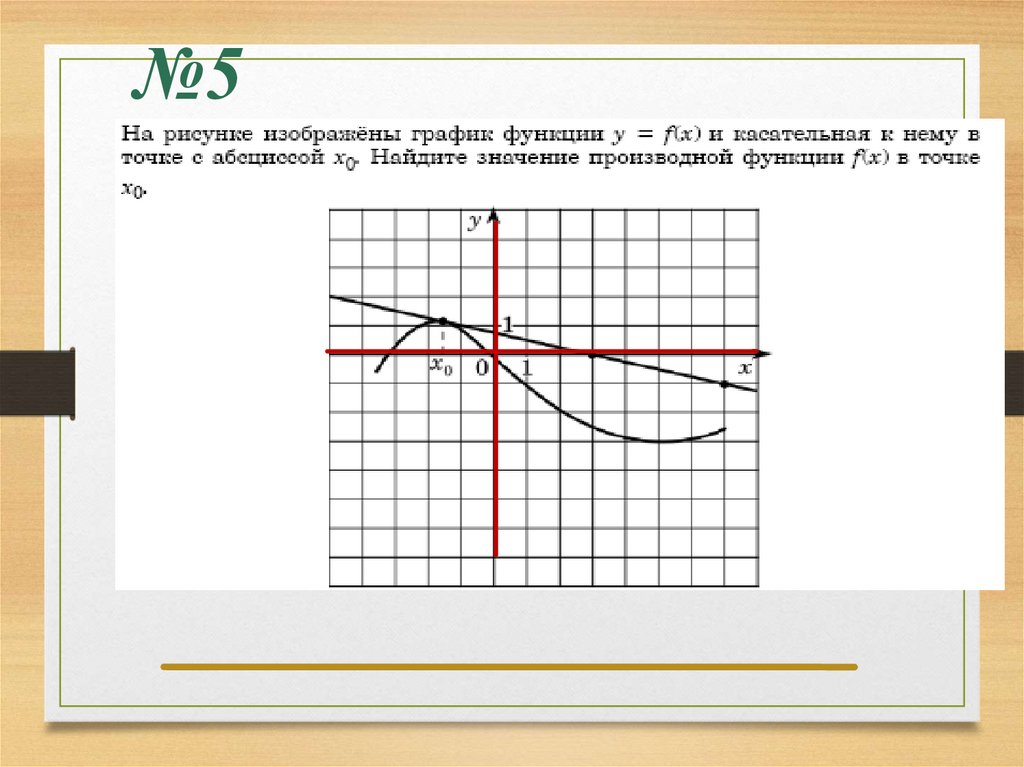
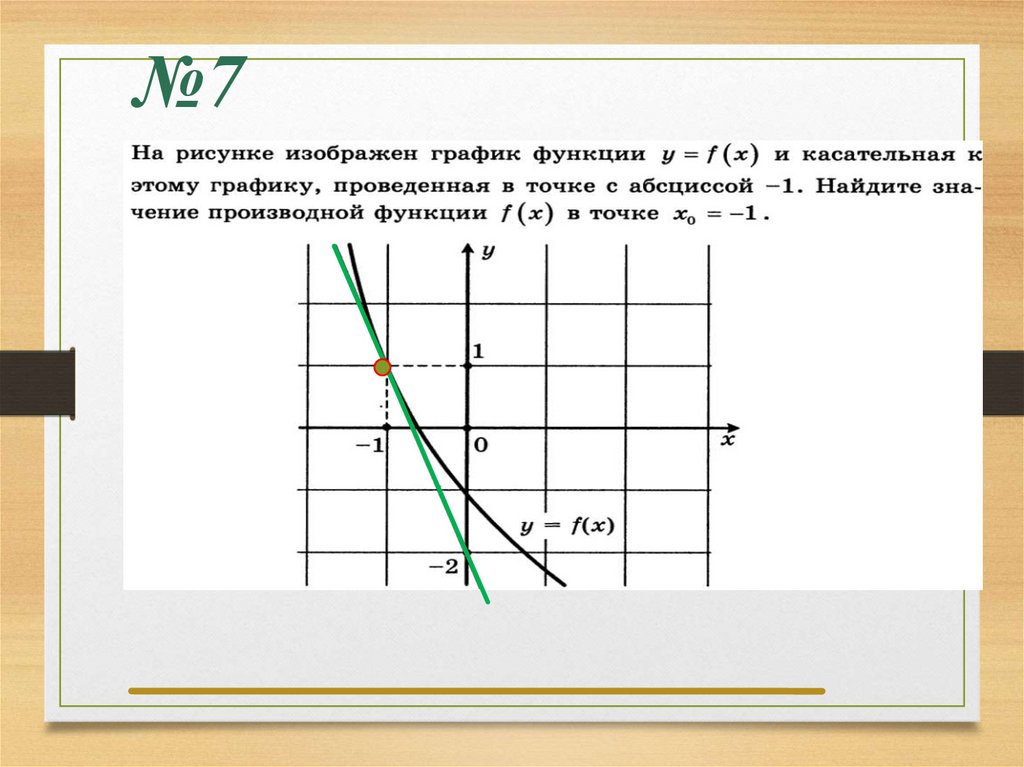
На рисунке изображёнграфик функции y = f(x)
и касательная к этому
графику, проведённая в
точке с абсциссой -1.
Найдите значение
производной функции
f(x) в точке х₀ = -1.
Задание №1.
у
8
4
1
1
0
х
tg (180 ) tg
2
4
f ( x0 ) tg
4
tg
2
f ( x0 ) 2
8.
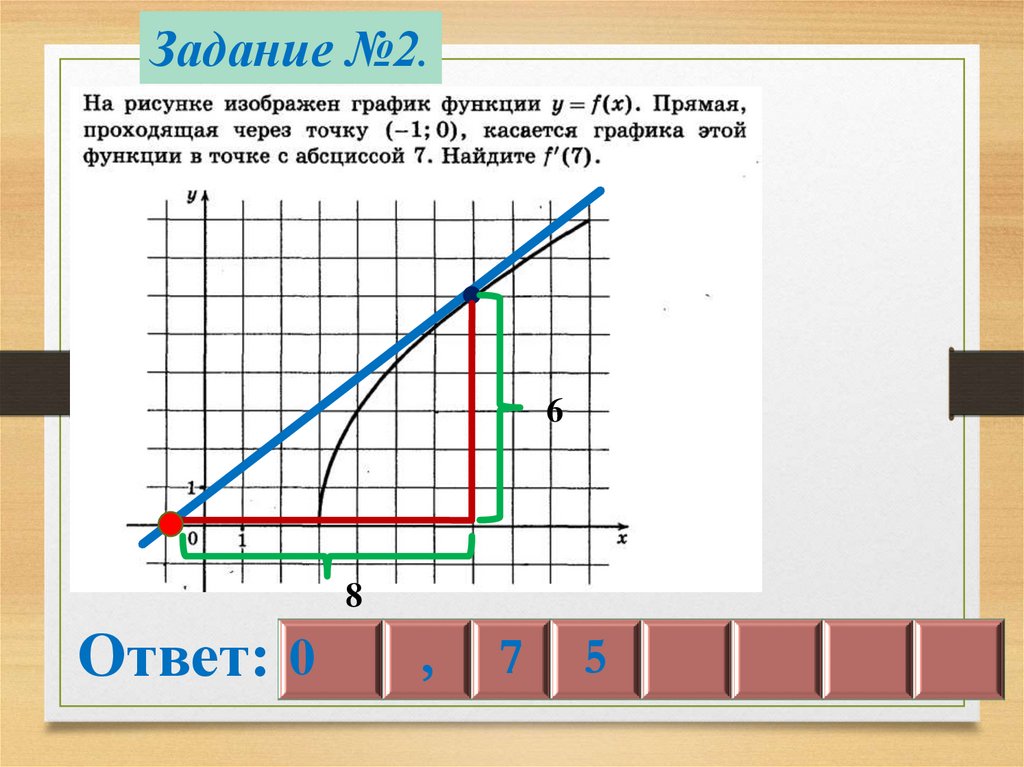
Задание №2.6
8
Ответ: 0
,
7
5
9.
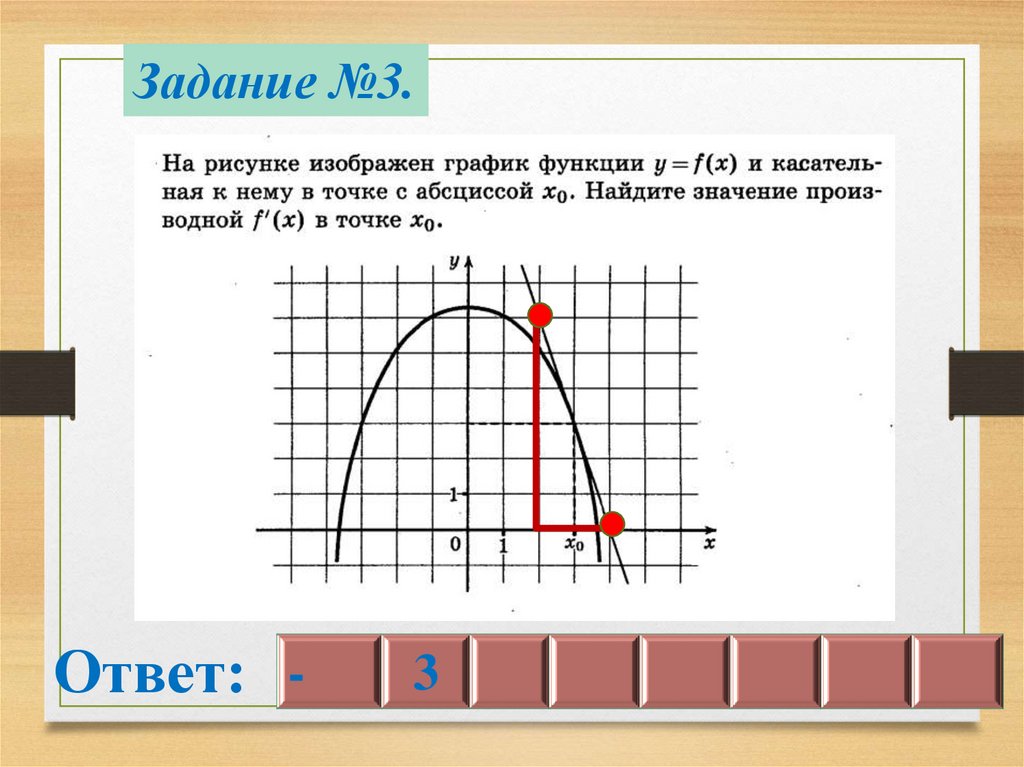
Задание №3.Ответ: -
3
10.
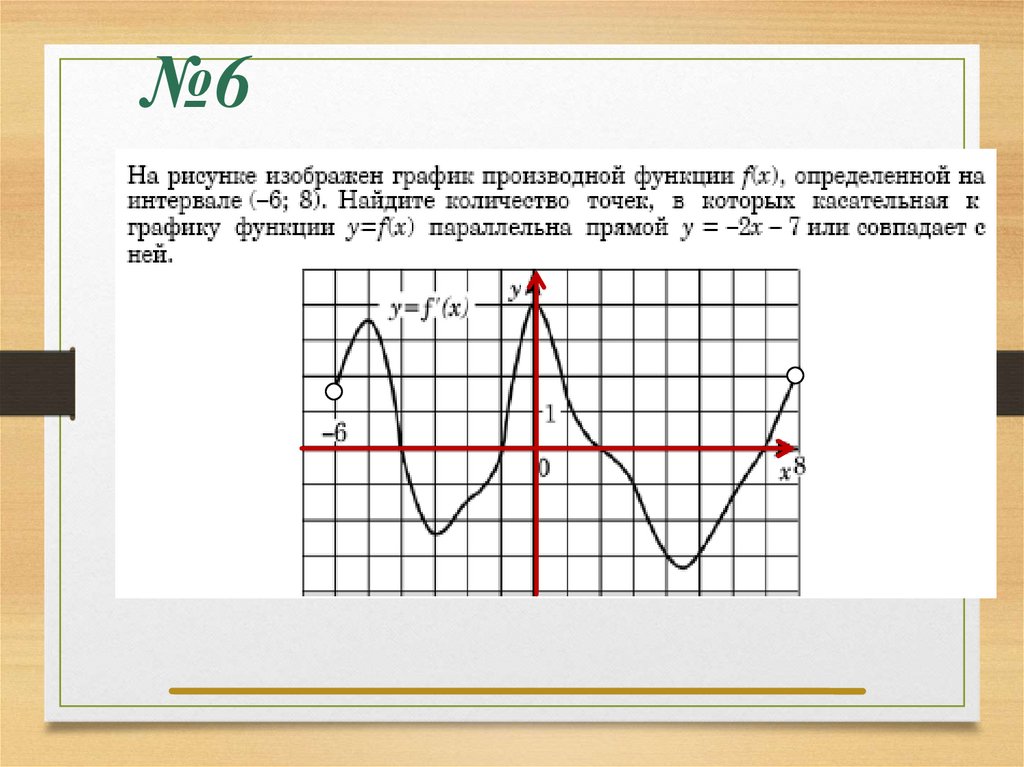
Задание №4.На рисунке изображён график производной функции y = f (x),
определённой на интервале (-5;6). Найдите количество
точек, в которых касательная к графику функции y = f(x)
параллельна прямой у = 2х – 5 или совпадает с ней.
у f (x)
у
2
0
f ( x) 2
Ответ: 4
х
11.
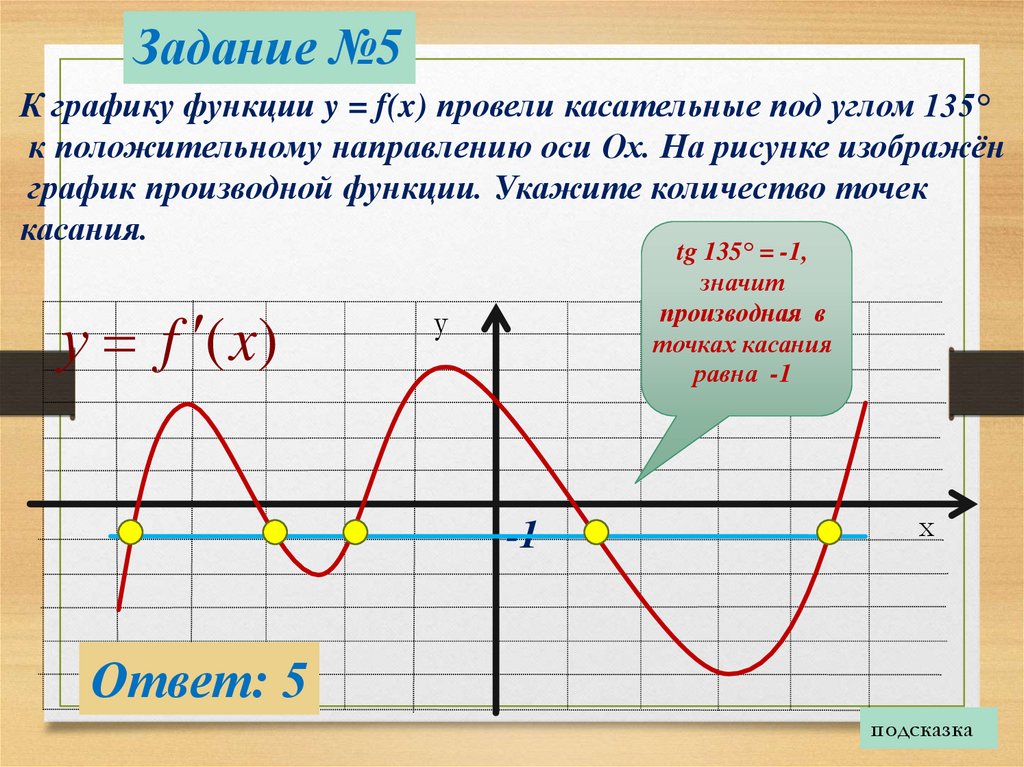
Задание №5К графику функции y = f(x) провели касательные под углом 135°
к положительному направлению оси Ох. На рисунке изображён
график производной функции. Укажите количество точек
касания.
у f (x)
tg 135° = -1,
значит
производная в
точках касания
равна -1
у
-1
х
Ответ: 5
подсказка
12.
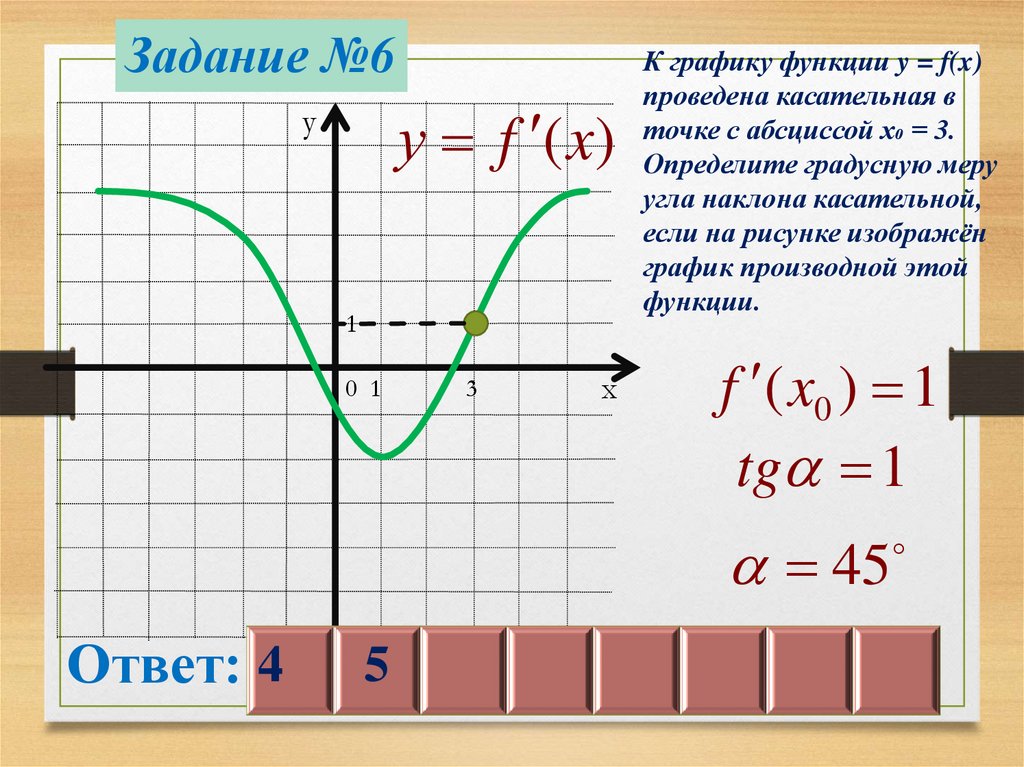
Задание №6у f (x)
у
1
0 1
3
х
К графику функции y = f(x)
проведена касательная в
точке с абсциссой х₀ = 3.
Определите градусную меру
угла наклона касательной,
если на рисунке изображён
график производной этой
функции.
f ( x0 ) 1
tg 1
45
Ответ: 4
5
13.
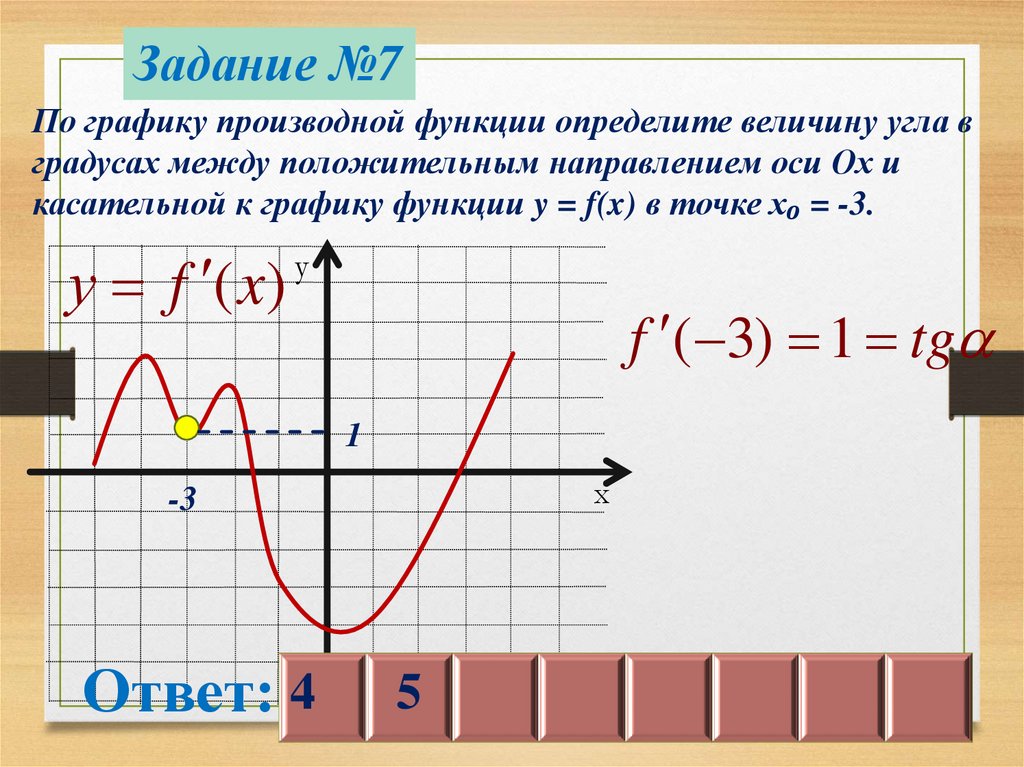
Задание №7По графику производной функции определите величину угла в
градусах между положительным направлением оси Ох и
касательной к графику функции y = f(x) в точке х₀ = -3.
у f (x)
у
f ( 3) 1 tg
1
х
-3
Ответ: 4
5
14.
Задание №8Ответ: 0
,
Задание №9
Ответ:
-
1
5
15.
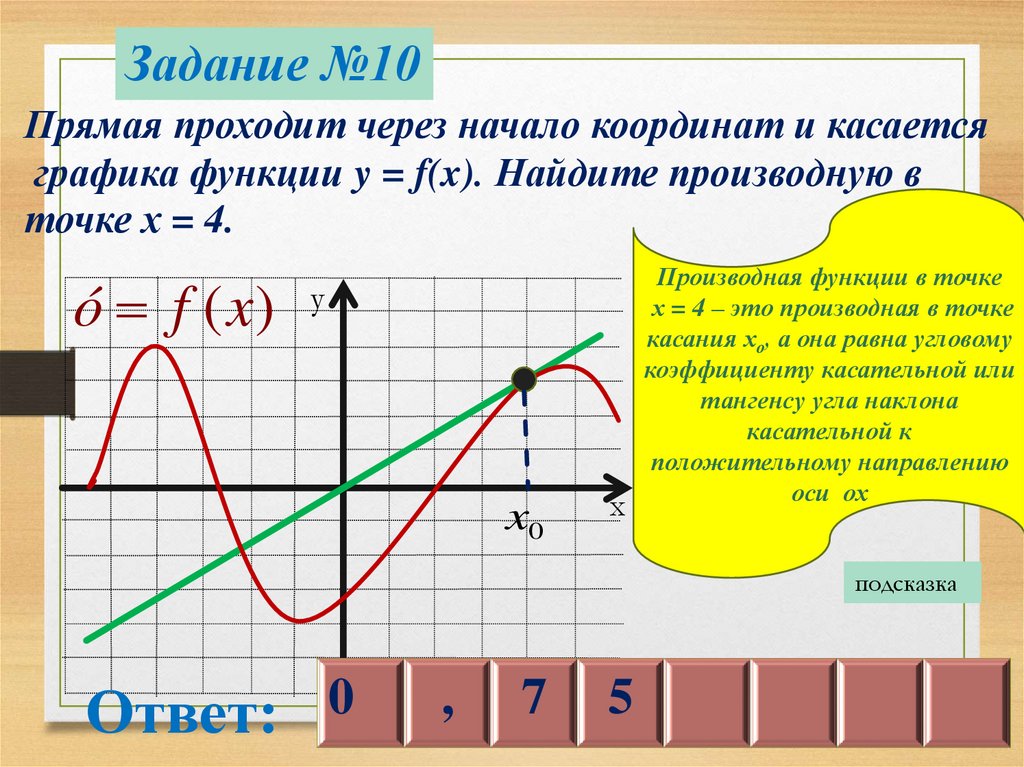
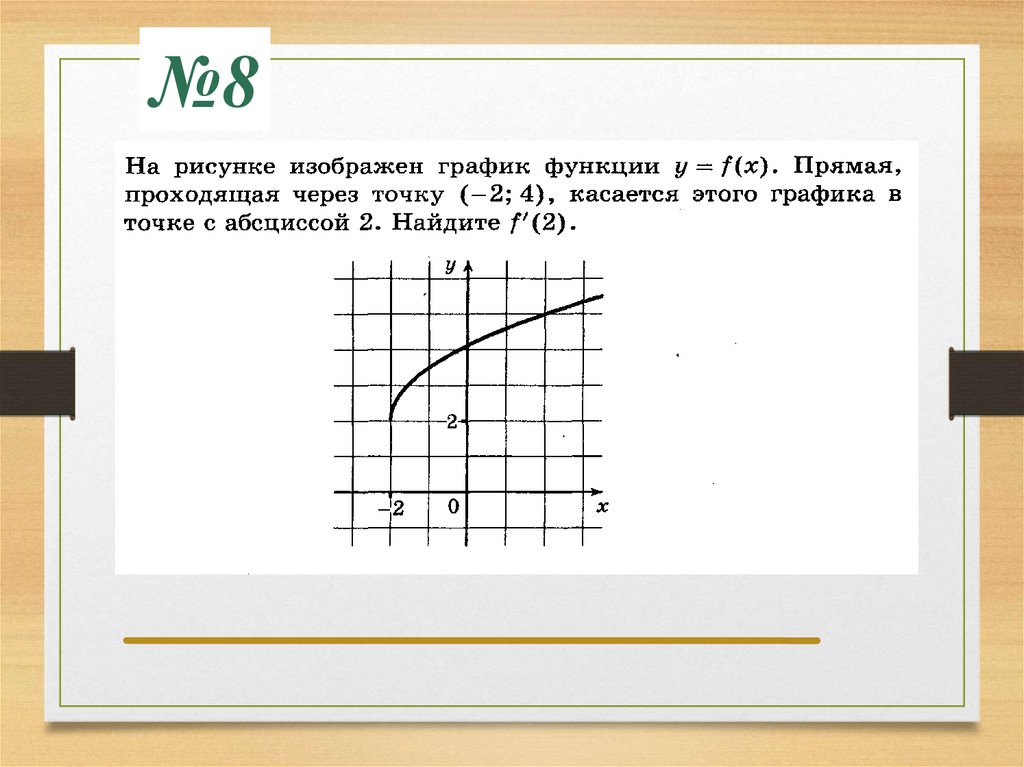
Задание №10Прямая проходит через начало координат и касается
графика функции y = f(x). Найдите производную в
точке х = 4.
ó f (x)
у
x0
х
Производная функции в точке
х = 4 – это производная в точке
касания хо, а она равна угловому
коэффициенту касательной или
тангенсу угла наклона
касательной к
положительному направлению
оси ох
подсказка
Ответ: 0
,
7
5
16.
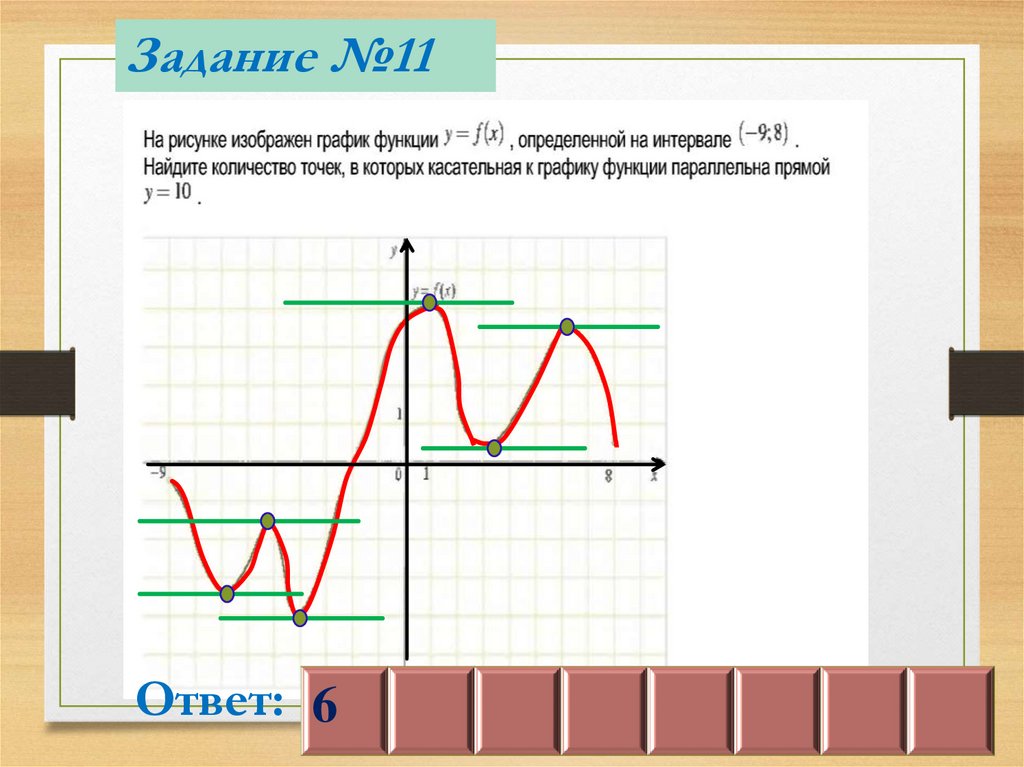
Задание №11Ответ: 6
17.
18.
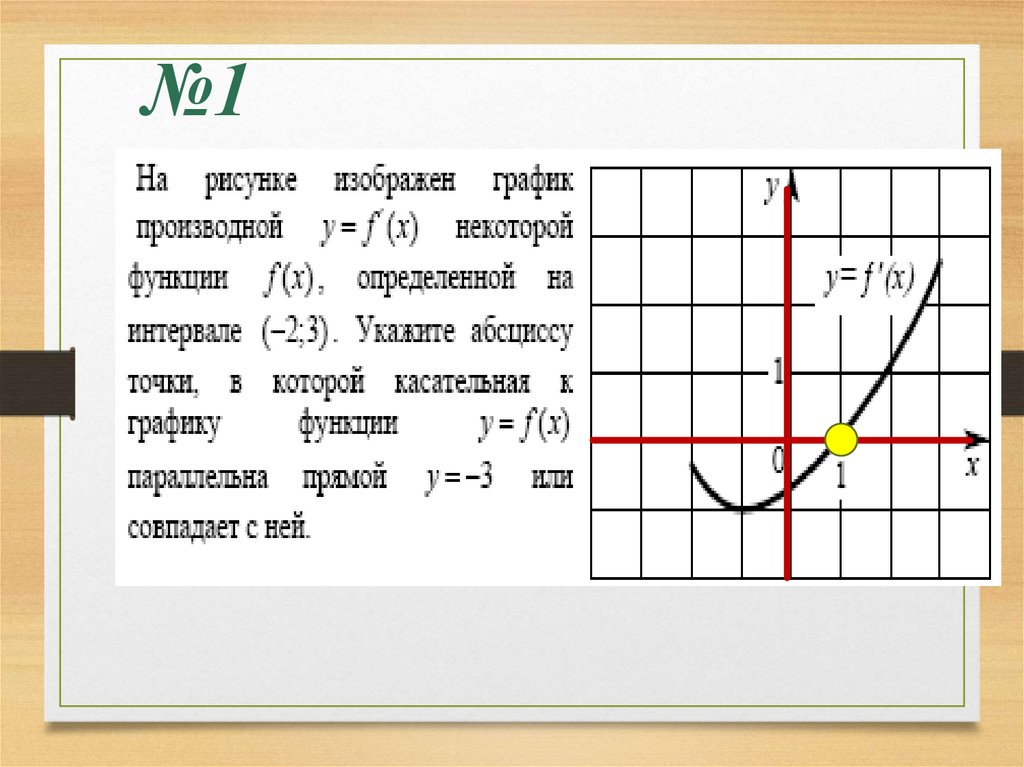
№119.
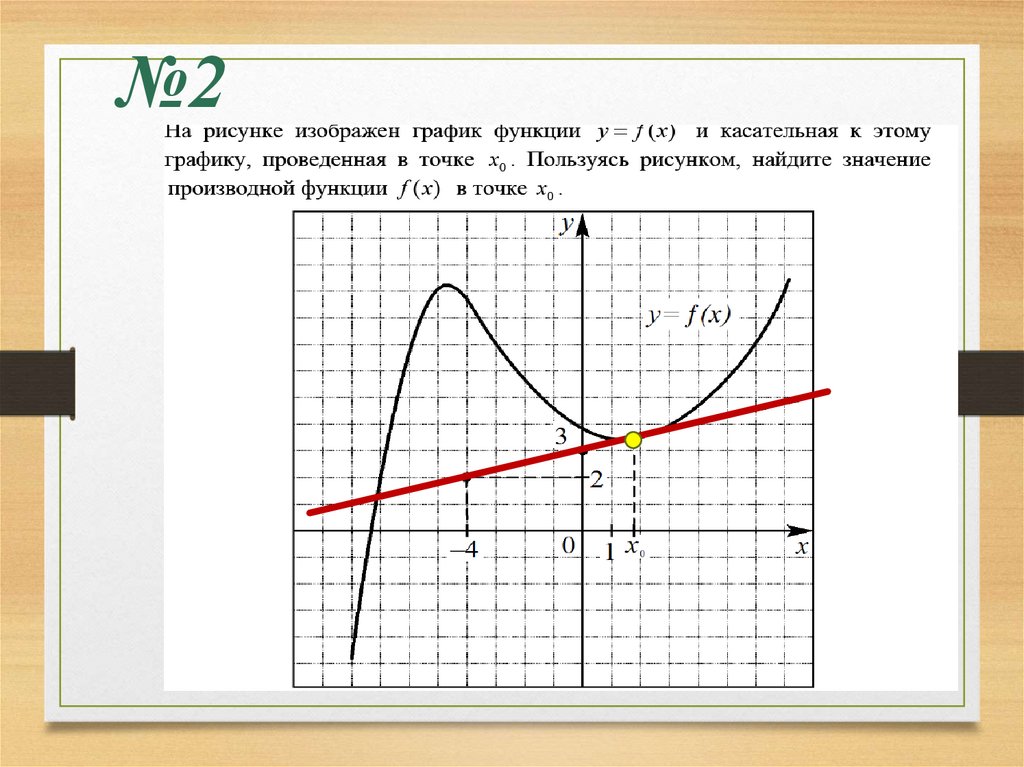
№220.
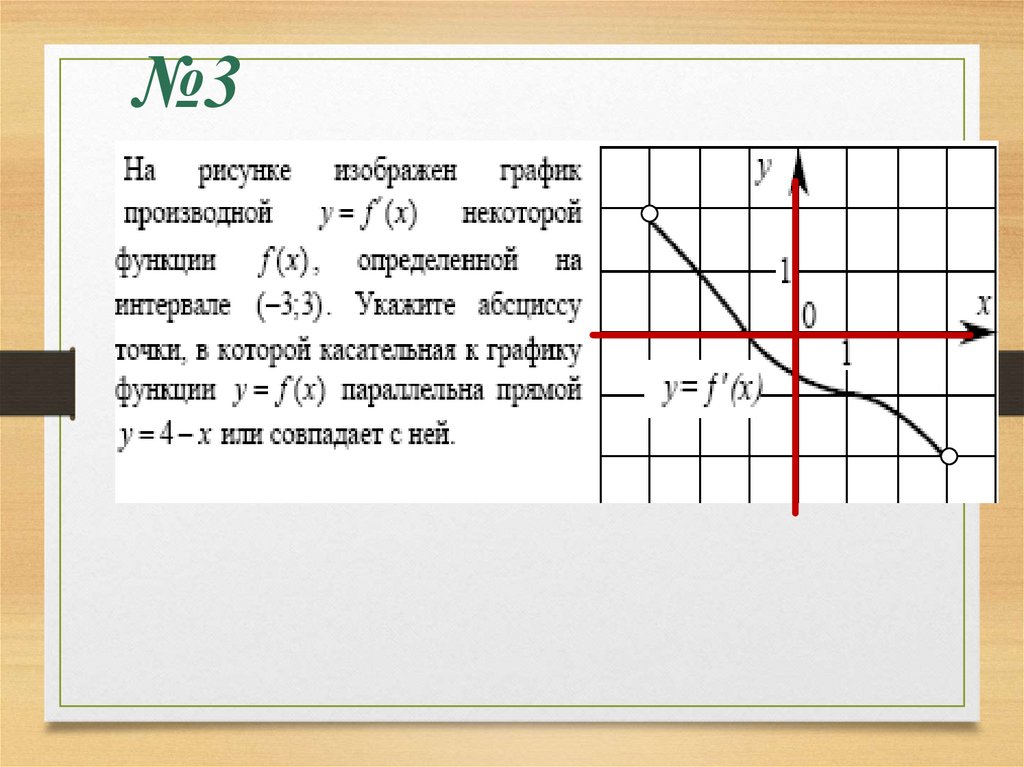
№321.
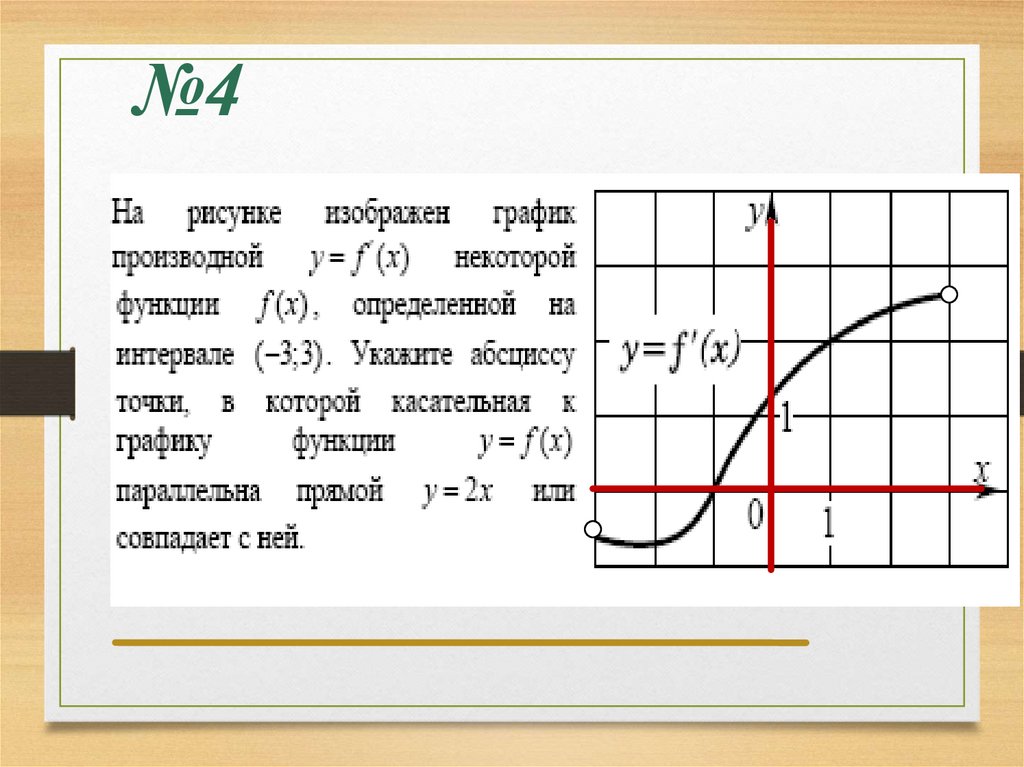
№422.
№523.
№624.
№725.
№826.
Проверьте себя№1
1
№5
- 0, 25
№2
0, 25
№6
4
№3
1
№7
- 3
№4
1
№8
0, 25
27.
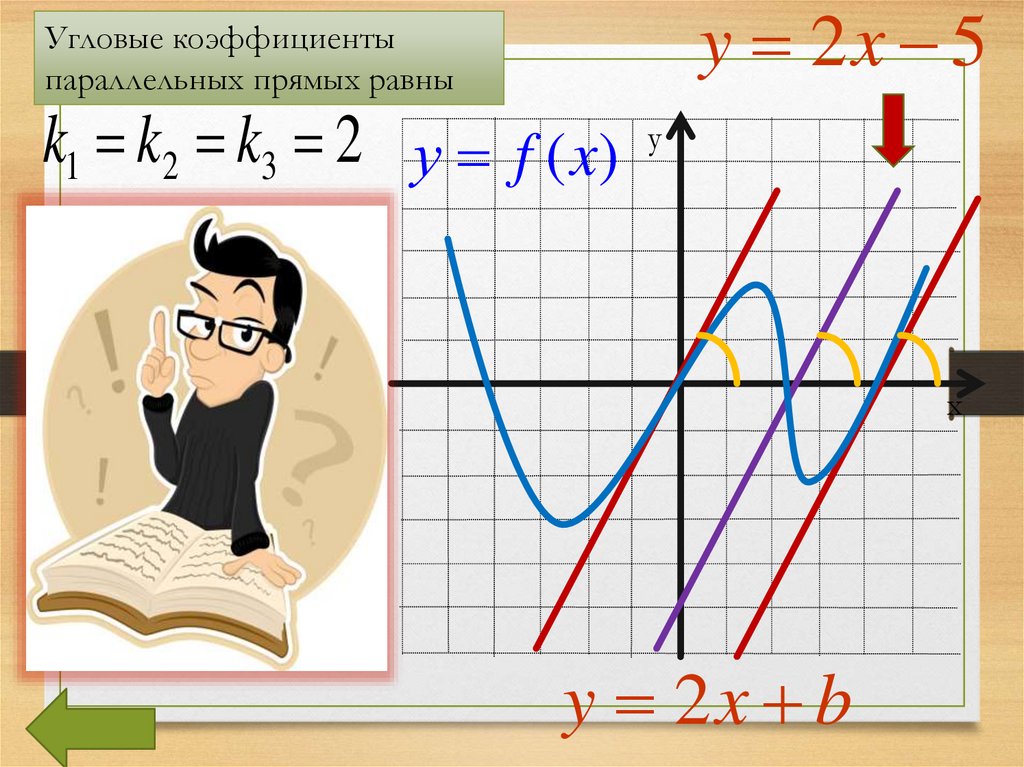
y 2x 5Угловые коэффициенты
параллельных прямых равны
k1 k2 k3 2 у f (x)
у
х
y 2x b
28.
f ( x0 ) tg kДля вычисления углового
коэффициента касательной
достаточно найти отрезок
касательной с концами в вершинах
клеток и, считая его гипотенузой
прямоугольного треугольника, найти
отношение катетов.
29.
• Так как касательная параллельна прямой y=8x+11, тоих угловые коэффициенты совпадают, т.е. угловой
коэффициент касательной равен восьми
f ( x0 ) tg k
xo – абсцисса искомой точки касания
k = 8.
30.
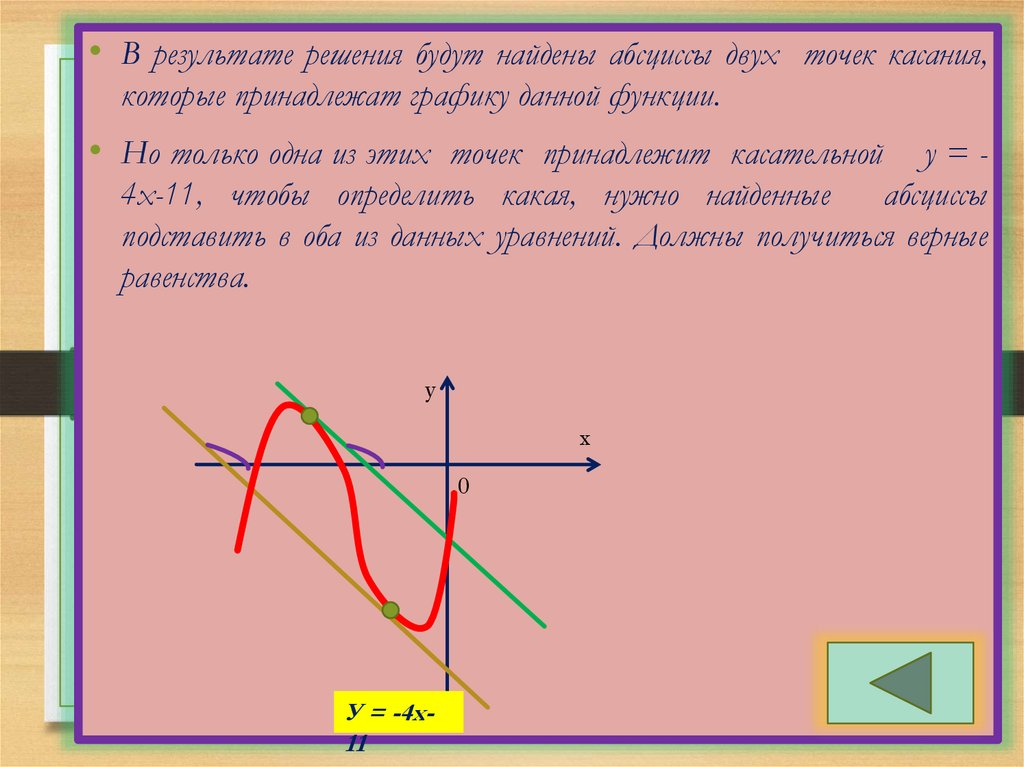
• В результате решения будут найдены абсциссы двух точек касания,которые принадлежат графику данной функции.
• Но только одна из этих точек принадлежит касательной
у=4х-11, чтобы определить какая, нужно найденные
абсциссы
подставить в оба из данных уравнений. Должны получиться верные
равенства.
у
х
0
У = -4х11
31.
• Чтобы найти угловой коэффициент касательной к графику функции взаданной точке или значение производной функции в точке, надо найти
тангенс угла наклона касательной к положительному направлению оси Ох.
Для этого достаточно найти отрезок касательной с концами в вершинах
клеток и, считая его гипотенузой прямоугольного треугольника, найти
отношение противолежащего катета к прилежащему.
• Если на рисунке нет касательной, но известны точки, через которые она
проходит, сначала надо провести касательную, а потом рассмотреть
прямоугольный треугольник, в котором найти отношение катетов.
• Если угол наклона касательной к положительному направлению оси Ох
острый, то угловой коэффициент касательной
функции в точке положительны.
и значение производной
• Если угол наклона касательной к положительному направлению оси Ох
тупой, то угловой коэффициент касательной
функции в точке отрицательны.
и значение производной











 Математика
Математика








