Похожие презентации:
Векторы. Основные понятия
1. В е к т о р ы. О с н о в н ы е п о н я т и я.
2.
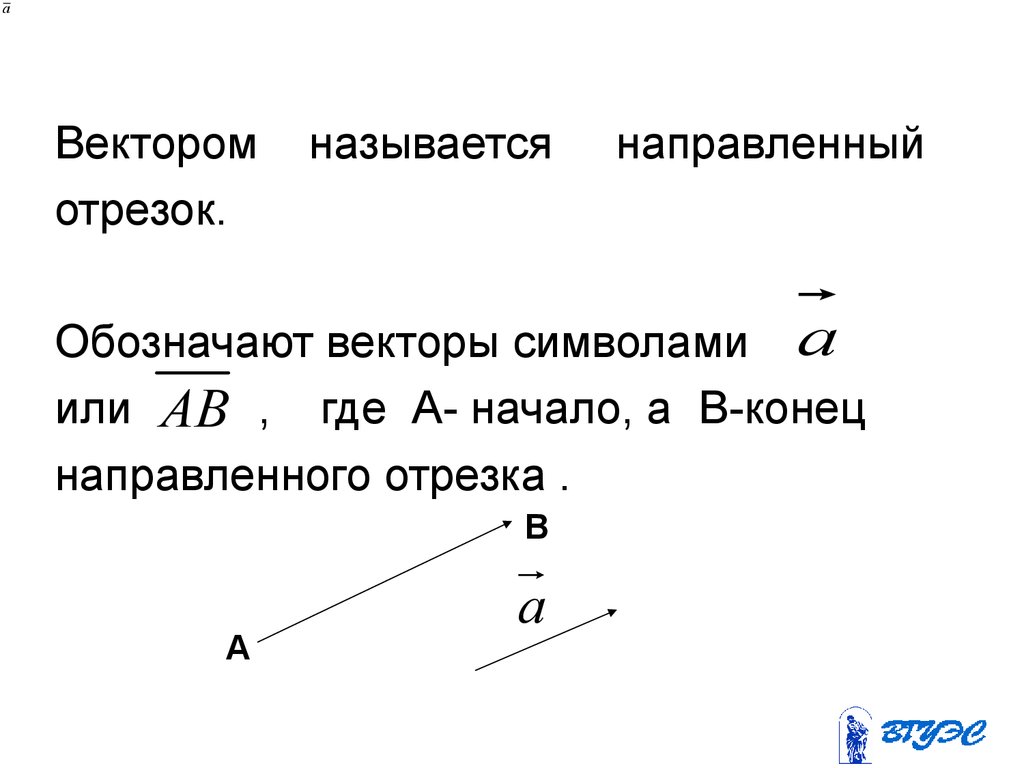
aВектором
отрезок.
называется
направленный
Обозначают векторы символами a
или AB , где А- начало, а B-конец
направленного отрезка .
В
А
a
3.
• Нулевым вектором (обозначается 0 )называется вектор, начало и конец
которого совпадают.
• Расстояние между началом и концом
вектора называется его длиной, или
модулем или абсолютной величиной.
• Векторы называются коллинеарными,
если они расположены на одной прямой
или на параллельных прямых
4.
• Векторы называютсякомпланарными, если они параллельны
одной плоскости.
• Векторы называются равными,
если они сонаправлены и имеют
равные длины.
• Два вектора, имеющие равные длины,
коллинеарные и противоположно
направленные, наз. противоположными.
5.
• Вектор, длина которого равна 1,называется единичным вектором или
ортом.
• Ортом вектора a называется
соноправленный ему вектор и
обозначается
a0
6. Линейные операции над векторами
7.
Линейными операциями называютоперации сложения и вычитания
векторов и умножения вектора на
число.
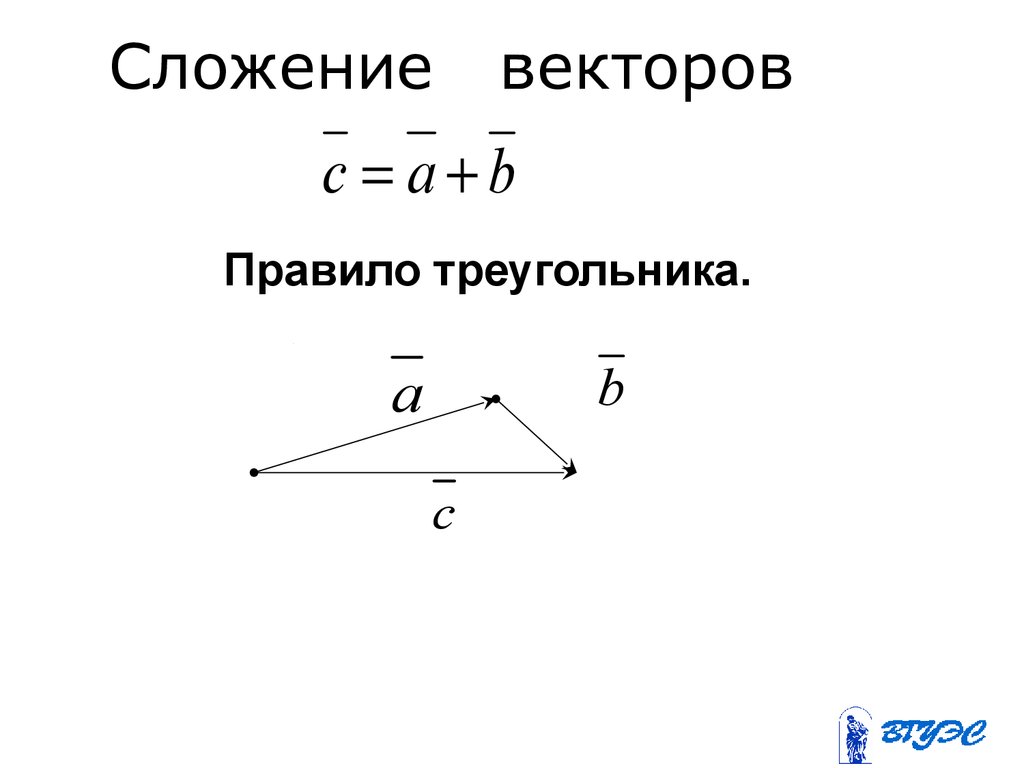
8. Сложение векторов
c a bПравило треугольника.
c
b
a
c
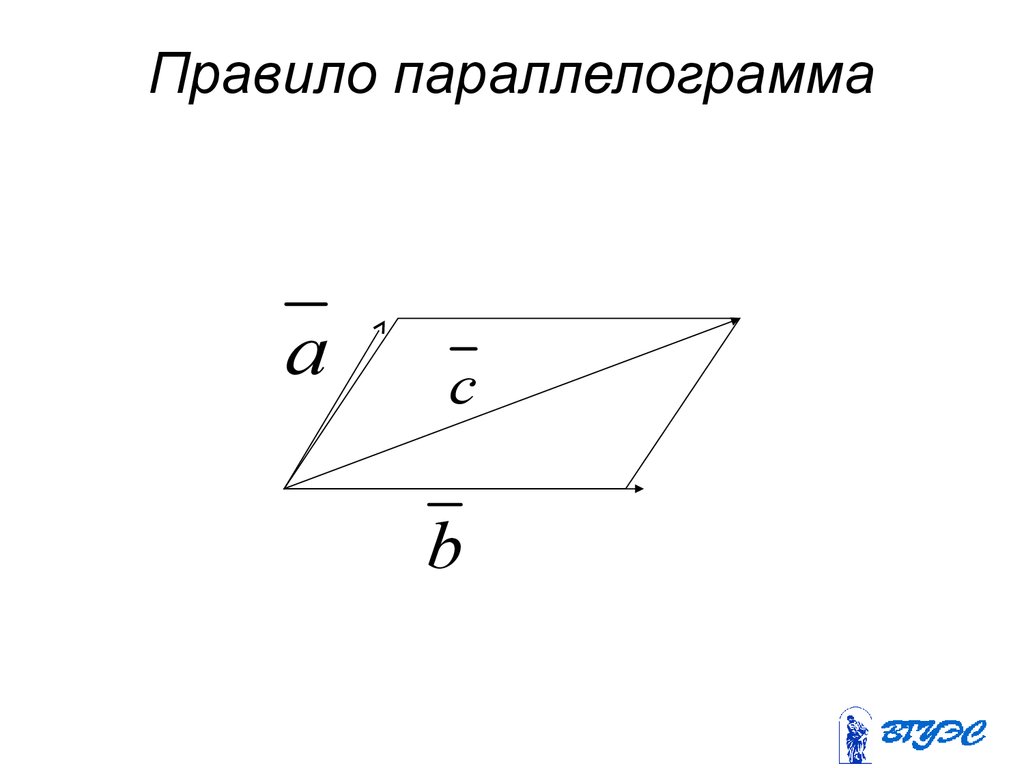
9. Правило параллелограмма
ac
b
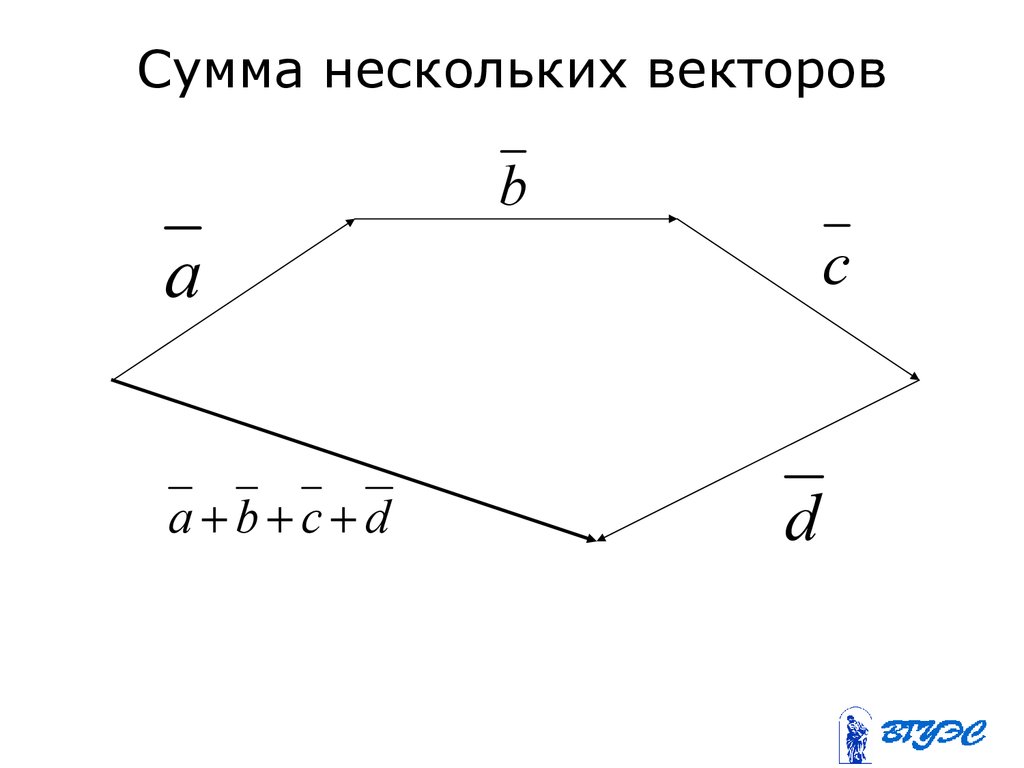
10. Сумма нескольких векторов
bc
a
a b c d
d
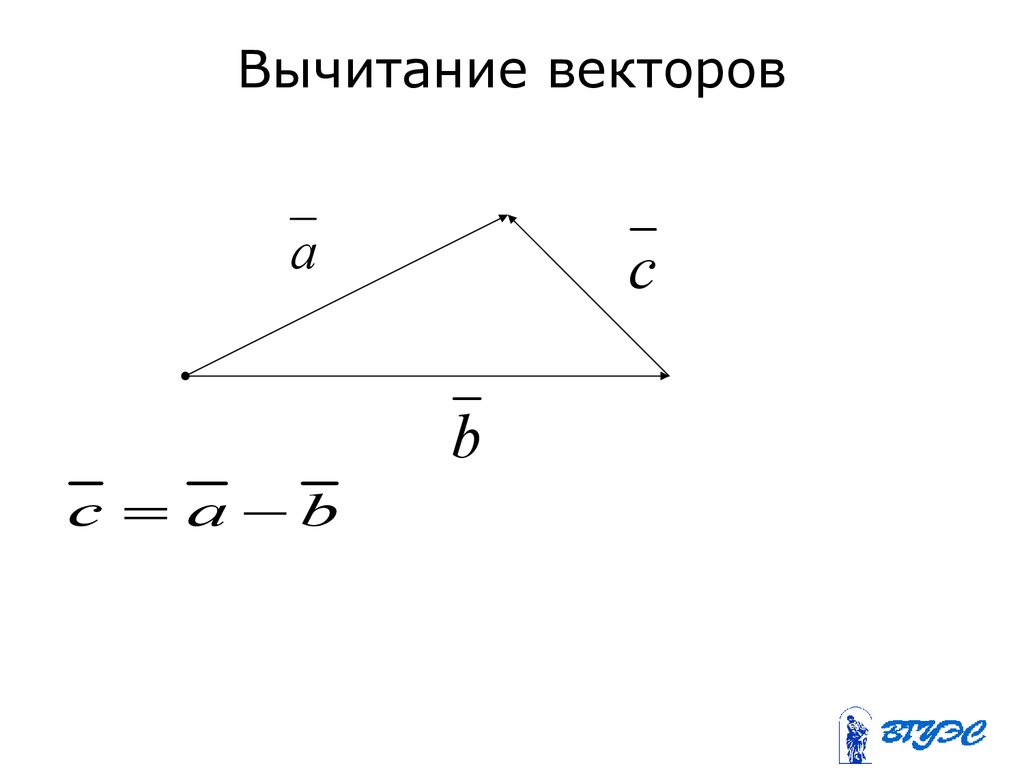
11. Вычитание векторов
ac
b
c a b
12. Свойства
a b b aa 0 a
13.
a (b c) (a b) ca ( a) 0
14. Умножение вектора на число
Произведением вектораaна
действительное число называется
b a
b
вектор
(обозначают
),
определяемый следующими условиями:
b a
1.
,
2. b a при
0 .
0и
b aпри
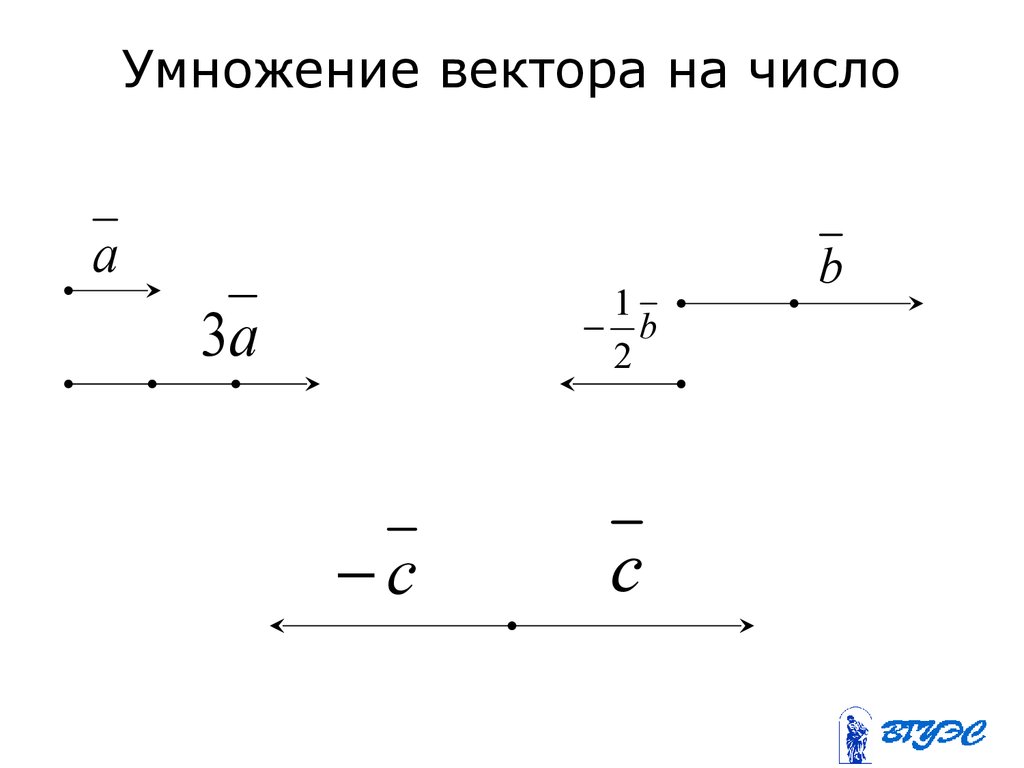
15. Умножение вектора на число
a1
b
2
3a
c
c
b
16. Свойства
( )a ( a) ( a)( )a a a
17.
( a b) a b1 a a
( 1) a a
18.
• Отсюда вытекает условие коллинеарностивекторов: два ненулевых вектора
коллинеарны тогда и только тогда, когда
имеет место равенство
b a, 0.
Если a 0 орт вектора a , то
a a a0
и тогда
a0
1
a
a
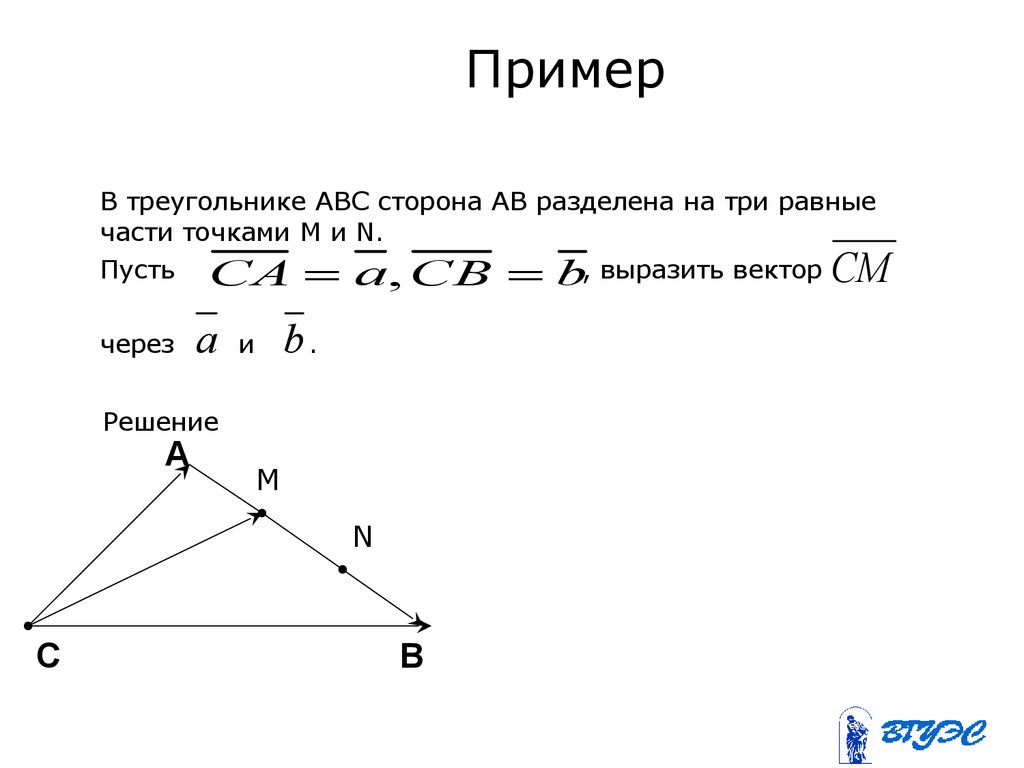
19. Пример
В треугольнике ABC сторона AB разделена на три равныечасти точками M и N.
Пусть CA a , CB b, выразить вектор
CM
через
a
b.
и
Решение
А
M
N
С
В
20.
1AM AB,
3
AB b a,
1
1
1
2
1
CM CM AM a b a a b a a b
3
3
3
3
3
21. Угол между двумя векторами
22.
• Углом между векторами наз-сянаименьший угол 0 , на который
надо повернуть один из векторов до его
совпадения со вторым.
• Под углом между вектором и осью понимают
угол между вектором и единичным вектором,
расположенным на оси
a
l0
l
23. Проекция вектора на ось и составляющая вектора на оси
24.
BA
l0
A1
)
B1
l
25.
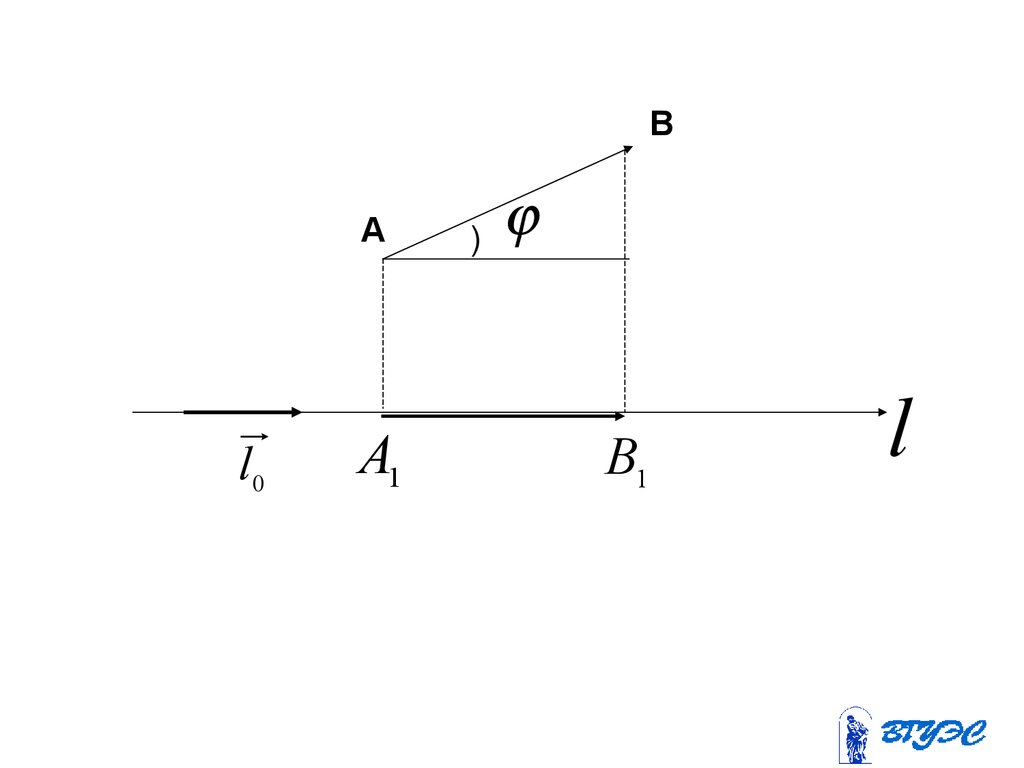
l• Проекцией вектора AB на ось
называется разность x2 x1 между
координатами проекций конца и начала
вектора на эту ось.
Обозначается
прl AB .
26.
• Если - острый, то прl AB 0;если - тупой, то прl AB 0;
если , то прl AB 0.
2
27.
• Вектор A1 B1 наз. составляющей вектораAB по оси l и обозначается
A1 B1 состl AB прl AB l0 x2 x1 l0
28.
1) пр l AB АВ cos AB, l ;3) пр a пр a.
2) прl a b прl a прl b;
l
l
29. Линейная зависимость векторов
30.
• Векторыa1 , a2 ,..., an
наз-ся линейно
зависимыми, если существуют числа
1 , 2 ,..., n
не все равные 0, для
которых имеет место равенство
1 a1 2 a2 ... n an 0 (*)
31.
3n
2
a1 a2 a3 ... an
1
1
1
a1 2 a2 3 a3 ... n an
2 a2 3 a3 ... n an линейная
комбинация векторов
32.
• Векторыa1 , a2 ,..., an
наз-ся
линейно независимыми, если равенство
1 a1 2 a2 ... n an 0
выполняется только при
1 2 ... n 0
33.
• Для того чтобы векторы были линейнозависимы, необходимо и достаточно,
чтобы хотя бы один из этих векторов
можно было представить в виде
линейной комбинации остальных.
• Всякие три вектора на плоскости
линейно зависимы.
34.
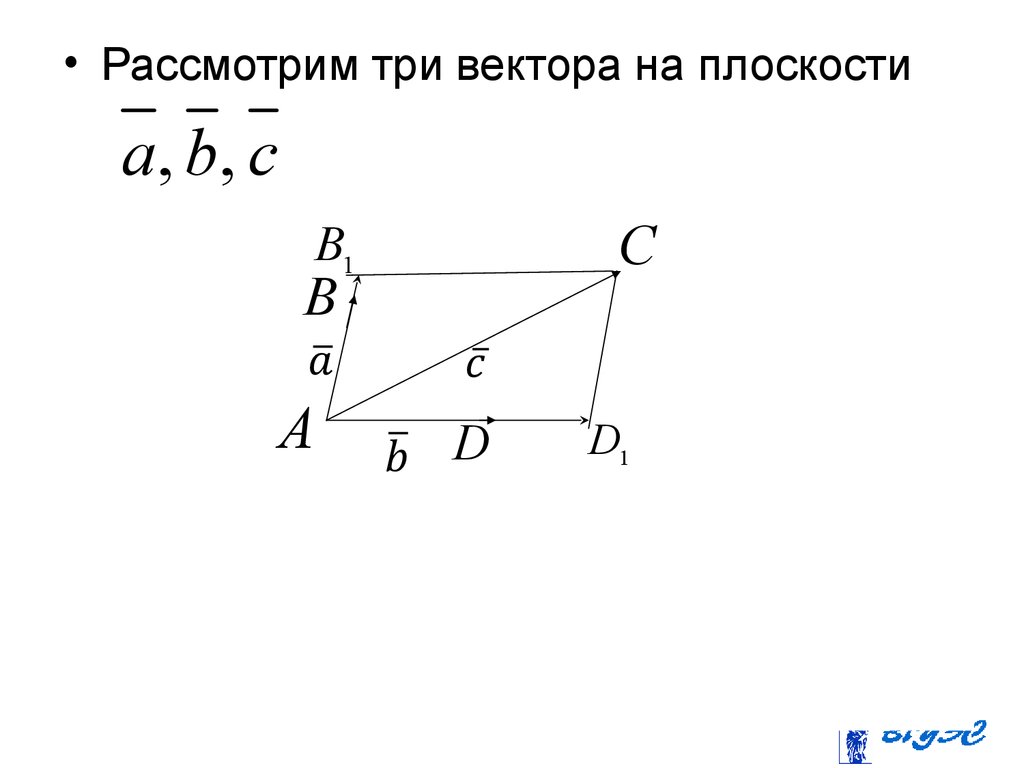
• Рассмотрим три вектора на плоскостиa, b, c
C
B1
B
A
D
D1
35.
AC AB1 AD1AB1 1 AB
AD1 2 AD
AC 1 AB 2 AD
36.
• Для того чтобы два вектора былилинейно независимы, необходимо и
достаточно, чтобы они были
неколлинеарны.
• Для того чтобы три вектора в
пространстве были линейно
независимы, необходимо и достаточно,
чтобы они были некомпланарны.
37.
• Максимальное число линейнонезависимых векторов на плоскости
равно двум.
• Максимальное число линейно
независимых векторов в пространстве
равно трём.
38. Базис на плоскости и в пространстве
39.
• Базисом на плоскости называютдва любых линейно независимых
вектора.
Т. Разложение любого вектора
на плоскости по базису b, c
является единственным
a
40.
• Базисом в пространстве называюттри любых линейно независимых
вектора.
Т. Разложение любого вектора a
в пространстве по базису b, c, d
является единственным
41. Прямоугольный декартовый базис
42.
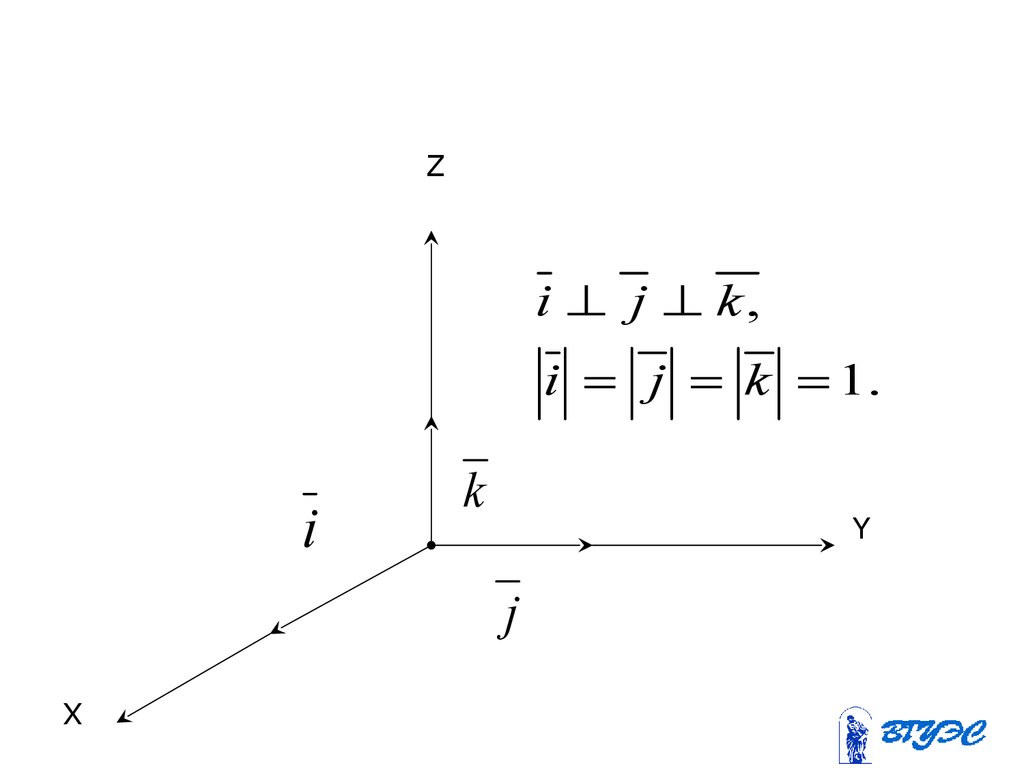
Zi j k,
i j k 1.
i
k
Y
j
X
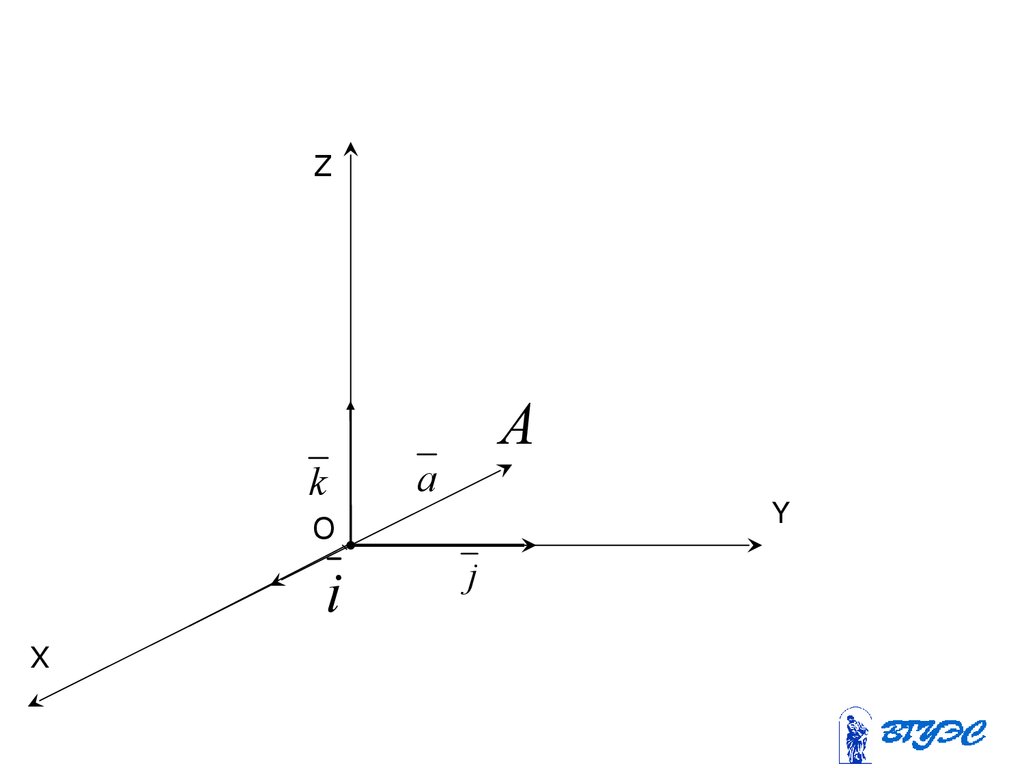
43.
Zk
A
a
Y
O
i
X
j
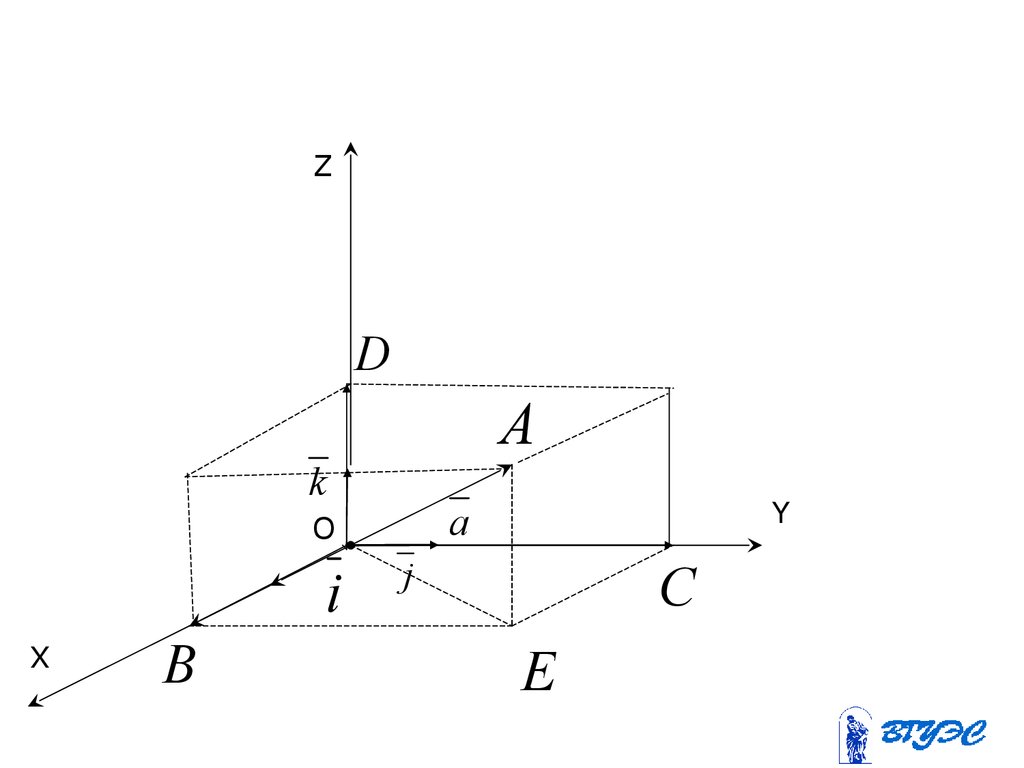
44.
ZD
A
k
i
X
B
Y
a
O
j
C
E
45.
OA OB BE EAOA OB OD OC
OB прox a i
прox a a x
OC прoy a j
прoy a a y
OD прoz a k
прoz a a z
a ax i a y j az k
46. Линейные операции над векторами в координатной форме
47.
• Пустьa ax i a y j az k
b b x i b y j bz k
тогда:
1) a b (a x
2)
bx ) i ( a y b y ) j ( a z bz ) k
a a x i a y j a z k
ax a y az
3) a || b
bx b y bz
4)
a a a a
2
x
2
y
2
z
48.
A x1 ; y1 ; z1B x2 ; y 2 ; z 2
AB x2 x1 i y 2 y1 j z 2 z1 k
AB
x
x1 y 2 y1 z 2 z1
2
2
2
2
49. Направляющие косинусы
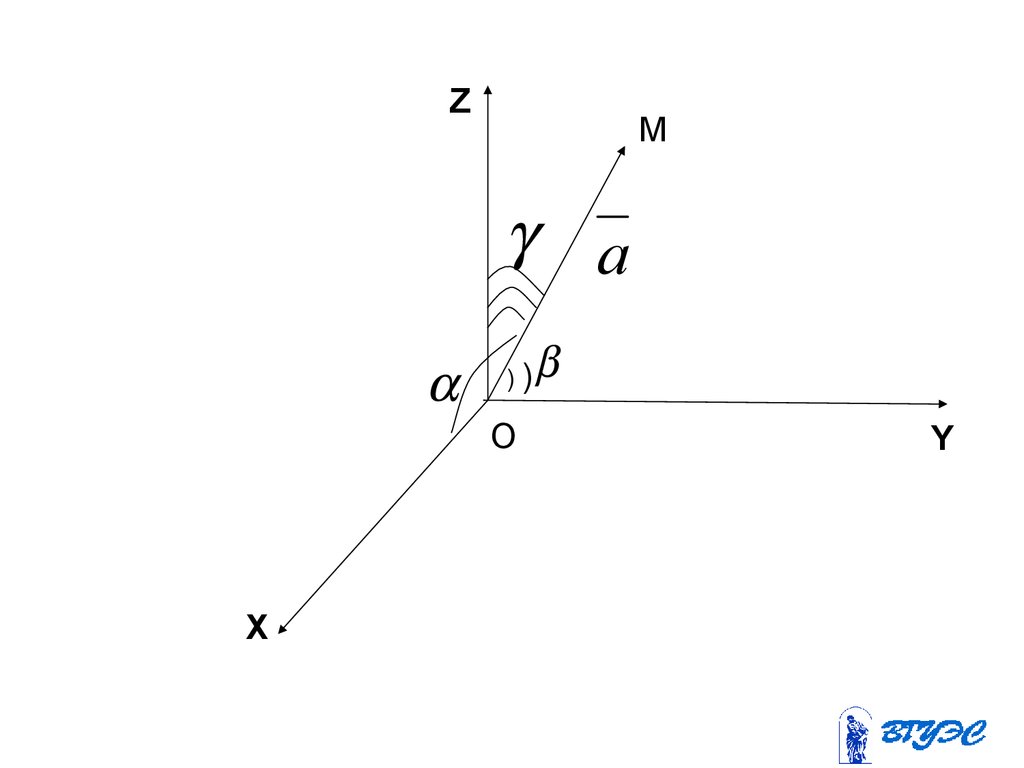
50.
ZM
a
))
O
X
Y
51.
• Пусть дан векторa ax i a y j az k
a x прox a a cos
a y прoy a a cos
a z прoz a a cos
52.
axcos
a
cos
ay
a
az
cos
a
53.
22
2
cos cos cos 1
54. Координаты единичного вектора
a 0 cos , cos , cos ,55. Пример
Найти косинусы углов, которые, вектор AB составляет сосями координат, если А (1,2,3) и В (2,4,5).
Решение.
AB 2 1;4 2;5 3 1;2;2 ,
AB 12 22 22 3,
тогда
1
2
2
cos , cos , cos
3
3
3
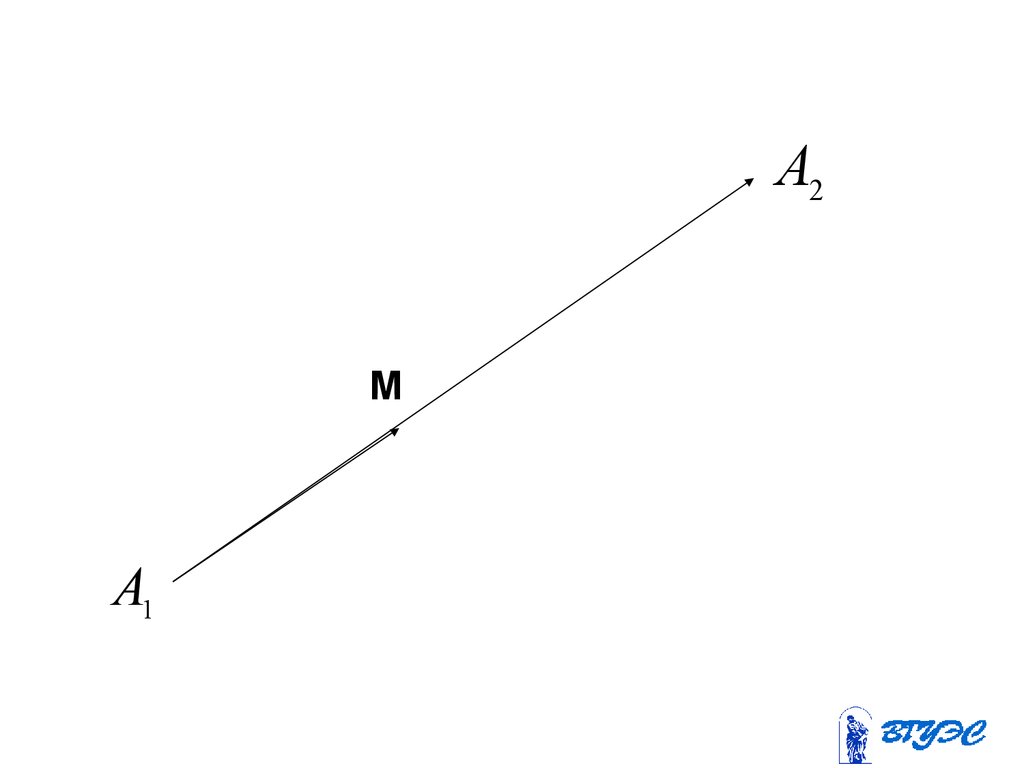
56. Деление отрезка в данном отношении
57.
A2M
A1
58.
A1 x1 ; y1 ; z1A2 x2 ; y 2 ; z 2
M x; y; z
A1 M
MA2
59.
x1 x 2x
1
y1 y 2
y
1
z1 z 2
z
1
60.
• Если1,
т.е.
A1 M MA2
x
1 x2
x
2
y1 y2
y
2
z
1 z2
z
2
, то
61. Скалярное произведение векторов
Скалярным произведением векторовназывается
произведение
их
модулей на косинус угла между
ними.
62.
a b a b cos63. Условие перпендикулярности векторов
a b a b 064.
a b a прa ba b b прb a
65. Проекция вектора на вектор
a bпрb a
b
66. Угол между векторами
cosa b
a b
x1 x2 y1 y 2 z1 z 2
.
2
x y z x y z2
2
1
2
1
2
1
2
2
2
2
67. Физический смысл скалярного произведения
Работа постоянной силы напрямолинейном участке пути равна
скалярному произведению вектора
силы на вектор перемещения.
68. Физический смысл скалярного произведения
Fl
A F l
69. Свойства скалярного произведения
1) a b b a2) (a b) ( a) b a ( b)
70.
23) a a
a
2
a
2
71.
• Пусть даны два вектораa ax i a y j az k
b bx i b y j b z k
72.
Найдем скалярное произведение этихвекторов
(ax i a y j az k ) (bx i by j bz k )
= a x bx
a y by az bz
2
2
i i i i 1
2
2
2
2
j j j j 1
k k k k 1
i j 0
j k 0
i k 0
73. Пример
Дан векторугол
c 2a 3b , причем a 4
между векторами
Найти модуль вектора
c.
a
и
b
равен
,
b 5
60 0.
,
74.
Решениес
a a
2a 3b
2
2
с
2
2
4a 12a b 9b .
2
4 16
2
2
2
b b 5 25,
a b a b cos 4 5 cos 60
то
2
c
4 16 12 10 9 25
2
0
10,
409 .
75. Векторное произведение векторов
76.
• Векторным произведением вектора aна вектор b наз. вектор c a b,
удовлетворяющий следующим условиям:
1)
2)
c a b sin
c
a
c
b
3)векторы образуют правую тройку
77. Понятие «правой» тройки векторов
a , b, cТройку векторов
называют правой, если
направление вектора c таково, что, смотря из его конца
вдоль вектора, кратчайший поворот от вектора
a
к вектору b будет виден против движения часовой
стрелки.
с
a , b, с
b
- правая тройка
a
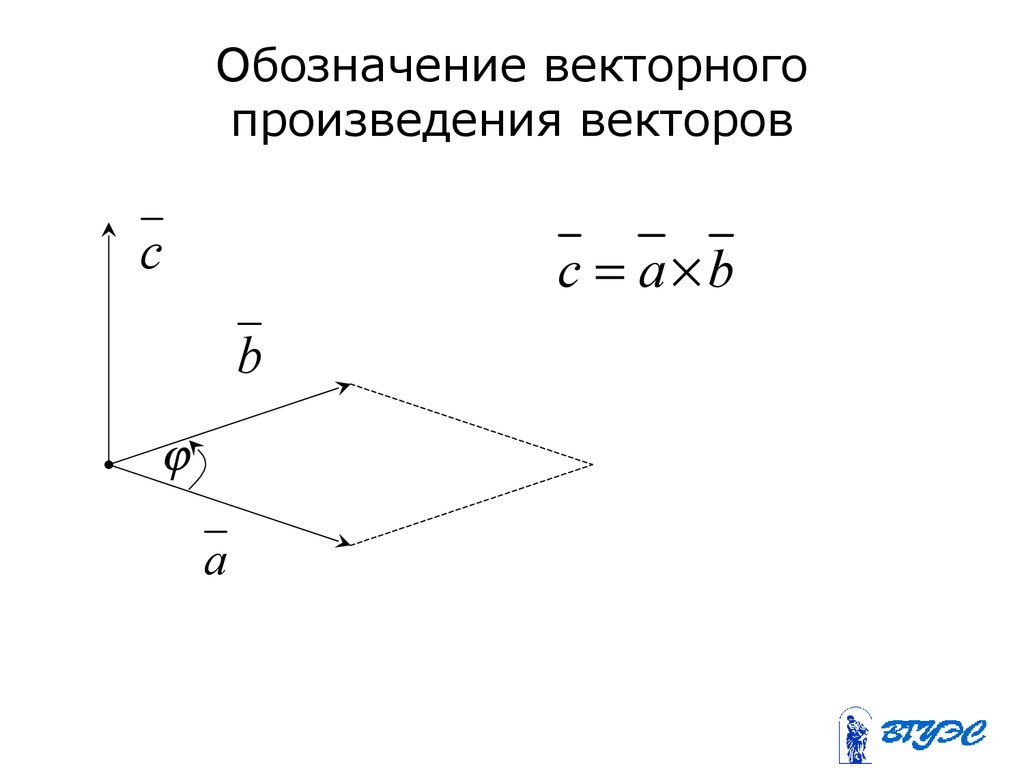
78. Обозначение векторного произведения векторов
cc a b
b
a
79. Свойства векторного произведения
a b b aa b 0 a 0
или
b 0 или a b
a a 0
80. Свойства векторного произведения
( a b) c a c b c( a b ) ( a ) b a ( b )
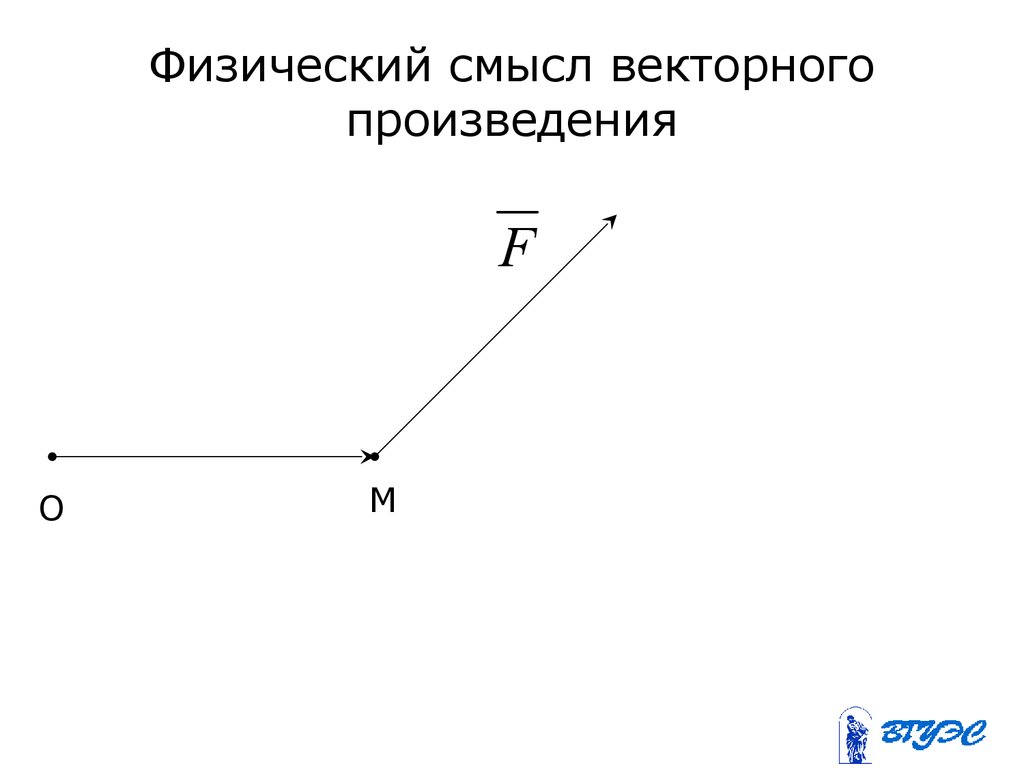
81. Физический смысл векторного произведения
FO
M
82. Физический смысл векторного произведения
Если F – сила, приложенная к точке М,то момент этой силы относительно точки
О равен векторному произведению
векторов F и OM .
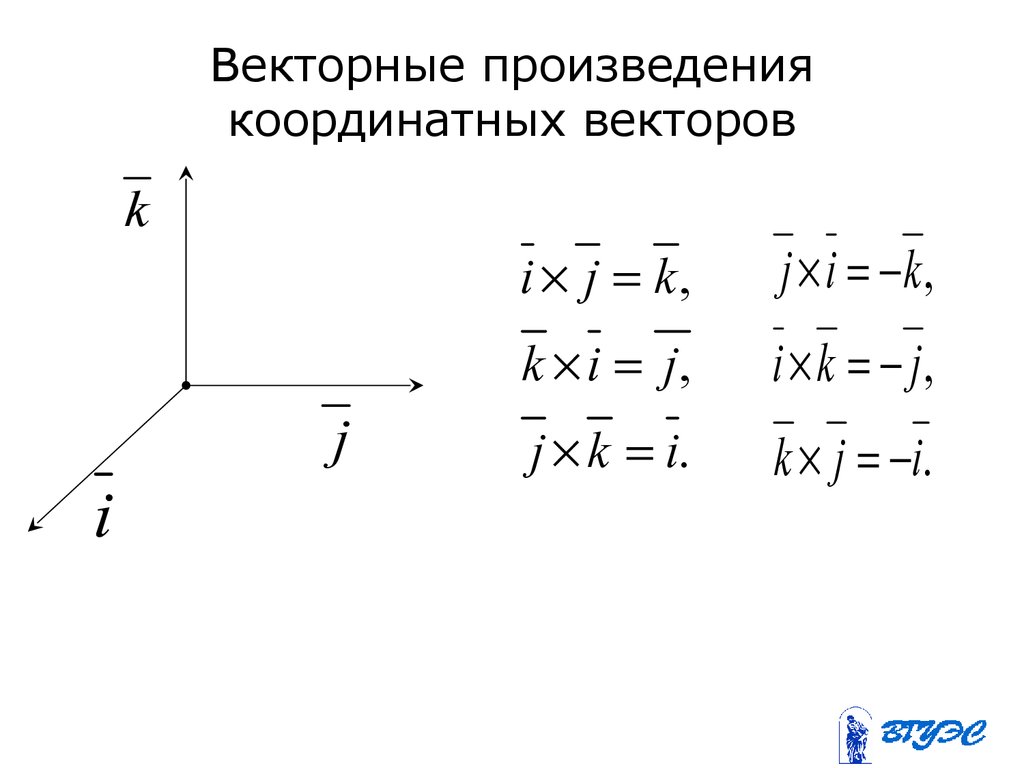
83. Векторные произведения координатных векторов
kj
i
i j k,
j i k ,
k i j,
i k j,
j k i.
k j i.
84.
a b ax i a y j az k bx i by j bz kaxbx i i axby i j axbz i k a ybx j i
a yby j j a ybz j k az bx k i az by k j
az bz k k
85.
axby k axbz j a y bx k a y bz i az bx j az by ia y bz az by i axbz az bx j axby a y bx k
ay
by
az
ax
i
bz
bx
ax
az
j
bx
bz
ay
k
by
86. Векторное произведение в координатной форме
ia b ax
bx
j
k
ay
az
by
bz
87. Пример
Найти векторное произведение векторовa 2i 3 j k ,
b 3i j 4k .
Решение
i
a b 2
k
3 1
1
i
1 4
3 1 4
2
1
3 4
j
3
j
2
3
3 1
k 13i 5 j 11k .
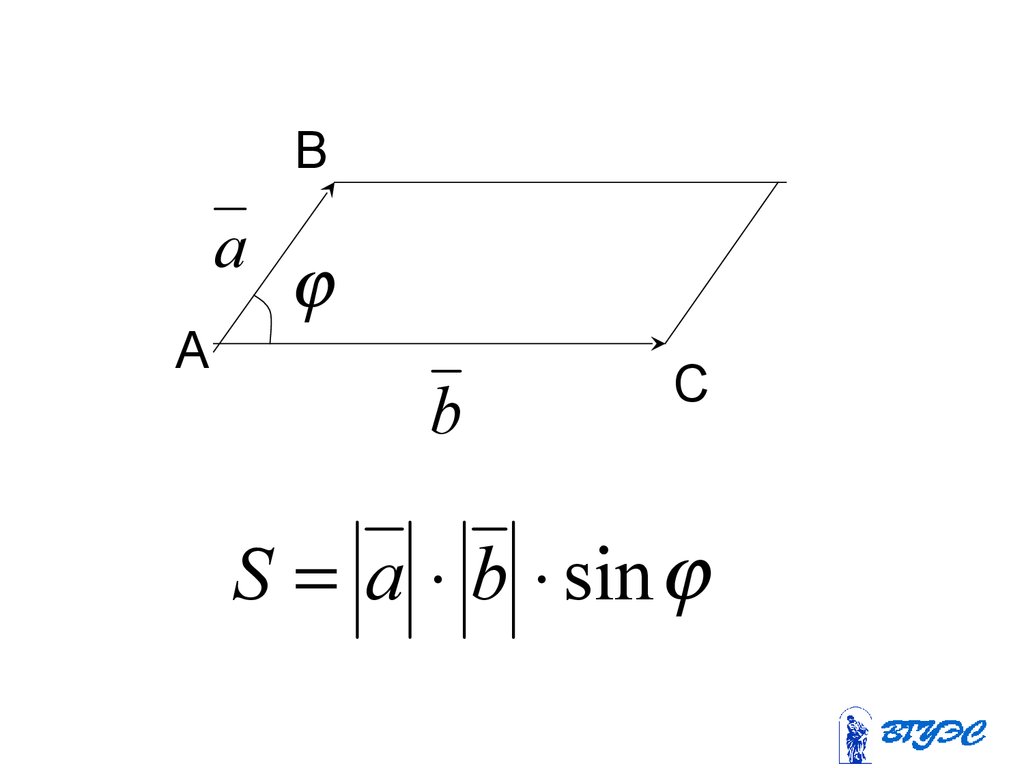
88.
Ba
A
b
C
S a b sin
89. Площадь параллелограмма
S пар a b90. Площадь треугольника
1S a b
2
91. Пример
Найти2a 3b a 2b ,
если
Решение
a 2, b 1, 900.
2a 3b a 2b
2 a a 3 b a 4 a b 6 b b
7 b a 7 b a sin
7 1 2 sin 90 14.
0
92. Смешанное произведение
Смешанным произведением трёхвекторов называется произведение
вида :
( a b) c
93.
a bay
by
az
ax
i
bz
bx
ax
az
j
bx
bz
ay
by
k
c cx i c y j cz k
ay
abc
by
az
ax
cx
bz
bx
ax
az
cy
bx
bz
ay
cz
by
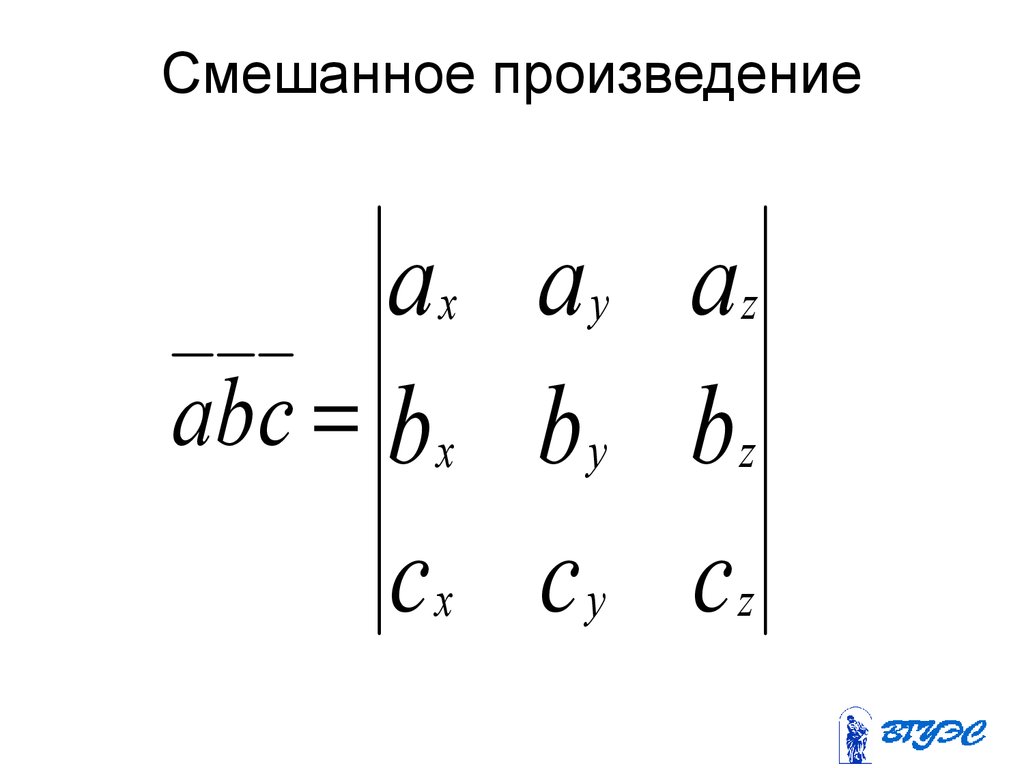
94. Смешанное произведение
ax a y azabc b x b y b z
cx c y cz
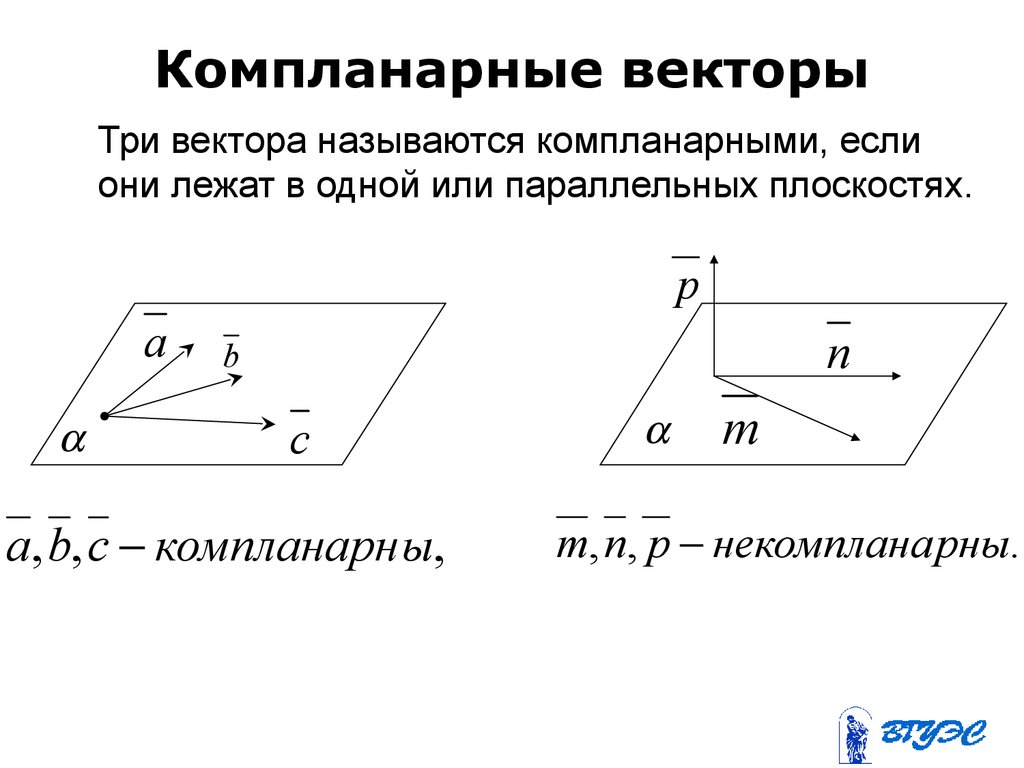
95. Компланарные векторы
Три вектора называются компланарными, еслиони лежат в одной или параллельных плоскостях.
p
a
n
b
c
a, b, c компланарн ы,
m
m, n, p некомплана рны.
96. Условие компланарности трёх векторов
Еслиa, b, c
компланарны, то
ax
bx
ay
by
az
bz 0.
cx
cy
cz
Элементами определителя являются координаты
векторов
a , b, c
97.
ca
b
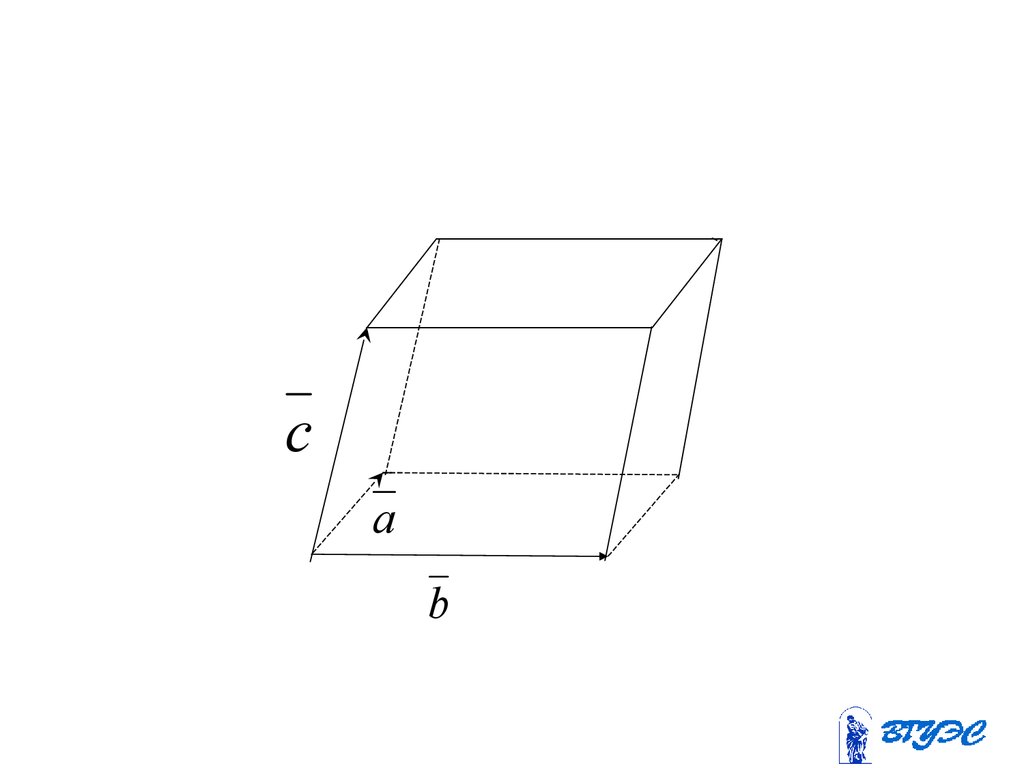
98. Объём параллелепипеда
V abc99. Объём тетраэдра
Vтет1
abc
6







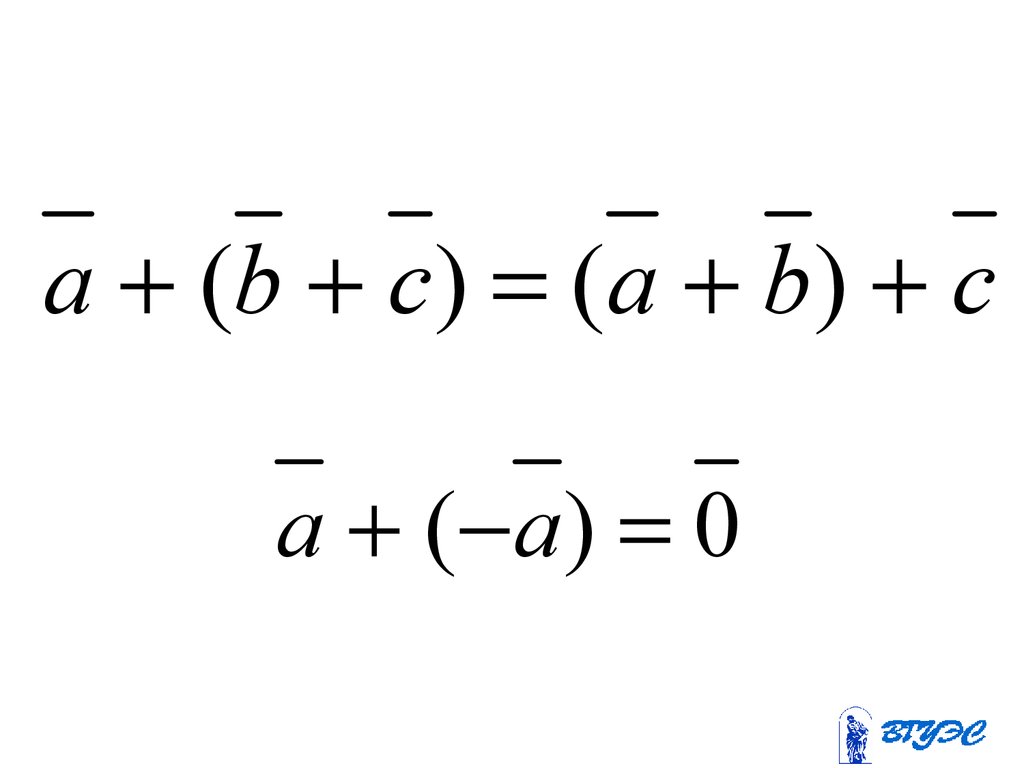

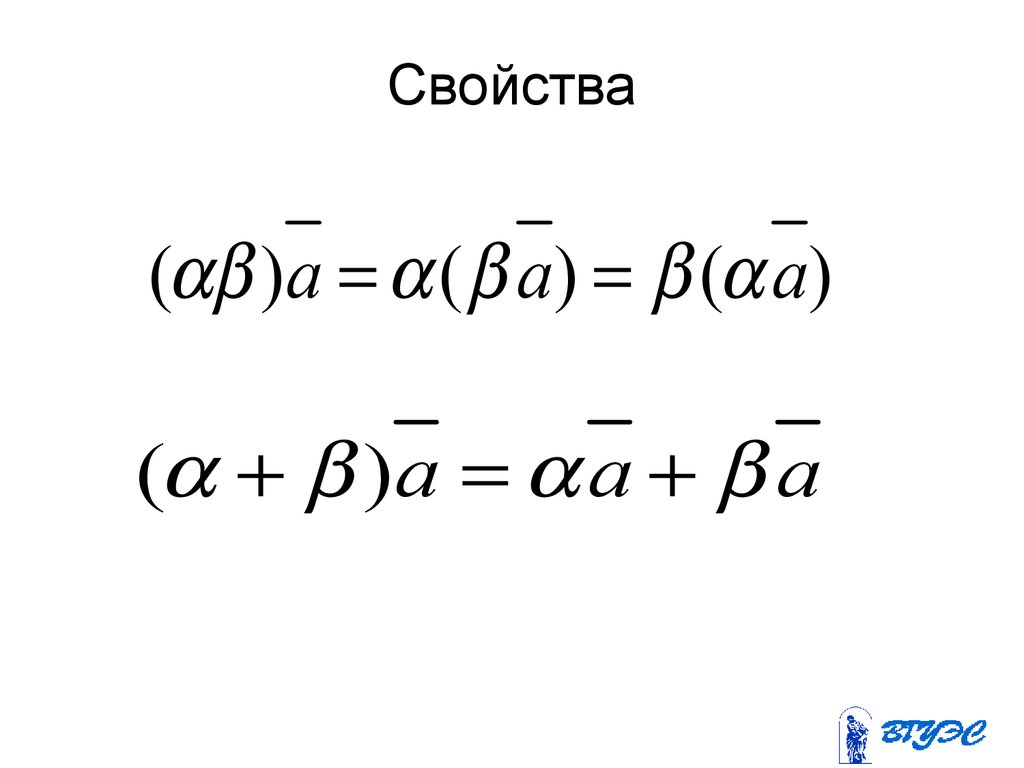
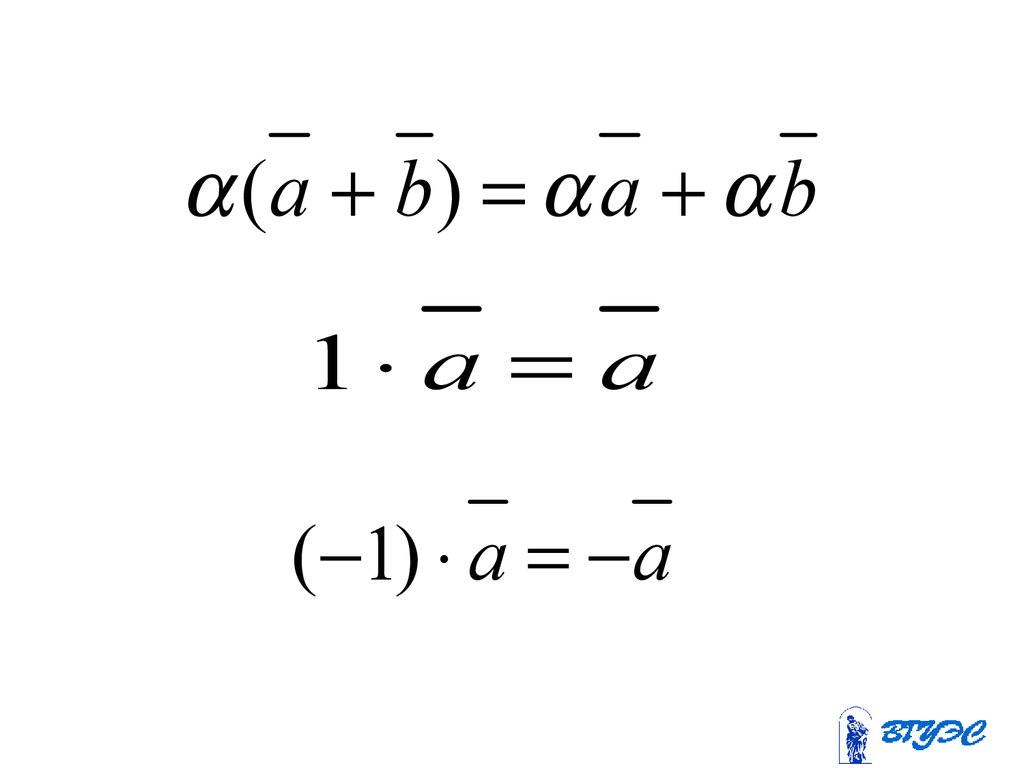

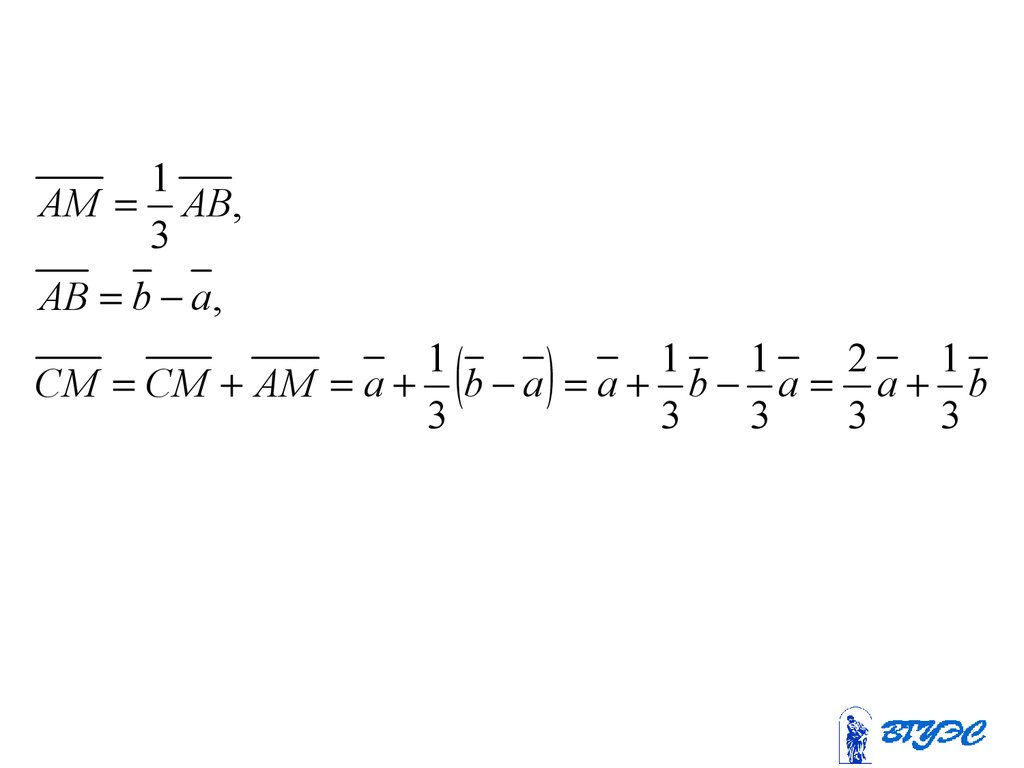






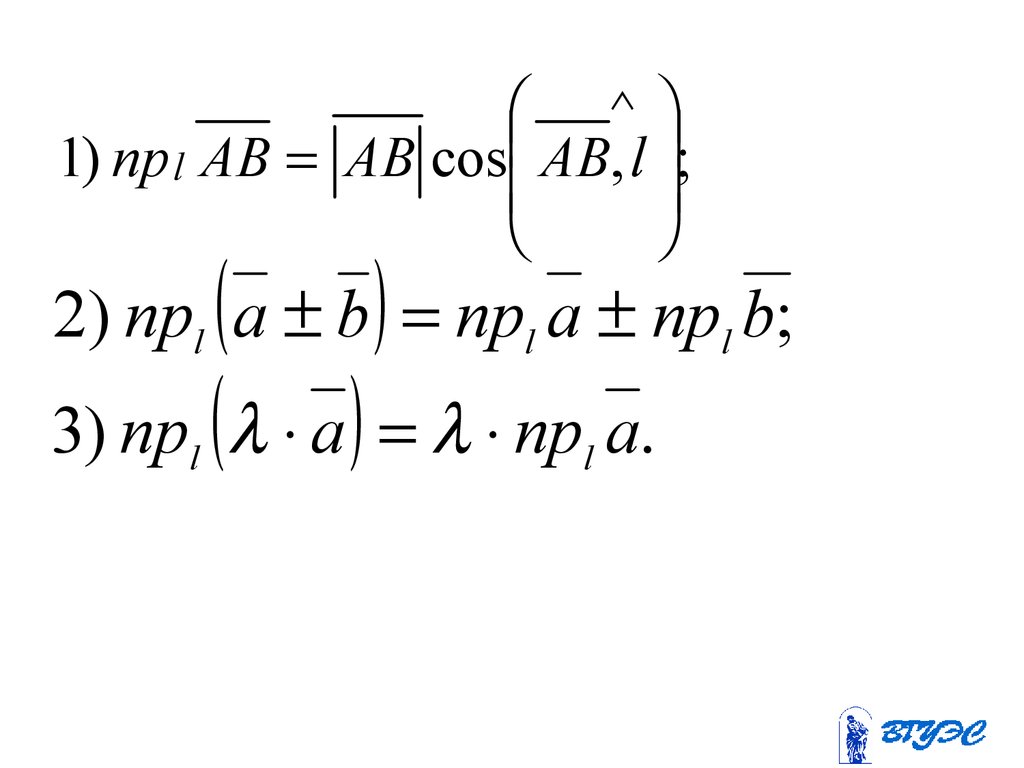












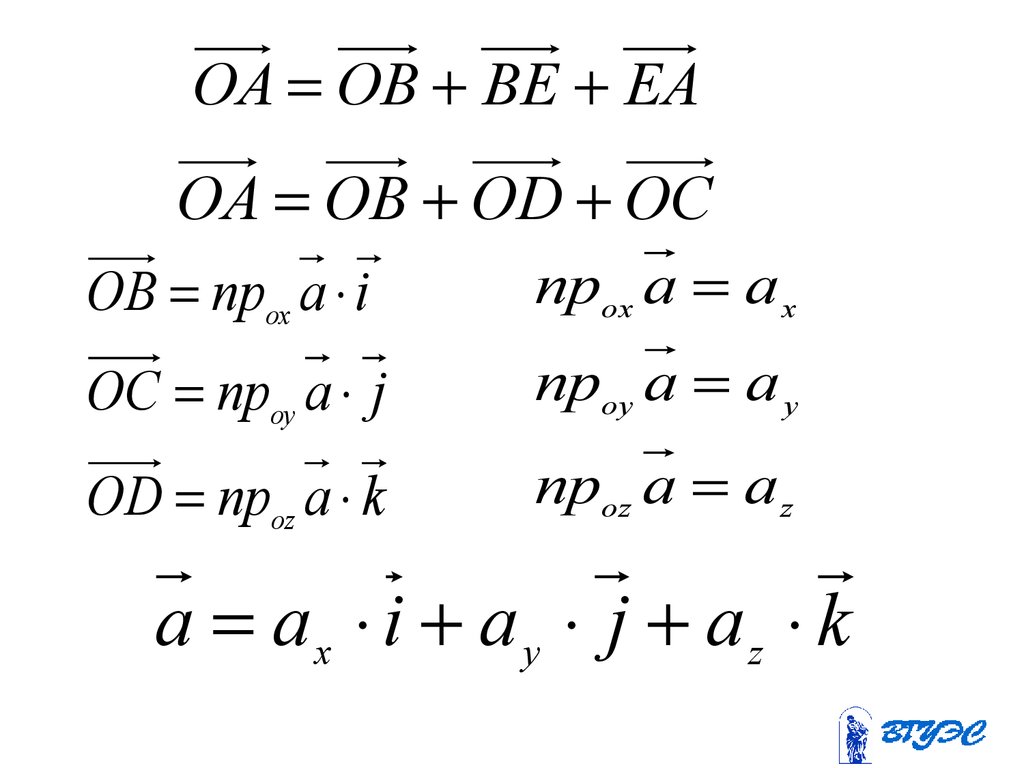

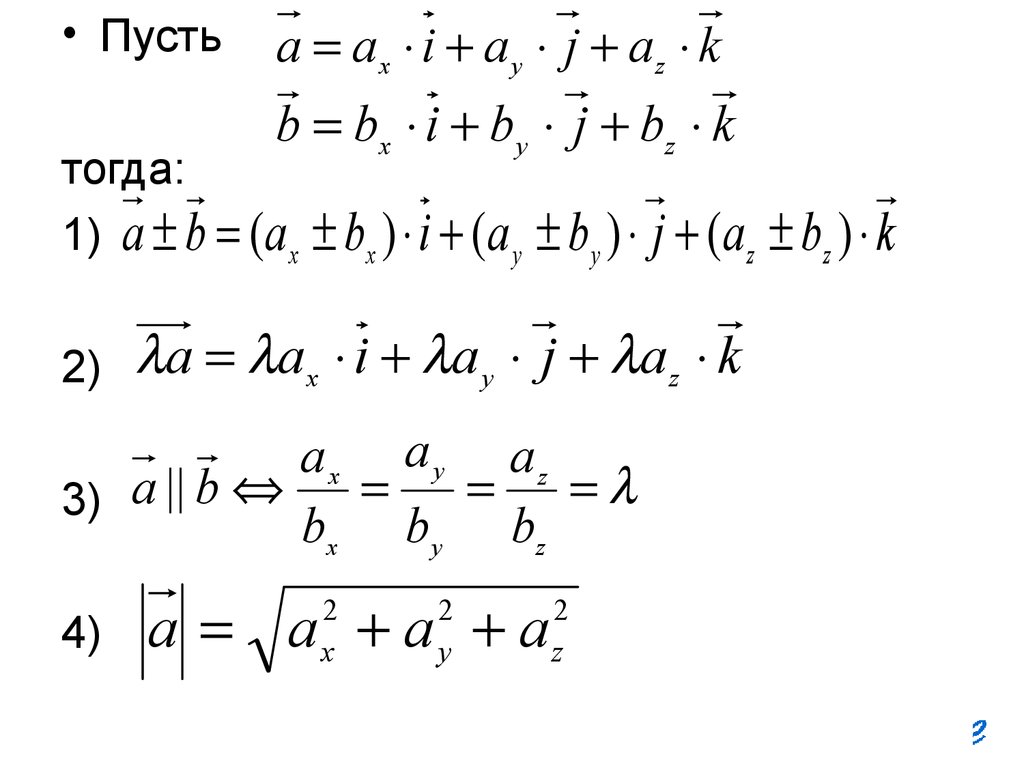
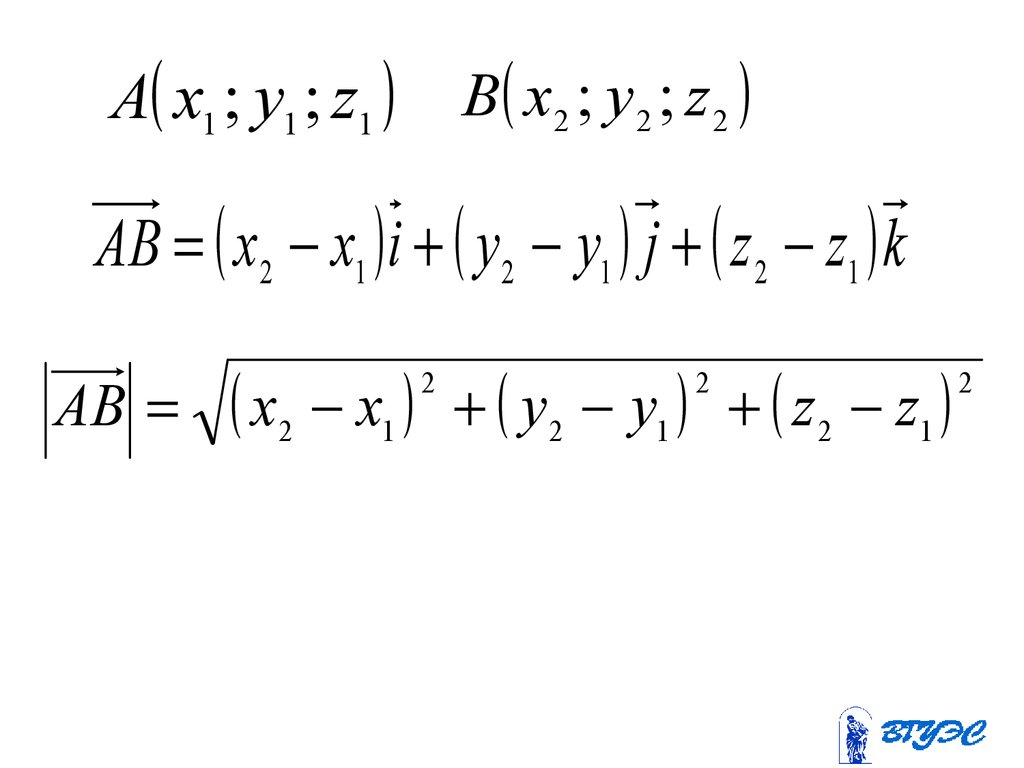

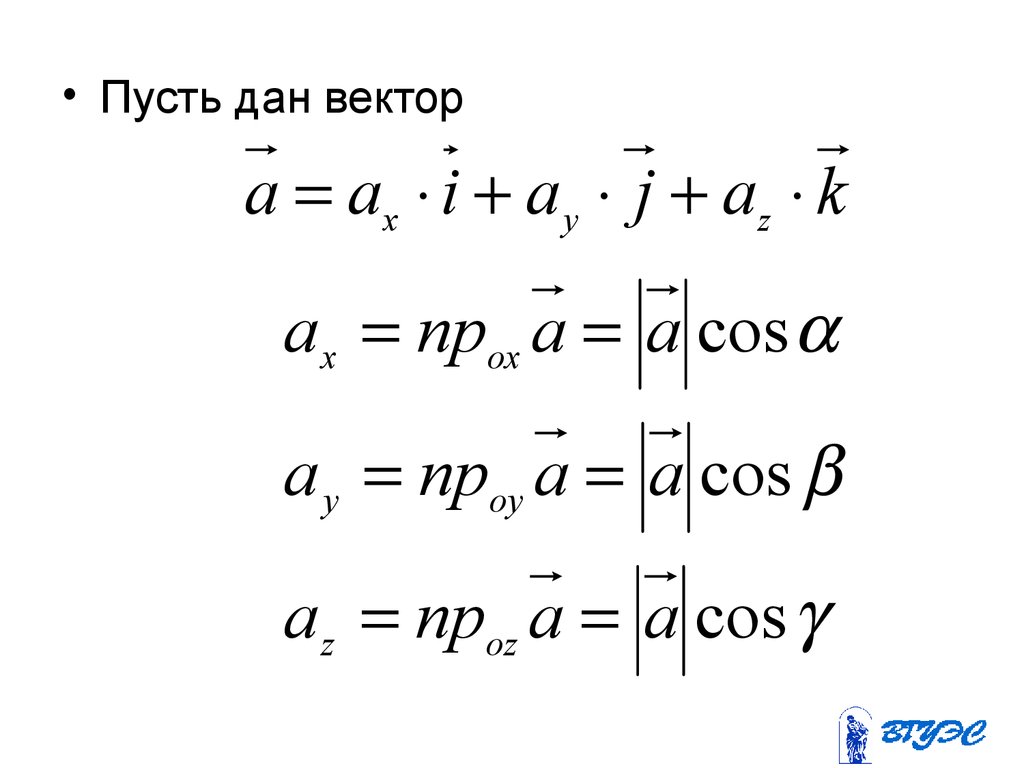
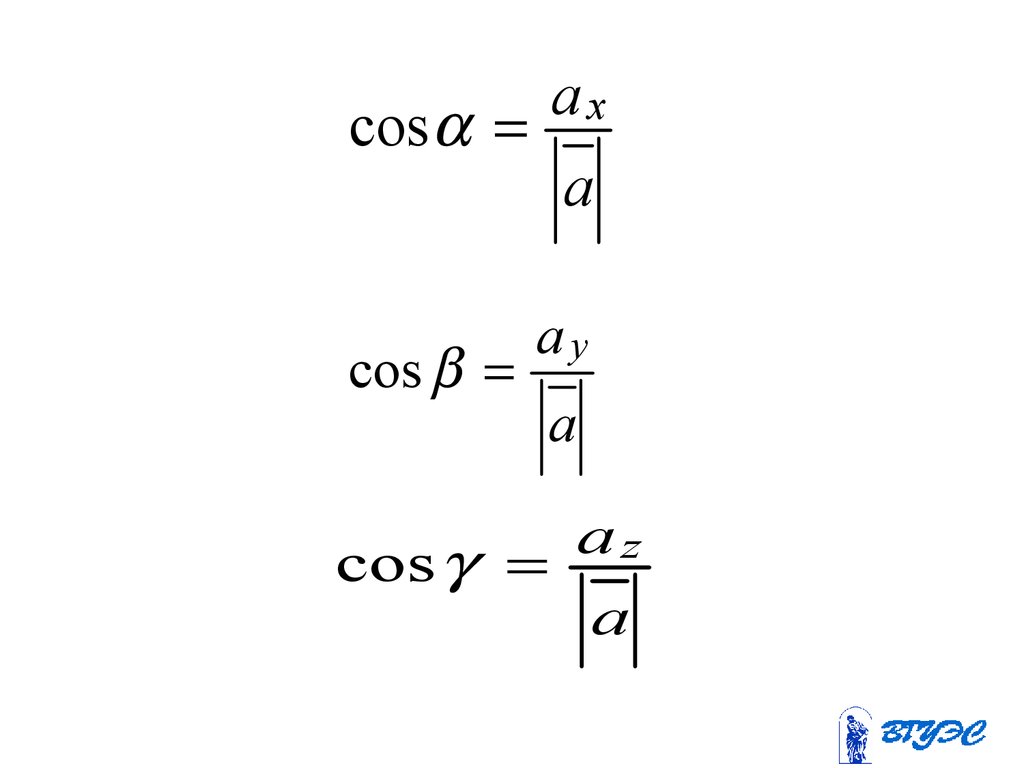
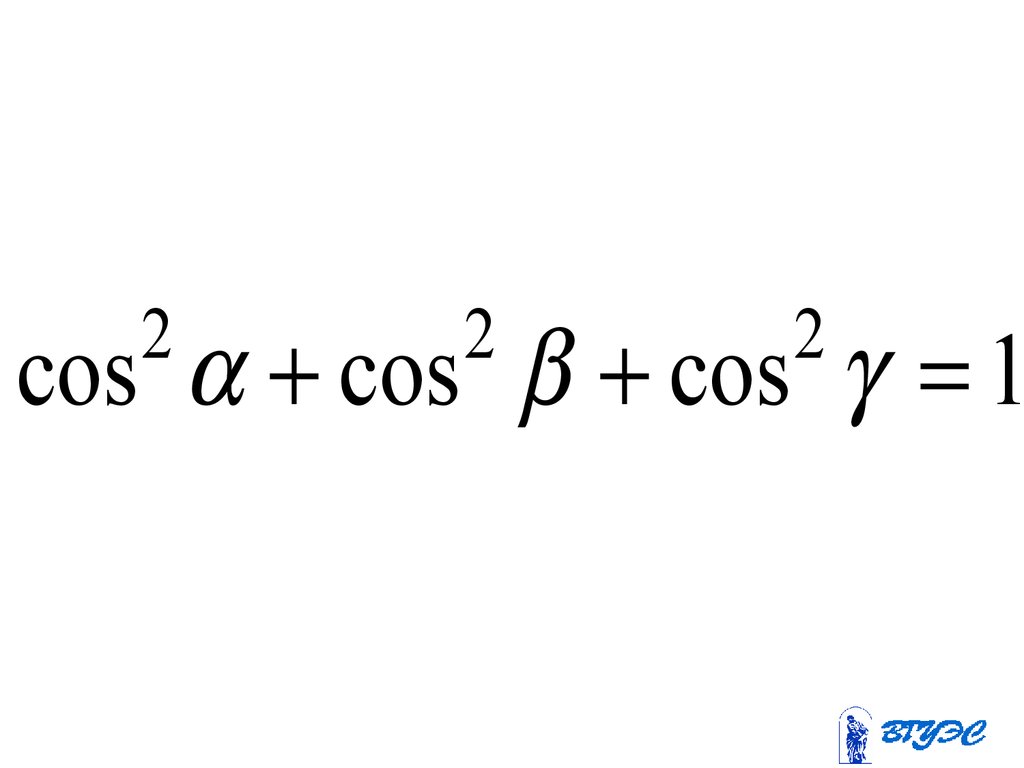



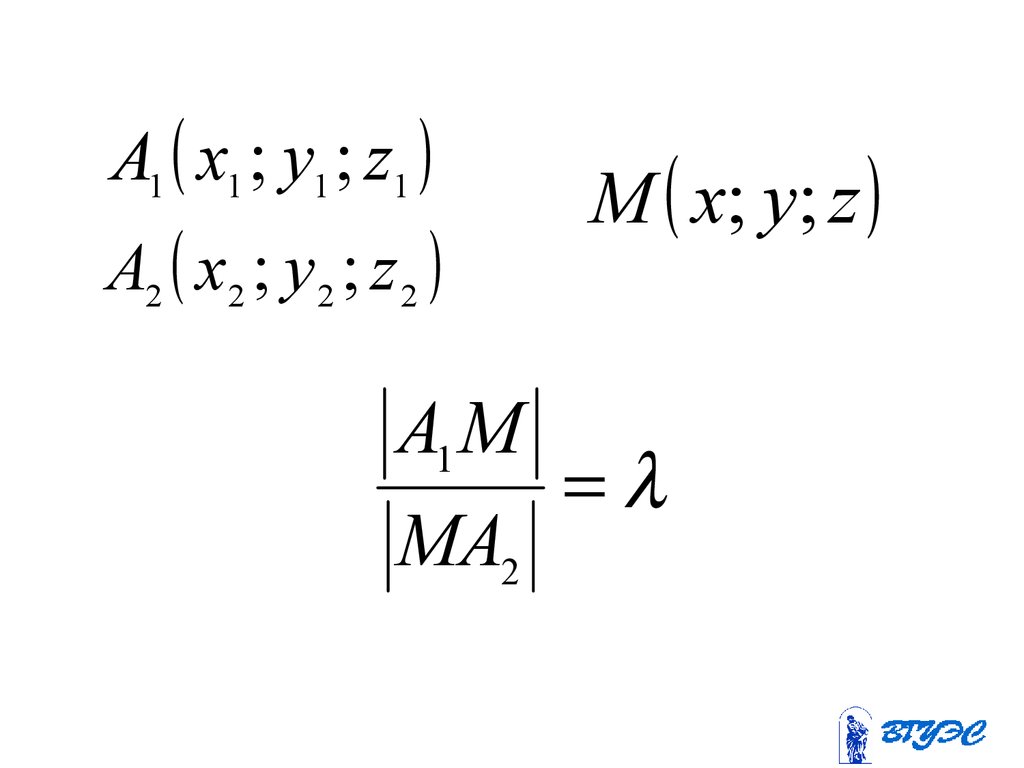
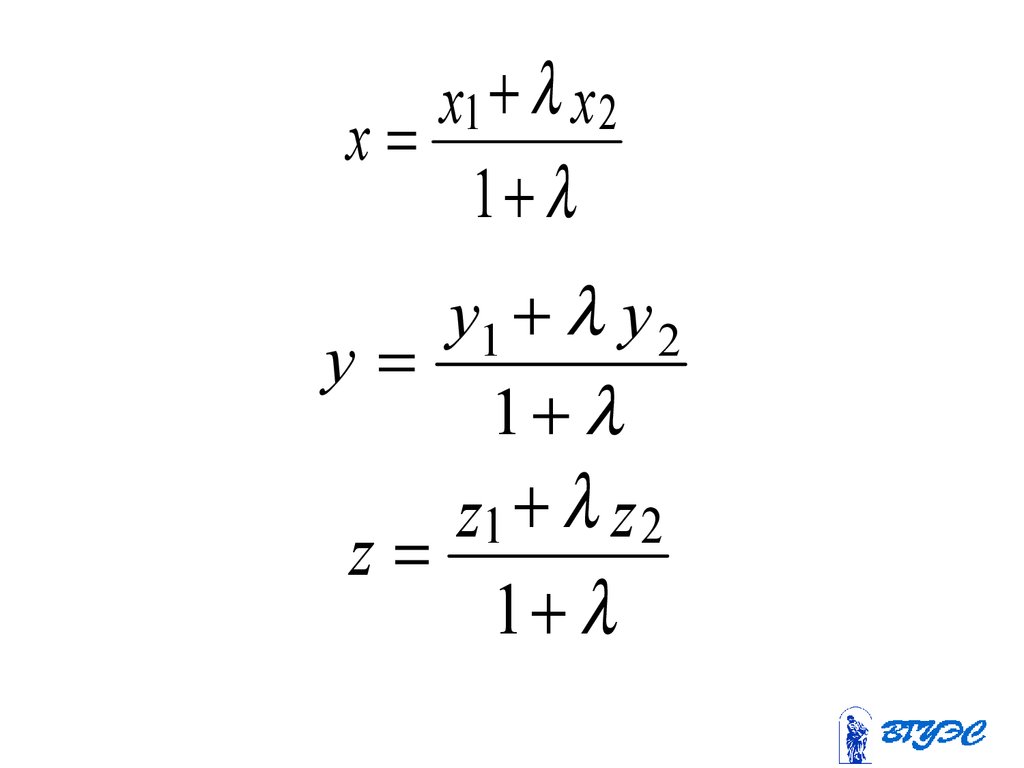
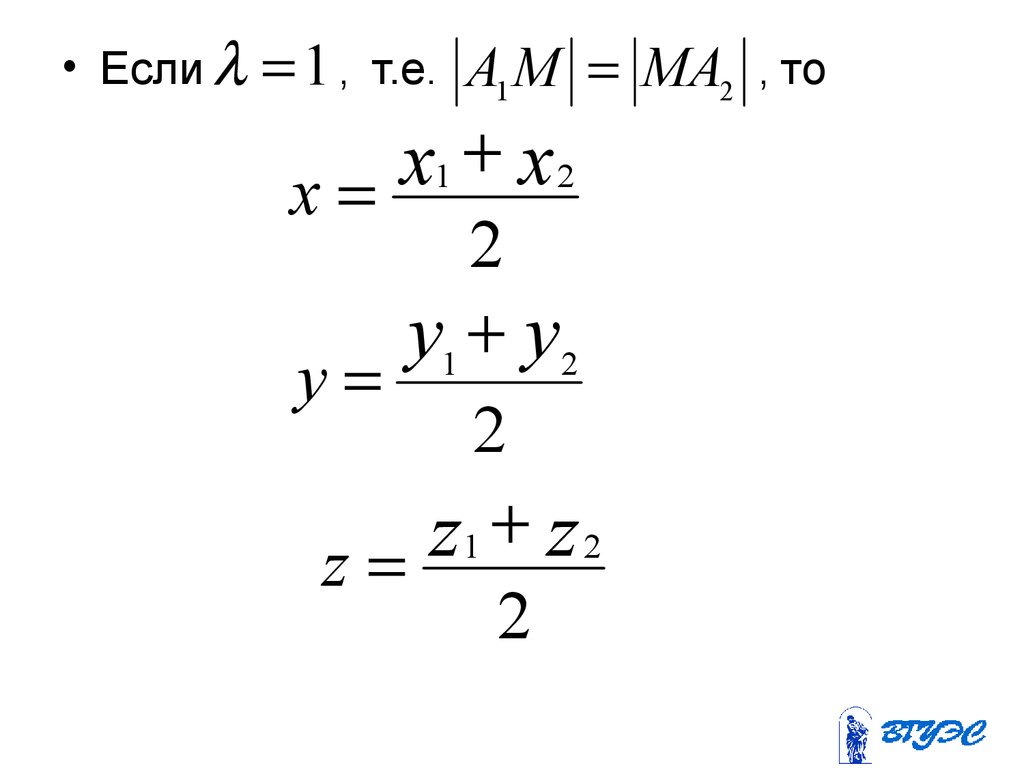

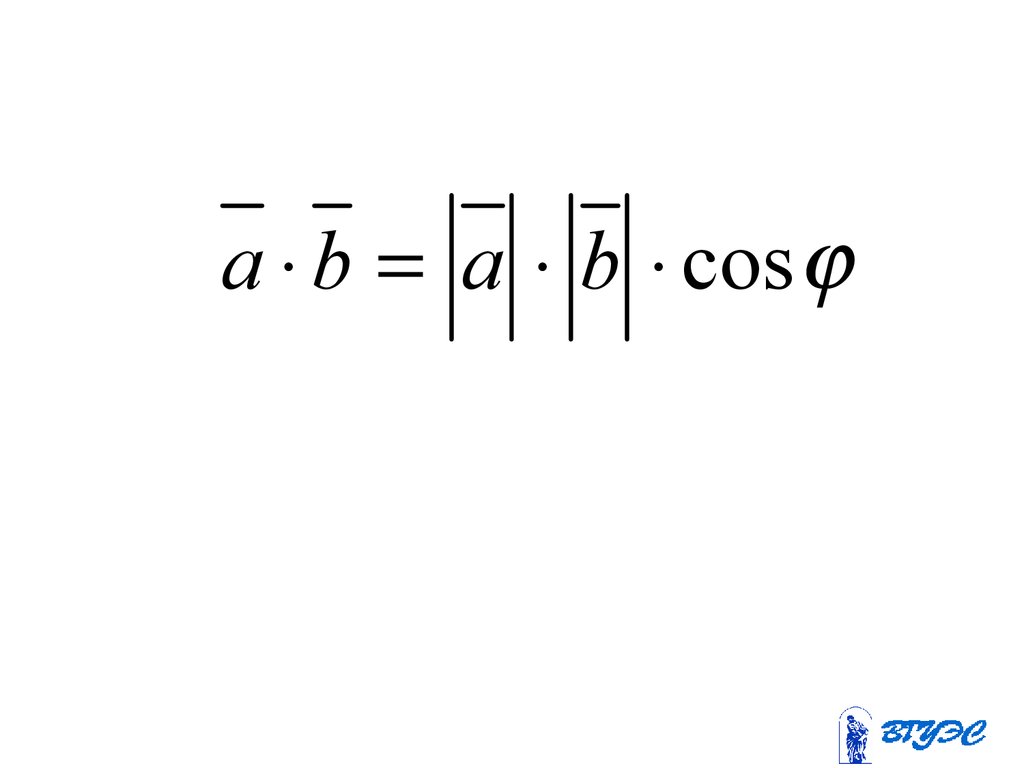

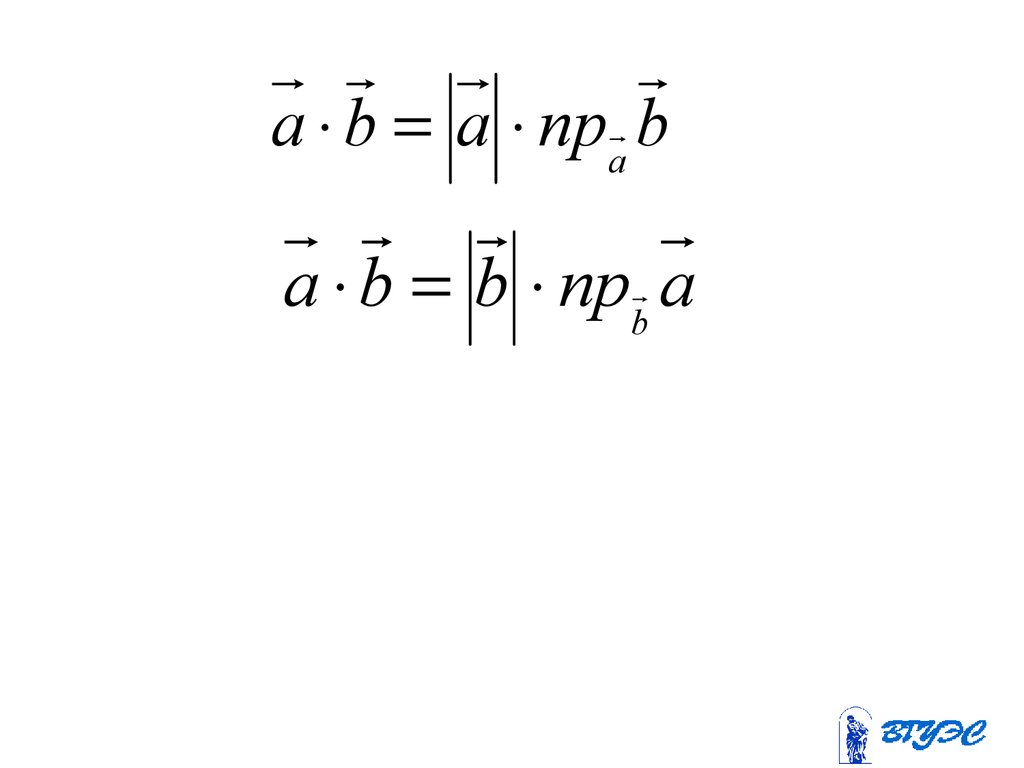





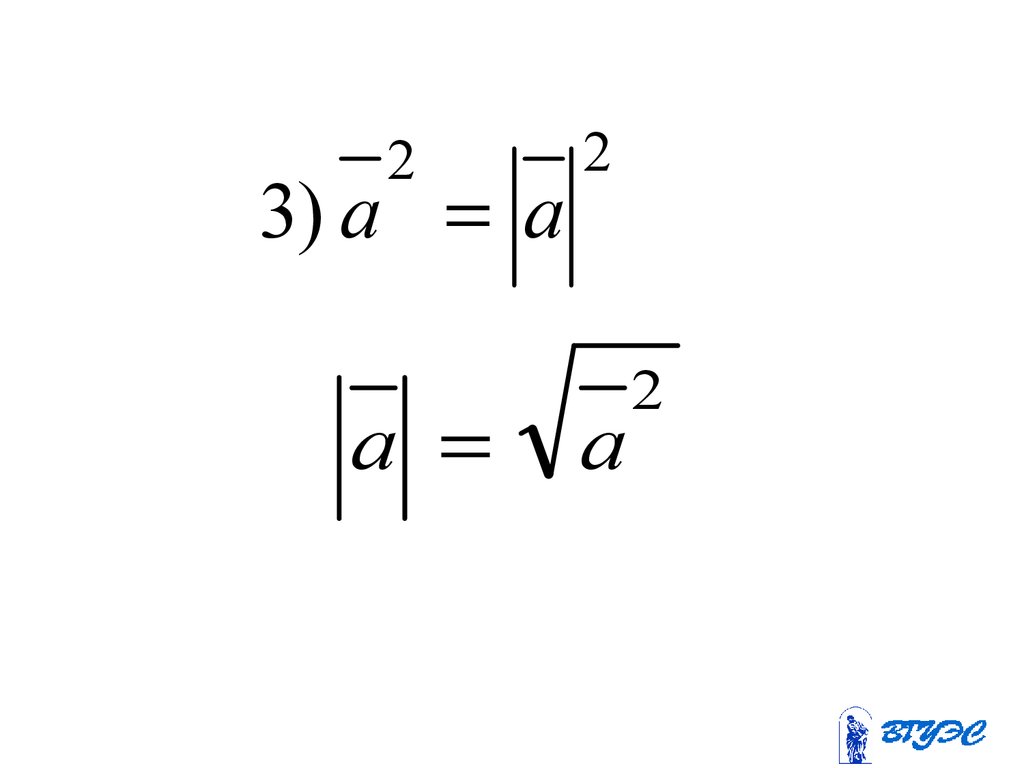



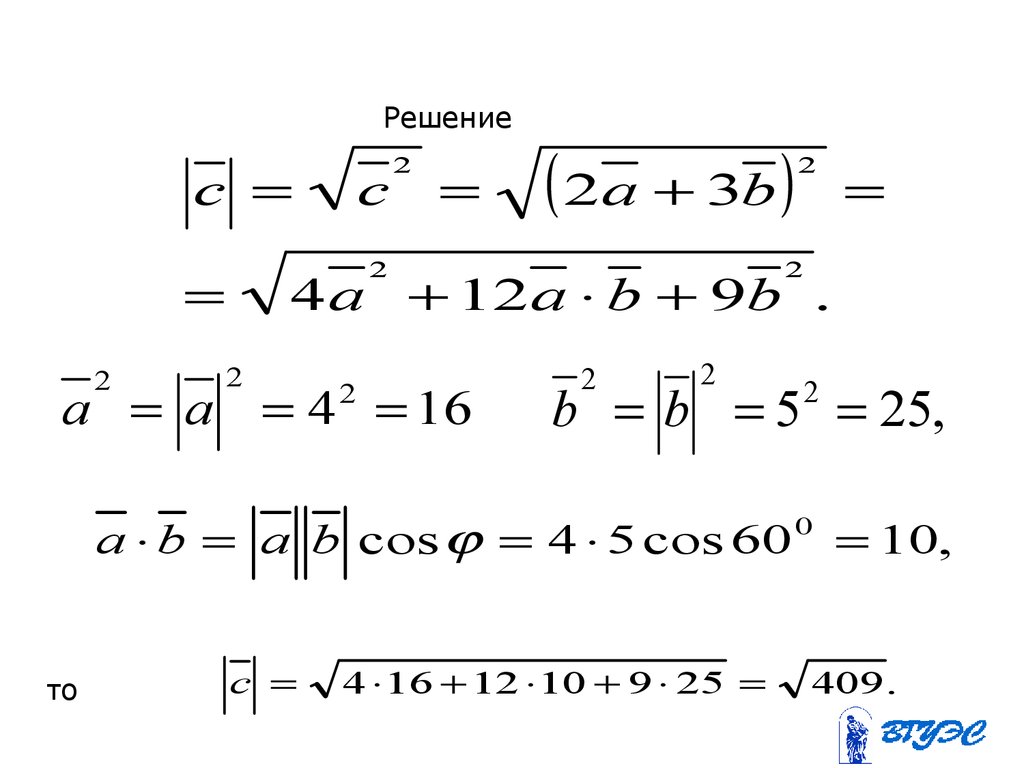







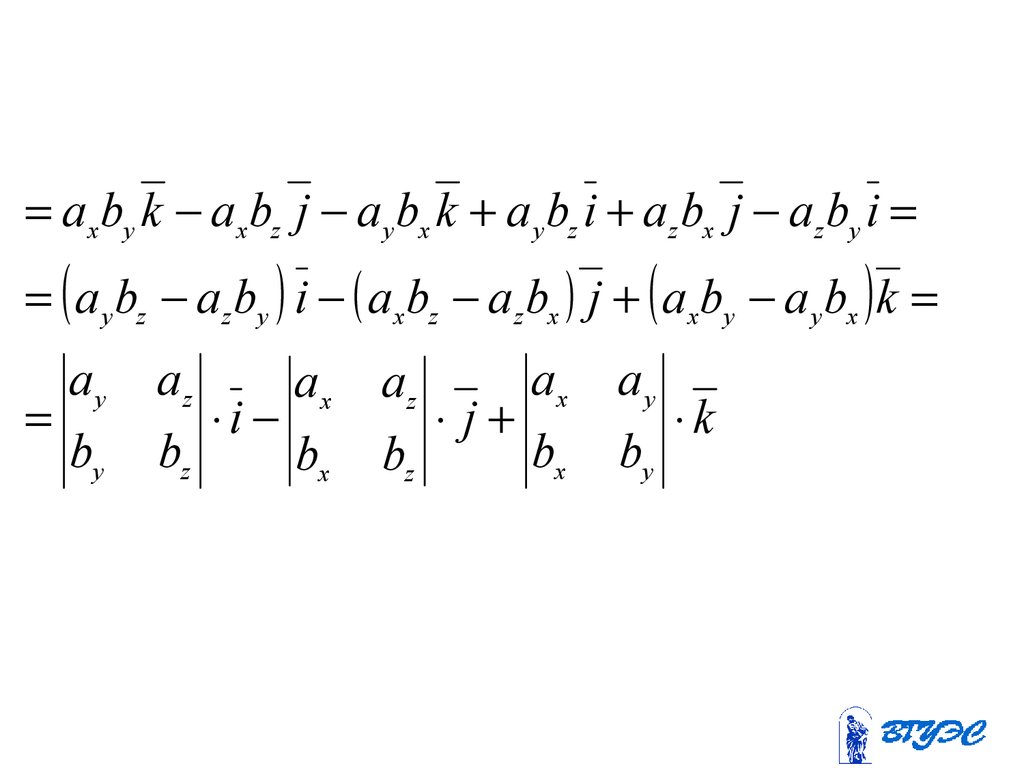


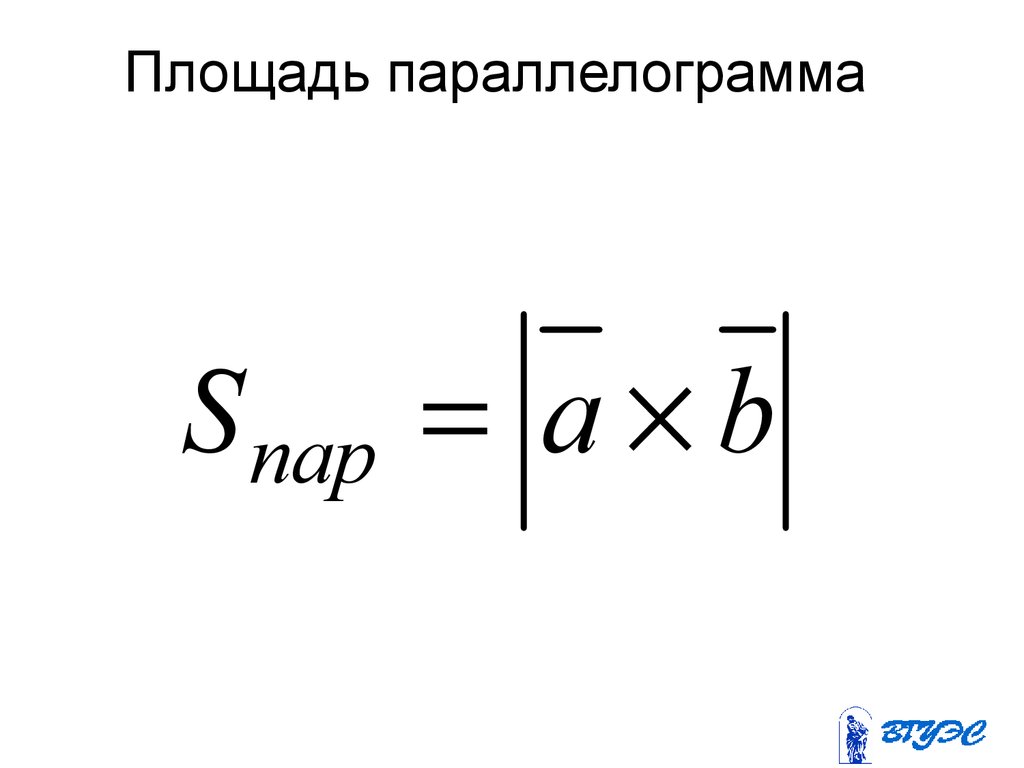



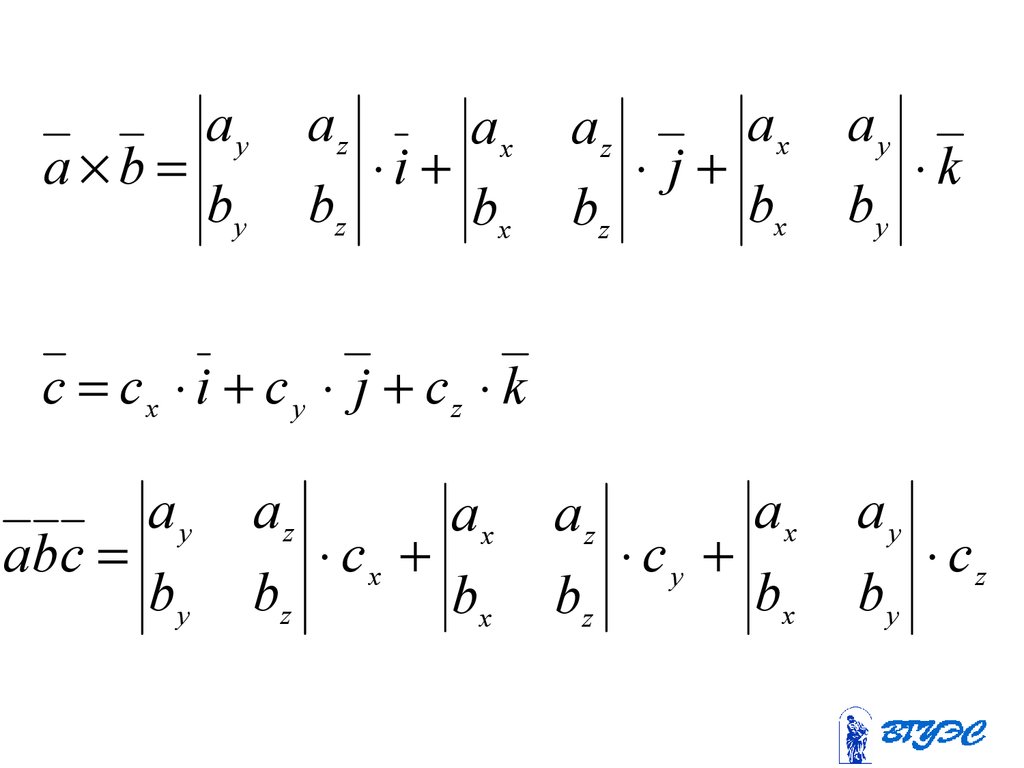

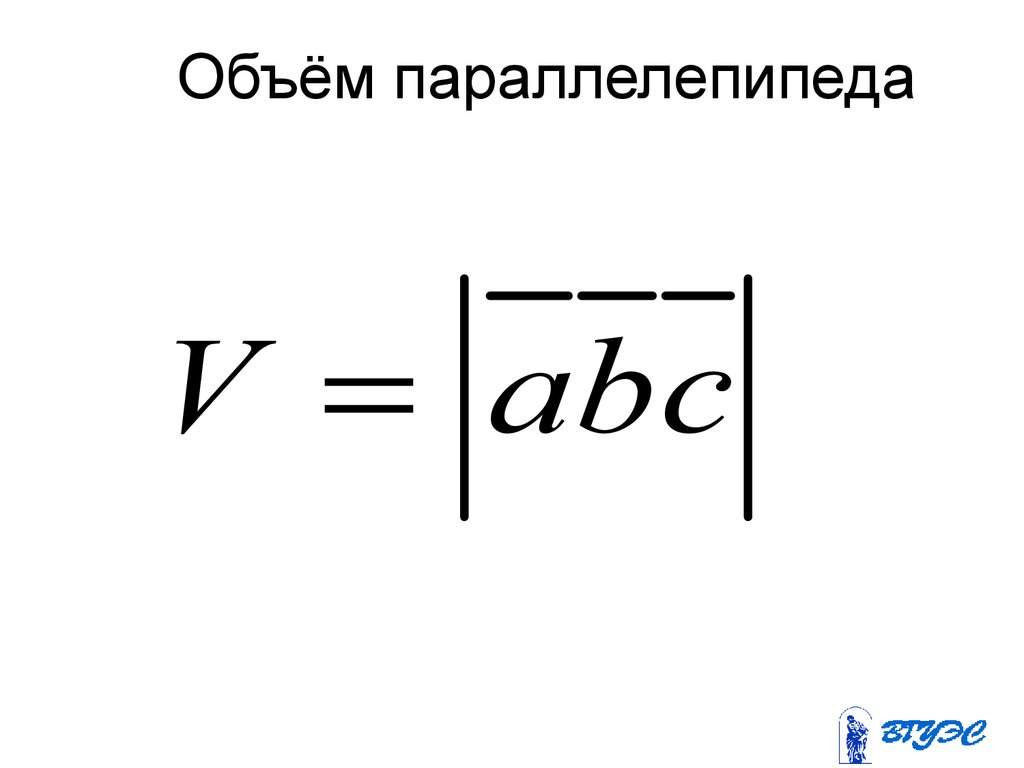

 Математика
Математика








