Закон сохранения энергии в механике

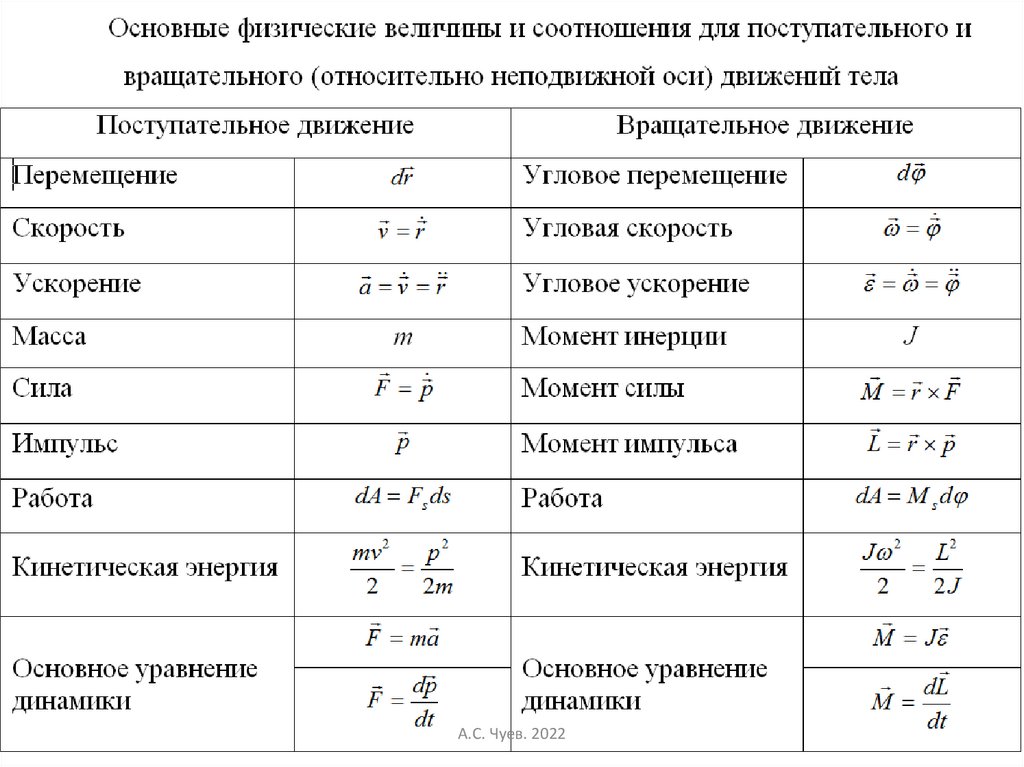
1.

Лекция 4. «Закон сохранения
энергии в механике»
Работа и кинетическая энергия
Консервативные силы
Работа в потенциальном поле
Потенциальная энергия тяготения и упругих
деформаций
• Связь между потенциальной энергией и силой
• Закон сохранения энергии
А.С. Чуев. 2022
1

2.

Нет ничего более упорядоченного, чем природа.
Мировой организм есть неразрывное целое.
Все элементы мироздания гармонично связаны
между собой.
Цицерон
А.С. Чуев. 2022
2

3.

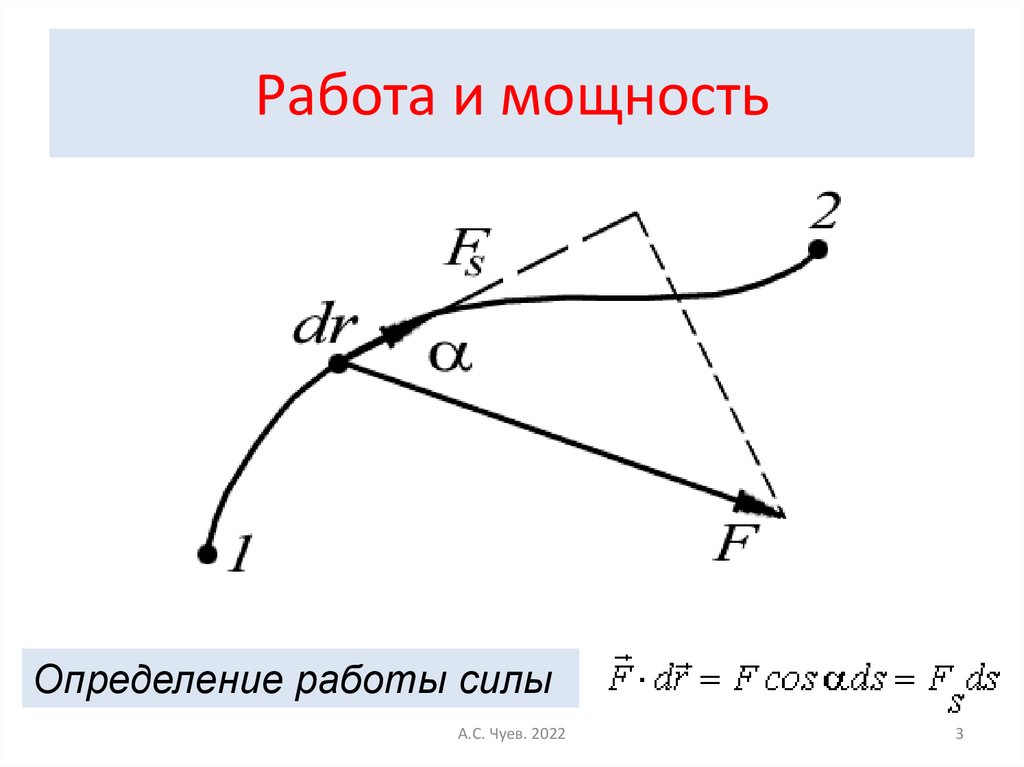
Работа и мощность
Определение работы силы
А.С. Чуев. 2022
3

4.

А.С. Чуев. 2022
4

5.

Элементарная работа силы
Интегральная работа силы
А.С. Чуев. 2022
5

6.

Для работы:
dim A ML T
2
кг м
[ A]
Дж
2
с
2
2
Мощность - это работа, совершаемая силой
(в механике) за единицу времени
Для мощности:
dim N ML T
2
3
А.С. Чуев. 2022
кг м
[N ]
Вт
3
с
2
6

7.

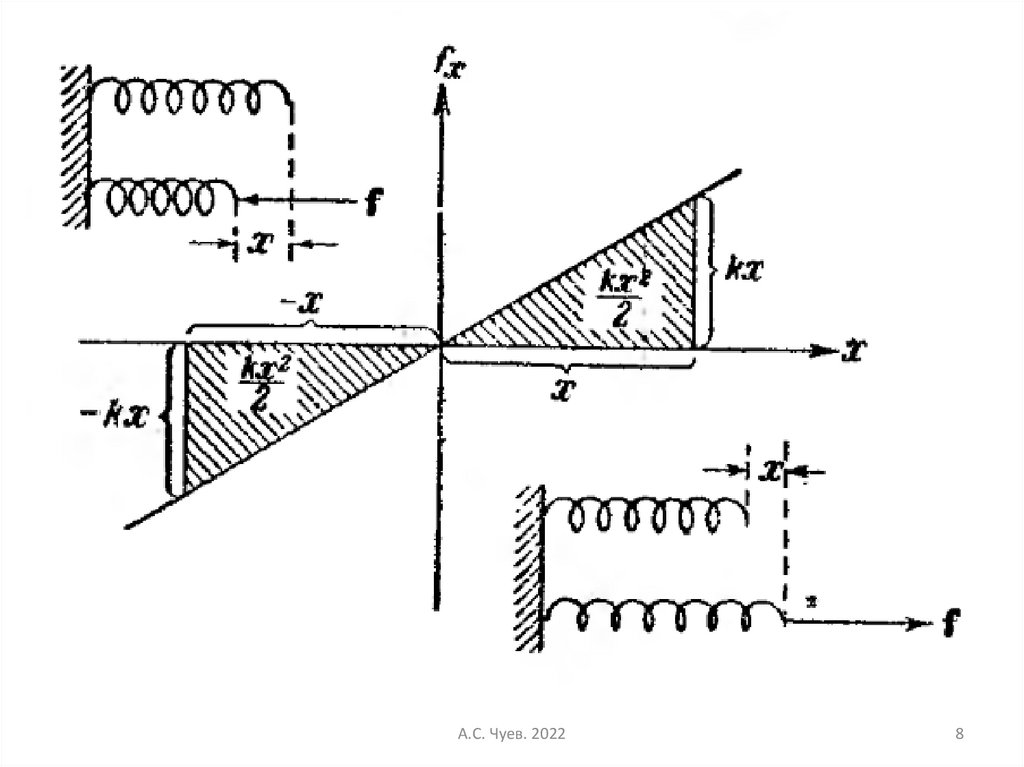
Потенциальная энергия и работа упругой
деформации (пружины)
Закон Гука. Сила упругости
F kx,
Сила непостоянна, поэтому элементарная работа
упр
dA Fdx kxdx
знак минус говорит о том, что работа
совершается против силы действия пружины.
kx kx
A dA kxdx
,
2
2
x2
2
2
1
2
x1
А.С. Чуев. 2022
7

8.

А.С. Чуев. 2022
8

9.

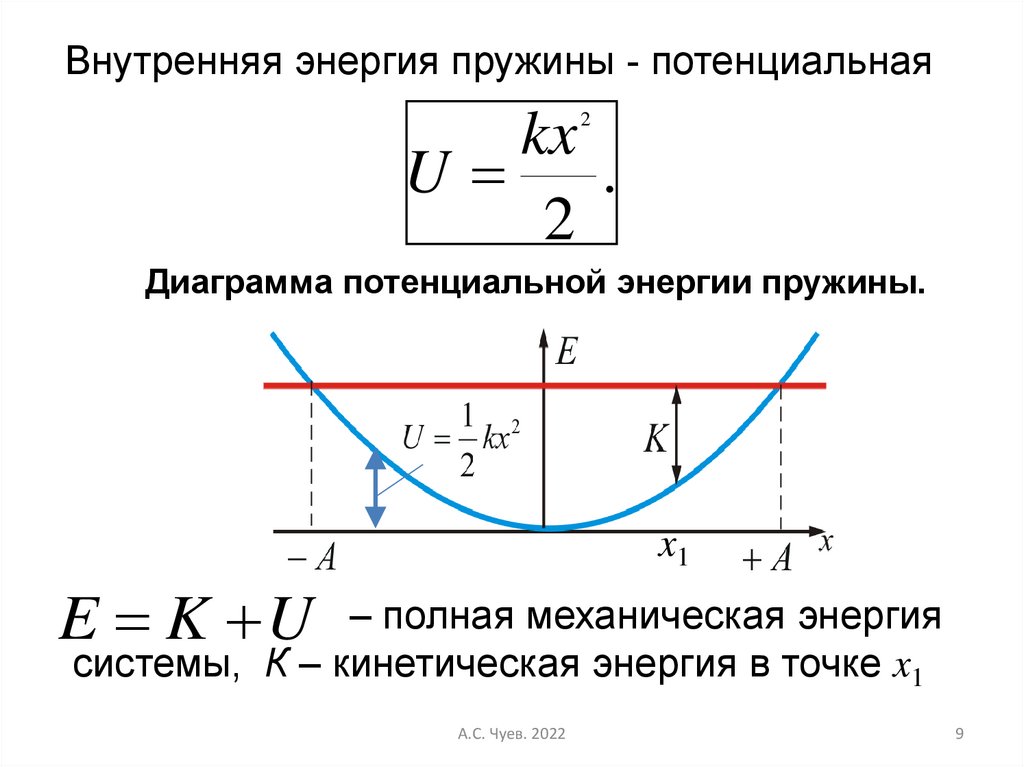
Внутренняя энергия пружины - потенциальная
kx
U
.
2
2
Диаграмма потенциальной энергии пружины.
x1
E K U
– полная механическая энергия
системы, К – кинетическая энергия в точке x1
А.С. Чуев. 2022
9

10.

Кинетической энергией поступательного
движения называется соотношение:
mv 2
K
.
2
К - является функцией состояния системы
(ФС не зависит от предыстории).
K – аддитивная величина:
2
i
mi v
K
,
2
i 1
n
А.С. Чуев. 2022
10

11.

Связь кинетической энергии с импульсом
Т.к.
mv 2 m m2 v 2
,
2 m 2m
2
p
отсюда K
2m
Связь кинетической энергии с работой
работа силы приложенной к телу на пути
r численно равна изменению
кинетической энергии этого тела:
A K
А.С. Чуев. 2022
11

12.

13.

А.С. Чуев. 2022
13

14.

Работа, энергия и мощность
при вращательном движении
dA Md
A M
I
L
K
2
2I
2
2
dA
N
M
dt
А.С. Чуев. 2022
14

15.

• Сила называется консервативной или
потенциальной, если её работа не
зависит от траектории, а определяется
только начальным и конечным
положениями тела. Работа таких сил по
перемещению тела по замкнутой
траектории всегда равна нулю. ... Если
работа силы зависит от траектории, то
такие силы называются неконсерватив
ными.
А.С. Чуев. 2022
15

16.

Работа консервативных сил
в потенциальном поле
A2'1 A21 mgh
А.С. Чуев. 2022
16

17.

Потенциальная энергия
Если
в
системе
материальных
тел
действуют консервативные силы, то можно
ввести понятие потенциальной энергии.
Работа,
совершаемая
консервативными
силами при изменении конфигурации системы, не
зависит от того, как было осуществлено это
изменение.
Работа
определяется
только
начальной и конечной конфигурациями системы:
А.С. Чуев. 2022
17

18.

A U U ,
12
1
2
(*)
здесь потенциальная энергия U (х, у, z) –
функция состояния системы, зависящая
только от координат всех тел системы в
поле консервативных сил.
Итак, K – определяется скоростью движения
тел системы, а U – их взаимным расположением.
Из (*) следует, что работа консервативных
сил равна убыли потенциальной энергии:
dA dU .
А.С. Чуев. 2022
18

19.

Работа силы тяжести
А.С. Чуев. 2022
19

20.

Потенциальная энергия при
гравитационном взаимодействии
Нет единого выражения для U. В разных
случаях она определяется по-разному.
Работа тела при падении
Или
A U U .
A mgh.
0
Удобно считать, что на поверхности
земли (h 0), U 0
тогда U A т.е.
0
А.С. Чуев. 2022
U mgh.
20

21.

Для случая гравитационного
взаимодействия между массами M и m,
находящимися на расстоянии r друг от
друга, потенциальную энергию определяют
по формуле:
Mm
U γ
.
r
W
M
ГР G
Потенциал гравитационного
m
4 r
поля:
F
M
Напряженность гравитационного поля: E ГР
G
m
4 r 2
G 4
EГР grad ГР
А.С. Чуев. 2022
21

22.

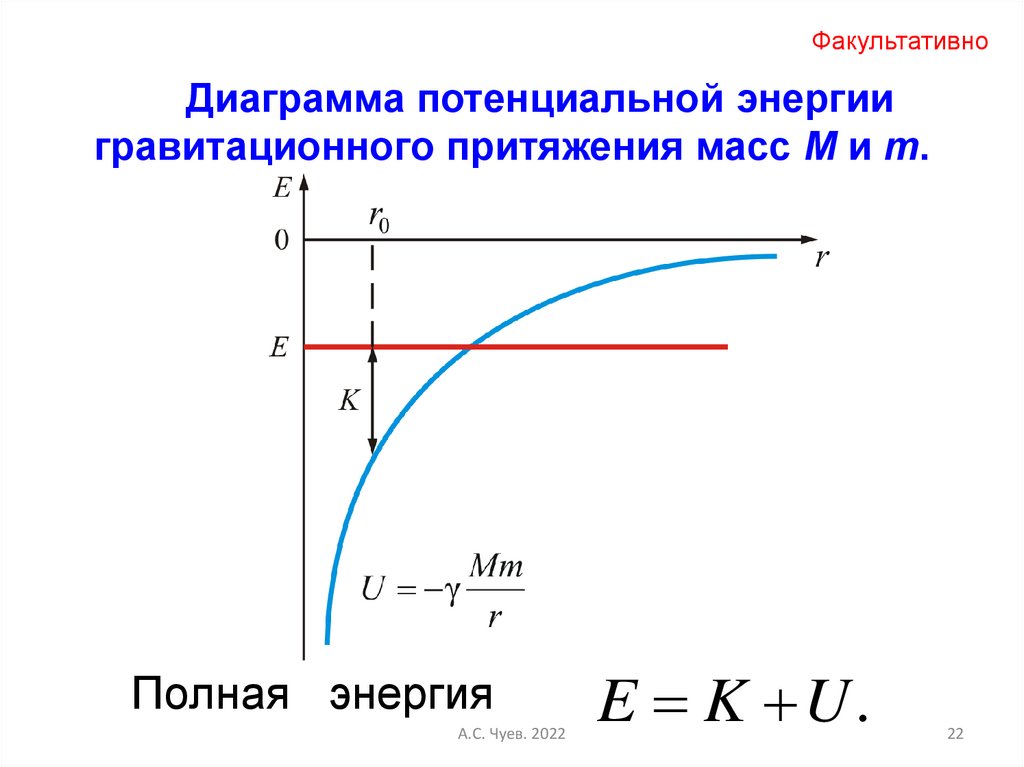
Факультативно
Диаграмма потенциальной энергии
гравитационного притяжения масс M и m.
Полная энергия
А.С. Чуев. 2022
E K U.
22

23.

Факультативно
Этим слагаемым можно пренебречь
А.С. Чуев. 2022
23

24.

Факультативно
Динамика орбитального движения планет
- кинетическая энергия
- потенциальная энергия
А.С. Чуев. 2022
24

25.

Факультативно
А.С. Чуев. 2022
25

26.

Факультативно
А.С. Чуев. 2022
26

27.

Факультативно
А.С. Чуев. 2022
27

28.

Факультативно
А.С. Чуев. 2022
28

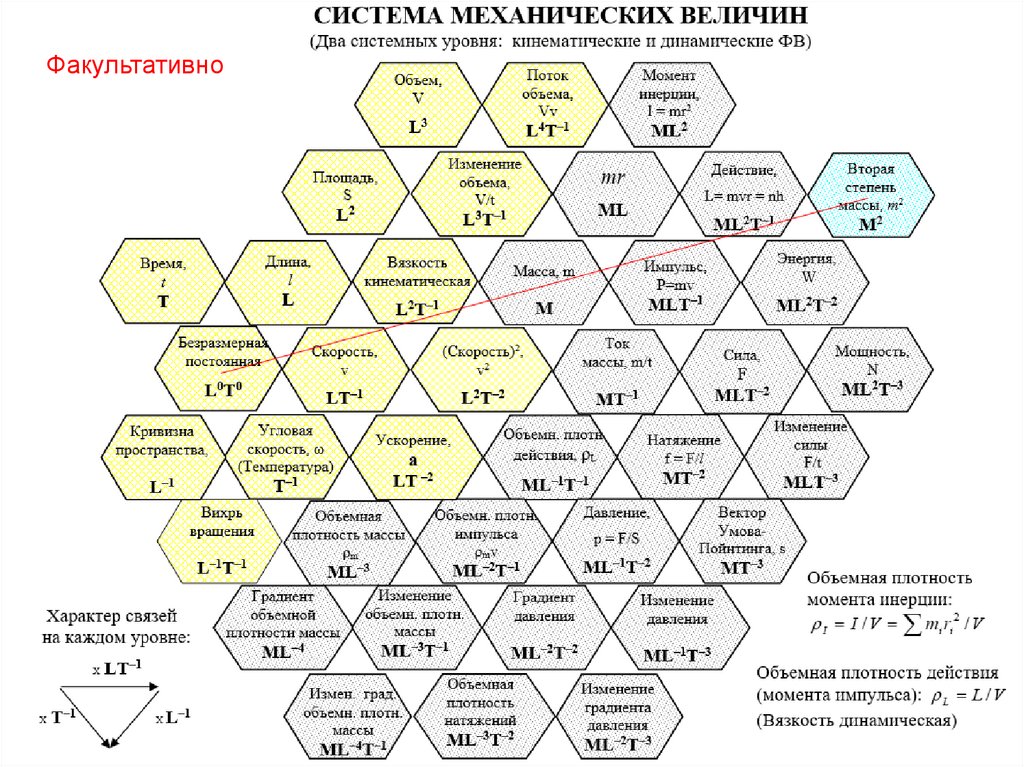
29.

Факультативно
А.С. Чуев. 2022
29

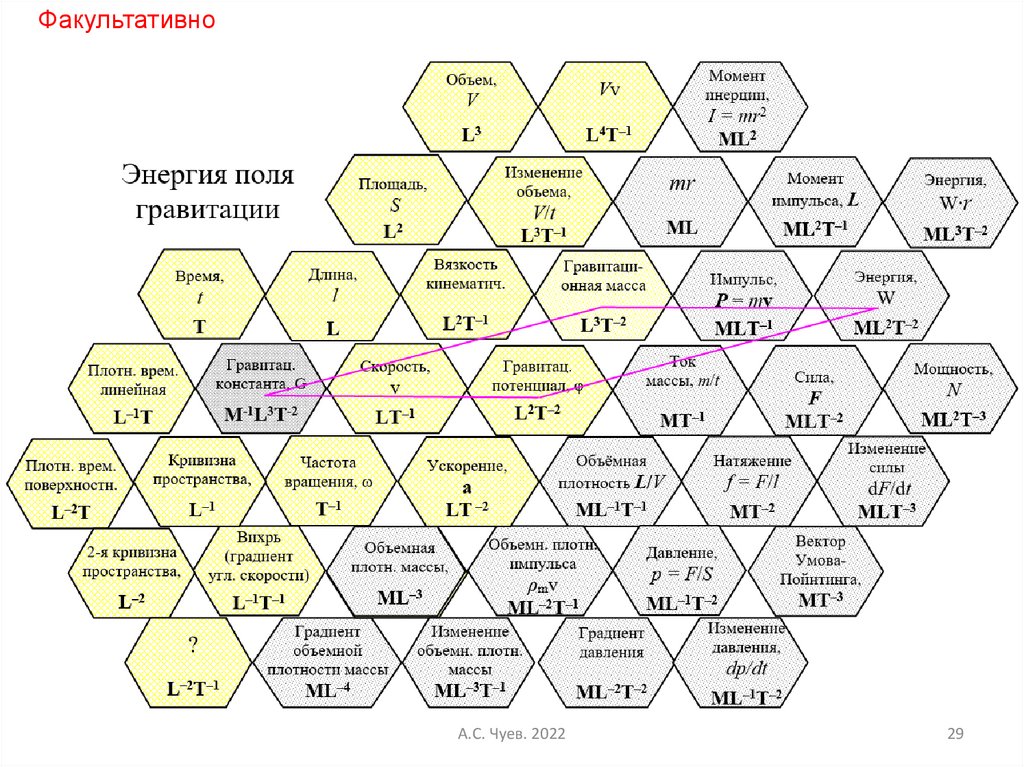
30.

Факультативно
А.С. Чуев. 2022
30

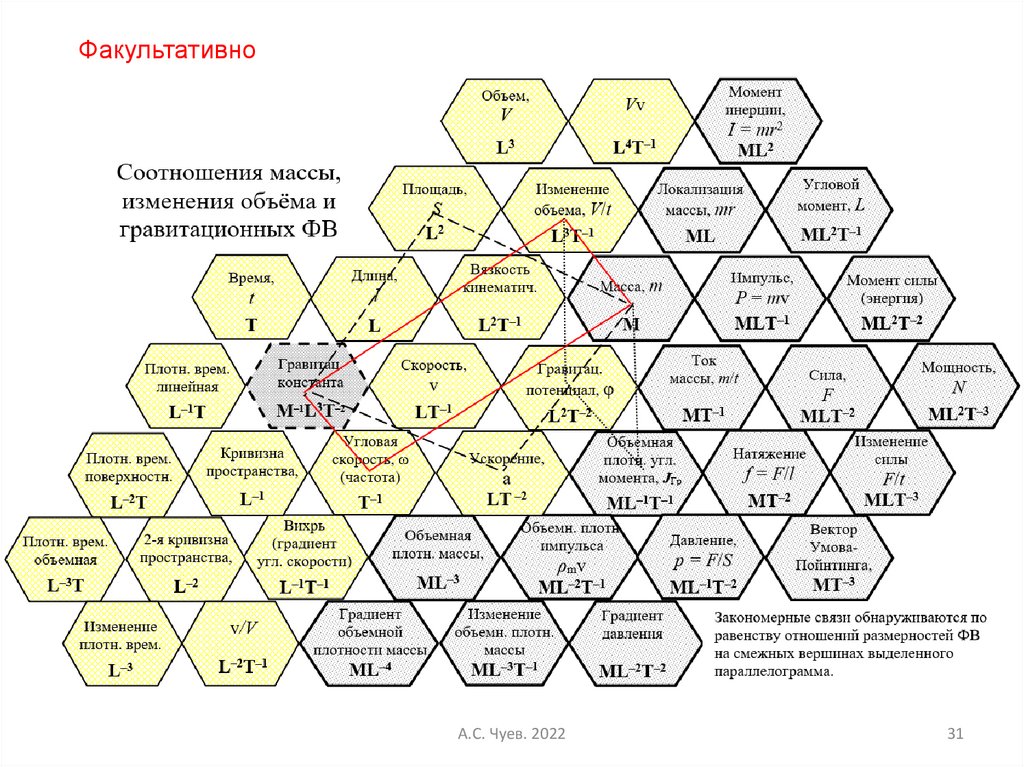
31.

Факультативно
А.С. Чуев. 2022
31

32.

ТЕОРЕМА О ВИРИАЛЕ
1
1
2
m v U
2
2
Средняя кинетическая энергия материальной
точки, совершающей пространственно
ограниченное движение под действием сил
притяжения, подчиняющихся закону обратных
квадратов, равна половине ее средней
потенциальной энергии с обратным знаком
А.С. Чуев. 2022
32

33.

Связь между потенциальной энергией и
силой
Пространство,
в
котором
действуют
консервативные
силы,
называется потенциальным полем.
Каждой точке потенциального поля
соответствует некоторое значение силы F
действующей на тело, и некоторое значение
потенциальной энергии U.
F
Между силой
и потенциальной
энергией U имеется связь.
А.С. Чуев. 2022
33

34.

dU
F
dr
Проекции вектора силы на оси координат:
U
Fx
;
x
U
Fy
;
y
А.С. Чуев. 2022
U
Fz
.
z
34

35.

Через проекции вектор силы записывается так:
U
U
U
F
i
j
k
y
z
x
или более коротко F gradU
i j k.
где grad
x y
z
А.С. Чуев. 2022
35

36.

Градиент
направление
функции.
– это вектор, показывающий
наибыстрейшего
увеличения
F gradU
В формуле стоит знак «минус», что означает
направленность силы в сторону наибыстрейшего
уменьшения U.
А.С. Чуев. 2022
36

37.

Закон сохранения механической
энергии
В сороковых годах девятнадцатого века
трудами Р. Майера, Г. Гельмгольца и Дж.
Джоуля (в разное время и независимо друг
от друга) был доказан закон сохранения и
превращения энергии.
А.С. Чуев. 2022
37

38.

Для консервативной системы частиц
полная энергия системы:
E K U
внутр.
U
внеш .
const
Для механической энергии закон сохранения
звучит так: полная механическая энергия
консервативной системы материальных
точек остаётся постоянной.
А.С. Чуев. 2022
38

39.

Для замкнутой системы,
т.е. для системы на которую не действуют
внешние силы, можно записать:
E K U
внутр.
const
т.е.
полная
механическая
энергия
замкнутой системы материальных точек,
между которыми действуют только
консервативные
силы,
остаётся
постоянной.
А.С. Чуев. 2022
39

40.

Если в замкнутой системе действуют
неконсервативные силы, то полная
механическая энергия системы не
сохраняется – частично она переходит в
другие виды энергии – неконсервативные.
Система, в которой механическая
энергия переходит в другие виды энергии,
называется диссипативной,
а сам процесс перехода называется
диссипацией энергии.
А.С. Чуев. 2022
40

41.

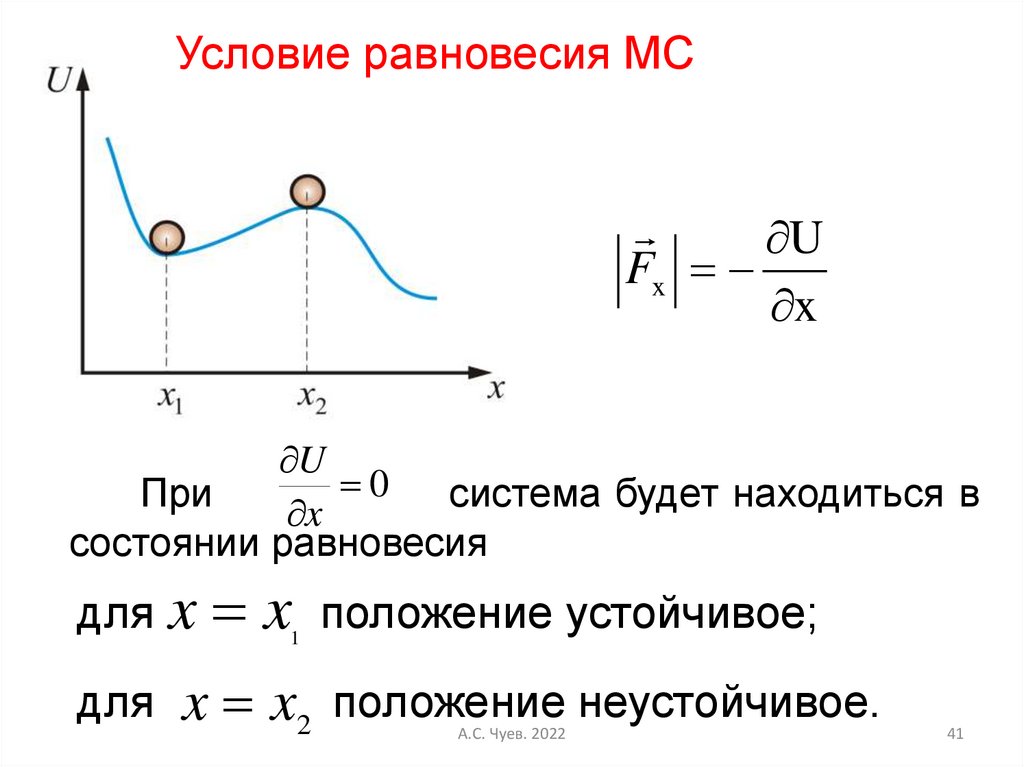
Условие равновесия МС
U
Fx
x
U
0
При
система будет находиться в
x
состоянии равновесия
для x
для
x
1
положение устойчивое;
x x2 положение неустойчивое.
А.С. Чуев. 2022
41

42.

Превращения энергии
А.С. Чуев. 2022
42

43.

А.С. Чуев. 2022
43

44.

А.С. Чуев. 2022
44

45.

А.С. Чуев. 2022
45

46.

Законы сохранения и причина их
действия по теореме Э. Нётер
Энергии
Однородность
времени
Импульса
Однородность
пространства
Момента импульса
Изотропность
пространства
Электрического заряда Симметрия П-В к
градиентным
преобразованиям
А.С. Чуев. 2022
46

47.

Факультативно
А.С. Чуев. 2022
47

48.

Факультативно
А.С. Чуев. 2022
48

49.

Конец лекции 4-2022
А.С. Чуев. 2022
49