Похожие презентации:
Законы сохранения в механике
1. Законы сохранения в механике
2. Замкнутая система
Замкнутой (изолированной) системой тел вмеханике называется система, на которую
не действуют внешние силы
3. Рассмотрим замкнутую систему двух тел массами m1 и m2
Скорости тел до взаимодействияи
Скорости тел после взаимодействия
и
4. По второму закону Ньютона
или:m1 1 m1 1 F12 t ,
m2 2 m2 2 F21 t ,
dp1 F12 dt
dp2 F21 dt
Сложив почленно эти равенства, получим:
d p1 p2 F12 F21 dt 0 ,
5. По третьему закону Ньютона
Полный импульс системы сохраняется6. Закон сохранения импульса
в замкнутой системе полныйимпульс сохраняется
7. Если на систему действуют внешние силы,
то полный импульс сохраняетсятолько в случае компенсации
данных внешних сил
8.
Даже если равнодействующая внешнихсил не равна нулю, но равна нулю её
проекция на какую-либо ось, то проекция
полного импульса системы на ту же ось
сохраняется
9. Механическая работа
A F S F S cosгде
– угол между
векторами силы и
перемещения.
При
>90 работа ΔA<0.
Единица измерения работы
в СИ – Джоуль
10. Если траектория движения тела – кривая линия и сила не постоянна,
то траекторию разбивают на малые участкикаждого из которых работа определяется
соотношением
, для
11. Полная работа на всей траектории
будет равна сумме работ на каждом изучастков:
A A
n
i 1
i
12.
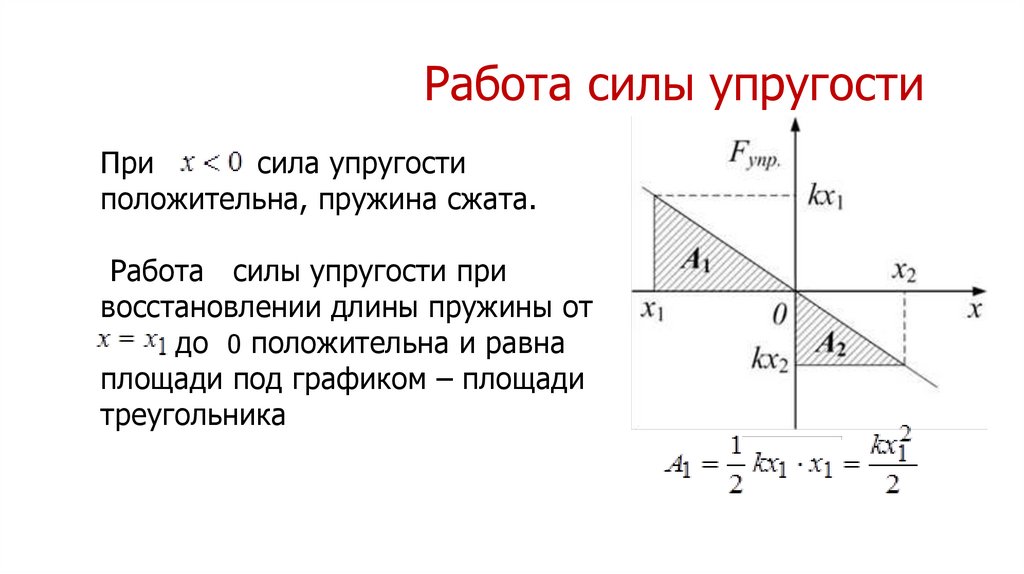
13. Работа силы упругости
Присила упругости
положительна, пружина сжата.
Работа силы упругости при
восстановлении длины пружины от
до 0 положительна и равна
площади под графиком – площади
треугольника
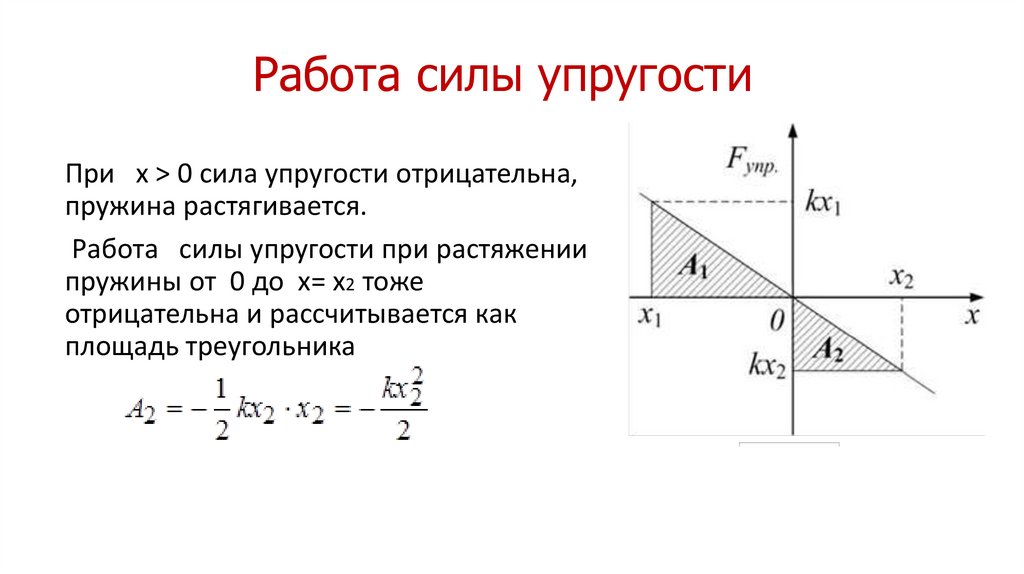
14. Работа силы упругости
При x > 0 сила упругости отрицательна,пружина растягивается.
Работа силы упругости при растяжении
пружины от 0 до x= x2 тоже
отрицательна и рассчитывается как
площадь треугольника
15. Суммарная работа силы упругости
kx kx k x xA A1 A2
2
2
2
2
1
2
2
2
1
2
2
Работа упругой силы не зависит от промежуточных
состояний, а зависит только от начального и конечного
состояния пружины.
Если начальная и конечная деформации равны, то работа
равна нулю. Такие силы называются консервативными.
16. Консервативная сила
сила, работа которой не зависит от формытраектории,
а
зависит
только
от
начального и конечного положения тела
Работа консервативной силы
замкнутой траектории равна нулю
по
любой
17. Сила трения
Сила трения не является консервативнойРабота силы трения всегда отрицательна, так
как сила всегда противоположна перемещению
Работа этой силы по замкнутой траектории
будет всегда отлична от нуля
Сила трения относится к диссипативным силам
18. Диссипативные силы
это силы, работа которых зависит не толькоот начального и конечного положения тела,
но и от формы траектории, а работа по
замкнутой траектории не равна нулю
19. Мощность
- быстрота совершения работы (Вт)Средняя мощность – работа за единицу
времени:
A
Р
t
20. Мгновенная мощность
dAP
dt
dA P dt
2
t2
1
t1
A12 dA P dt
21. Если сила постоянна, то:
dA F dSdS
P
F
F
dt
dt
dt
22. Энергия
• кинетическая: энергия, которой обладаеттело вследствие движения;
• потенциальная: энергия, которой
обладает тело вследствие взаимодействия
с другими телами
23. Кинетическая энергия
mE кин
2
2
Теорема о кинетической энергии:
изменение кинетической энергии тела равно работе силы
(или равнодействующей всех сил, если сил несколько):
Eкин Eкин 2 Eкин1 A
24. Потенциальная энергия тела в поле силы тяжести Земли
E p. mghЭта формула справедлива только для
однородного поля тяготения:
g=const , то есть при h<< R Земли.
В зависимости от выбора начала
отсчёта потенциальная энергия
может быть как положительной, так и
отрицательной.
25. Если h<< R не соблюдается, то
Если h<< R не соблюдается, тоM m
E p.
r
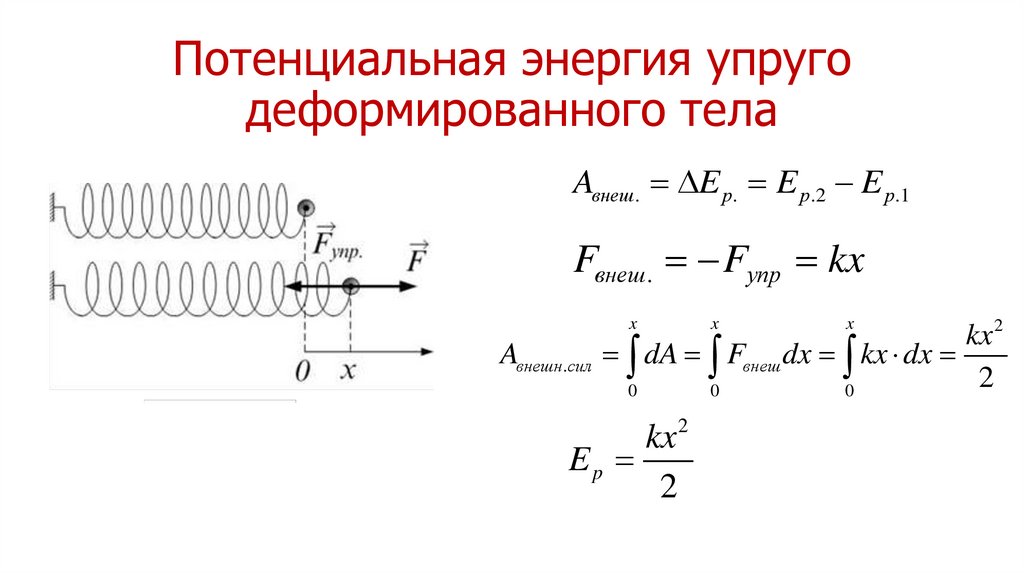
26. Потенциальная энергия упруго деформированного тела
Aвнеш. E p. E p.2 E p.1Fвнеш. Fупр kx
x
Aвнешн.сил
x
x
kx 2
dA Fвнеш dx kx dx
2
0
0
0
kx
Ep
2
2
27. Закон сохранения механической энергии
полная механическая энергия замкнутойсистемы, в которой действуют только
консервативные силы, остаётся постоянной:
Eмех. E p Eк const
Eмех1 Eмех 2
E p1 Eк1 E p 2 Eк 2
28.
При наличии диссипативных сил (силы трения,вязкости, силы неупругой деформации) механическая
энергия необратимо превращается в другие виды
энергии, например, тепловую.
Причём работа системы против диссипативных сил всегда
положительна.
E1мех E2 мех Aпротив
диссипативных сил
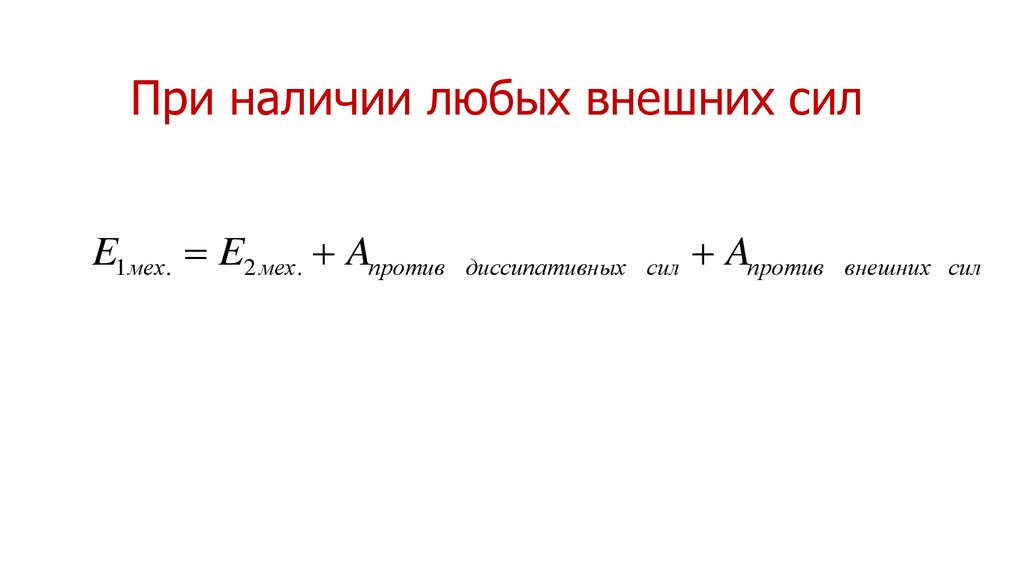
29. При наличии любых внешних сил
E1мех. E2 мех. Aпротивдиссипативных сил
Aпротив
внешних сил
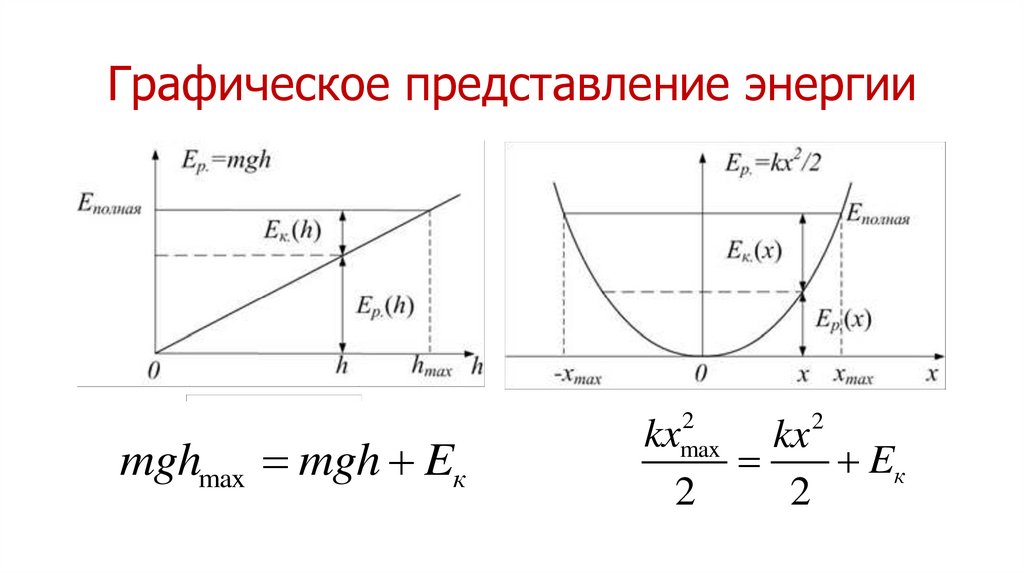
30. Графическое представление энергии
mghmax mgh Eк2
max
kx
2
2
kx
Eк
2


























 Физика
Физика Механика
Механика








