Работа и энергия. Закон сохранения энергии в механике

1. Работа и энергия. Закон сохранения энергии в механике

1. Механическая работа
2. Мощность
3. Энергия. Механическая энергия.
Кинетическая и потенциальная
энергия
4. Закон сохранения энергии в
механике

2.

Механическая работа
Механическая работа – скалярная физическая величина,
характеризующая движение тела под действием силы и равная
скалярному произведению вектора силы на вектор перемещения.
Элементарная работа:
dA F dr ,
А 1Н м 1 Дж
Знак работы:
π
0 α , dA 0
2
, dA 0
dA Fdr cos FS ds
dA Fx dx Fy dy Fz dz
dA F dt dp mvdv
2
π
α , dA 0
2
Работа при перемещении 1-2 :
2
2
2
1
1
1
A dA FS ds FS υdt
Работа численно равна площади под графиком
проекции силы на направление перемещения:
На основе III закона
Ньютона работа
силы и работа против силы противоположны
по знаку:
F F
dA dA
1, 2
2 ,1
1
2

3.

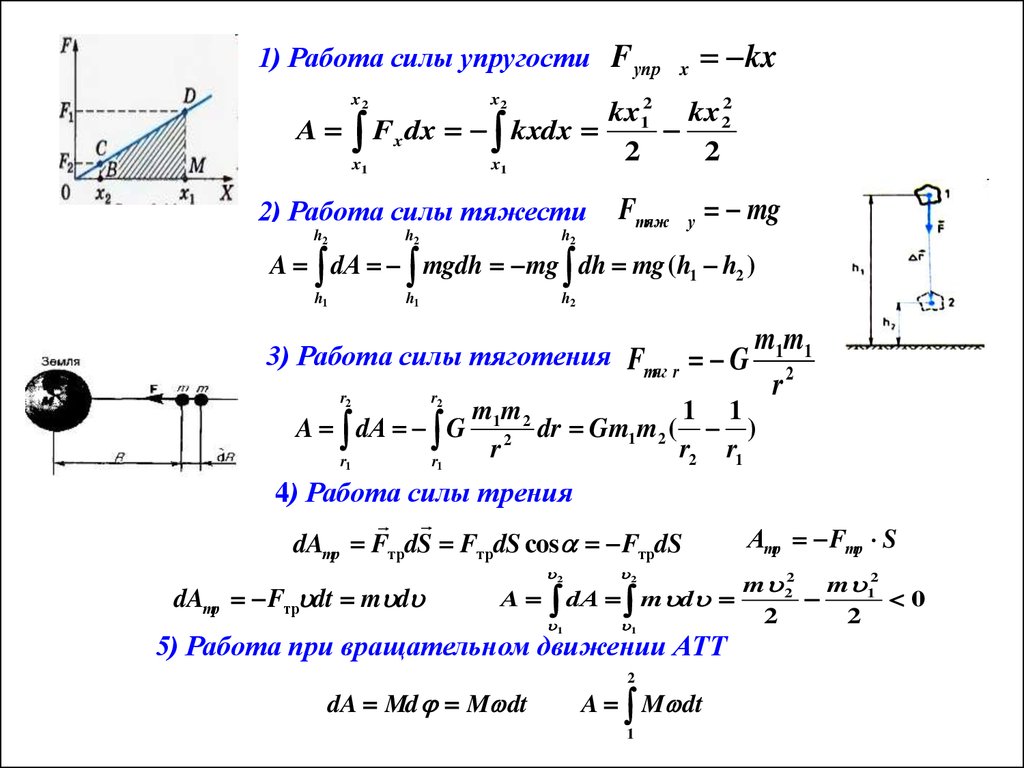
1) Работа силы упругости Fупр
x2
x
kx
x2
kx12 kx 22
A Fx dx kxdx
2
2
x1
x1
2) Работа силы тяжести
h2
h2
h2
h1
h1
h2
Fтяж
у
mg
A dΑ mgdh mg dh mg ( h1 h2 )
3) Работа силы тяготения Fтяг r G
r2
r2
r1
r1
A dΑ G
m1m1
r2
m1m 2
1 1
dr
Gm
m
(
)
1 2
2
r
r2 r1
4) Работа силы трения
dAтр FтрdS FтрdS cos FтрdS
dAтр Fтр dt m d
2
2
Атр Fтр S
m 22 m 12
A dΑ m d
0
2
2
1
1
5) Работа при вращательном движении АТТ
dA Md M dt
2
A M dt
1

4. Мощность

Мощность - скалярная физическая величина,
характеризующая быстроту совершения работы и равная
работе, совершаемой за единицу времени.
Средняя мощность определяется отношением работы ко времени, за
которое она была совершена:
N cp
A
F Vср ,
t
N 1 Дж 1Вт
1с
Мгновенная мощность равна производной от величины работы по времени:
dA d ( F r ) F dr
N
F V F V cos α ,
dt
dt
dt
F const
При известной мощности работа определяется выражениями:
A N ср t , dA N dt ,
A Ndt
s

5. Энергия

Энергия – скалярная физическая величина, являющаяся единой мерой
различных форм движения материи и характеризующая их способность к
взаимному превращению.
Энергия – конечная, однозначная, непрерывная, аддитивная
функция параметров состояния системы.
Формам движения материи соответствуют виды энергии:
Механическая
Внутренняя (тепловая)
Электромагнитная
Ядерная….
Закон сохранения энергии: в замкнутой системе тел энергия может
переходить от одних тел к другим, превращаться из одних видов в другие,
но её суммарное значение остаётся неизменным.

6. Механическая энергия

Механическая энергия – скалярная физическая величина,
мера механического движения тела, изменение которой
определяется работой действующих на тело сил.
Механическая энергия (W) - функция параметров
механического состояния: r ,V или r , p
W f ( r ,V ) f ( r , р )
W f ( x , y , z , p x , p y , pz )
Различают: кинетическую, обусловленную движением, и
потенциальную, связанную с взаимодействием,
составляющие механической энергии.
W Wкин Wпот

7. Кинетическая энергия

Кинетическая энергия, Wкин (V),- часть механической энергии,
обусловленная движением тела и зависящая от его
скорости (импульса).
Особенности кинетической энергии:
положительность, аддитивность, относительность.
Теорема об изменении кинетической энергии:
Изменение кинетической энергии тела равно работе
равнодействующей всех сил, приложенных к телу.
Aр всех сил
2
dv
m 22 m 12
F p dr m v dt m d
Wкин 2 Wкин 1 Wкин
dt
2
2
1
Поступательное движение
Wкин
m 2
p2
2
2m
Вращательное движение
Wкин
J 2
L2
2
2J

8. Потенциальная энергия

Потенциальная энергия, Wпот (r), – часть механической
энергии, обусловленная взаимодействием тел или их частей
и зависящая от положения тела в пространстве.
Особенности потенциальной энергии:
-может быть как положительна, так и отрицательна,
-её численное значение зависит от выбора нулевого уровня,
- расчётная формула определяется характером
взаимодействия.

9. Потенциальная энергия тела

1.Потенциальная энергия при действии силы упругости
Aупр
kx12 kx22
Wпот1 Wпот 2 Wпот
2
2
Wпот
kx 2
, W 0 при х 0
2
2. Потенциальная энергия тела в поле силы тяжести
Aтяж mgh1 mgh2 W пот1 Wпот 2 ΔWпот
Wпот mgh,
Wпот 0 при h 0
3.Потенциальная энергия тела в поле гравитации (силы тяготения)
Aтяг
Mm
Mm
G
G
Wпот 1 Wпот 2 Wпот
r2
r1
Wпот G
Mm
, Wпот 0
r
при r

10. Изменение потенциальной энергии

Потенциальную энергию тела обуславливает потенциальное поле сил, зависящих
от положения в нём тела : гравитационное поле, электростатическое поле, поле
упругих сил, поле сил тяжести…
С потенциальным
полем связаны консервативные силы, зависящие от положения
тел, F( x , y , z ) F( r ) , работа которых не зависит от формы траектории, а определяется
лишь начальным и конечным положением тела в потенциальном поле.
Работа консервативной силы при перемещения тела по замкнутой траектории
равна нулю.
A12
конс
2
2
2
1a
1b
1c
dAконс dAконс dAконс
Aконс dAконс 0
1 2 1
Консервативные силы: тяжести, тяготения, упругости, электростатические силы...
Работа консервативной силы равна убыли потенциальной энергии.
r2
Aконс
dAконс dWпот
Fdr Wпот(r 1 ) Wпот(r 2 ) Wпот 1 Wпот 2 Wпот
r1

11. Связь консервативной силы с потенциальной энергией

Выразим работу потенциальной силы через убыль потенциальной энергии:
dA Fx dx Fy dy Fz dz dWпот
Полный дифференциал функции трёх переменных dWx,y,z :
Wпот
Wпот
Wпот
dx
dy
dz
x
y
z
( x , y ,z )
Видим, что проекции вектора силы на координатные оси равны соответствующим
dWпот
частным производным от потенциальной энергии тела с противоположным знаком:
dWпот
Wпот
Wпот
Fz
Fy
dz
x
y
Wпот Wпот Wпот
F (
i
j
k)
F
x
y
z
Fx
Вектор силы
i
j
k
x
y
z
оператор
Wпот
градиента
Градиент функции– вектор, характеризующий быстроту изменения функции в
пространстве. Он направлен в сторону наиболее быстрого возрастания функции.
Действующая на тело в потенциальном поле сила равна по модулю и
противоположна по направлению градиенту потенциальной энергии тела.

12. Закон сохранения энергии в механике

Изменение механической энергии системы тел определяется работой
внутренних и внешних сил (консервативных, неконсервативных).
W Wкин Wпот
dWкин dAр dАконс dAнеконс dAвнеш
dWпот dAконс
d (Wкин Wпот ) dAнеконс dAвнеш
dW dAнеконс dAвнеш
Изменение полной механической энергии системы равно алгебраической
сумме работ всех неконсервативных и внешних сил, действующих на тела
системы.
Закон сохранения энергии в механике: полная механическая
энергия замкнутой консервативной системы тел есть
величина постоянная.
dAнеконс 0; dAвнеш 0
dW 0
W const
Wкин Wпот const

13. Закон сохранения механической энергии

Пример 1. Свободное падение- движение под действием силы тяжести при отсутствии
сил сопротивления
mυ 2
mgh
const
2
mv 32
mυ22
mgh1 mgh2
2
2
Пример 2. Абсолютно упругий удар- удар, при котором сохраняется механическая
энергия системы:
Закон сохранения энергии
2
2
mυ01
mυ02
mυ12
mυ22
2
2
2
2
Закон сохранения импульса
mυ01 mυ02 mυ1 mυ2

14. Закон сохранения механической энергии

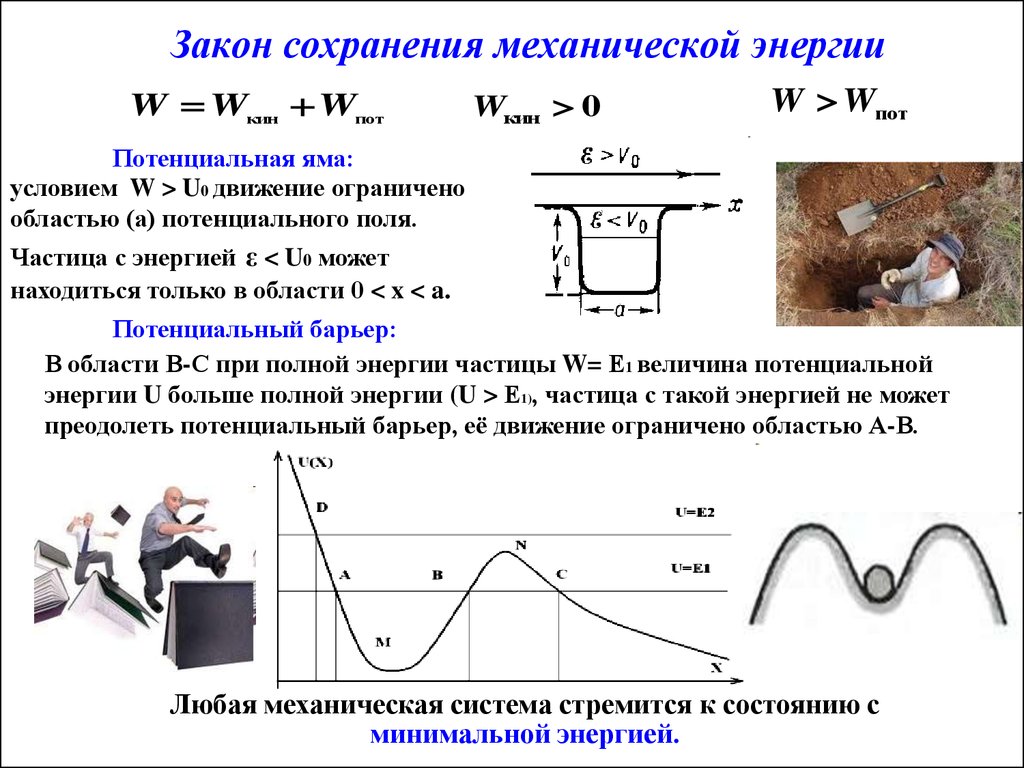
W Wкин Wпот
Wкин 0
W Wпот
Потенциальная яма:
условием W > U0 движение ограничено
областью (а) потенциального поля.
Частица с энергией ε < U0 может
находиться только в области 0 < x < a.
Потенциальный барьер:
В области В-С при полной энергии частицы W= Е1 величина потенциальной
энергии U больше полной энергии (U > Е1), частица с такой энергией не может
преодолеть потенциальный барьер, её движение ограничено областью А-В.
Любая механическая система стремится к состоянию с
минимальной энергией.

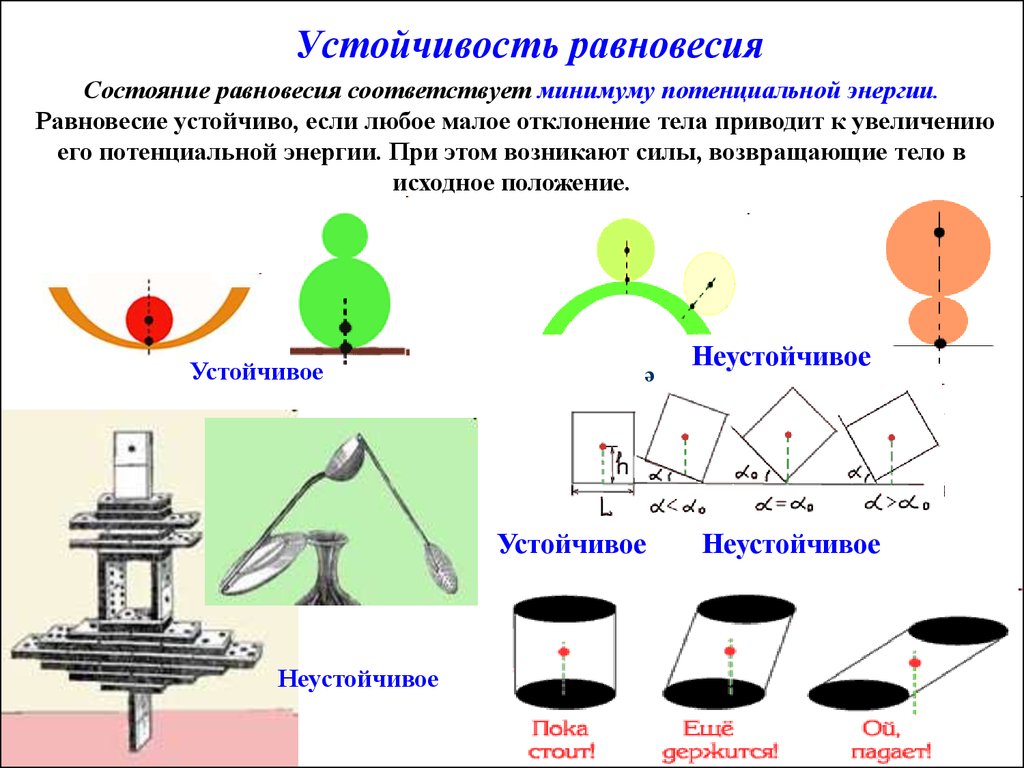
15. Устойчивость равновесия

Состояние равновесия соответствует минимуму потенциальной энергии.
Равновесие устойчиво, если любое малое отклонение тела приводит к увеличению
его потенциальной энергии. При этом возникают силы, возвращающие тело в
исходное положение.
е
Устойчивое
Устойчивое
Неустойчивое
Неустойчивое
Неустойчивое

16. Особенности классической механики

- Всеобщность законов движения в природе
- Задание начальных условий и законов
движения однозначно определяет все
последующие состояния. Вселенная- гигантский
детерминированный механизм.
- Движение обратимо
- Принцип дальнодействия
- Механицизм и редукционизм
- Корпускулярная модель реальности
- Абсолютность свойств пространства и
времени. Их независимость
- Основа технической революции