Похожие презентации:
Степенная функция (занятия 1, 2, 3)
1.
Как алгебраисты вместо АА, ААА, … пишут А2, А3, …так я вместо 1 , 12 , 13 пишу а-1, а-2, а-3, …
а
а
а
Ньютон И.
1 занятие
2.
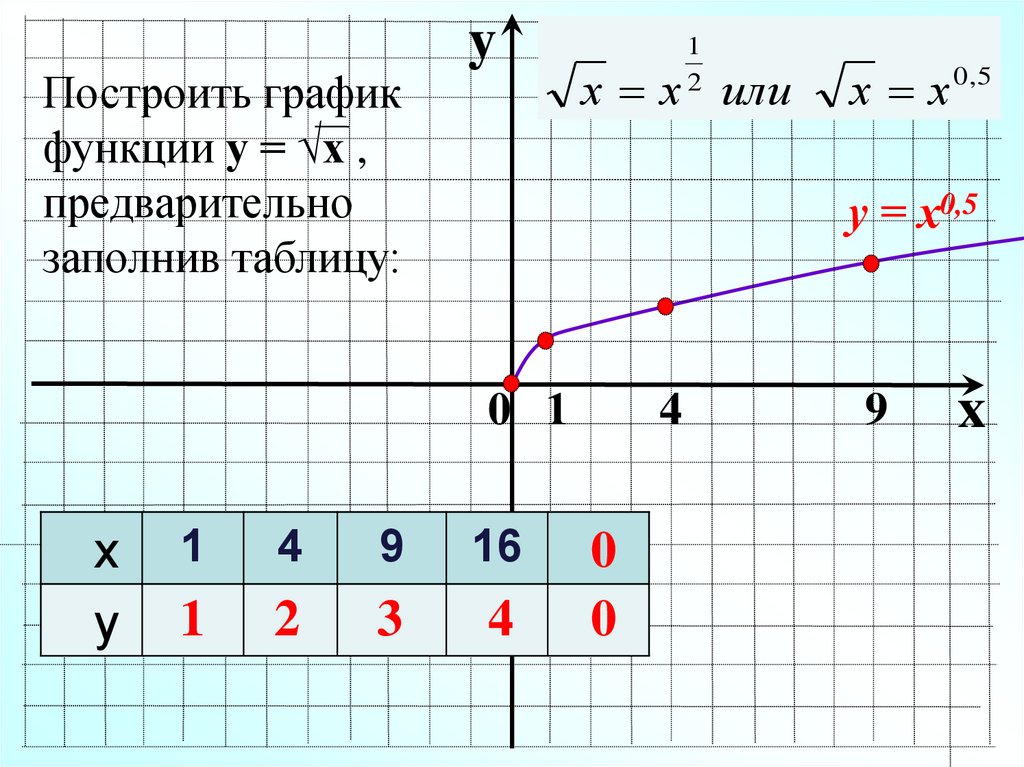
Построить графикфункции у = √х ,
предварительно
заполнив таблицу:
y
1
2
х х или
у = х0,5
0 1
х
у
х х 0,5
1
4
9
16
1
2
3
4
4
0
0
9
x
3.
Степенной функцией называетсяфункция вида у = хр,
где р – заданное действительное число
Замечание. Все графики функций, изображённые
на слайдах, строим в тетради.
4.
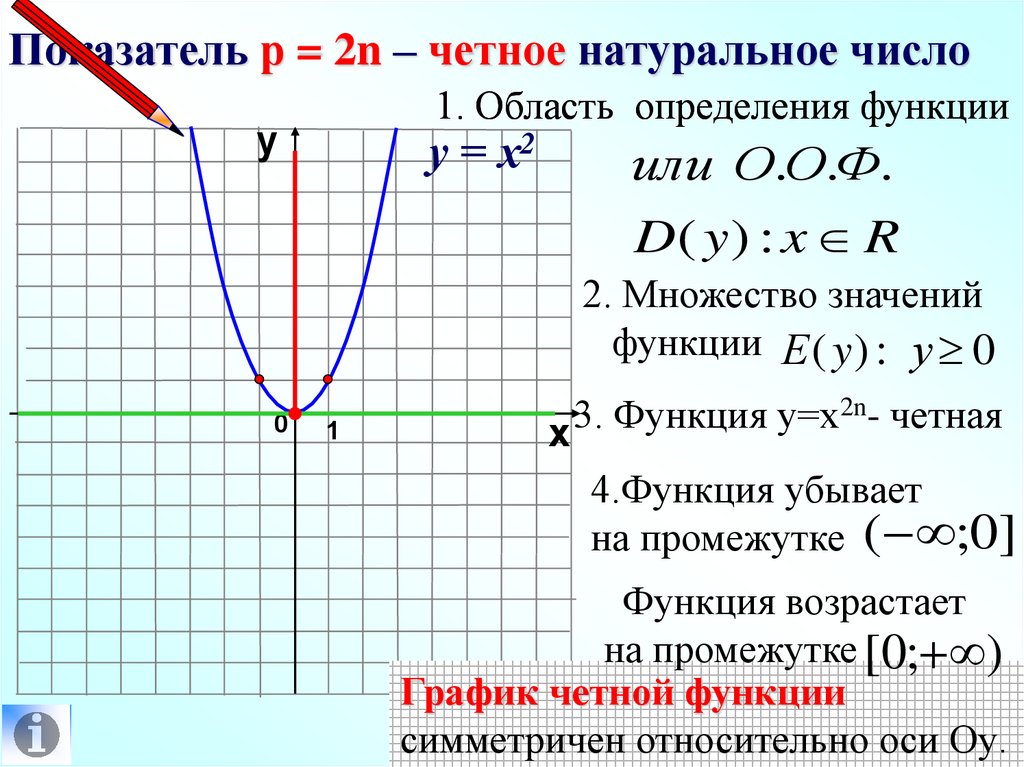
Показатель р = 2n – четное натуральное число1. Область определения функции
у
у = х2
или О.О.Ф.
D( y ) : x R
2. Множество значений
функции Е ( y ) : у 0
0
1
2n- четная
3.
Функция
у=х
х
4.Функция убывает
на промежутке ( ;0]
Функция возрастает
на промежутке [0; )
График четной функции
симметричен относительно оси Оу.
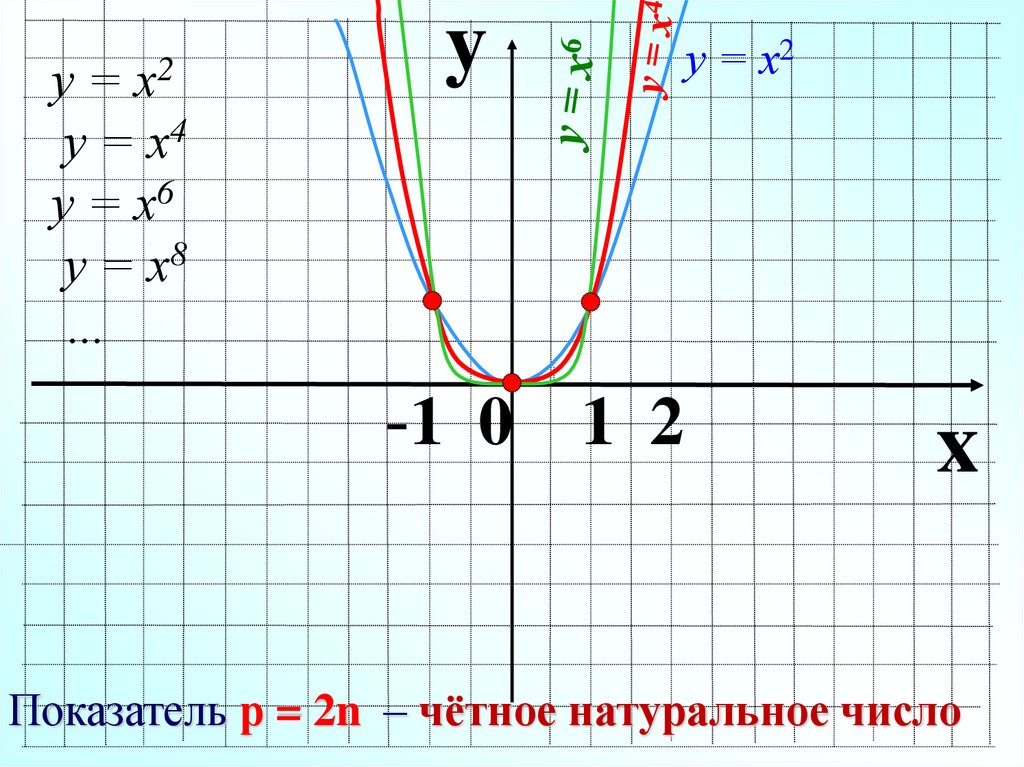
5.
у = х2у = х4
у = х6
у = х8
…
y
-1 0 1 2
у = х2
x
Показатель р = 2n – чётное натуральное число
6.
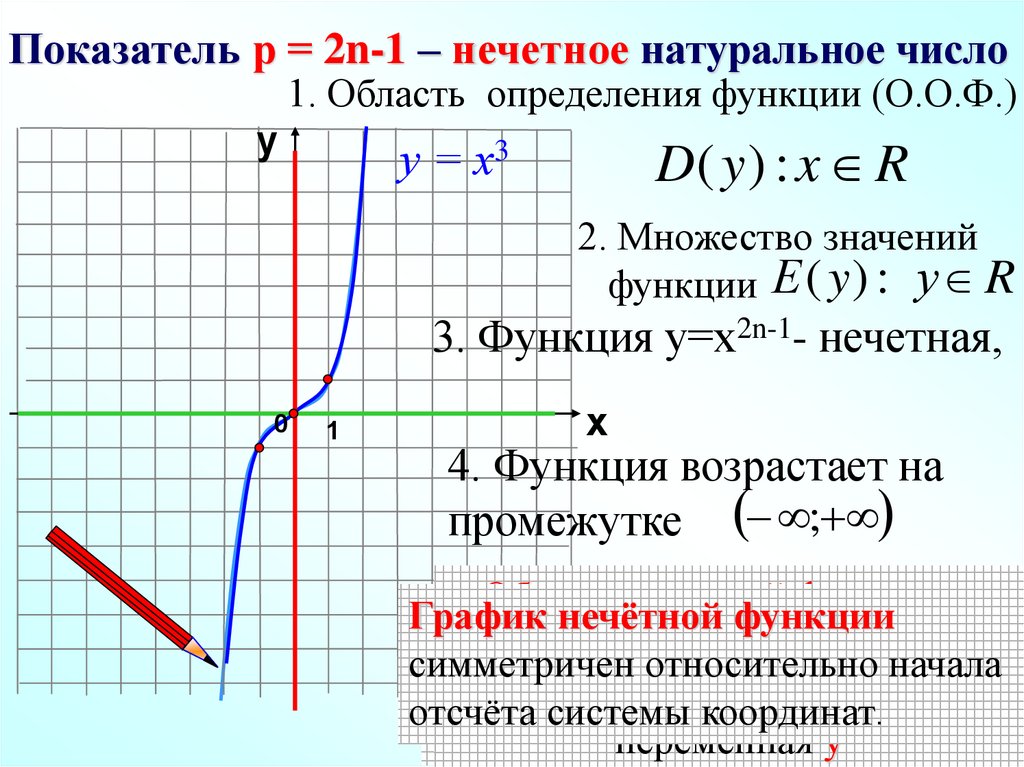
Показатель р = 2n-1 – нечетное натуральное число1. Область определения функции (О.О.Ф.)
у
D( y ) : x R
у = х3
2. Множество значений
функции Е ( y ) : у R
3. Функция у=х2n-1- нечетная,
0
1
х
4. Функция возрастает на
промежутке ;
Область
значений
функции –
График
нечётной
функции
Область
определения
функции –
множество
значений,
симметричен относительно начала
значения,может
которые
может
которые
принимать
отсчёта системы координат.
принимать
переменная
х
переменная
у
7.
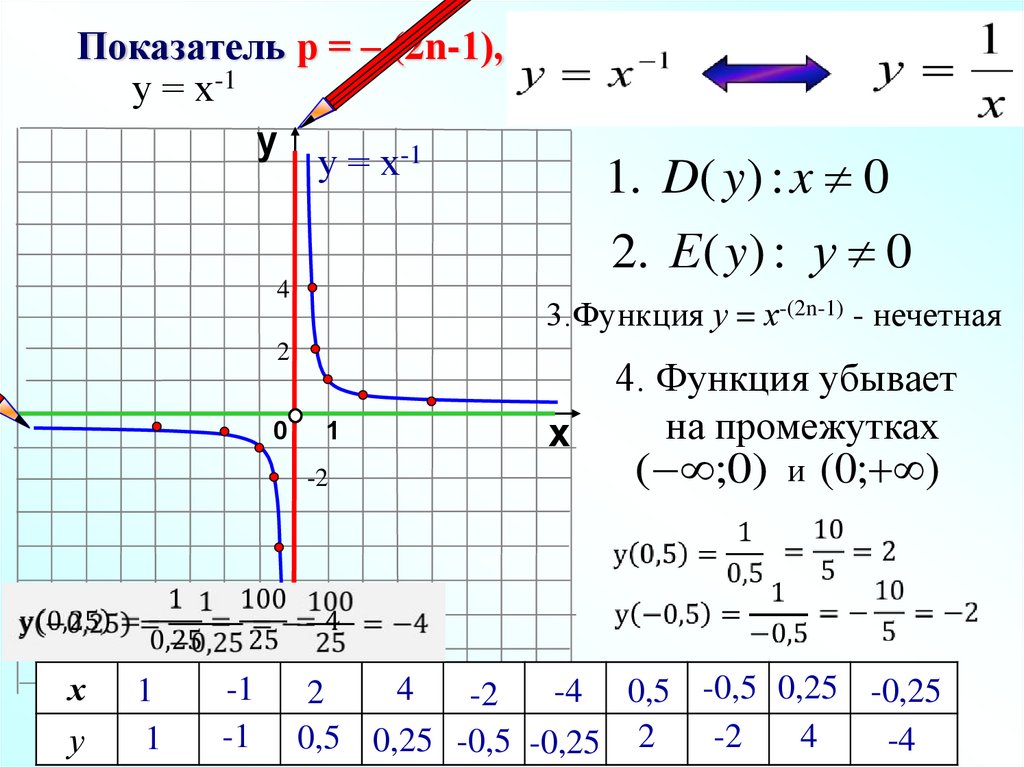
Показатель р = – (2n-1), где n – натуральное числоу = х-1 , у = х-3, у = х-5 ,
у = х-7, у = х-9, …
8.
Показатель р = – (2n-1), где n – натуральное числоу = х-1
у
у = х-1
1. D( y) : x 0
2. Е ( y) : у 0
4
3.Функция у = х-(2n-1) - нечетная
2
0
1
-2
х
у
1
1
-1
-1
х
4. Функция убывает
на промежутках
( ;0)
и
(0; )
4
-4 0,5 -0,5 0,25 -0,25
2
-2
4
-2
0,5 0,25 -0,5 -0,25 2
-4
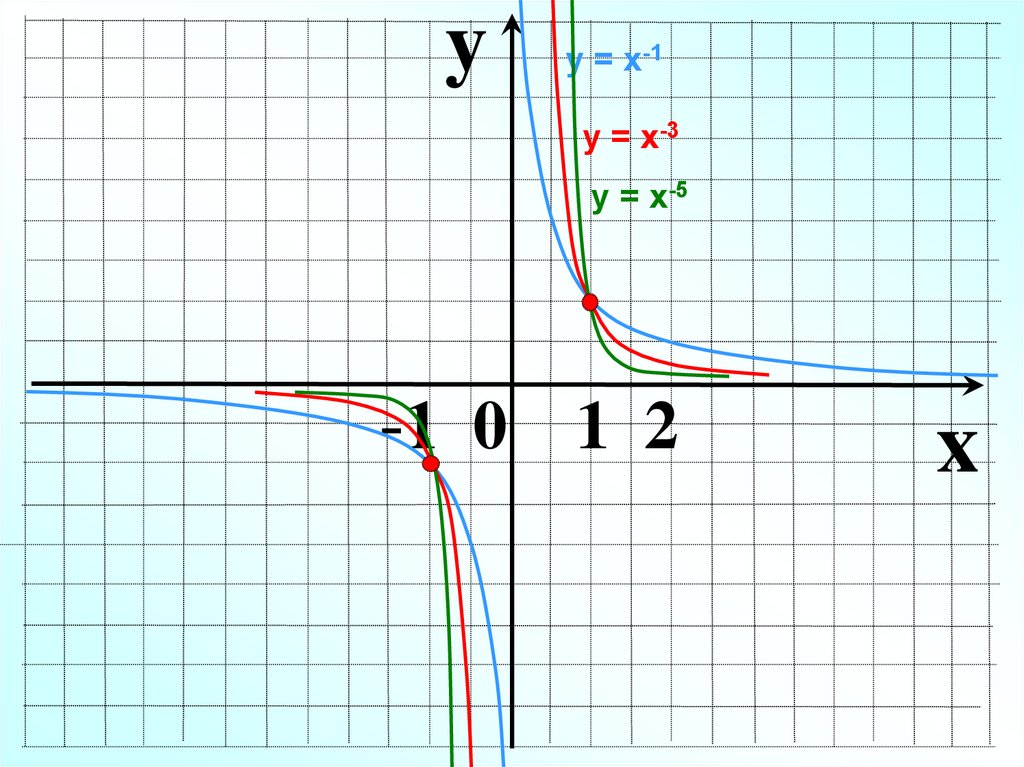
9.
yу = х-1
у = х-3
у = х-5
-1 0 1 2
x
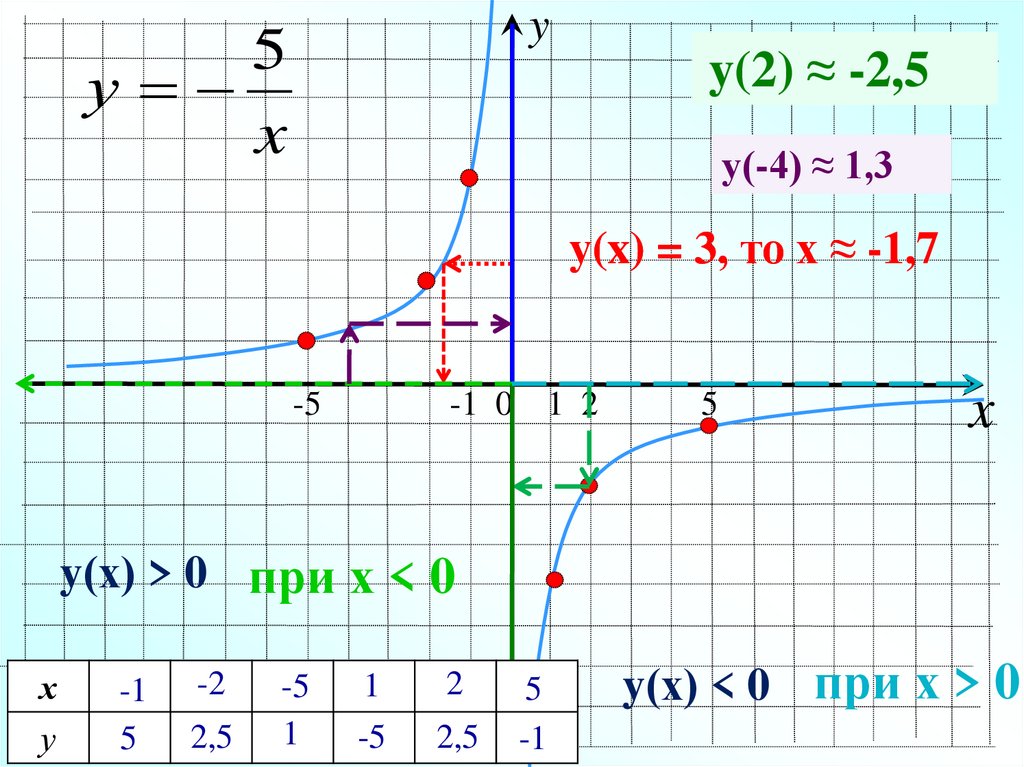
10.
y5
у
x
y(2) ≈≈ ?-2,5
y(2)
у(-4) ≈ ?1,3
у(x) = 3, то х ≈ -1,7
-5
-1 0
1 2
5
x
y(х) > 0 при х < 0
х
у
-1
5
-2
2,5
-5
1
1
-5
2
2,5
5
-1
y(х) < 0 при х > 0
11.
Домашнее задание№125, №124
12.
2 занятие13.
Проверь своё решение!у
О.О.Ф. : x 0
у=х
4
2
-1
-5
0
1
-2
-5
х
у
1
1
-1
-1
4
х
у
4
4
-5
-5
1) Графики функций
пересекаются при х = 1
и при х = -1
х
2) при х ∊ (0; 1)
и при х ∊ (-1; 0)
4
-4 0,5 -0,5 0,25 -0,25
2
-2
4
-2
0,5 0,25 -0,5 -0,25 2
-4
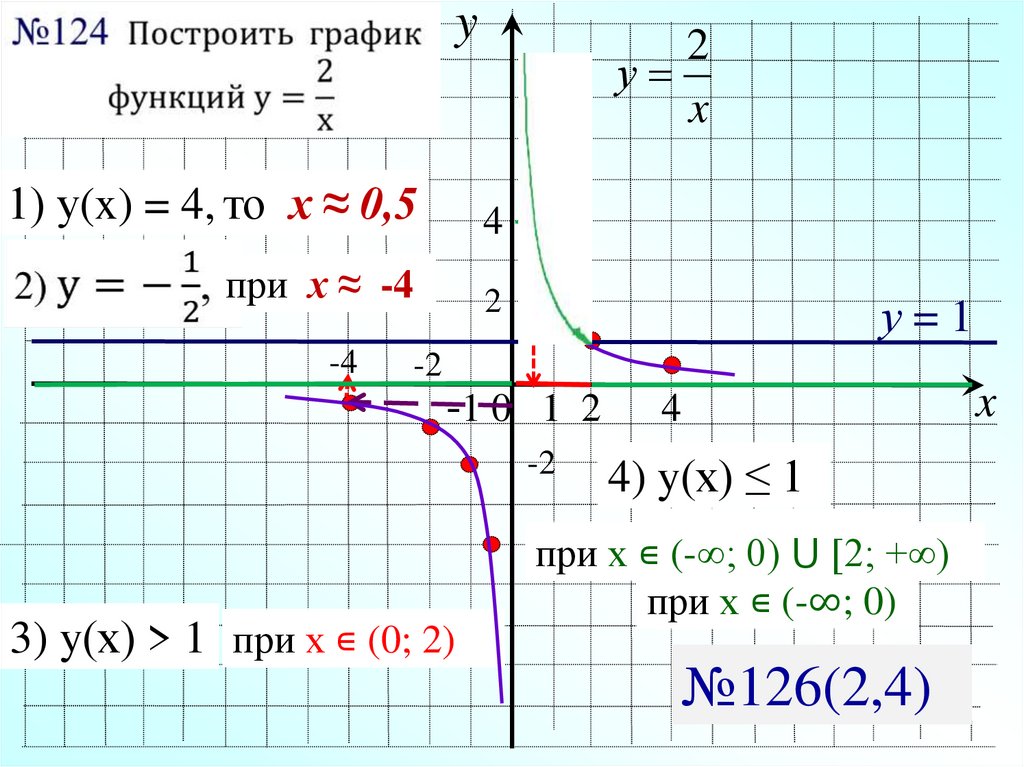
14.
y2
у
x
1) у(x) = 4, то х ≈ 0,5
4
при х ≈ -4
2
-4
у=1
-2
-1 0 1 2
-2
x
4
4) y(х) ≤ 1
∊ [2;
+∞)+∞)
-4при х ∊при
(-∞;х 0)
⋃ [2;
3) y(х) > 1 при х ∊ (0; 2)
при х ∊ (-∞; 0)
№126(2,4)
15.
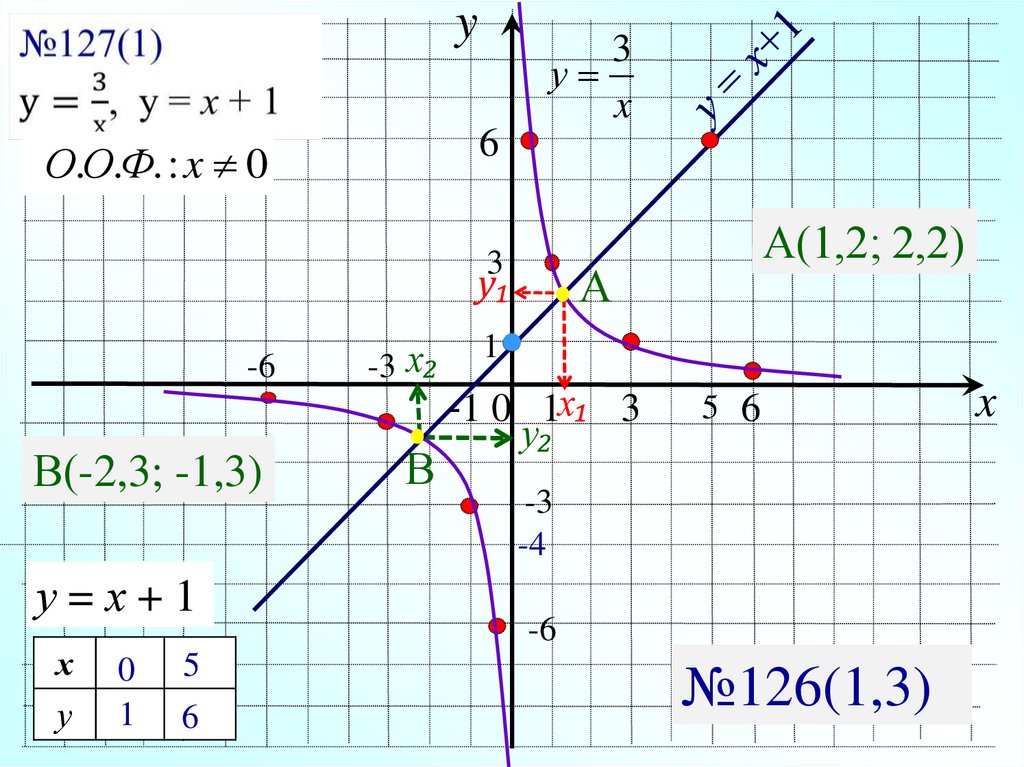
y3
у
x
6
О.О.Ф. : x 0
3
у₁
-6
В(-2,3; -1,3)
у=х+1
х
у
0
1
5
6
-3 х₂
В
А(1,2; 2,2)
А
1
-1 0 1х₁ 3
у₂
5 6
-3
-4
-6
№126(1,3)
x
16.
№126(1)№126(3)
х≠0
17.
Домашнее задание№127(2), №126(2,4)
18.
3 занятие19.
3yу
x
3
у
x
6
О.О.Ф. : x 0
3
-6
-3
1
-1 0 1
-3
-4
3
x
5 6
у=1-х
х
у
0
1
5
-4
-6
№126(2,4)
20.
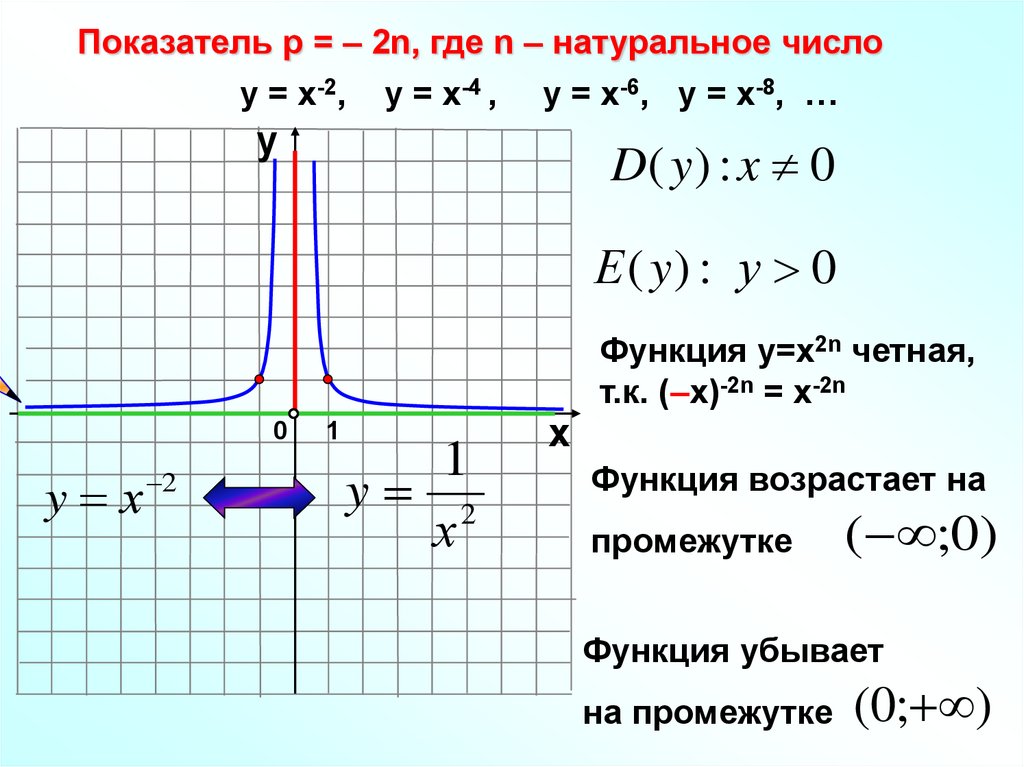
Показатель р = – 2n, где n – натуральное числоу = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2
1
1
y 2
х
х
Функция у=х2n четная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
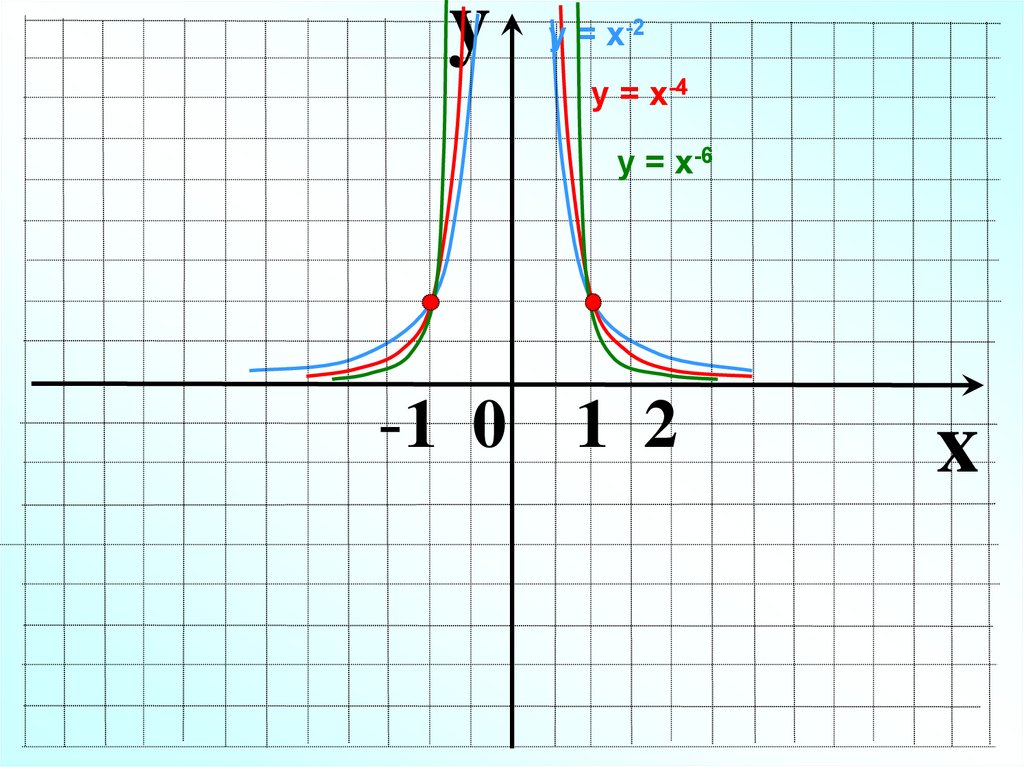
21.
yу = х-2
у = х-4
у = х-6
-1 0 1 2
x
22.
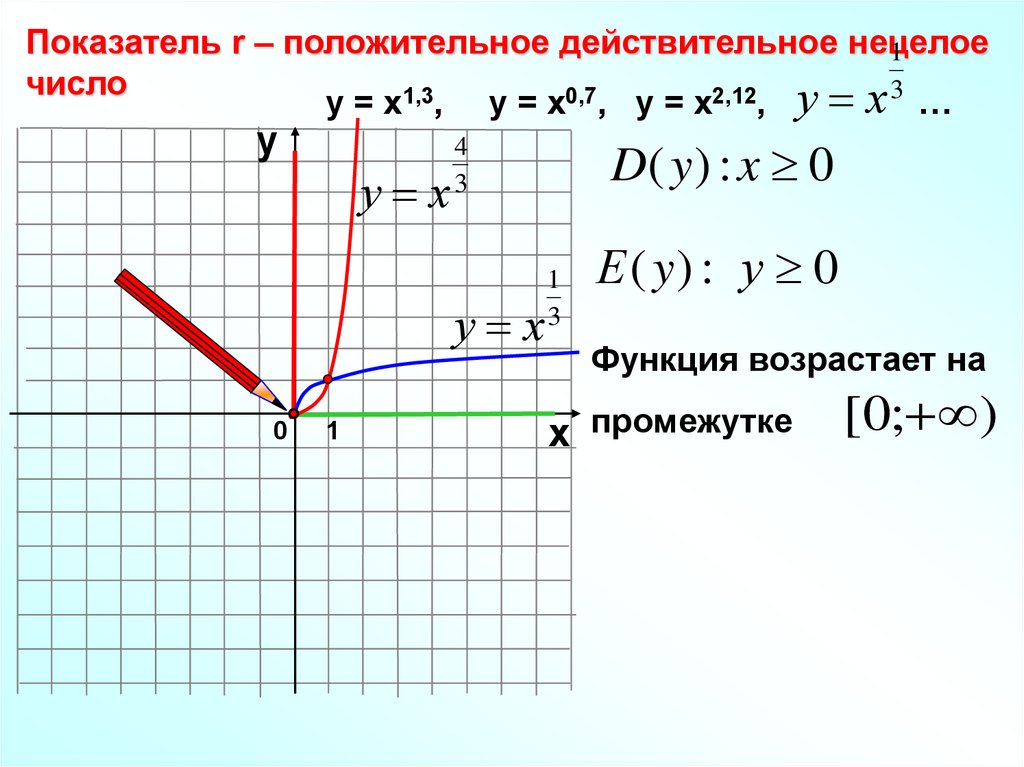
Показатель r – положительное действительное нецелое1
число
у = х1,3, у = х0,7, у = х2,12, у х 3 …
у
у х
у х
0
1
D( y ) : x 0
4
3
1
3
Е ( y) : у 0
Функция возрастает на
х промежутке
[0; )
23.
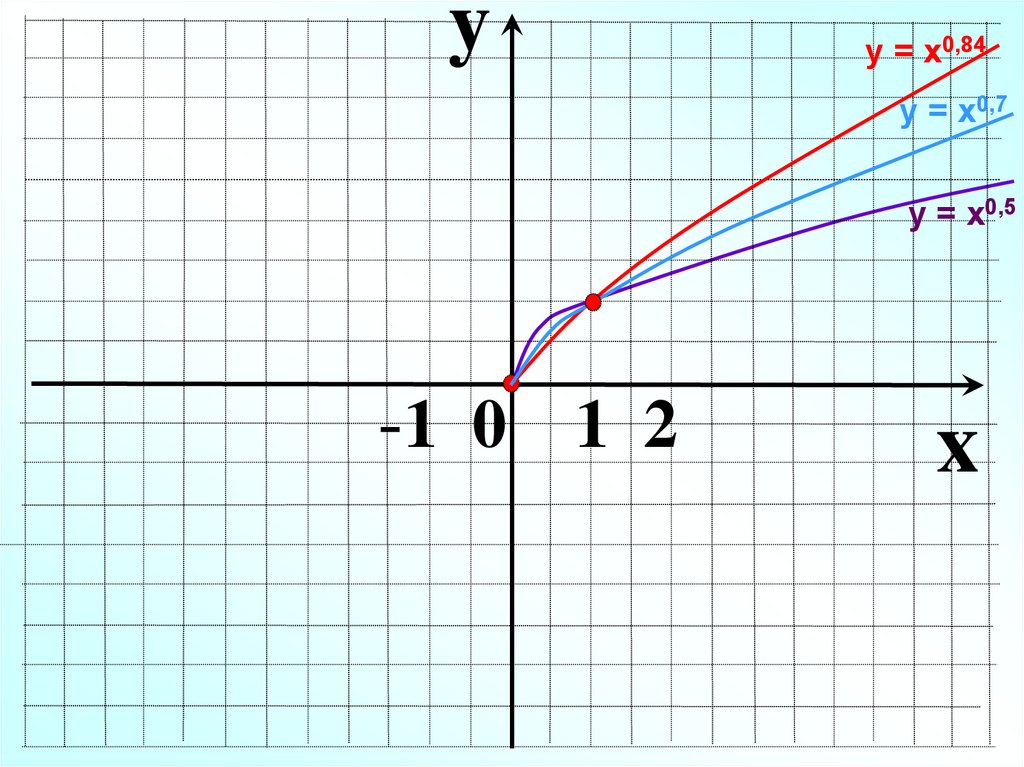
yу = х0,84
у = х0,7
у = х0,5
-1 0 1 2
x
24.
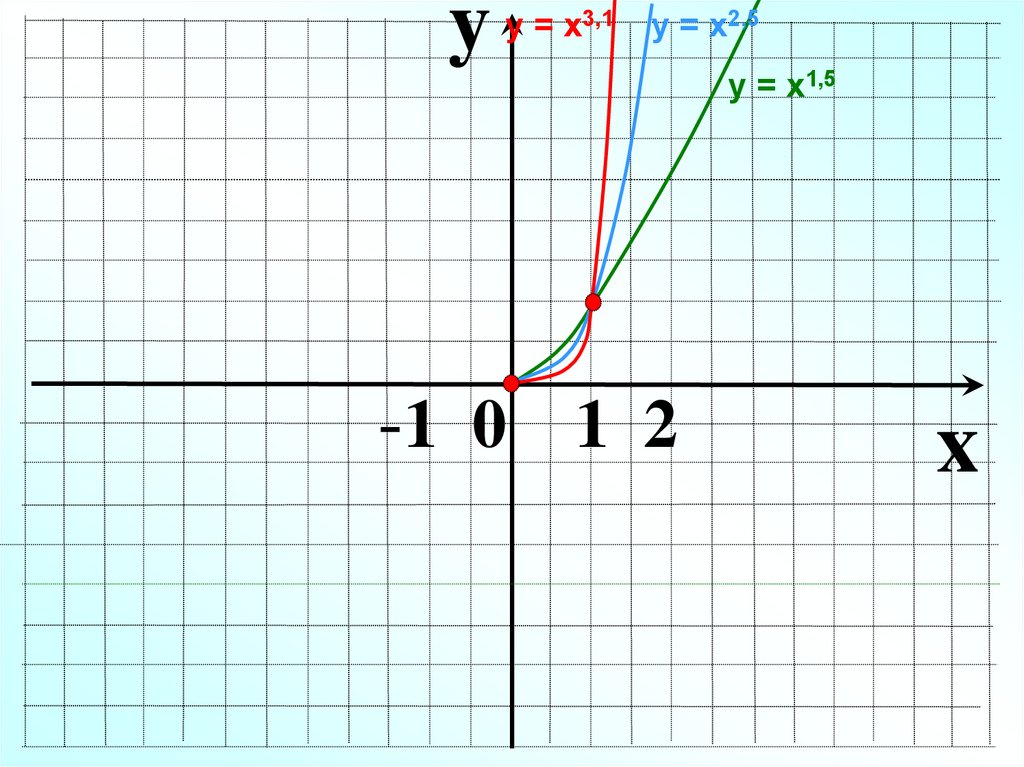
yу = х3,1
у = х2,5
-1 0 1 2
у = х1,5
x
25.
43
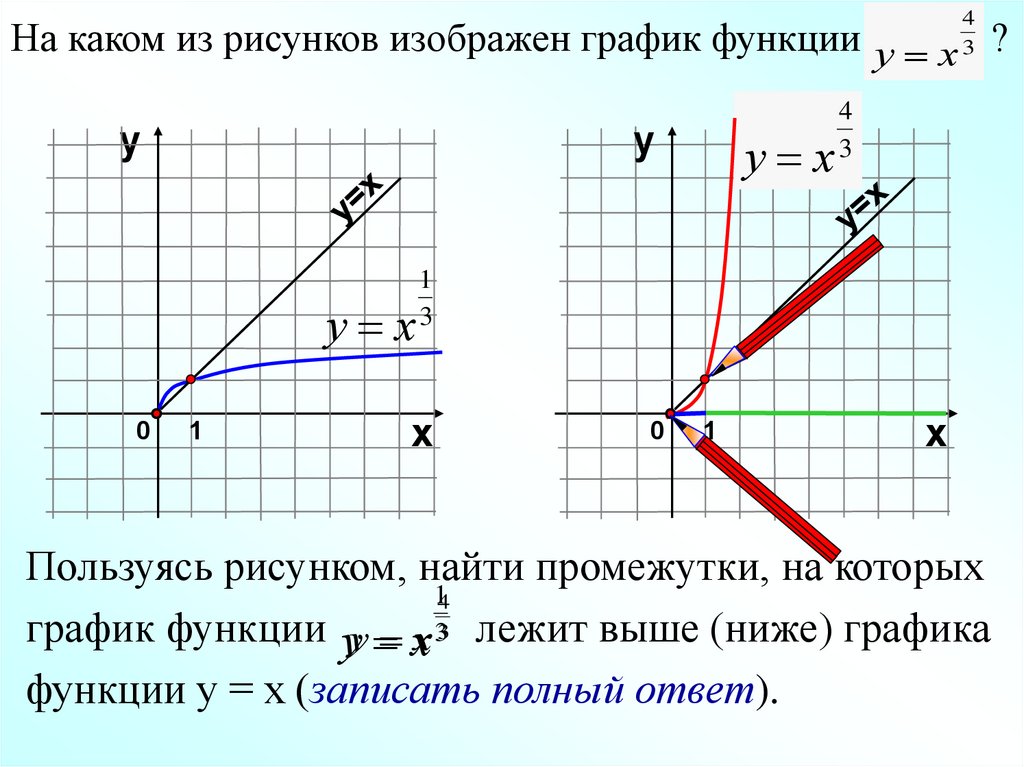
На каком из рисунков изображен график функции у х ?
у
у
у х
0
1
у х
4
3
1
3
х
0
1
х
Пользуясь рисунком, найти промежутки, на которых
14
график функции уу х 3 лежит выше (ниже) графика
функции у = х (записать полный ответ).
26.
Домашнее задание№128, №129











 Математика
Математика








