Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения

1. Лекция 22. Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения. Уравнения с

разделяющимися переменными, однородные и
сводящиеся к однородным. Линейные
уравнения. Уравнения Бернулли.
1

2.

Дифференциальные уравнения первого
порядка
§ 1. Определение дифференциальных уравнений. Понятие решения дифференциального
уравнения.
Определение 1. Уравнение вида
F(x, y(x), y (x), …, y(n)(x)) = 0
(1)
Связывающее независимую переменную х, искомую функцию y(x) и ее производные называется
обыкновенным дифференциальным уравнением.
2

3. Наличие хотя бы одной производной обязательно. Определение 2. Функция y = (x), n раз дифференцируемая на (a,b) называется

Наличие хотя бы одной производной
обязательно.
Определение 2. Функция y = (x), n раз
дифференцируемая на (a,b) называется
решением уравнения (1), если подстановка
этой функции в уравнение (1) обращает его в
тождество, т.е. F(x, (x), (x), …, (n)(x)) 0.
Пример: y + y = 0.
Его решение: y = sinx. Убедимся в этом:
y = cosx,
y = - sinx,
Тогда:
- sinx + sinx 0.
3

4.

Определение 3. Порядком дифференциального
уравнения (1) называют порядок наивысшей
производной , входящей в уравнение (1).
Пример: yIV + 3y + xy = cosx имеет четвертый
порядок.
Определение 4. Дифференциальное уравнение
вида (1) называется разрешенным относительно
старшей производной, если оно может быть
записано в виде:
y(n) = f (x, y(x), y (x), y (x), …, y(n-1)(x))
(2)
Пример: y + x = 0.
Разрешим его относительно старшей производной:
y = - x.
4

5.

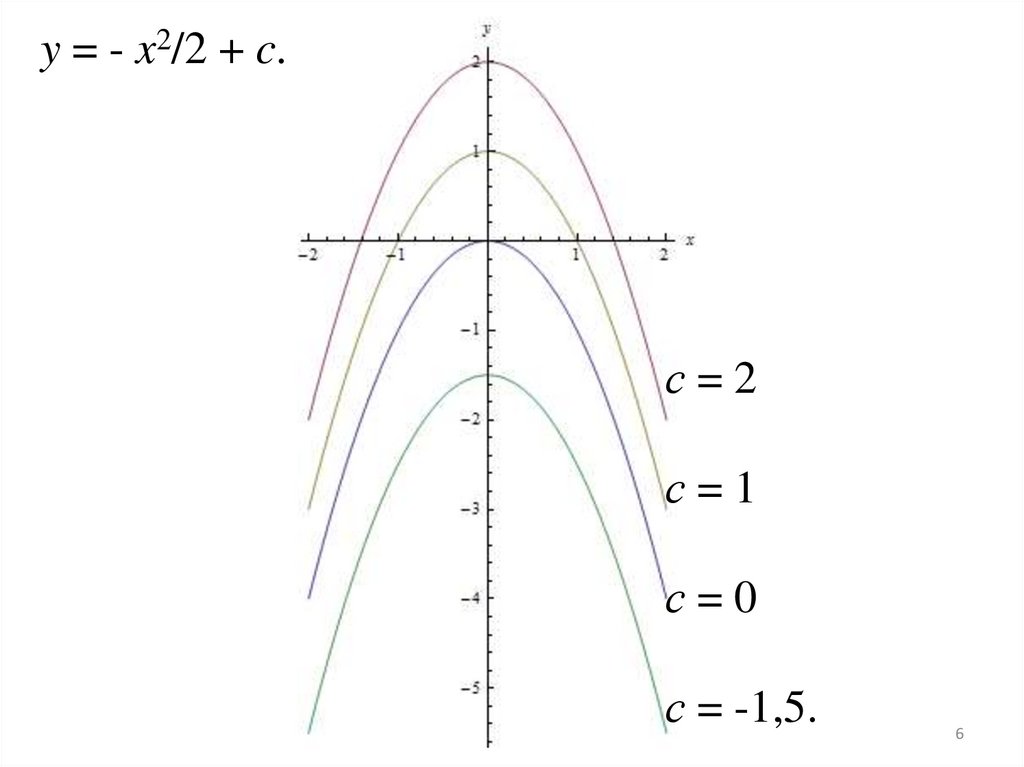
Найдем первообразную:
y = - x2/2 + c.
Это
выражение
дает
все
решения
дифференциального уравнения:
y + x = (- x2/2 + c) + x = - x + x = 0.
Определение
5.
График
решения
дифференциального уравнения называется
интегральной кривой.
Пример: для предыдущего примера, построим
несколько интегральных кривых:
5

6.

y = - x2/2 + c.
с=2
с=1
с=0
с = -1,5.
6

7.

Для выделения из множества решений
дифференциального уравнения единственного,
ставится задача Коши.
Суть задачи Коши сводится к тому, чтобы
найти решения дифференциального уравнения
вида F(x, y(x), y (x)) = 0, удовлетворяющему
начальному условию:
y(x0) = y0 y x = x0 = y0.
7

8.

Пример: Решить задачу Коши.
y x 0
y 1 1
т.е. при условии, что y(1) = 1.
Решение.
1) Находим первообразную:
y = - x2/2 + c.
2) При помощи начального условия выделим
решение задачи Коши:
y 1 1 c
3
c
2
2
x 2 3 y 1 1
Ответ: y
2 2
8

9.

Задача Коши не всегда имеет единственное
решение. Единственное решение существует
тогда и только тогда, когда выполняются
условия теоремы:
Теорема (существования и единственности).
Пусть в области D дано уравнение y = f (x,y).
Если
для
точки
M(x0,y0)
существует
окрестность, такая что:
1) f (x,y) непрерывна в ней по аргументам x и y.
2) частная производная f/ y ограничена по
f
. Тогда в этой
абсолютной величине, т.е.
y
окрестности существует
y f x, y
единственное решение задачи Коши: y x0 y0
9

10.

Геометрический смысл теоремы Коши.
Если выполняется условие теоремы в
окрестности точки M(x0,y0), то через точку
M(x0,y0) проходит единственная в окрестности
интегральная кривая (см. рис.).
Теорема Коши – локальная теорема, если в
окрестности
существует
единственное
решение задачи
Коши, то вне
окрестности может
существовать 2 и
более решений.
10

11.

Определение 6. Решение дифференциального
уравнения, в каждой точке которого нарушается
единственность называется особым решением
дифференциального уравнения.
Обычно особое решение – это огибающая всех
интегральных кривых дифференциального
уравнения.
Общим решением для y = f (x,y) является
y = (x,c), такое, что: = f (x, (x,c)).
Если общее решение записано в виде (x,y,c)=0,
то выражение называется общим интегралом
дифференциального уравнения.
11

12.

§ 2. Типы дифференциальных уравнений
первого порядка.
y = f (x) – простейший тип.
Решение его: y f x dx c
p(x)dx = q(y)dy дифференциальное уравнение с
разделёнными переменными.
Если обозначить: P(x) и Q(y) так, что:
P (x) = p(x), Q (y) = q(y), то дифференциальное
уравнение с разделенными переменными запишется в виде: dP = dQ, тогда: d(P – Q) = 0
P – Q = c, при этом:
P p x dx
p x dx q y dy c.
Q q y dy
12

13.

Пример: xdx = y2dy. Найти общий интеграл
этого дифференциального уравнения.
Решение.
2
xdx y dy
2
3
x
y
c
2
3
3x2 – 2y3 = 6c = c1*
13

14.

§ 3. Дифференциальные уравнения с
разделяющимися переменными.
Определение 7. Уравнение вида:
f1(x) 1(y)dx = f2(x) 2(y)dy
(3)
или
y x = f (x) (y)
(4)
называется дифференциальным уравнением с
разделяющимися переменными.
Очевидно, что (4) (3), так как (домножим (4)
на dx)
y xdx = f (x) (y)dx, так как: y xdx = dy, то:
dy = f (x) (y)dx.
14

15.

Уравнение (3) сводится к уравнению с
разделенными переменными.
Действительно. Разделим в (3) обе части на
f2(x) 1(y) 0, тогда:
f1 x
2 y
dx
dy - уравнение с разделенными
f2 x
1 y
переменными. Интегрируя, получаем:
f1 x
2 y
f x dx y dy c
2
1
Это выражение является общим интегралом
дифференциального уравнения с разделенными
переменными.
15

16.

§ 4. Однородные дифференциальные
уравнения первого порядка.
Предварительное замечание:
Определение 8. Функция f (x,y) называется
однородной n-го измерения, если p 0 имеет
место f (px,py) = pnf (x,y).
В частности, если n = 0, то f (px,py) = f (x,y) –
однородная функция нулевого измерения.
Теорема 1. Если P(x,y) и Q(x,y) – однородные
функции одного измерения, то
P x, y
f x, y
Q x, y
однородная функция нулевого измерения.
16

17.

Доказательство.
p 0 рассмотрим:
P px, py p n P x, y P x, y
f px, py
n
f x, y
Q px, py p Q x, y Q x, y
Ч.т.д.
Теорема 2. Однородная функция нулевого
измерения зависит лишь от отношения
переменных.
Доказательство.
1
Пусть f (px,py)=f (x,y) при p 0 рассмотрим p
x
тогда:
y
y
f x, y f 1,
x
x
Ч.т.д.
17

18.

Определение 9. Уравнение вида
P(x,y)dx + Q(x,y)dy = 0
(5)
называется однородным дифференциальным
уравнением
первого
порядка
(в
дифференциальной форме), где P(x,y) и Q(x,y)
- однородные функции одного измерения.
Действительно. Разделим (5) на Q(x,y)dx 0,
имеем: dy P x, y
dy
P x, y
0
.
dx Q x, y
dx
Q x, y
P x, y
Согласно теореме 1:
- однородная
Q x, y
18

19.

функция нулевого измерения
теореме 2:
dy
y
dx
x
и
согласно
(6)
- однородное дифференциальное уравнение
первого порядка.
Однородные дифференциальные уравнения
сводятся к уравнениям с разделяющимися
переменными путём введения новой функции:
y
u x
x
Выразим y:
y = u(x) x.
19

20.

Продифференцируем его:
dy
du
u x
dx
dx
Подставим полученное выражение в (6):
du
du
u x u x u u
dx
dx
В полученном уравнении легко разделяются
переменные:
du
dx
u u x
Получили
уравнение
с
разделенными
переменными, откуда:
du
dx
u u x ñ
Получили общее решение исходного уравнения,
если (u) – u 0, x 0.
20

21.

§ 5. Уравнения, приводящиеся к
однородному.
ax by c
dy
f
dx
a1x b1 y c1
1) Случай: если с = с1 = 0, то
a b y
ax by
dy
y
x
f
f
dx
x
a1x b1 y
a1 b1 y
x
Получили однородное уравнение.
21

22.

2) Случай: если по крайней мере одно из чисел
с или с1 0, и
a
b
a1 b1
0 тогда путем
введения новых неизвестных:
x=X+h
y = Y + k,
где: h и k – решения системы:
ax by c 0
a1x b1 y c1 0
данное уравнение сводится к однородному.
22

23.

Покажем это:
dx = dX
dy = dY.
Подставим в исходное уравнение:
=0
aX bY ah bk c
dY
f
dX
a1 X b1Y a1h b1k c1
=0
aX bY c
dY
Y
f
dX
X
a1 X b1Y c1
Получили однородное уравнение относительно
неизвестной функции Y и:
Y
u
X
23

24.

3) Случай: если одно из чисел с или с1 0, а
a b
0
a1 b1
a1 b1
тогда ab1 = a1b k a1 = ak и b1 = bk,
a b
ax by c
dy
тогда: f
dx
k ax by c1
путём введения новой функции
z(x) = ax + by
данное уравнение сводится к уравнению с
разделяющимися переменными.
24

25.

Покажем это:
dz
dy
z x ax by a b
dx
dx
dy dz
dy 1 dz
b a a
dx dx
dx b dx
Подставим все в исходное уравнение:
1 dz
z c 1 dz
a f
a z
b dx
kz c b dx
dz
dz
a b z b z a
dx
dx
dz
dz
dx
dx c
b z a
b z a
Получили общий интеграл.
25

26.

§ 6. Линейные дифференциальные
уравнения первого порядка.
Определение 10. Уравнение вида
dy
+ P(x)y = Q(x)
dx
(7)
где P(x) и Q(x) - непрерывные функции,
называется линейным дифференциальным
уравнением первого порядка (относительно
неизвестной функции y(x)).
Будем искать решение уравнения в виде
произведения двух функций:
26

27.

y(x) = u(x) v(x)
где одну функцию можно взять произвольно с
таким расчетом, чтобы уравнение упростилось,
а вторую подобрать так, чтобы произведение
этих двух функций являлось решением.
Найдем:
dy
dv
du
u v
dx
dx
dx
Подставим всё в (7):
dv
du
u v P x uv Q x
dx
dx
dv du
u v P x u Q x (*)
dx dx
27

28.

Подберем функцию u так, чтобы:
du
P x u 0
dx
Для этого в качестве u возьмем какое-либо
решение уравнения:
du
du
du
P x u 0
P x dx P x dx
dx
u
u
ln u P x dx u e P x dx
Подставим полученное значение u в (*):
P x dx dv
P x dx
e
Q x dv Q x e
dx
dx
P x dx
P x dx
dv Q x e
dx c v Q x e
dx c
28

29.

Общее решение:
y = u v =
e P x dx Q x e P x dxdx c
Замечание: Уравнение вида:
dx
+ P(y)x = Q(y)
dy
относительно x(y). Его решение ищется в виде:
x(y) = u(y) v(y)
29

30.

§ 7. Уравнение Бернулли.
Определение 11. Уравнение вида
dy
+ P(x)y = Q(x)y
dx
(8)
где P(x) и Q(x) - непрерывные функции и
0, 1, называется уравнением Бернулли.
Уравнение Бернулли сводится к линейному:
делим все члены уравнения на y :
y-
dy
+ P(x)y1- = Q(x)
dx
(**)
30

31.

Обозначим: y1- = z и продифференцируем:
1 dz
dy dz
dy
1 y
y
dx dx
dx 1 dx
Подставим полученное выражение в уравнение
(**):
1 dz
P x z Q x
1 dx
Получили
линейное
дифференциальное
уравнение первого порядка относительно
функции z(x).
31