Похожие презентации:
Частные производные и их геометрические интерпретации. Полный дифференциал функции нескольких переменных
1.
1.2. Частные производные и их геометрическиеинтерпретации. Полный дифференциал функции
нескольких переменных.
1. Частные производные и их геометрические интерпретации.
2. Полный дифференциал функции нескольких переменных и
его приложения в приближенных вычислениях.
2.
Дадим аргументу х приращение Δх, а аргументу уприращение Δу.
Тогда функция z получит значение
f ( x x, y y )
Величина
z f ( x x, y y ) f ( x, y )
называется полным приращением функции в
точке (х,у).
3.
Если задать только приращение х или у, тоx z f ( x x, y) f ( x, y)
y z f ( x, y y ) f ( x, y )
- частные приращения функции.
4.
Полное приращение функции в общем случаене равно суме частных приращений:
z x z y z
5.
Найти полное и частные приращенияфункции
z x y
6.
x z ( x x) y x yx y x y x y x y
y z x ( y y ) x y
x y x y x y x y
7.
z ( x x) ( y y ) x yx y x y x y x y x y
x y x y x y
Действительно
z x z y z
8.
Частной производной функции несколькихпеременных по одной из этих переменных
называется предел отношения
соответствующего частного приращения
функции к приращению рассматриваемой
независимой переменной, при стремлении
приращения переменной к нулю.
z x , z y ,
z
,
x
z
,
y
f x ( xy),
f y ( xy)
9.
xzf ( x x, y ) f ( x, y )
z x lim
lim
x 0 x
x 0
x
yz
f ( x, y y) f ( x, y)
z y lim
lim
y 0 y
y 0
y
10.
Из определения частной производной следует, чтодля нахождения производной
z x
нужно считать постоянной переменную у, а для
нахождения производной z y
нужно считать постоянной переменную х.
При
нахождении
частных
производных
сохраняются
известные
ранее
правила
дифференцирования.
11.
12.
Найти частные производныефункции
y
z x ln y
x
13.
zy
z x
ln y 2
x
x
z x 1
z y
y y x
14.
Введем понятие частных производных второгопорядка.
Если частные производные
z
z x
x
и
z
z y
y
сами являются дифференцируемыми функциями,
то можно найти их частные производные,
которые называются частными производными
второго порядка:
15.
zz xx f xx ( xy) 2
x
2
z
z yy f yy ( xy) 2
y
2
16.
Можнотакже
производные:
определить
смешанные
z
z xy f xy ( xy)
x y
2
z
z yx f yx ( xy)
y x
2
17.
Если частные производные второго порядкафункции z=f(x,y) непрерывны в точке (х0,у0),
то в этой точке смешанные производные
равны:
f xy ( x0 , y0 ) f yx ( x0 , y0 )
18.
Вычислить частные производныевторого порядка функции
z 3x x sin y
2
в точке (1,0).
19.
zz x
6 x sin y
x
z
z y
x cos y
y
z
z xx
6
2
x
z
z yy 2 x sin y
y
2
2 z
z xy
cos y
x y
2
2 z
z yx
cos y
y x
20.
z xx (1,0) 6z xy (1,0) 0
z yy (1,0) 0
(1,0) 0
z yx
21.
Дифференциалом функции называетсясумма произведений частных
производных этой функции на
приращения соответствующих
независимых переменных.
22.
dz z x x z y ydz z x dx z y dy
z
z
dz
x
y
x
y
23.
Функция z=f(x,y) называетсядифференцируемой в точке (x,y), если
ее полное приращение можно
представить в виде:
z dz x y
24.
Где dz – дифференциал функции;( x, y )
( x, y )
- бесконечно малые величины при
x 0
и
y 0
Таким
образом,
дифференциал
функции
нескольких переменных – это главная, линейная
относительно приращений Δх и Δу часть полного
приращения функции.
25.
Дляфункции
одной
переменной
существование конечной производной
y=f(x)
f (x )
и представление приращения функции в виде
y dy ( x) x
являются равнозначными утверждениями.
Для
функции
нескольких
переменных
существование частных производных является
необходимым но не достаточным условием
дифференцируемости функции.
26.
Если частные производные функцииz=f(x,y) существуют в некоторой
окрестности точки (x,y) и непрерывны
в самой точке (x,y), то функция
z=f(x,y) дифференцируема в этой точке.





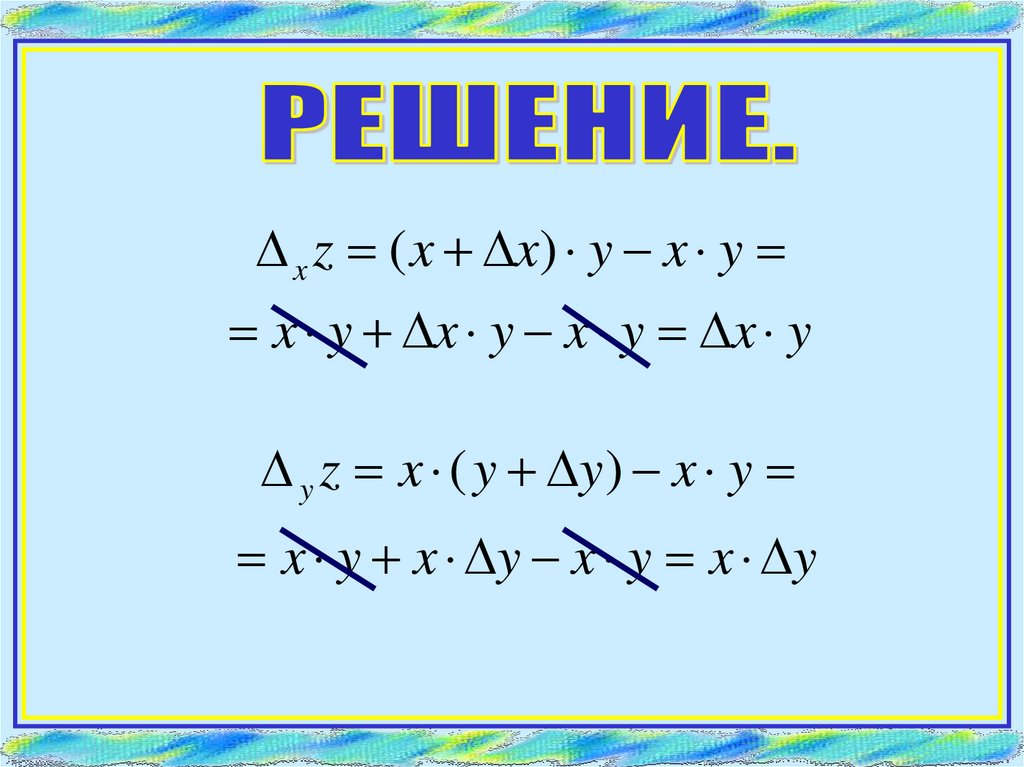













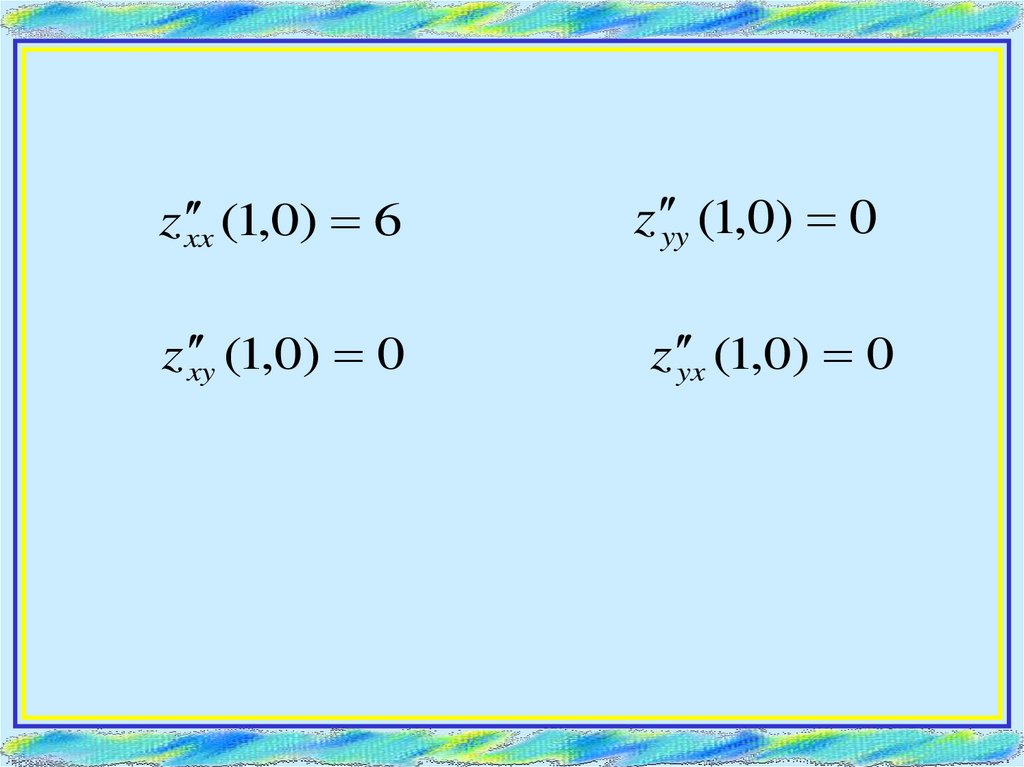






 Математика
Математика








