Функции нескольких переменных, область определения. Частные производные. Полный дифференциал. Лекция №1-2

1. ЛЕКЦИЯ №1-2

Функции нескольких переменных,
область определения.
Частные производные.
Полный дифференциал.

2. Определение функции двух переменных

Если каждой паре (х,у) значений двух не зависимых друг от друга
переменных величин х и у из некоторой области их изменения D,
соответствует определенное значение величины z, то говорят, что z есть
функция двух независимых переменных х и у, определенная в области D:
z f ( x; y ),
z F ( x; y )
Примеры.
1) Площадь S прямоугольника со сторонами, длины которых равны х и у ,
выражается формулой S xy . Каждой паре значений х и у соответствует
определенное значение площади S, т.е. S есть функция двух переменных.
2) Объем V прямоугольного параллелепипеда с ребрами, длины которых
равны x, y, z выражается формулой V xyz . В данном примере V является
функцией трех переменных.

3.

Совокупность пар (х; у) значений х и у , при которых определяется
функция z f ( x; y ) , называется областью определения или областью
существования этой функции. Обозначение: D(z) или D(f).
Область определения наглядно иллюстрируется геометрически: если
каждую пару значений х и у мы будем изображать точкой M(x;y) в плоскости
Оху, то область определения функции изобразится в виде некоторой
совокупности точек на плоскости. Эту совокупность точек будем называть
также областью определения функции.
Линию, ограничивающую данную область будем называть границей
области.
Точки области, не лежащие на границе, называются внутренними
точками области.
Область, состоящая только из внутренних точек области называется
открытой или незамкнутой.
Если же к области относятся и точки границы, то область называется
замкнутой.

4.

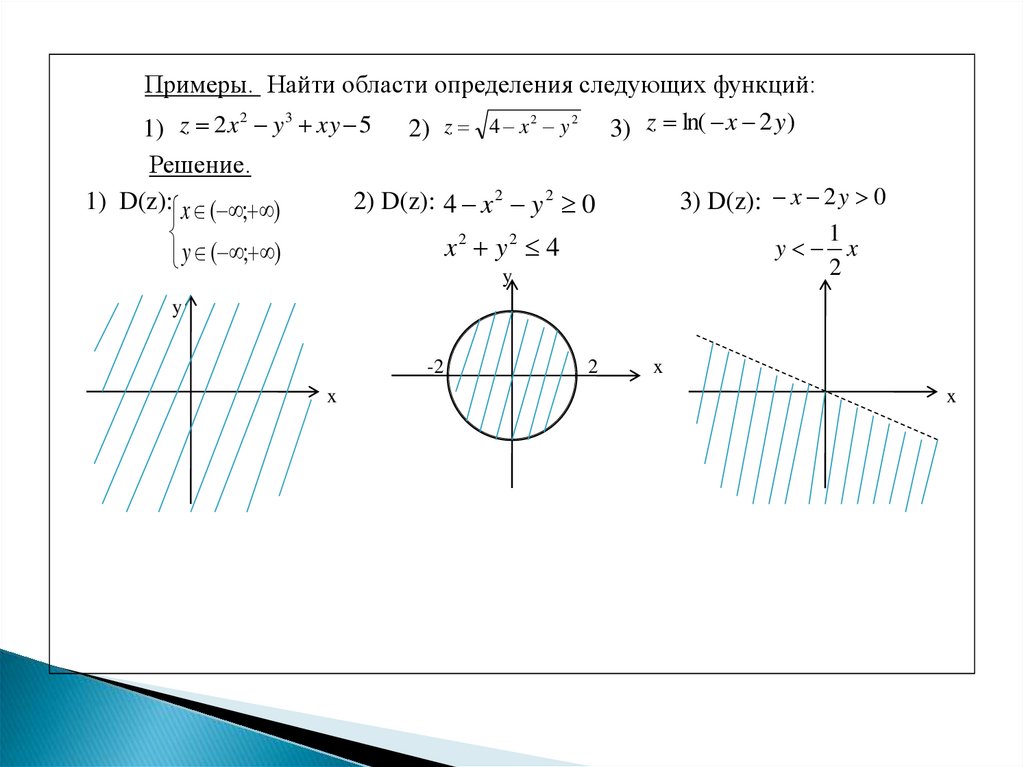
Примеры. Найти области определения следующих функций:
2
3
1) z 2 x y xy 5 2) z 4 x 2 y 2 3) z ln( x 2 y )
Решение.
1) D(z): x ( ; )
3) D(z): x 2 y 0
2) D(z): 4 x 2 y 2 0
y ( ; )
1
y x
2
x2 y2 4
y
y
-2
x
2
x
x

5. Геометрическое изображение функции двух переменных

Рассмотрим функцию z f ( x; y) , определенную в области D на
плоскости Оху.
z
( x; y; z )
В каждой точке (х;у) восставим перпендикуляр к
плоскости Оху и на нем отложим отрезок, равный f ( x; y )
f ( x; y )
Тогда мы получим в пространстве точку Р с координатами
( x; y; z f ( x, y ))
у
Геометрическое место точек Р, координаты которых
удовлетворяют уравнению z f ( x; y ) , называется графиком
( x; y )
D
функции двух переменных . График функции двух переменных
представляет собой некоторую поверхность, проектирующая на плоскость Оху в
область определения функции.
Пример. Графиком функции
z
2
2
z x y является параболоид вращения.
y
x

6. Частные производные функции двух переменных

Пусть задана функция z f ( x; y) .
Дадим переменной х приращение x , а переменную у оставим без
изменения, тогда функция z получит приращение, которое называется
частным приращением функции z по переменной х и обозначается x z :
x z f ( x x; y) f ( x; y)
Аналогично определяется частное приращение функции z по у:
y z f ( x; y y ) f ( x; y )
Если обе переменные получают приращения x и y , то функция z
получит приращение, которое называется полным приращением функции z и
определяется равенством:
z f ( x x; y y ) f ( x; y )

7.

Частной производной функции z по переменной х называется предел
отношения частного приращения функции z по переменной х к приращению
переменной х когда приращение переменной х стремится к нулю:
z
z
f ( x x; y ) f ( x; y )
lim x lim
x x 0 x x 0
x
Частная производная функции z по переменной х – это производная,
вычисленная при условии, что у является постоянной величиной.
Частной производной функции z по переменной у называется предел
отношения частного приращения функции z по переменной у к приращению
переменной у когда приращение переменной у стремится к нулю:
yz
z
f ( x; y y) f ( x; y)
lim
lim
y y 0 y y 0
y
Частная производная функции z по переменной у – это производная,
вычисленная при условии, что х является постоянной величиной.

8. Примеры

Найти частные производные следующих функций:
3 2
1) z 2x y 4x y 7 x 6 y 2
2) z x 2 cos y x y
Решение.
z
3 2
y
const
2
x
y
4
x
y
x
x 7 x x 6 y x 2 x
1)
x
2 y 2 x 3 x 4 y x x 7( x) x 0 0
2 y 2 3 x 2 4 y 1 7 6 x 2 y 2 4 y 7
z
x const 2 x 3 y 2 y 4 x y y 7 x y 6 y y 2 y
y
3
2
2 x y y 4 x y y 0 6( y ) y 0
2 x3 2 y 4 x
1
2 y
6 4 x3 y
3) z sin 1 2 xy3
2x
6
y

9.

2)
z
y const x 2 cos y x y x x 2 cos y x x y x
x
2
y
cos y x x x x 2 x cos y y x y 1
z
x const x 2 cos y x y y x 2 cos y y x y y
y
x 2 cos y y x y y x 2 ( sin y ) x y ln x
x 2 sin y x y ln x
3)
z
sin 1 2 xy3 x cos 1 2 xy3 1 2 xy3 x 2 y 3 cos 1 2 xy3
x
z
sin 1 2 xy3 y cos 1 2 xy3 1 2 xy3 y 6 xy2 cos 1 2 xy3
y

10. Частные производные высших порядков

Частные производные первого порядка можно рассматривать как
функции от переменных х и у . Эти функции также могут иметь частные
производные, которые называются частными производными второго
порядка.
Они определяются и обозначаются следующим образом:
z 2 z
z xx f xx ( x; y) ;
x x x 2
z 2 z
f yx ( x; y ) ;
z yx
x y y x
z 2 z
f yy ( x; y )
2 z yy
y y y
z 2 z
z xy f xy ( x; y)
y x x y
Частные производные второго порядка по различным переменным
называются смешанными частными производными:
2 z
z xy
x y
2 z
z yx
y x

11. Пример. Найти частные производные второго порядка функции

z y 2e x 4 xy3 ln x
Решение. Находим сначала частные производные первого порядка
z
1
y 2 e x 4 xy3 ln x x y 2 e x 4 y 3
x
x
z
y 2 e x 4 xy3 ln x y 2 ye x 12 xy2
y
Частные производные второго порядка будут равны:
z 2 x
1
1
3
2 x
y
e
4
y
y
e
x
x 2
x
x2
2
2 z 2 x
1
3
y e 4 y y 2 ye x 12 y 2
x y
x
Получили
2 z
x
2
x
2
ye
12
xy
y 2e 24 xy
2
y
2 z
2 ye x 12 xy2 x 2 ye x 12 y 2
y x
2 z
2 z ,
x y y x
т.е смешанные частные производные равны между собой.

12. Полный дифференциал функции двух переменных

По определению полного приращения z f ( x x; y y ) f ( x; y ) .
Функция z f ( x; y) называется дифференцируемой в точке M ( x; y ) , если
её полное приращение можно представить в виде
z
z
z
x y x y
x
y
где 0, 0 при x 0, y 0 .
Сумма первых двух слагаемых представляет главную часть
приращения функции.
Главная часть приращения функции, линейная относительно x и y ,
называется полным дифференциалом этой функции и обозначается:
dz
z
z
x
y
x
y
Для независимых переменных х и у полагают x dx, y dy ,
поэтому полный дифференциал можно записать в виде:
dz
z
z
dx
dy
x
y

13. Применение полного дифференциала к приближенным вычислениям

Из определения дифференциала функции следует, что при достаточно
малых x и y имеет место приближенное равенство
z dz
Так как полное приращение z f ( x x; y y ) f ( x; y ) , то
приближенное равенство можно записать в следующем виде:
f ( x x; y y ) f ( x; y ) z x x z y y
(*)
Эта формула применяется в приближенных вычислениях.
Пример. Вычислить приближенно 2,013,02 .
y
Решение. Введем функцию z x , тогда требуется найти z (2,01; 3,02) .
x x 2,01, y y 3,02, x 2, x 0,01, y 3, . y 0,2
Т.е.
Находим частные производные z x yx y 1, z y x y ln x . Далее вычисляем
z(2;3) 23 8, z x (2;3) 3 23 1 12, z y 23 ln 2 8 0,69 5,52
Подставив найденные значения в формулу (*), получим:
2,013,02 8 12 0,01 5,52 0,02 8 0,12 0,11 8,23