Похожие презентации:
Готовимся к экзамену (модуль). График функции. Часть 2
1.
Готовимся к экзамену(МОДУЛЬ)
Каратанова Марина Николаевна
МКОУ СОШ №256 ГО ЗАТО г.Фокино
Приморский край
Часть 2
№23
2.
1*2*
3
4
5
6
1*
2*
3
4
5
6
1*
2*
3
4
5
6
1*
2*
3
4
5
6
3.
Какое наибольшее число общих точек может иметь графикданной функции с прямой, параллельной оси абсцисс?
y x x 2
2
Алгоритм (2):
1*
1. Построить график функции у = х² – х – 2
Ох : у 0; х2 х 2 0
х1 1; х2 2
х1 х2 1
Вершина : х0
;
2
2
2
1 1 1
у 2 2,25
2 2 2
2. Определить наибольшее
число общих точек.
Ответ:
4
2,25
-1
-2,25
0,5
2
4.
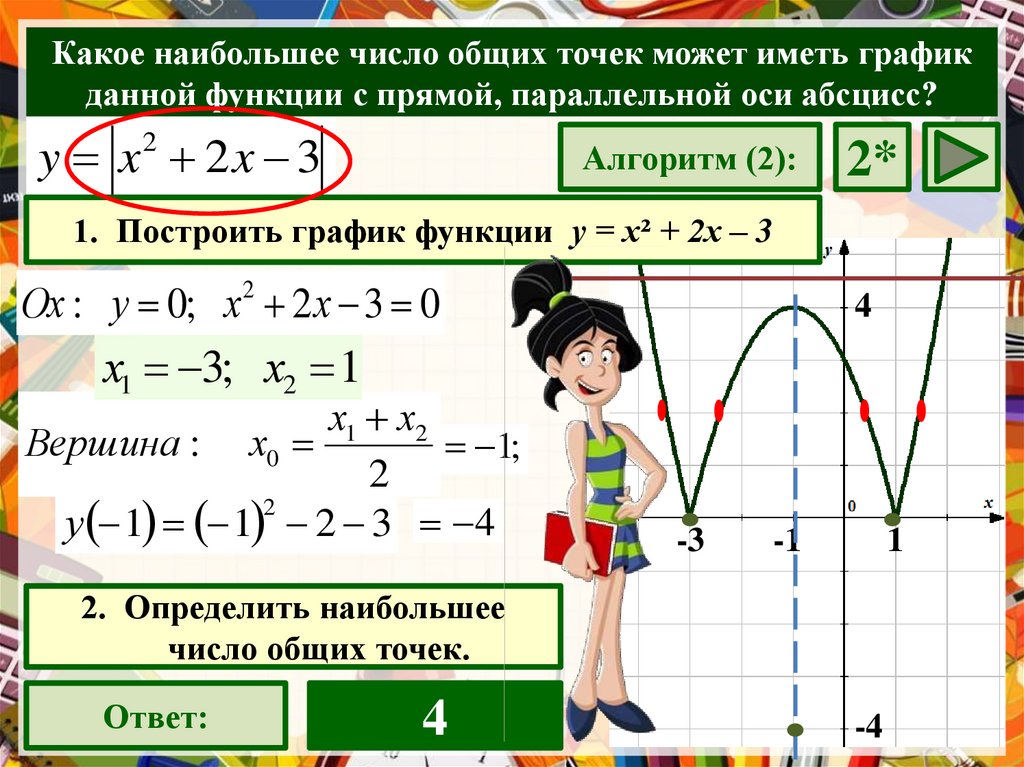
Какое наибольшее число общих точек может иметь графикданной функции с прямой, параллельной оси абсцисс?
y x 2x 3
2
Алгоритм (2):
2*
1. Построить график функции у = х² + 2х – 3
Ох : у 0; х 2 2 х 3 0
4
х1 3; х2 1
х1 х2
Вершина : х0
1;
2
2
у 1 1 2 3 4
-3
-1
1
2. Определить наибольшее
число общих точек.
Ответ:
4
-4
5.
Какое наибольшее число общих точек может иметь графикданной функции с прямой, параллельной оси абсцисс?
y x 4x 3
2
Проверка (2):
3
1. Построить график функции у = х² – 4х + 3
Ох : у 0; х 2 4 х 3 0
х1 1; х2 3
х1 х2
Вершина : х0
2;
2
у 2 22 4 2 3 1
1
2. Определить наибольшее
число общих точек.
Ответ:
4
-1
1 2
3
6.
Какое наибольшее число общих точек может иметь графикданной функции с прямой, параллельной оси абсцисс?
y x 5x 4
2
Проверка (2):
4
1. Построить график функции у = х² + 5х + 4
Ох : у 0; х 2 5х 4 0
х1 1; х2 4
х1 х2
Вершина : х0
2,5;
2
2
у 2,5 2,5 5 2,5 4
2,25
2. Определить наибольшее
число общих точек.
Ответ:
4
2,25
-4 -2,5
-1
-2,25
7.
Какое наибольшее число общих точек может иметь графикданной функции с прямой, параллельной оси абсцисс?
y x 6x 5
2
Проверка (2):
5
1. Построить график функции у = х² + 5х + 4
Ох : у 0; х 2 6 х 5 0
4
х1 1; х2 5
Вершина :
х1 х2
х0
3;
2
у 3 32 6 3 5 4
1
2. Определить наибольшее
число общих точек.
Ответ:
4
-4
3
5
8.
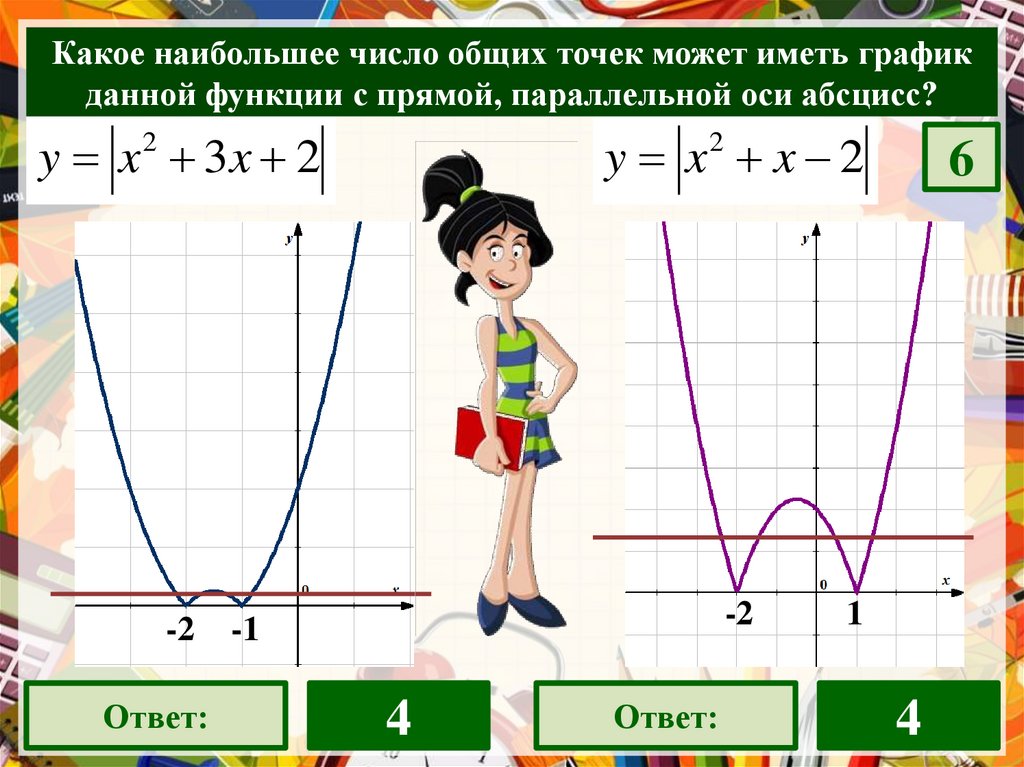
Какое наибольшее число общих точек может иметь графикданной функции с прямой, параллельной оси абсцисс?
y x 3x 2
y x x 2
-2
-2
2
Ответ:
2
-1
4
Ответ:
6
1
4
9.
хy
2
При каких значениях т прямая
y = т не имеет с графиком ни
одной общей точки
3х х
x 3
Алгоритм (3):
1. Упростить выражение
а, если а 0
а2
ха х 03 х
х 3
х
х
а
,
если
х х х 3
х 3
х 3
2. Раскрываем модуль по определению
2
х
, если х 0
х х 2
x , если х 0
1*
у х2
х 0
-3
3. Определить т
Если х 3, то у 3 9
2
Ответ:
т=-9
у х2
х 0
т 9
10.
0,25 хy
х х
x 4
2
Алгоритм (3):
При каких значениях т прямая
y = т не имеет с графиком ни
одной общей точки
1. Упростить выражение
а, если а 0
х 4
а 2
0,25 х а,хесли
х а 0,025 х х 4 х
0,25х х
х 4
х 4
2. Раскрываем модуль по определению
2
0,25
х
, если х 0
0,25 х х
2
0
,
25
x
, если х 0
2*
у 0,25 х 2
х 0
т 4
3. Определить т
4
Если х 4, то у 0,25 4 4
2
Ответ:
т=4
у 0,25 х 2
х 0
11.
хy
2
При каких значениях т прямая
y = т не имеет с графиком ни
одной общей точки
х х
x 1
Проверка (3):
1. Упростить выражение
а, если а 0
а 2
х х а,хеслиха х 01 х
х х
х 1
х 1
х 1
2. Раскрываем модуль по определению
3
2
х
, если х 0
х х 2
x , если х 0
2
Если х 1, то у 1 1
т=1
х 0
т 1
1
3. Определить т
Ответ:
у х2
у х2
х 0
12.
0,5 хy
х х
x 2
2
Проверка (3):
При каких значениях т прямая
y = т не имеет с графиком ни
одной общей точки
1. Упростить выражение
а, если а 0
х 2
а 2
0,5 х ах, если
х а 0 ,50х х 2 х
0,5х х
х 2
х 2
2. Раскрываем модуль по определению
4
у 0,5 х 2
х 0
2
0,5 х , если х 0
0,5 х х
2
0
,
5
x
, если х 0
т 2
3. Определить т
2
Если х 2, то у 0,5 2 2
2
Ответ:
т=2
у 0,5 х 2
х 0
13.
0,5 хy
х х
x 2
2
Проверка (3):
При каких значениях т прямая
y = т не имеет с графиком ни
одной общей точки
1. Упростить выражение
а, если а 0
х 2
а 2
0,5 х ах, если
х а 0 ,50х х 2 х
0,5х х
х 2
х 2
2. Раскрываем модуль по определению
5
у 0,5 х 2
х 0
2
0,5 х , если х 0
0,5 х х
2
0
,
5
x
, если х 0
-2
3. Определить т
Если х 2, то у 0,5 2 2
2
Ответ:
т = -2
т 2
у 0,5 х 2
х 0
14.
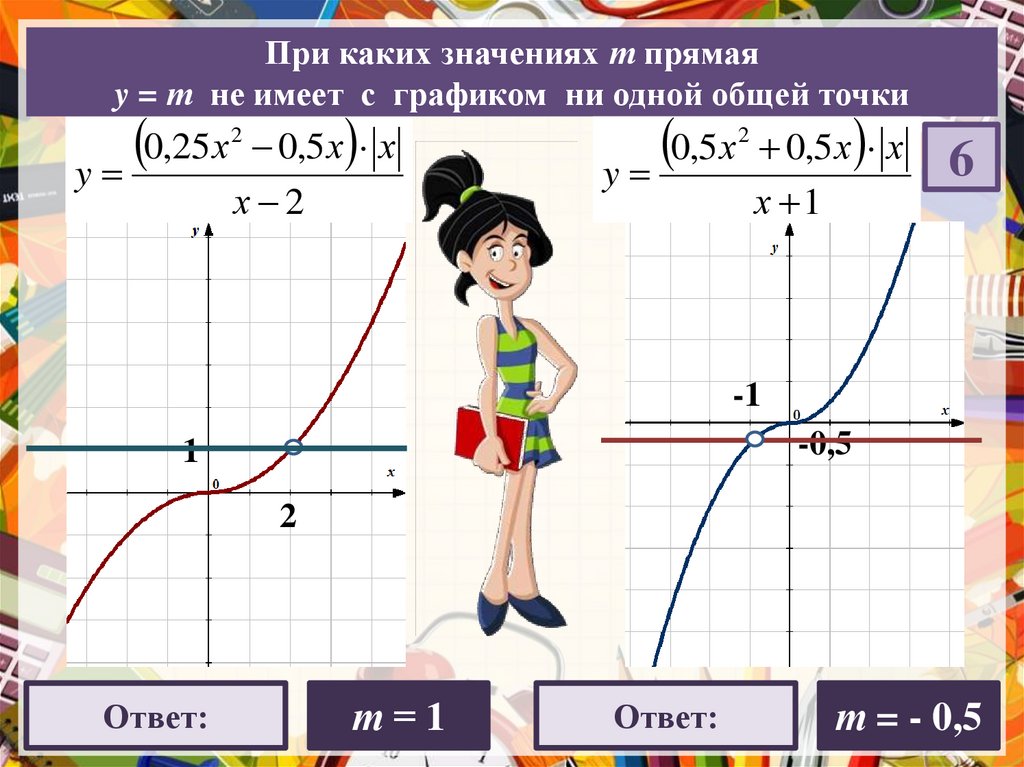
При каких значениях т прямаяy = т не имеет с графиком ни одной общей точки
0,25 х
y
0,5 х х
х 2
2
0,5 х
y
2
0,5 х х
х 1
6
-1
-0,5
1
2
Ответ:
т=1
Ответ:
т = - 0,5
15.
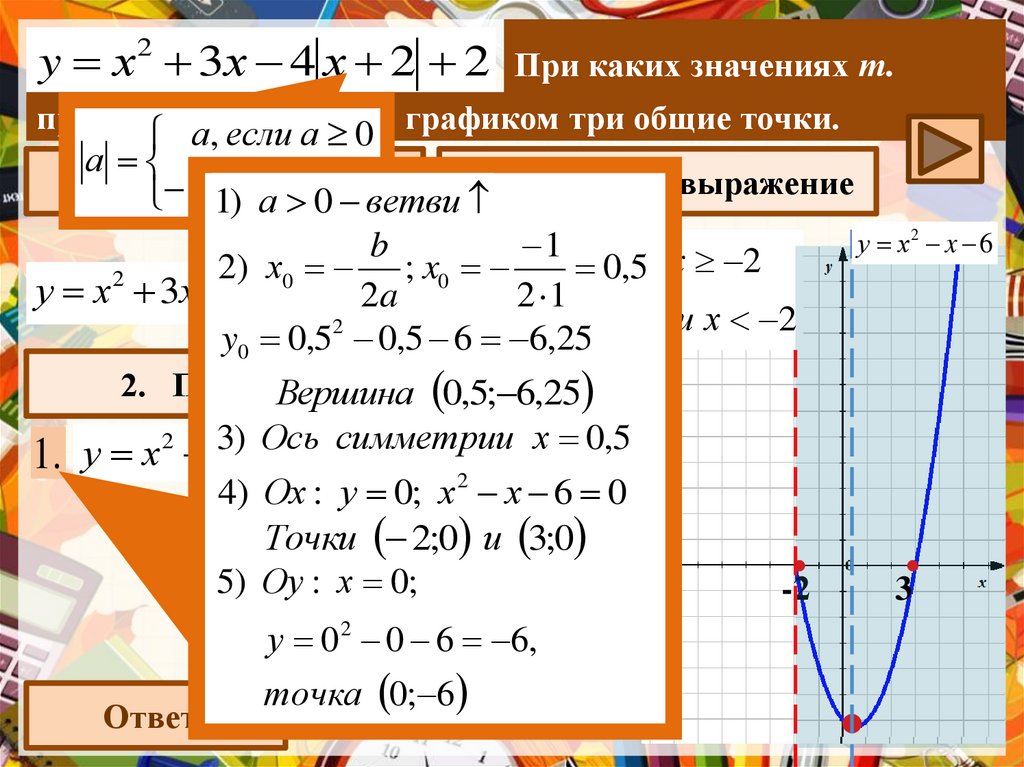
y х 2 3х 4 х 2 2При каких значениях т.
прямая y а=, т
имеет
с графиком три общие точки.
если
а
0
а
Алгоритм
1. Упростить выражение
а 0
а, если(3):
1) а 0 ветви
b х 2 х 16, если х 2
2) х0 ; x 0
0,5
2
у х 3х 4 х 2 22a 2 2 1
х 7 х 10, если х 2
2
y0 0,5 0,5 6 6,25
у х2 x 6
2. Построим
график
0,5; 6,25
Вершина
2
3) Ось
симметрии х 0,5
у
х
x
6
1.
2
4) Ох : у 0; х х 6 0
x2; 0 4и 3;0
Точки3
5) Оу : х 0;
у 02 0 6 6,
Ответ:
точка 0; 6
-2
3
16.
y х 2 3х 4 х 2 2При каких значениях т.
1*
прямая y = т имеет с графиком три общие точки.
Алгоритм (3):
1. Упростить выражение
1) а 0 ветви
2
y
х
7 x 10
2
b
7
х ; x20
2х х 26) ,хесли
3,5
0
у х 2 3х 4 х 2 2a2
2 1
х 2
х 7 х 10
y0 , если
2,25
2. Построим
график
3,5; 2,25
Вершина
2
3) Ось
симметрии х 3,5
у
х
x
6
1.
2
2.
4) Ох : у 0; х 7 х 10 0
y х 2 7 xТочки
10 2;0 и 5;0
5) Оу : х 0; точки нет,
-5
3. Определить т
т.к. х 2
Ответ:
т = -2,25 т = 0
-2
3
17.
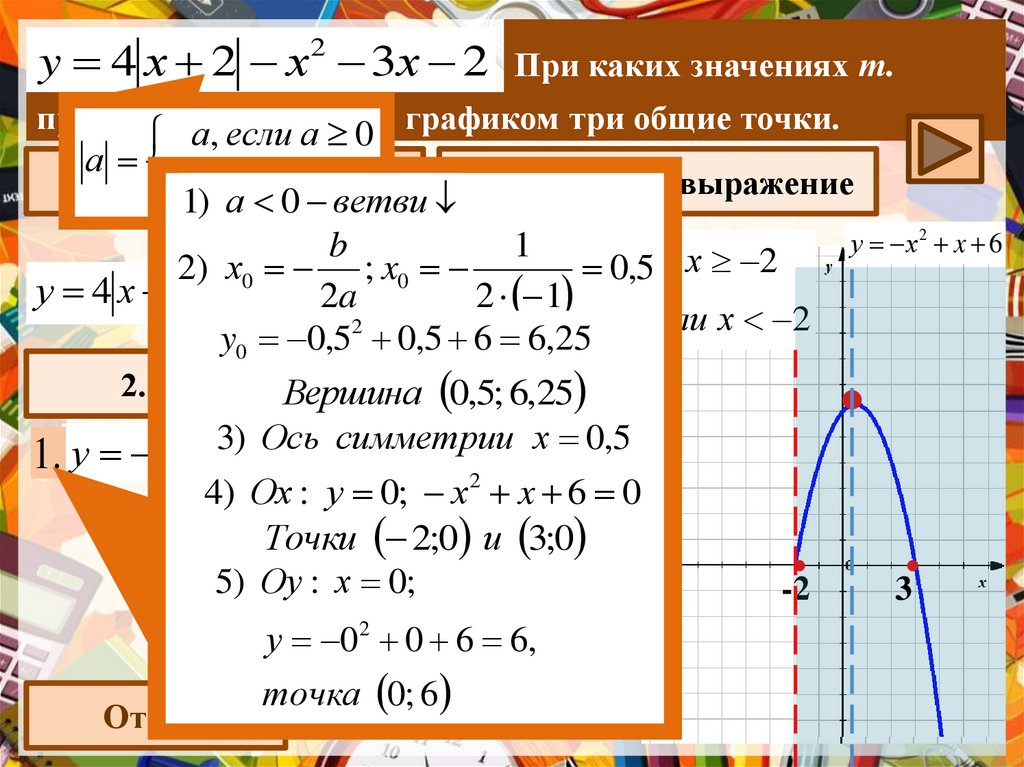
y 4 х 2 х 2 3х 2При каких значениях т.
прямая y а=, т
имеет
с графиком три общие точки.
если
а
0
а
Алгоритм
1. Упростить выражение
а 0
а, если(3):
1) а 0 ветви
2 1
b
х
2) х02 ; x0 х 6 , если
0,5 х 2
у 4 х 2 х 3х2
a 2 22 1
х 7 х 10, если х 2
2
y0 0,5 0 ,5 6 6,25
у х2 x 6
2. Построим
график 0,5; 6,25
Вершина
2 3) Ось симметрии х 0,5
у
х
x 6
1.
4) Ох : у 0; х 2 x 6 0
x2; 0 4и 3;0
Точки3
5) Оу : х 0;
у 02 0 6 6,
Ответ:
точка 0; 6
-2
3
18.
y 4 х 2 x 2 3x 2При каких значениях т.
2*
прямая y = т имеет с графиком три общие точки.
Алгоритм (3):
1. Упростить выражение
1) а 0 ветви
2
b х 2
х
х
6
,
если
2) х0 ; x0 3,5
2
у х 23х 4 х 2 2 a2
, если
х 2
х 7 х y10
2
,
25
0
y х 2 7 x 10
2. Построим
график
3,5; 2,25
Вершина
2 3) Ось симметрии х 3,5
у
х
x 6
1.
4) Ох : у 0; х 2 7 x 10 0
10 2;0 и 5;0
2. y х2 7 xТочки
5) Оу : х 0; точки нет,
-5
3. Определить т
т.к. х 2
Ответ:
т = 2,25
т=0
-2
3
19.
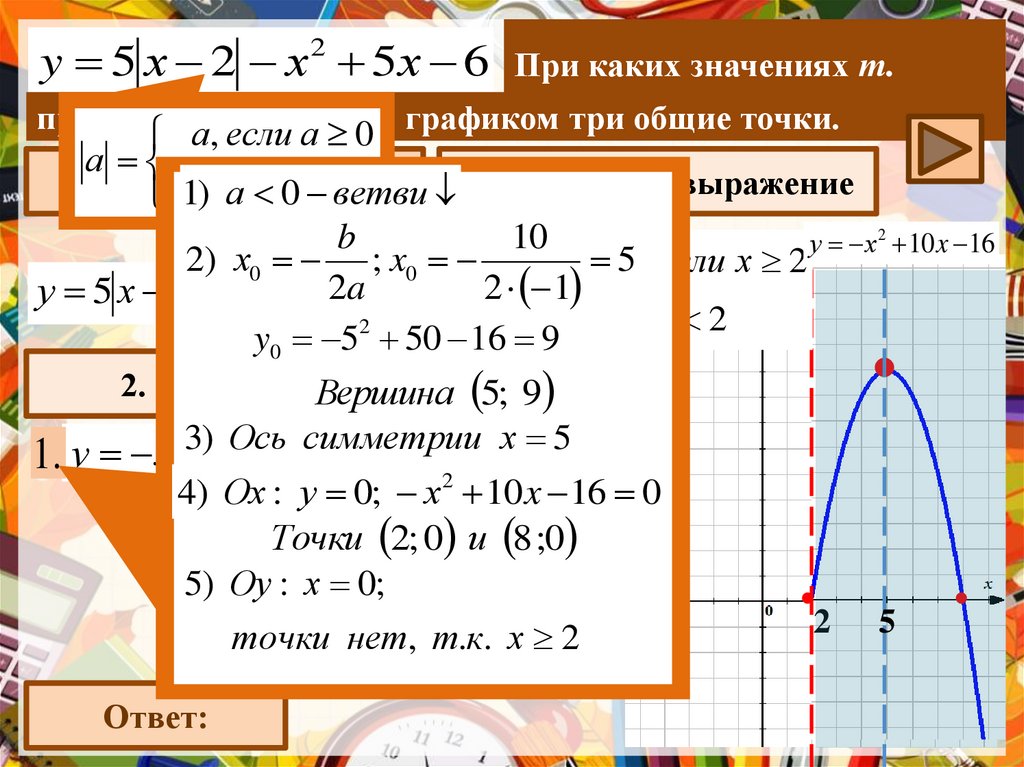
y 5 х 2 х 2 5х 6При каких значениях т.
прямая y а=, т
имеет
с графиком три общие точки.
если
а
0
а
Алгоритм
0
а (3):
0а ветви
1. Упростить выражение
1а), если
b
у х 2 10 x 16
2 10
2) х20 ; x0
5 , если х 2
х 10 х 16
у 5 х 2 х 5х2 a6 22 1
2
х16 49, если х 2
y0 5 50
1.
2. ПостроимВершина
график 5; 9
у х 23 ) xОсь
6 симметрии х 5
4) Ох : у 0; х 2 10 x 16 0
Точки3 2x; 0 4и 8 ;0
5) Оу : х 0;
точки нет, т.к. х 2
Ответ:
2
5
20.
y 5 х 2 x 2 5x 6При каких значениях т.
прямая y = т имеет с графиком три общие точки.
Алгоритм (3):
1. Упростить выражение
1) а 0 ветви
2
b х 2 0
х
10
х
16
,
если
2) 0 ; x0
0
2
у х 23х 4 х 2 2 a2
2
х 4, если
y0 х4 2
1.
2.
y х2 4
2. Построим
график 0; 4
Вершина
у х 2 3)xОсь
6 симметрии ось Оу
4) Ох : у 0; х2 4 0
y х 2 4 Точки 2; 0 и 2; 0
5) Оу : х 0; у 4
3. Определить т
Ответ:
т=4
т=0
-2
2
5
3
21.
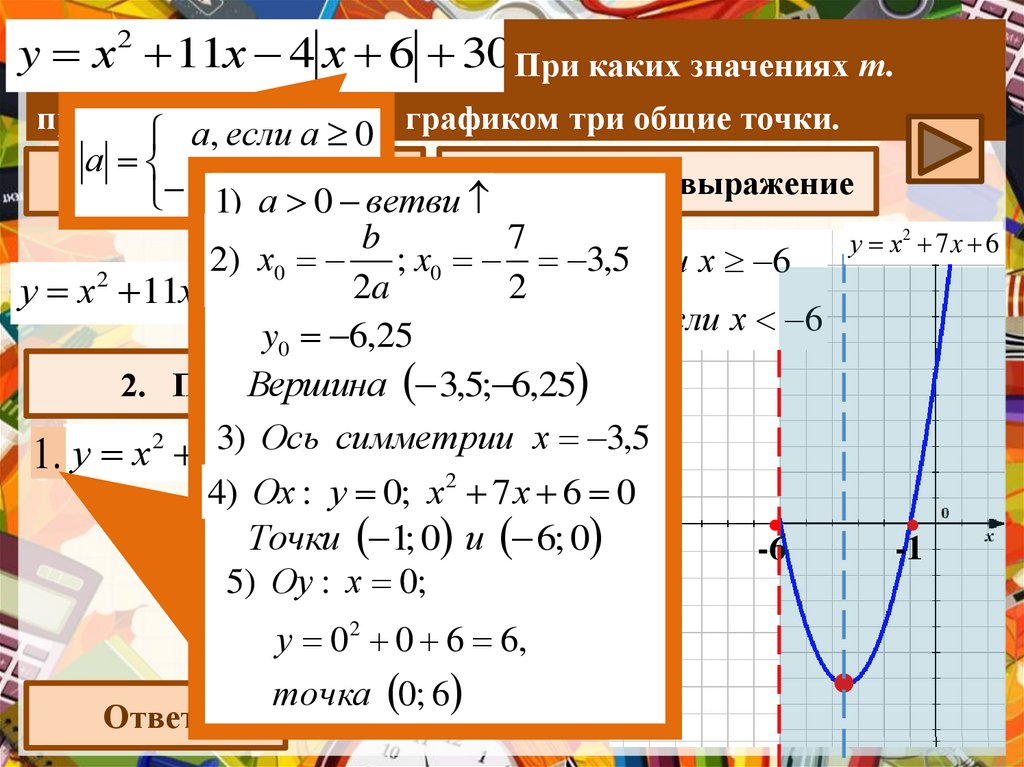
y х 11х 4 х 6 30 При каких значениях т.2
прямая y а=, т
имеет
с графиком три общие точки.
если
а
0
а
Алгоритм
1. Упростить выражение
а 0
а, если(3):
1) а 0 ветви
b
2 7
2) х0 ; x0
х 7
х 36,5если х 6
2
a 2 2
у х 11х 4 х 6 230
y0 6,25 х 15 х 54, если х 6
3,5; 6,25
Вершина
2. Построим
график
у х 2 73x) Ось
6 симметрии х 3,5
1.
4) Ох : у 0; х 2 7 х 6 0
Точки 3 1;x0 4
и 6; 0
5) Оу : х 0;
у 02 0 6 6,
Ответ:
точка 0; 6
-6
у х2 7 x 6
-1
22.
y х2 11х 4 х 6 30 При каких значениях т. 4прямая y = т имеет с графиком три общие точки.
Алгоритм (3):
1. Упростить выражение
1) а 0 ветви
2
b х 6 15
2х 72х) х06 , если
; x0 7,5
у х 2 3х 4 х 22
a2
2
,
если
х 6
х 15 х y54
2
,
25
0
y х 2 15 x 54
2. Построим
график
7,5; 2,25
Вершина
2 3) Ось симметрии х 7,5
у
х
x 6
1.
2
4) Ох : у 0; х 15х 54 0
54 9; 0 и 6; 0
2. y х2 15xТочки
-9
5) Оу : х 0; точки нет,
3. Определить т
т.к. х 6
Ответ:
т = -2,25 т = 0
-6
-1
23.
y х2 8х 4 х 3 15При каких значениях т.
прямая y а=, т
имеет
с графиком три общие точки.
если
а
0
а
Алгоритм
1. Упростить выражение
а 0
а, если(3):
1) а 0 ветви
2 12
b
х
2) х0 ; x0 12 х
27
6 , если х 3
2
у х 8х 4 х 3 215
a 2 2
4 х 93, если х 3
y0 36 12 6 х 27
у х2 12 x 27
2. Построим
график 6; 9
Вершина
2 3) Ось симметрии х 6
1. у х 12 x 27
4) Ох : у 0; х 2 12 х 27 0
Точки3 3x; 0 4и 9; 0
5) Оу : х 0;
точки нет, т.к. х 3
Ответ:
3
9
24.
y х2 8х 4 х 3 15При каких значениях т.
5
прямая y = т имеет с графиком три общие точки.
Алгоритм (3):
1. Упростить выражение
1) а 0 ветви
2
b
4
х
27
,
если
х
3
2х 12
2) 0 ; x0
2
у х 2 3х 4 х 22
a2
2
х 4 х y 03 , если
4 8 х 3 3 1
2; 1
Вершина
2. Построим
график
Ось
х 2
у х 2 3 )12
x симметрии
27
1.
2.
4) Ох : у 0; х 2 4 х 3 0
y х 2 4 xТочки
3 1; 0 и 3; 0
5) Оу : х 0; у 3
3. Определить т
Ответ:
т = -1
т=0
y х2 4 x 3
1
3
9
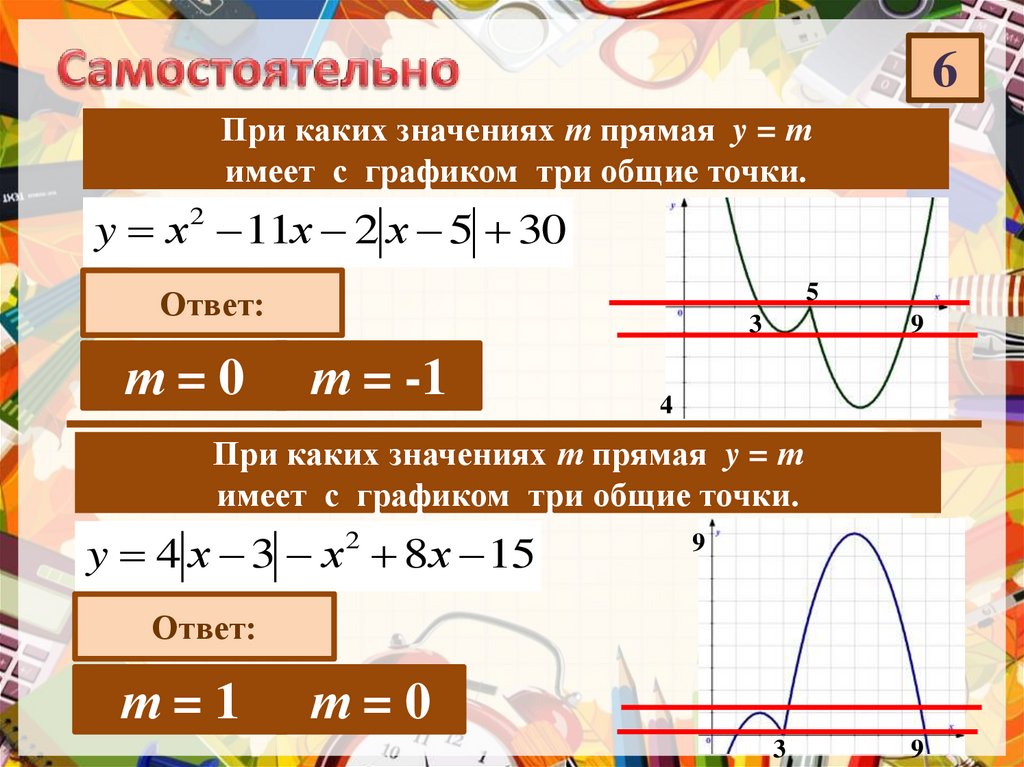
25.
6При каких значениях т прямая y = т
имеет с графиком три общие точки.
y х2 11х 2 х 5 30
5
Ответ:
т=0
3
т = -1
9
4
При каких значениях т прямая y = т
имеет с графиком три общие точки.
y 4 х 3 х2 8х 15
9
Ответ:
т=1
т=0
3
9
26.
1,5 x 1y
2
x 1,5 x
При каких значениях k прямая y = kx
не имеет с графиком общих точек.
1
, если x 0
1
,
5
x
1
x Преобразовать выражение
Алгоритм (2): 1.
y
2
1
x 1,5 x
1 x 0 1
1,5 х 1 1,5 , хесли
2
2
у
x
х х
2
х 1,5 х
х 1 1,5 х
х
3
3
2. Построить график и определить k
1. у kx совпадает с осью Ох
k 0 и/или
-2/3 2/3
2. проходит через точки
y
2 3 2 ; 3
k
;
x
3 2 3 2
Ответ:
k = -2,25; 0; 2,25
1*
х 0
27.
3 x 1y
2
x 3x
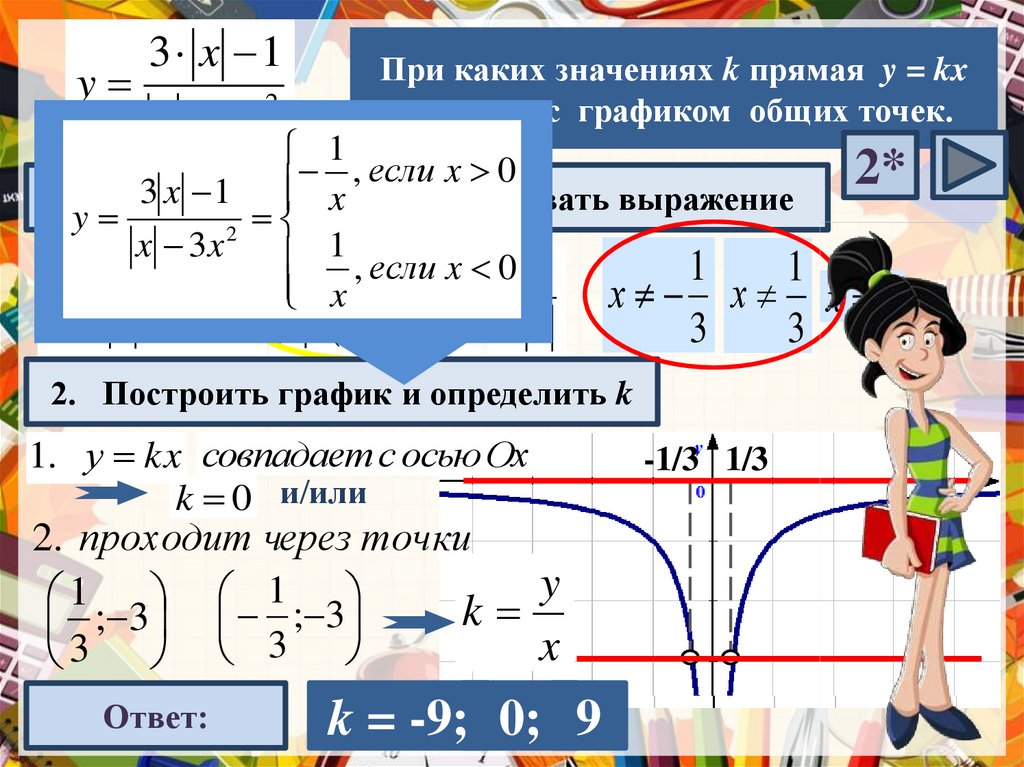
При каких значениях k прямая y = kx
не имеет с графиком общих точек.
1
, если x 0
3
x
1
Алгоритм (2): x1. Преобразовать выражение
y
2
1
x 3x
1 x 0 1
3 х 1 3 х, если
1
1
у
x
х х
2
х 3х
х 1 3 х
х
3
2. Построить график и определить k
1. у kx совпадает с осью Ох
k 0 и/или
2. проходит через точки
y
1
1 ; 3
k
; 3
x
3
3
Ответ:
k = -9; 0; 9
-1/3 1/3
3
2*
х 0
28.
2,5 x 1y
2
x 2,5 x
При каких значениях k прямая y = kx
не имеет с графиком общих точек.
1
, если x 0
2
,
5
x
1
Проверка (2): 1.
x Преобразовать выражение
y
2
1
x 2,5 x
1 x 0 1
2,5 х 1 2,5 , хесли
2
2
у
x
х х
2
х 2,5 х
х 1 2,5 х
х
5
2. Построить график и определить k
1. у kx совпадает с осью Ох
k 0 и/или
-2/5 2/5
2. проходит через точки
y
2 5 2 ; 5
k
;
x
5 2 5 2
Ответ:
k = -6,25; 0; 6,25
5
3
х 0
29.
2 x 1y
2
x 2x
При каких значениях k прямая y = kx
не имеет с графиком общих точек.
1
, если x 0
2
x
1
Проверка (2): x1. Преобразовать выражение
y
2
1
x 2x
1 x 0 1
2 х 1 2 х, если
1
1
у
x
х х
2
х 2х
х 1 2 х
х
2
2. Построить график и определить k
1. у kx совпадает с осью Ох
k 0 и/или
2. проходит через точки
y
1
1 ; 2
k
; 2
x
2
2
Ответ:
k = -4; 0; 4
-1/2 1/2
2
4
х 0
30.
3,5 x 1y
2
x 3,5 x
При каких значениях k прямая y = kx
не имеет с графиком общих точек.
1
, если x 0
3
,
5
x
1
Проверка (2): 1.
x Преобразовать выражение
y
2
1
x 3,5 x
1 x 0 1
3,5 х 1 3,5 , хесли
2
2
у
x
х х
2
х 3,5 х
х 1 3,5 х
х
7
2. Построить график и определить k
1. у kx совпадает с осью Ох
k 0 и/или
-2/7 2/7
2. проходит через точки
y
2 7 2 ; 7
k
;
x
7 2 7 2
Ответ:
k = -12,25; 0; 12,25
7
5
х 0
31.
6При каких значениях k прямая y = kx
не имеет с графиком общих точек.
4 x 1
y
2
x 4x
Ответ:
1. у kx совпадает с осью Ох и/или
2. проходит через точки
k = -16; 0; 16
2 7
;
7 2
2 7
;
7 2
При каких значениях k прямая y = kx
не имеет с графиком общих точек.
1. у kx совпадает с осью Ох и/или
4,5 x 1
y
2. проходит через точки
2
x 4,5 x
Ответ:
k = -20,25; 0; 20,25
2 9
;
9 2
2 9
;
9 2
32.
Фон для слайдовСтаршеклассники
Открытый банк заданий ФИПИ
























 Математика
Математика








