Похожие презентации:
Графики линейной функции, содержащей модуль
1. Графики линейной функции, содержащей модуль.
2. I. Графики функций вида y = |kx+b|
Для построения графика функции y=|kx+b|надо сохранить ту часть графика функции
y=kx+b, точки которой находятся на оси Ох
или выше этой оси, и симметрично отразить
относительно оси Ох ту часть графика
функции y=kx+b, которая расположена
ниже оси Ох.
3. Построение графика
y1
у х 3
2
1. Построим
график функции
1
у х 3
2
х
0
4
у
-3
-1
2. Выполним
необходимые
преобразования
графика линейной
функции
0
x
4. II. Графики функций вида y= k|x|+b
Для построения графика функцииy= k|x|+b надо сохранить ту часть
графика функции y=kx+b, точки которой
находятся на оси Оу или справа от неё, и
симметрично отразить эту часть
относительно оси Оу.
5. Построение графика функции
у 3 x 2y
1. Построить
график функции
у 3х 2
х
0
2
у
-2
4
x
0
2. Выполним
необходимые
преобразования
графика линейной
функции
6. Устная работа
y3
2
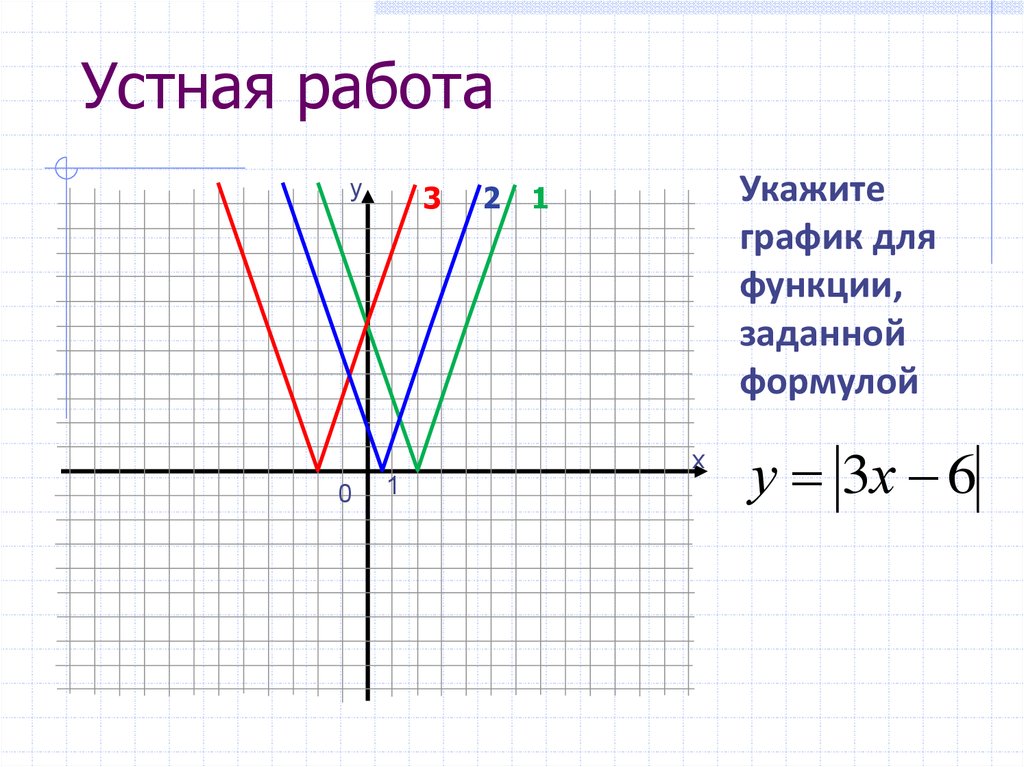
Укажите
график для
функции,
заданной
формулой
1
x
0
1
у 3х 6
7. Устная работа
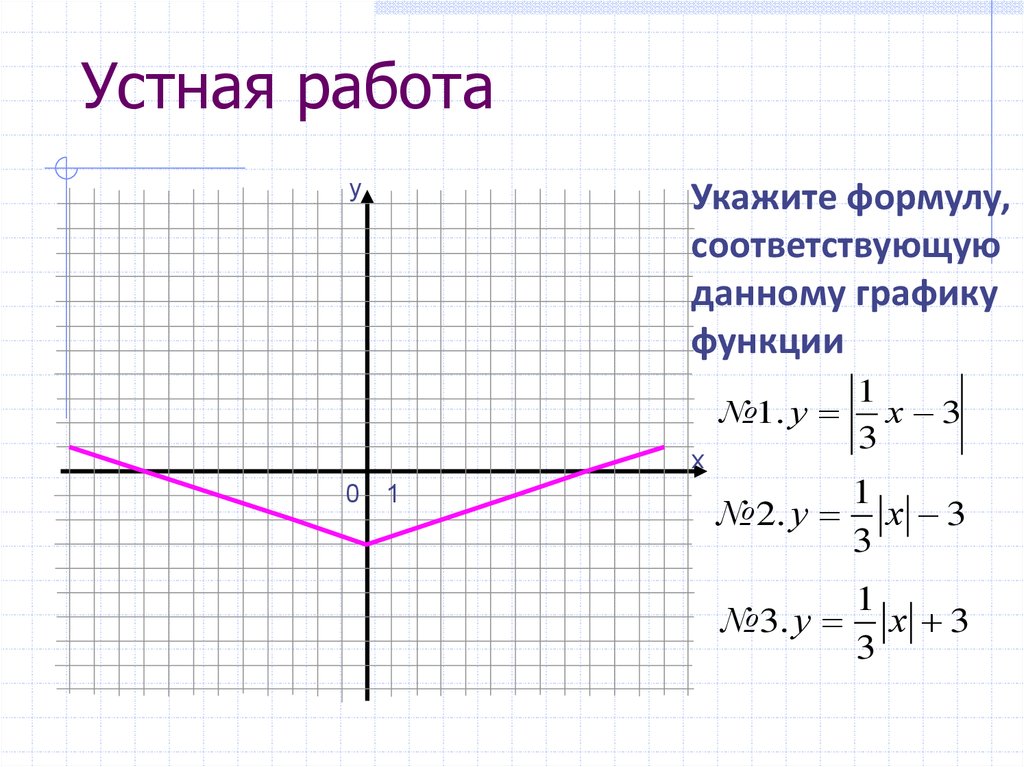
yУкажите формулу,
соответствующую
данному графику
функции
x
0
1
1
№1. у х 3
3
1
№ 2. у х 3
3
№3. у
1
х 3
3
8. Устная работа
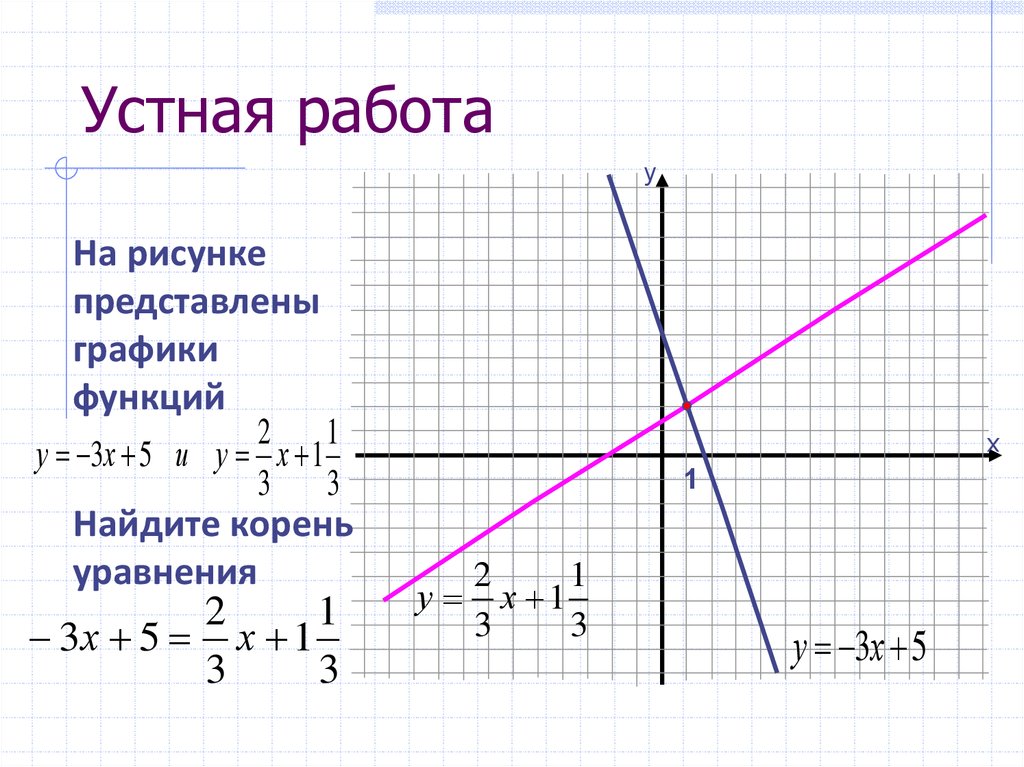
yНа рисунке
представлены
графики
функций
2
1
у 3х 5 и у х 1
3
3
Найдите корень
уравнения
2
1
3х 5 х 1
3
3
x
1
2
1
у х 1
3
3
у 3х 5
9. Устная работа
y3
2
Укажите
график для
функции,
заданной
формулой
1
x
0
1
у 3х 6
10. Устная работа
yУкажите формулу,
соответствующую
данному графику
функции
x
0
1
1
№1. у х 3
3
1
№ 2. у х 3
3
№3. у
1
х 3
3
11. Устная работа
yНа рисунке
представлены
графики
функций
2
1
у 3х 5 и у х 1
3
3
Найдите корень
уравнения
2
1
3х 5 х 1
3
3
x
1
2
1
у х 1
3
3
у 3х 5
12. Построение графика функции
1у
х 2
1
2
1
1. у х 2
2. у х 2
2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
Первый вариант выполняет построения №1, второй вариант - №2.
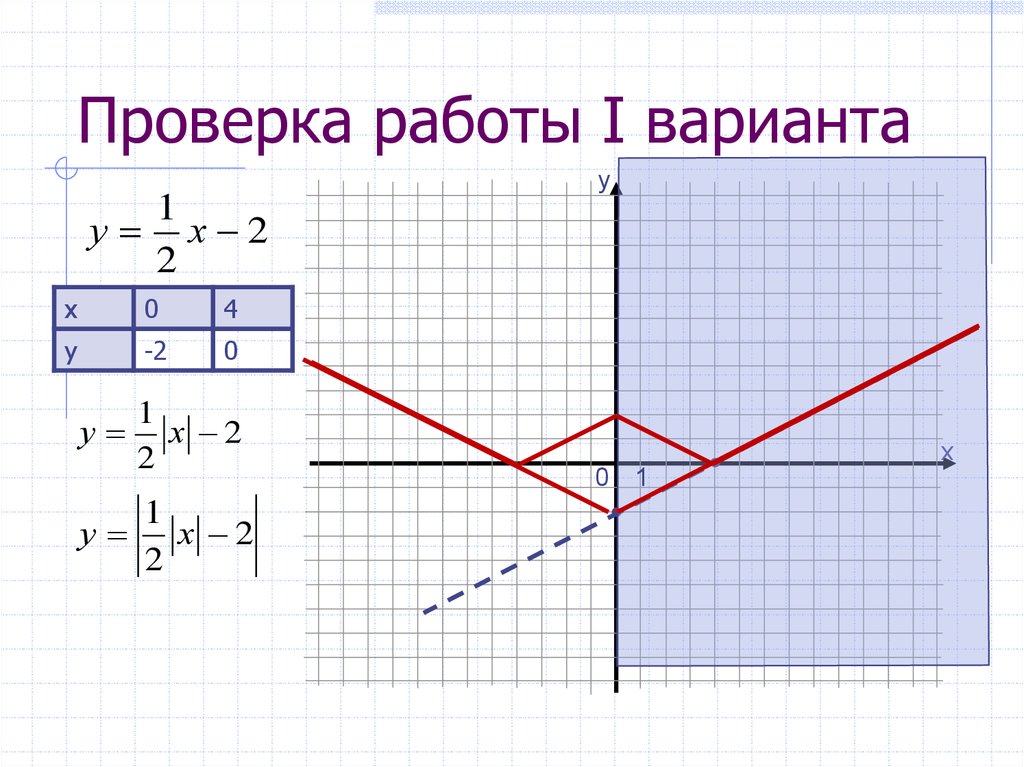
13. Проверка работы I варианта
1у х 2
2
х
0
4
у
-2
0
у
1
х 2
2
1
у х 2
2
y
x
0
1
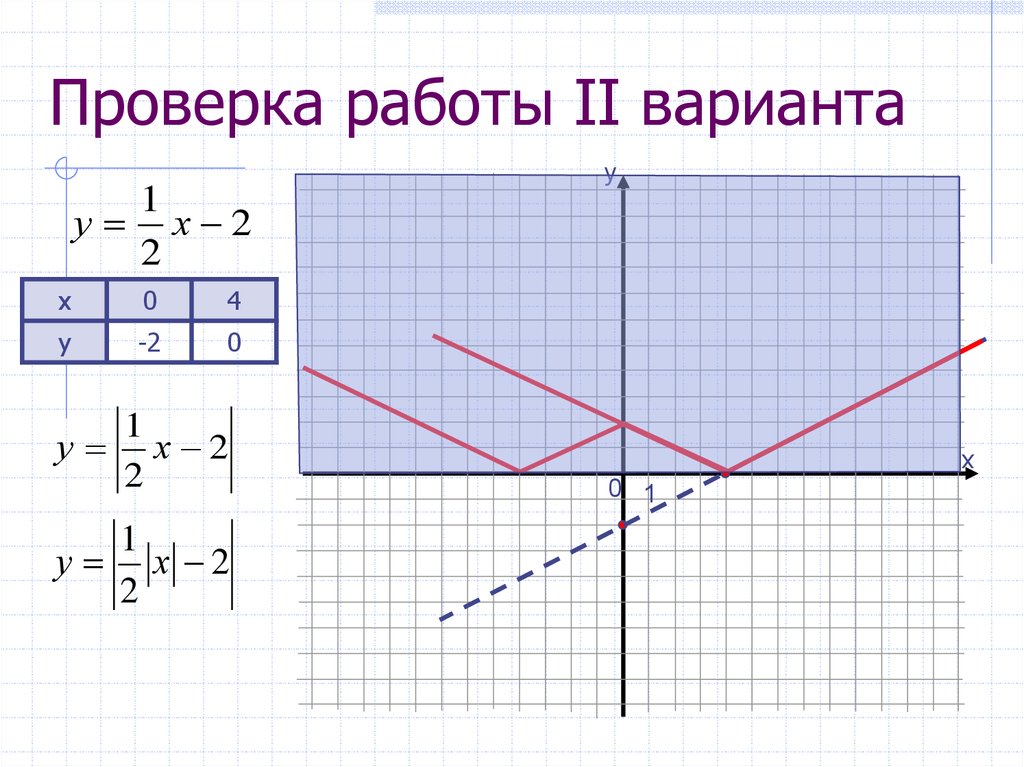
14. Проверка работы II варианта
1у х 2
2
х
0
4
у
-2
0
1
у х 2
2
1
у х 2
2
y
x
0 1
15.
Исследуйте число решенийу 2 х 2 4х 24
2
b
уравнения
y
у 2х 4 2
y b
у 2х 4 2
Горизонтальная
прямая, проходящая
через точку с
ординатой b.
Ответ: если b<0, то уравнение не имеет корней; если
b=0, то уравнение имеет два корня; если 0<b<2, то
уравнение имеет четыре корня; если b=2, то
уравнение
имеет
три корня;
если
то
уравнение
Если
Если
Если
0<b<2,
b>2
b<0,
уравнение
то
то
уравнение
уравнение
имеет
корней
имеет
дваb>2,
корня
четыре
не
имеет.
корня.
Если
Если
b=2,
b=0,
то
то
уравнение
уравнение
имеет
имеет
три
два
корня.
корня.
имеет два корня.
x
16. При каком значении b уравнение имеет единственное решение
При каком значении b уравнение 3х 6 2 х bимеет единственное решение
1. у 3х 6
y
2. у 2 х b
Ответ: при
b>-3
исходное
уравнение
имеет
единственно
е решение.
x
-3
17.
18. Домашнее задание
у 2х 419.
y1
0
1
x














 Математика
Математика








