Термодинамические процессы с идеальным газом

1. Термодинамические процессы с идеальным газом

2. Основные цели изучения термодинамических процессов

Установить уравнение процесса, т.е.
связь между термодинамическими
параметрами;
Определить работу, совершаемую
газом;
Количество теплоты, сообщаемое газу
или отводимое от него в процессе.

3. Основные изменения состояния, которым может подвергаться газ:

Изобарный процесс, протекающий при
постоянном давлении;
Изохорный процесс, протекающий при
постоянном объеме;
Изотермический процесс, протекающий при
постоянной температуре;
Адиабатный или изоэнтропийный (т.е.
проходящий при постоянной энтропии) процесс, в
ходе которого отсутствует теплообмен с внешней
средой;
Политропный процесс, в ходе которого
изменяются все параметры: давление, объем,
температура и происходит обмен теплом с
внешней средой

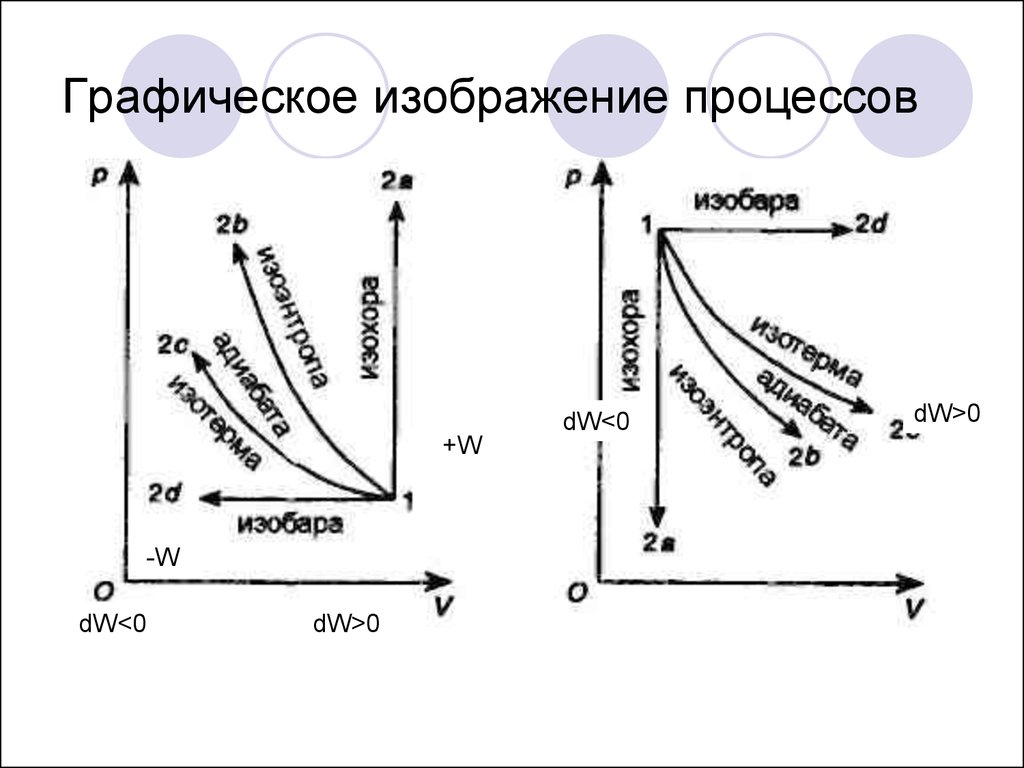
4. Графическое изображение процессов

dW<0
+W
-W
dW<0
dW>0
dW>0

5.

-W
+W
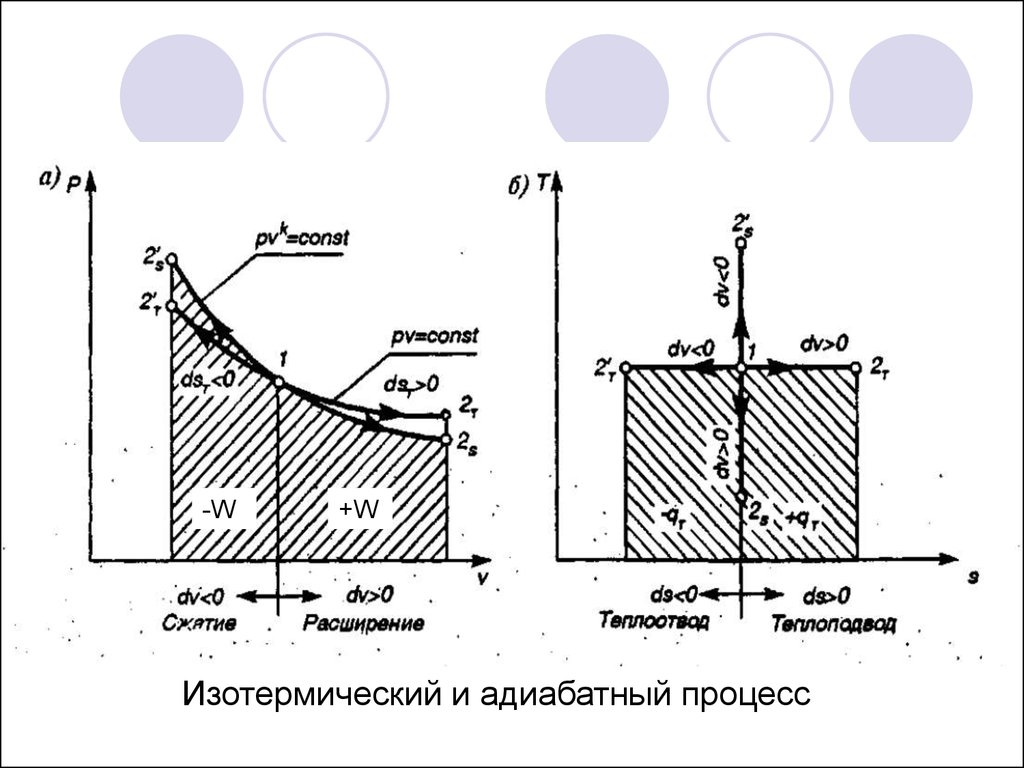
Изотермический и адиабатный процесс

6.

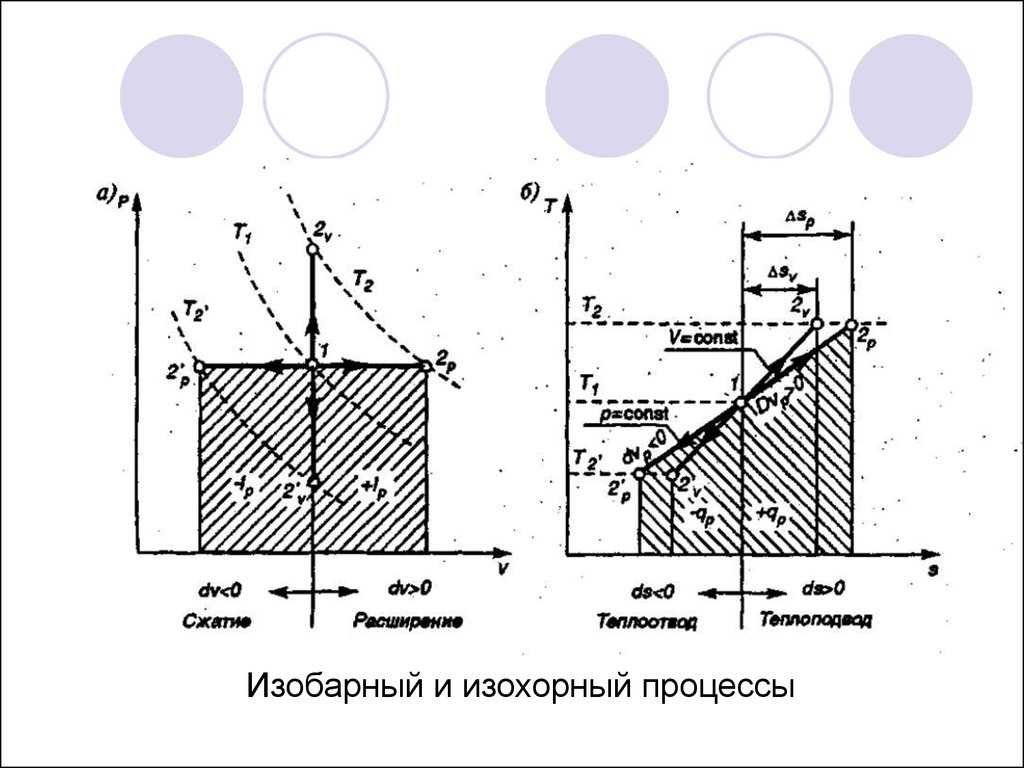
Изобарный и изохорный процессы

7.

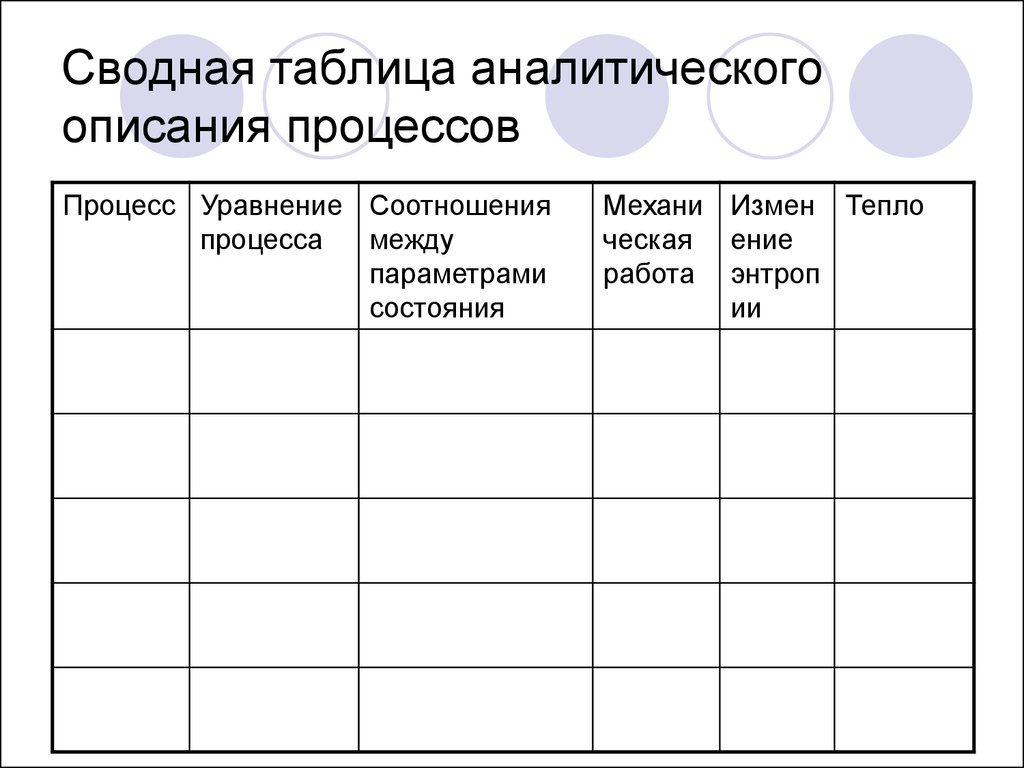
Политропные процессы

8. Сводная таблица аналитического описания процессов

Процесс Уравнение Соотношения
процесса
между
параметрами
состояния
Механи Измен Тепло
ческая ение
работа энтроп
ии

9. Изохорный процесс

V=const
Уравнение Шарля
Механическая работа W=0
Изменение удельной
энтропии
Удельное тепло
приведенное к 1 кг
вещества
p1 p 2
T1 T2
T2
s v c v ln
T1
q c v (T2 T1 )

10. Изохорный процесс

Тепло М кг вещества
Q М c vm (T2 T1 )

11. Изобарный процесс

P=const
Закон Гей-Люссака
Удельная
механическая w
работа 1 кг газа
Изменение энтропии
1 кг газа
Удельная теплота
1 кг газа
v1 v 2
T1 T2
V1 T1
V2 T2
p( v 2 v1 ) R (T2 T1 )
T2
s p c p ln
T1
q c pm (T2 T1 )

12.

Механическая
работа М кг газа
W p M( v 2 v1 ) R M(T2 T1 ) p(V2 V1 )
Изменение энтропии
М кг газа
Тепло М кг газа
T2
Sp M c p ln
T1
Q M c p (T2 T1 )

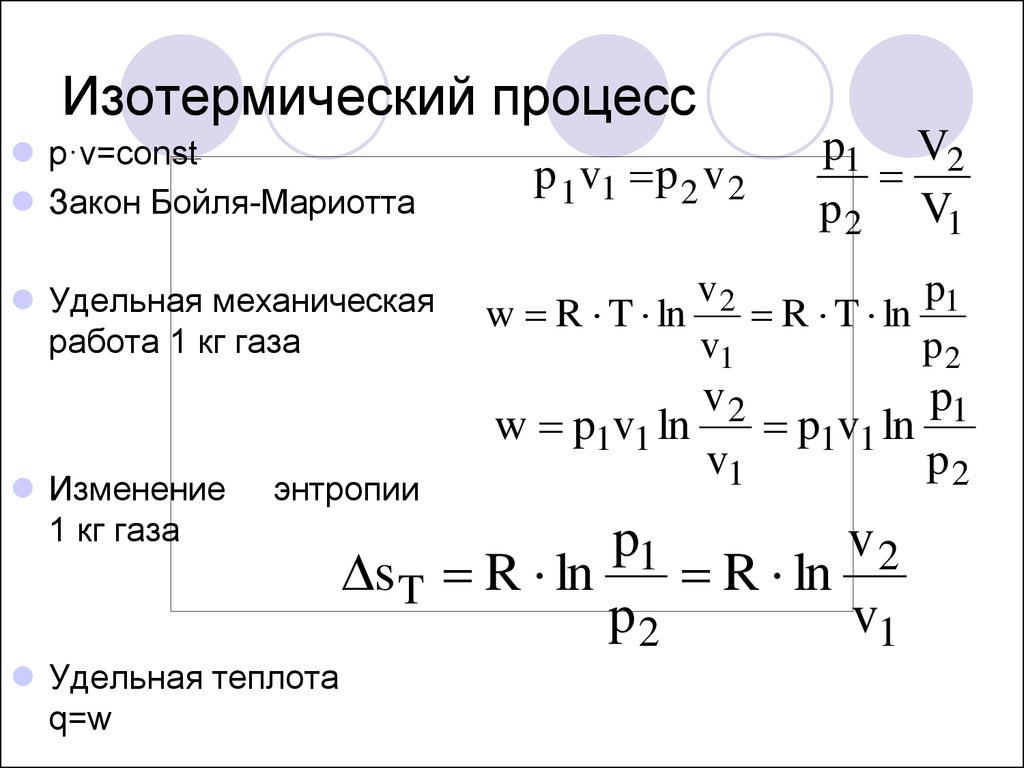
13. Изотермический процесс

p·v=const
Закон Бойля-Мариотта
Удельная механическая
работа 1 кг газа
Изменение
1 кг газа
энтропии
Удельная теплота
q=w
p 1 v1 p 2 v 2
p1 V2
p 2 V1
v2
p1
w R T ln
R T ln
v1
p2
v2
p1
w p1v1 ln
p1v1 ln
v1
p2
p1
v2
s T R ln
R ln
p2
v1

14. Изотермический процесс

v2
p1
W M R T ln
M R T ln
Механическая
v1
p2
работа М кг
газа
Изменение
энтропии М кг
газа
v2
p1
W p1V1 ln ; W p1V1 ln
v1
p2
p1
v2
ST M R ln
M R ln
p2
v1
Тепло М кг газа
Q=W

15. Адиабатный процесс

p·vk=const
Уравнение
Пуассона,
где
k=cp/cv
Зависимости между
начальными и
конечными
параметрами
процесса
k
k
p1v1 p2 v2
k 1
T1v1
k 1
T2 v2
p 2 v1
p1 v 2
k
T2 v1
T1 v 2
k 1
T2 p 2 k
T1
p
1
k 1

16. Адиабатный процесс

Механическая работа
для 1 кг газа
(p1v1 p 2 v 2 ) R (T1 T2 )
w
k 1
k 1
k 1
p k
v k 1
2
p1v1 1
p v 1 1
1 1
v
p1
2
w
k 1
k 1
Изменение энтропии 1 кг
газа s=0
Удельная теплота 1 кг
газа q=0

17. Адиабатный процесс

Механическая
работа М кг
(p1V1 p 2 V2 ) R M(T1 T2 )
W
k 1
k 1
k 1
p k
k 1
p1V1 1 2
p V 1 V1
1 1
V
p1
2
W
k 1
k 1

18. Политропный процесс

Соотношение
между
термодинами
ческими
параметрами
p1v1n p 2 v n2 ;
n 1
n
p1
T2
T 1 p2
v1
v
2
n 1
n
p1
T2 T1
p
2
n
n 1
;
1
n
v2 v2
p1
p1
;
;
p2
v1 v1
p2

19. Политропный процесс

Механическая работа
для 1 кг газа
k 1
w
q
k n
(p1v1 p 2 v 2 ) R (T1 T2 )
w
n 1
n 1
n 1
p n
n 1
p1v1 1 2
p v 1 v1
1 1
v
p1
2
w
n 1
n 1

20. Политропный процесс

Удельная энтропия
для 1 кг газа
n k T2
s c v
ln
n 1 T1
Удельная теплота для
1 кг газа
n k
q cv
(T2 T1)
n 1

21. ПОЛИТРОПНЫЙ ПРОЦЕСС

Работа М кг
газа
p1v1 p 2 v 2 p1V1 p 2 V2 M R (T1 T2 )
W M
n 1
n 1
n 1
n 1
n 1
p1V1 V1 p1V1 p 2 n k 1
W
1
1
Q
n 1 V2 n 1 p1
k n

22. ПОЛИТРОПНЫЙ ПРОЦЕСС

Энтропия
М кг газа
n k T2
S M c v
ln
n 1 T1
Теплота М кг газа
n k
Q M cv
(T2 T1 ) M c(T2 T1 )
n 1