Похожие презентации:
Электротехнические устройства и законы постоянного тока
1.
Электротехнические устройства и законы постоянного токаЭлектротехнические генерирующие и приемные устройства
Источники питания цепи постоянного тока — это гальванические элементы,
электрические аккумуляторы, электромеханические генераторы, термоэлектрические
генераторы, фотоэлементы и др.
Все источники питания имеют внутреннее сопротивление Rвт, значение которого
невелико по сравнению с сопротивлением других элементов электрической цепи.
Электроприемниками постоянного тока являются электродвигатели, преобразующие
электрическую энергию в механическую, нагревательные и осветительные приборы,
электролизные установки и др. Все электроприемники характеризуются электрическими
параметрами, среди которых основные — напряжение и мощность. Для нормальной
работы электроприемника на его зажимах необходимо поддерживать номинальное
напряжение Uном (для приемников постоянного Uном = 27, 110, 220, 440 В, а также 6, 12, 24,
36 В).
2.
Электрические цепи постоянного токаЭлектрической цепью называется совокупность устройств и объектов, образующих
путь для электрического тока, электромагнитные процессы в которых могут быть описаны
с помощью понятий об электродвижущей силе, токе и напряжении.
В электрической цепи постоянного тока могут действовать как постоянные токи, т. е.
такие, значение и направление которых в любой момент времени остаются неизменными,
так и токи, направление которых остается постоянным, а значение изменяется во времени
произвольно или по какому-либо закону (такие токи нельзя назвать строго постоянными).
Под цепями постоянного тока в современной технике подразумевают цепи, в которых
ток не меняет своего направления, т. е. полярность источников ЭДС. в которых постоянна.
Электрическая цепь состоит из отдельных устройств или элементов, которые по
назначению можно подразделить на три группы:
1. Элементы, предназначенные для генерирования (выработки) электроэнергии
(источники питания или источники ЭДС).
2. Элементы, преобразующие электроэнергию в другие виды энергии (механическую,
тепловую, световую, химическую и т. д.). Эти элементы называются приемниками
электрической энергии, или нагрузкой.
3. Элементы, предназначенные для передачи электроэнергии от источника питания к
электроприемнику (провода, устройства, обеспечивающие уровень и качество напряжения,
и др.).
3.
Электрическая цепь, электрическое сопротивление участков которой не зависит отзначений и направлений токов и напряжений в цепи, называется линейной электрической
цепью.
Такая цепь состоит только из линейных элементов, а ее состояние описывается
линейными алгебраическими уравнениями. В противном случае цепь называется
нелинейной и описывается более сложными математическими уравнениями.
Для расчета и анализа работы электрической цепи, состоящей из любого количества
различных элементов, удобно эту цепь представить графически. Графическое изображение
электрической цепи, содержащее условные обозначения ее элементов и показывающее
соединения этих элементов, называется схемой электрической цепи. Простейшая схема
электрической цепи, состоящая из источника ЭДС (Е) и резистора сопротивлением (R),
изображена на рис. 1, а.
а — простейшей одноконтурной
4.
Участок электрической цепи, вдоль которого протекает один и тот же ток, называетсяветвью. Место соединения ветвей электрической цепи называется узлом.
На электрических схемах узел обозначают точкой (рис. 1, б)).
Иногда несколько геометрических точек, соединенных проводниками, сопротивление
которых принимают равным нулю (c — d), образуют один узел (рис. 2.1, б), узел с. Таким
образом, каждая ветвь соединяет два соседних узла электрической схемы.
Число ветвей схемы принято обозначать р, а число узлов — q.
Электрическая цепь, изображенная на схеме рис. 1, б), имеет число ветвей р = 5 и
число узлов q = 3 (а, b, с).
Любой замкнутый путь, проходящий по нескольким ветвям, называют контуром
электрической цепи. Простейшая электрическая цепь имеет одноконтурную схему (рис. 1,
а)), сложные электрические цепи — несколько контуров (рис. 1, б)).
б — многоконтурной (p = 5, q = 3)
5.
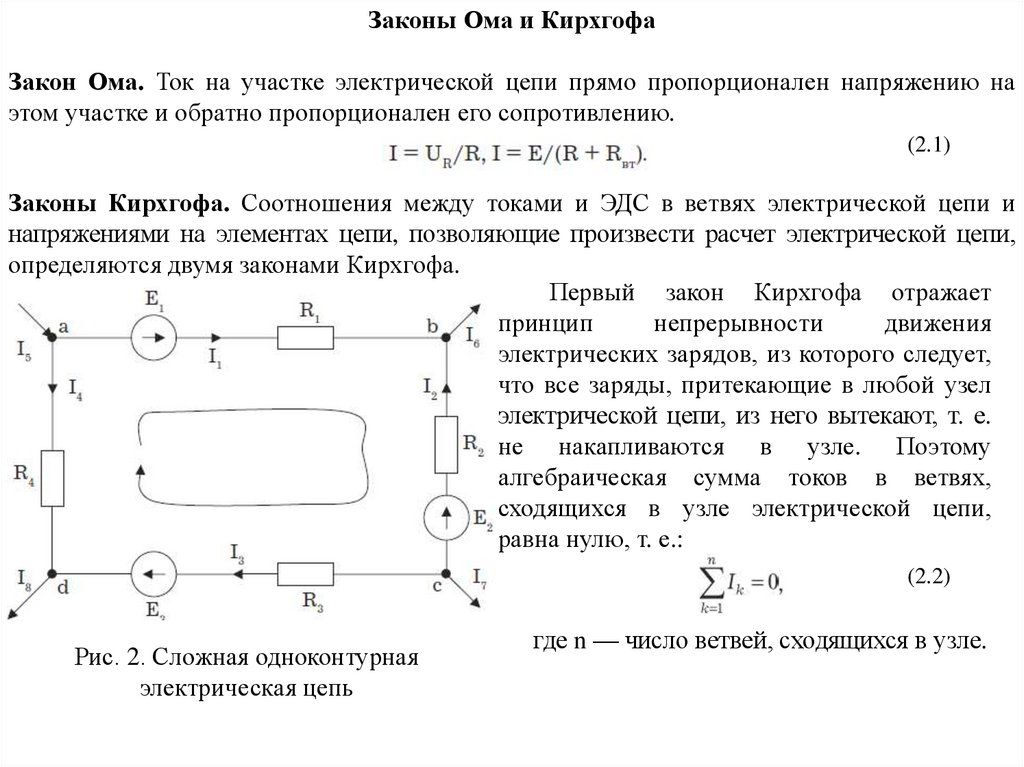
Законы Ома и КирхгофаЗакон Ома. Ток на участке электрической цепи прямо пропорционален напряжению на
этом участке и обратно пропорционален его сопротивлению.
(2.1)
Законы Кирхгофа. Соотношения между токами и ЭДС в ветвях электрической цепи и
напряжениями на элементах цепи, позволяющие произвести расчет электрической цепи,
определяются двумя законами Кирхгофа.
Первый закон Кирхгофа отражает
принцип
непрерывности
движения
электрических зарядов, из которого следует,
что все заряды, притекающие в любой узел
электрической цепи, из него вытекают, т. е.
не накапливаются в узле. Поэтому
алгебраическая сумма токов в ветвях,
сходящихся в узле электрической цепи,
равна нулю, т. е.:
(2.2)
Рис. 2. Сложная одноконтурная
электрическая цепь
где n — число ветвей, сходящихся в узле.
6.
До написания уравнения (2.2) необходимо задать условные положительныенаправления токов в ветвях, обозначив эти направления на схеме стрелками. В уравнении
(2.2) токи, направленные к узлу, записывают с одним знаком (например, с плюсом), а токи,
направленные от узла, — с противоположным (с минусом). Таким образом, для узла b
схемы (рис. 1.б)) уравнение по первому закону Кирхгофа будет иметь вид
Первый закон Кирхгофа может быть сформулирован
притекающих в узел, равна сумме токов, вытекающих из узла.
Тогда уравнение для узла b (рис. 1, б)) будет записано так:
иначе:
сумма
токов,
7.
Второй закон Кирхгофа определяет,что изменение потенциала во всех
элементах контура в сумме равно нулю.
Это значит, что при обходе контура abcda
электрической цепи, показанной на рис. 2,
в силу того, что потенциал точки а один и
тот же, общее изменение потенциала в
контуре равно нулю. Из этого следует, что
алгебраическая сумма ЭДС в любом
контуре электрической цепи постоянного
тока равна алгебраической сумме падений
напряжений на всех элементах, входящих в
этот контур, т. е.
(2.3)
где n — число источников ЭДС в контуре;
m — число элементов (число ветвей) с сопротивлением Rk в контуре.
При составлении уравнений по второму закону Кирхгофа предварительно задают
условные положительные направления токов во всех ветвях электрической цепи и для
каждого контура выбирают направление обхода. Если при этом направление ЭДС
совпадает с направлением обхода контура, то такую ЭДС берут сo знаком плюс, если не
совпадает — со знаком минус. Падения напряжений берут со знаком плюс, если
положительное направление тока в данном элементе цепи совпадает с направлением
обхода контура, и со знаком минус — если такого совпадения нет.
8.
Для контура abcda, сопротивленияветвей которого включают в себя и
внутренние сопротивления источников ЭДС,
уравнение (2.3) принимает вид
Используя второй закон Кирхгофа, можно определять
разность потенциалов (напряжение) между любыми двумя
точками электрической цепи.
Для одноконтурной схемы (рис. 1, а)) в соответствии с
уравнением (2.3) можно записать
Е = R · I = UR.
Но вместо ЭДС Е при обходе контура по направлению тока можно взять напряжение
на зажимах источника ЭДС, которое направлено противоположно направлению обхода
контура, в результате чего получим
UR − U = 0 или U = UR.
Следовательно, второй закон Кирхгофа можно cформулировать в таком виде: сумма
падений напряжений на всех элементах контура, включая источники ЭДС, равна нулю, т. е.
9.
Если в ветви имеется n последовательно соединенных элементов с сопротивлениемk-го элемента Rk, то
т. е. падение напряжения на участке цепи или напряжение между зажимами ветви U,
состоящей из последовательно соединенных элементов, равно сумме падений напряжений
на этих элементах.








 Физика
Физика








