Мастер-класс «Решение задач по геометрии при подготовке к ОГЭ»

1.

Муниципальное бюджетное общеобразовательное учреждение
«средняя общеобразовательная школа имени М.И.Калинина»
муниципального образования «город Бугуруслан»
Мастер-класс
«Решение задач по геометрии
при подготовке к ОГЭ»
Учитель математики Маркова Т.А.

2.

Геометрические задачи на доказательство
Окружности и их элементы
Треугольники и их элементы
Четырехугольники и их элементы

3.

Задача №24
Баллы
Содержание критерия
2
1
Доказательство верное, все шаги обоснованны
Доказательство в целом верное, но содержит неточности
0
Решение не соответствует ни одному из критериев,
перечисленных выше
Максимальный бал
2

4.

Окружности и их элементы
Теоретический материал необходимый
для решения задач:
понятие окружности, круга и их элементов;
взаимное расположение прямой и окружности;
свойства хорд окружности;
касательные и секущие к окружности, свойства;
углы в окружности, свойства вписанных углов;
взаимное расположение двух окружностей, общие
касательные двух окружностей.

5.

В окружности с центром О проведены две хорды АВ и СD так,
что центральные углы АОВ и СОD равны. На эти хорды
опущены перпендикуляры ОК и ОL. Докажите, что ОК и ОL
равны.
С чего
начинается
решение
любой этой
задачи?
Что
необходимо
знать
для решения
задачи?
с чертежа
как строить окружность
понятие центрального угла и радиуса
окружности
свойства дуг и хорд окружности
признаки равенства треугольников

6.

В окружности с центром О проведены две хорды АВ и СD так,
что центральные углы АОВ и СОD равны. На эти хорды
опущены перпендикуляры ОК и ОL. Докажите, что ОК и ОL
равны.
Из чего будет следовать равенство перпендикуляров?
из равенства треугольников
Как доказать, что треугольники
равны?
2 способа ответа

7.

В окружности с центром О проведены две хорды АВ и СD так,
что центральные углы АОВ и СОD равны. На эти хорды
опущены перпендикуляры ОК и ОL. Докажите, что ОК и ОL
равны.
по двум сторонам и углу между
ними или
по трем сторонам (здесь
вспоминаем свойство дуг и хорд
окружности)

8.

В окружности с центром О проведены две хорды АВ и СD так,
что центральные углы АОВ и СОD равны. На эти хорды
опущены перпендикуляры ОК и ОL. Докажите, что ОК и ОL
равны.
высоты ОК и ОL равны как
соответствующие элементы
равных треугольников

9.

Задача для самостоятельного решения
В окружности с центром О проведены две равные хорды
КL и МN. На эти хорды опущены перпендикуляры ОН и
ОS. Докажите, что ОН и OS равны.

10.

Докажите, что угол между касательной и хордой,
имеющими общую точку на окружности, равна половине
градусной меры дуги, заключённой между его сторонами.
сделаем чертеж к задаче
Доказать:
Какой теоретический материал необходим
для решения данной задачи

11.

Докажите, что угол между касательной и хордой,
имеющими общую точку на окружности, равна половине
градусной меры дуги, заключённой между его сторонами.
Какой теоретический материал необходим
для решения данной задачи
признак касательной
градусная мера центрального угла
свойства равнобедренного
треугольника, сумма углов треугольника

12.

Докажите, что угол между касательной и хордой,
имеющими общую точку на окружности, равна половине
градусной меры дуги, заключённой между его сторонами.
1. по признаку касательной
2) пусть
Чему
Какойон
эторавен?
угол?
центральный
(центральный угол равен дуге на
которую опирается)
тогда

13.

Докажите, что угол между касательной и хордой,
имеющими общую точку на окружности, равна половине
градусной меры дуги, заключённой между его сторонами.
3. Что можно сказать о Δ ВОС?
он равнобедренный
Перечислите свойства равнобедренного
треугольника
Какой угол можно найти и как?

14.

Докажите, что угол между касательной и хордой,
имеющими общую точку на окружности, равна половине
градусной меры дуги, заключённой между его сторонами.
4. т.к.
, то

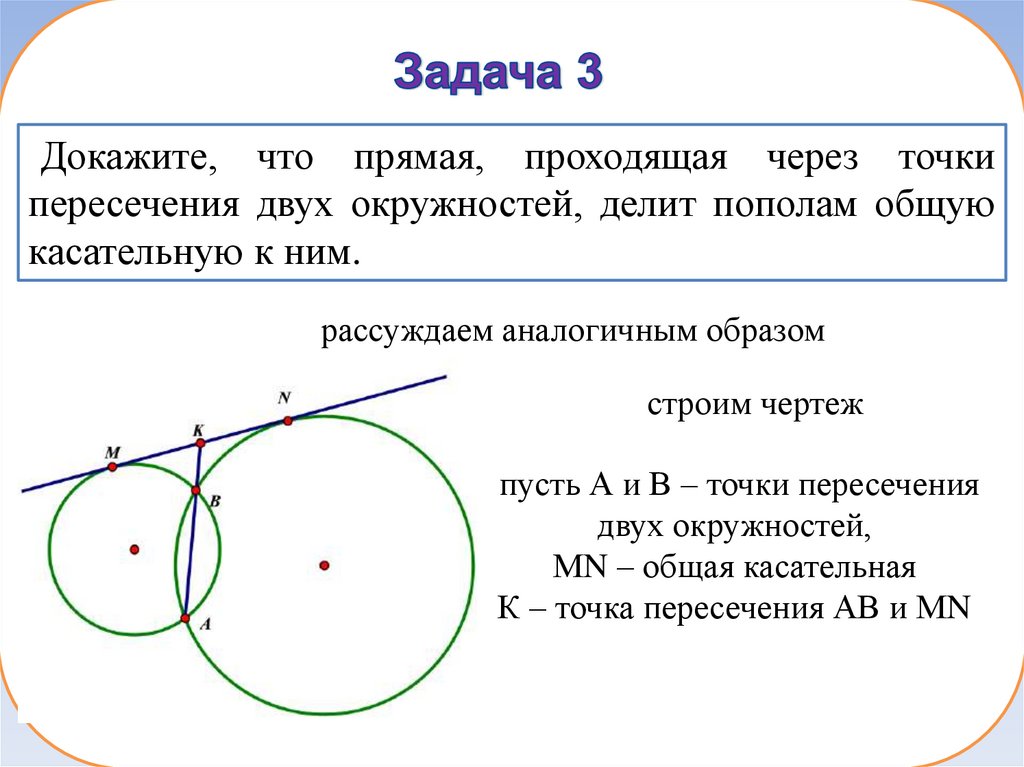
15.

Докажите, что прямая, проходящая через точки
пересечения двух окружностей, делит пополам общую
касательную к ним.
рассуждаем аналогичным образом
строим чертеж
пусть А и В – точки пересечения
двух окружностей,
МN – общая касательная
К – точка пересечения АВ и МN

16.

Докажите, что прямая, проходящая через точки
пересечения двух окружностей, делит пополам общую
касательную к ним.
Доказать: МК = КN
обсуждаем теоретический
материал необходимый
для решения задачи

17.

Докажите, что прямая, проходящая через точки
пересечения двух окружностей, делит пополам общую
касательную к ним.
Что надо знать:
понятие касательной и
секущей
теорему о касательной
и секущей

18.

Докажите, что прямая, проходящая через точки
пересечения двух окружностей, делит пополам общую
касательную к ним.
Из точки К проведены
касательная и секущая КА,
тогда по теореме о
касательной и секущей

19.

Треугольники и их элементы
Теоретический материал необходимый для решения
задач:
признаки равенства треугольников
признаки подобия треугольников
свойства сторон и углов треугольника, площадь
свойства медианы, биссектрисы и высоты треугольника
средняя линия и серединный перпендикуляр
треугольника
равнобедренный, равносторонний и прямоугольный
треугольники
окружность, описанная около треугольника и вписанная
в треугольник

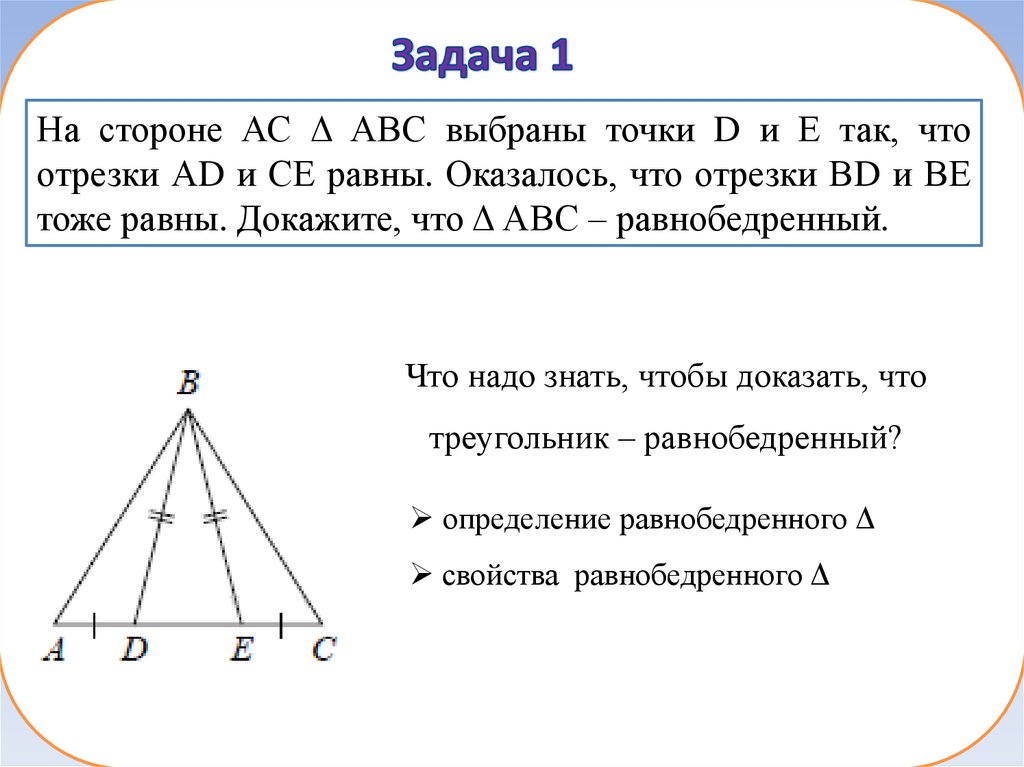
20.

На стороне АС Δ АВС выбраны точки D и Е так, что
отрезки АD и СЕ равны. Оказалось, что отрезки ВD и ВЕ
тоже равны. Докажите, что Δ АВС – равнобедренный.
Что надо знать, чтобы доказать, что
треугольник – равнобедренный?
определение равнобедренного Δ
свойства равнобедренного Δ

21.

На стороне АС Δ АВС выбраны точки D и Е так, что
отрезки АD и СЕ равны. Оказалось, что отрезки ВD и ВЕ
тоже равны. Докажите, что Δ АВС – равнобедренный.
Как доказать равенство углов или сторон?
доказать равенство Δ АВD и Δ ВЕС

22.

Задача для самостоятельного решения
1. Докажите, что если в треугольнике две высоты
равны, то он равнобедренный.

23.

Задача для самостоятельного решения
2. В равностороннем Δ АВС точки М, N, К – середины
сторон АВ, ВС, СА – соответственно. Докажите, что Δ
МNК – равносторонний.

24.

Окружность касается стороны АВ Δ АВС, у которого угол
С = 900 , и продолжений его сторон АС и ВС за точки А и В
соответственно. Докажите, что периметр Δ АВС равен
диаметру этой окружности.
Какой теоретический материал
необходим для решения данной задачи?
понятие периметра и диаметра
окружности
признак и свойства касательной
понятие прямоугольника и
квадрата

25.

Окружность касается стороны АВ Δ АВС, у которого угол
С = 900 , и продолжений его сторон АС и ВС за точки А и В
соответственно. Докажите, что периметр Δ АВС равен
диаметру этой окружности.
по признаку касательной
ОМ АС, ОК ВС , ON АВ
С 900
ОМСК - прямоугольник
ОМ ОК R
ОМСК - квадрат

26.

Окружность касается стороны АВ Δ АВС, у которого угол
С = 900 , и продолжений его сторон АС и ВС за точки А и В
соответственно. Докажите, что периметр Δ АВС равен
диаметру этой окружности.
по свойству отрезков касательных
МА АN , NВ ВК , МС СК
Р АС ВС АВ
АС AN NВ BC
АС AМ ВК BC
МС СК D

27.

Четырехугольники и их элементы
Теоретический материал необходимый для решения
задач:
виды четырехугольников и их свойства
вписанные и описанные четырехугольники
правильные многоугольники

28.

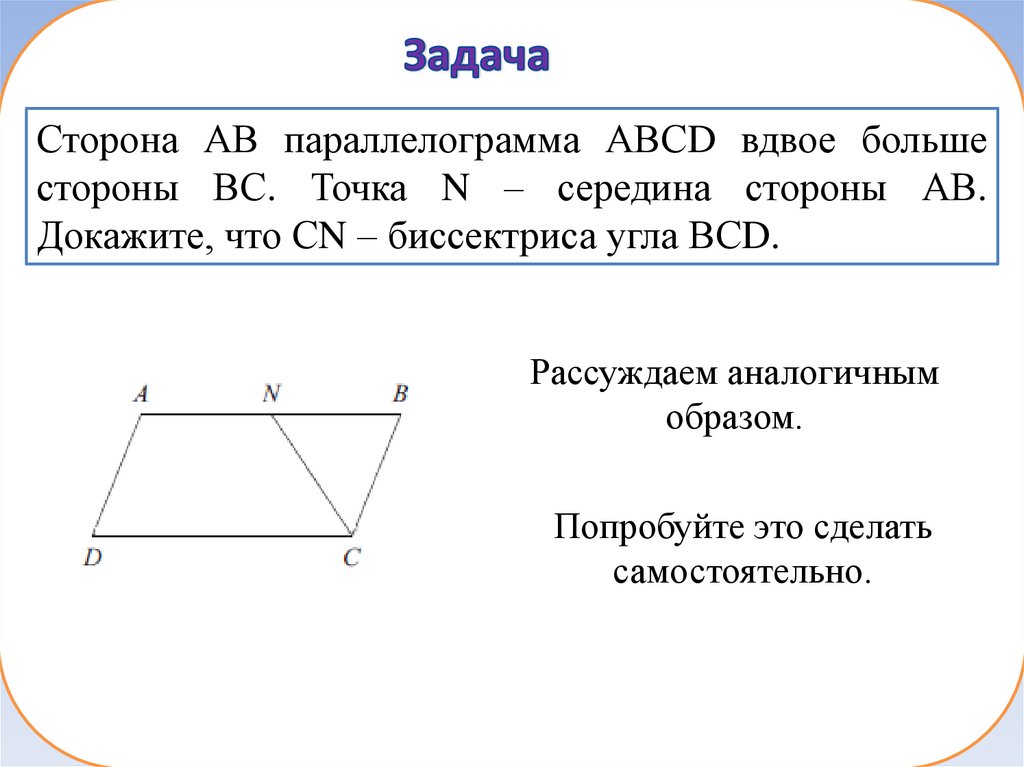
Сторона АВ параллелограмма АВСD вдвое больше
стороны ВС. Точка N – середина стороны АВ.
Докажите, что СN – биссектриса угла ВСD.
Рассуждаем аналогичным
образом.
Попробуйте это сделать
самостоятельно.

29.

Задачи для самостоятельного решения
1. Сторона AB параллелограмма ABCD вдвое больше
стороны AD. Точка K — середина стороны AB. Докажите,
что DK — биссектриса угла ADC.
2. В параллелограмме АВСD точки E, F, K и М лежат на его
сторонах, как показано на рисунке, причём АЕ = CK, BF =
DM. Докажите, что EFKM — параллелограмм.
3. Дана равнобедренная трапеция АВСD. Точка М лежит
на основании АD и равноудалена от концов другого
основания. Докажите, что М — середина основания АD.