Стандартная атмосфера. Лекция 4

1.

стандартная атмосфера
кинематика жидкости
ускорение жидкой частицы
полные производные от
термодинамических параметров
уравнение линии тока
вращательное движение жидкой частицы
деформационное движение жидкой
частицы
деформация скашивания при движении
жидкой частицы
уравнение неразрывности
Фролов В.А. Лекции по аэродинамике, 2020
1

2.

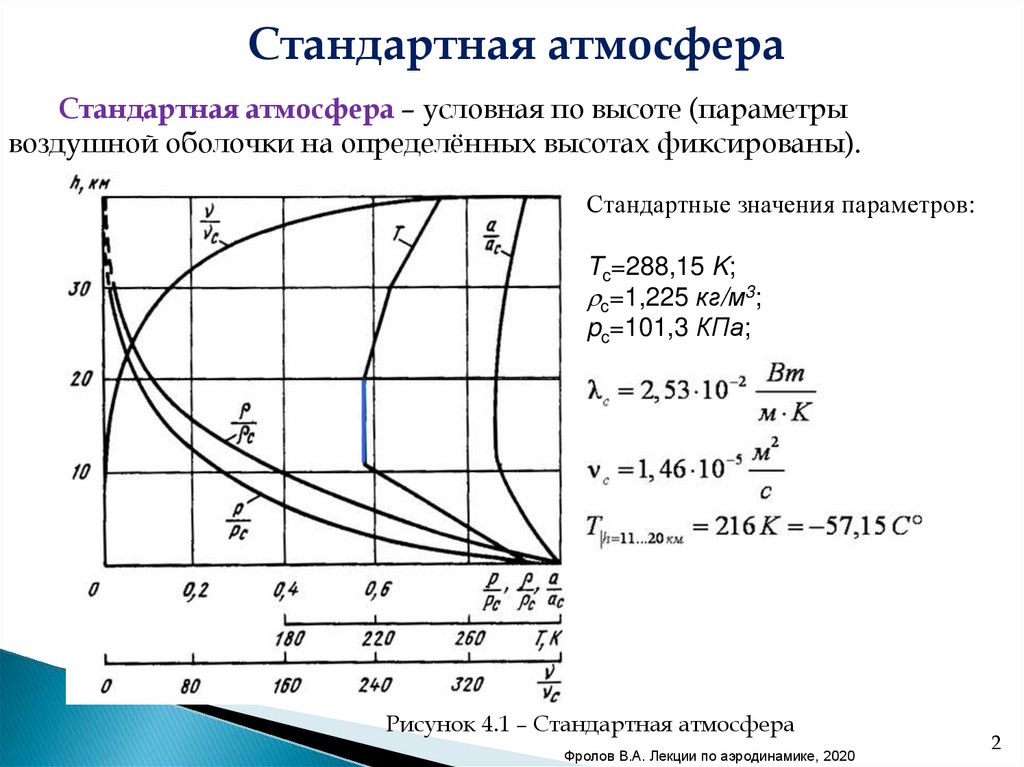
Стандартная атмосфера
Стандартная атмосфера – условная по высоте (параметры
воздушной оболочки на определённых высотах фиксированы).
Стандартные значения параметров:
Tc=288,15 K;
c=1,225 кг/м3;
pc=101,3 КПа;
Рисунок 4.1 – Стандартная атмосфера
Фролов В.А. Лекции по аэродинамике, 2020
2

3.

Кинематика жидкости. Ускорение
Кинематика жидкости – раздел механики, который рассматривает
поле скорости, ускорения и не рассматривает силовое воздействие между
телом и средой.
V V x , y , z , t ; V Vx i V y j V z k
dV V V dx V dy V dz
a
;
dt
t x dt y dt z dt
dx
dy
dz
Vx ,
Vy ,
Vz ;
dt
dt
dt
V
V
V
V
a
Vx
Vy
Vz
;
t
x
y
z
Фролов В.А. Лекции по аэродинамике, 2020
(4.1)
(4.2)
(4.3)
(4.4)
3

4.

Кинематика жидкости. Ускорение
Скалярное произведение двух векторов:
(4.5)
(4.6)
Vx
V
V
V
V
Vy
Vz
V V a
V V
x
y
z
t
(4.7)
(4.8)
- локальное (субстанциональное) ускорение
- конвективное ускорение
Фролов В.А. Лекции по аэродинамике, 2020
4

5.

Кинематика жидкости. Частные производные
(4.9)
(4.10)
(4.11)
(4.12)
d dx dy dz dx dy dz
dt
t x dt y dt z dt t dt x dt y dt z
(4.13)
Vx
Vy
Vz
t
x
y
z
(4.14)
(4.15)
(4.16)
Фролов В.А. Лекции по аэродинамике, 2020
5

6.

Частные производные температуры,
энтальпии и энтропии
(4.17)
Фролов В.А. Лекции по аэродинамике, 2020
6

7.

Линия тока
Рисунок 4.2 – Линия тока
Кривая в пространстве, в каждой точке которой в данный момент
времени вектор скорости совпадает с касательной в этой точке называется
линией тока.
Фролов В.А. Лекции по аэродинамике, 2020
7

8.

Дифференциальное уравнение линии тока
V dr
V dr 0
V Vx ,Vy ,Vz , dr dx, dy, dz
i
j k
Vx Vy Vz
0 i Vy dz Vz dy j Vz dx Vx dz k Vx dy Vy dx 0
dx dy dz
Vy dz Vz dy 0
dx dy dz
V
dx
V
dz
0
z
x
Vx Vy Vz
V dy V dx 0
y
x
dx dy dz
const τ
Vx Vy Vz
Фролов В.А. Лекции по аэродинамике, 2020
8

9.

Уравнение линии тока и траектории
Траектория это след частицы в пространстве.
Если рассматривать установившееся (стационарное) течение, линия
тока и траектория совпадают. Обратное не выполняется.
Дифференциальное уравнение линии тока:
(4.18)
Система дифференциальных уравнений траектории:
dx
dt Vx
dy
Vy
dt
dz
dt Vz
Фролов В.А. Лекции по аэродинамике, 2020
(4.19)
9

10.

Вращательное движение жидкой частицы
Рисунок 4.3 – Общее движение жидкой частицы
Фролов В.А. Лекции по аэродинамике, 2020
10

11.

Вращательное движение жидкой частицы
Будем полагать вектор скорости непрерывной функцией координат и
времени.
Непрерывная функция является дифференцируемой функцией.
Дифференцируемая функцией может быть разложена в ряд Тейлора.
Фролов В.А. Лекции по аэродинамике, 2020
11

12.

Вращательное движение жидкой частицы
Пусть все производные компоненты скорости равны нулю.
Пусть только в момент времени t=const
Vy
x
0
Рисунок 4.4 – Вращательное движение ребра АВ жидкой частицы
Фролов В.А. Лекции по аэродинамике, 2020
12

13.

Вращательное движение жидкой частицы
(4.20)
Vx
0
y
(4.21)
Правило знаков: вращение против часовой стрелки «+», а по часовой – «-»
(4.22)
Фролов В.А. Лекции по аэродинамике, 2020
13

14.

Вращательное движение жидкой частицы
(4.23)
(4.24)
Фролов В.А. Лекции по аэродинамике, 2020
14

15.

Деформационное движение жидкой частицы
Рисунок 4.5 – Деформационное движение ребра АВ жидкой частицы
(4.25)
(4.26)
(4.27)
Фролов В.А. Лекции по аэродинамике, 2020
15

16.

Деформация скашивания при движении
жидкой частицы
(4.28)
Vz Vy
2ezy 2eyz
;
y
z
Vx Vz
2exz 2ezx
.
z
x
Тензор скоростей деформаций
(4.29)
exx exy exz
S eyx eyy eyz
e
e
e
zx zy zz
Фролов В.А. Лекции по аэродинамике, 2020
(4.30)
16

17.

Уравнение неразрывности
Относительное изменение объёма по времени равно
(4.31)
(4.32)
(4.33)
(4.34)
(4.35)
Фролов В.А. Лекции по аэродинамике, 2020
17

18.

Уравнение неразрывности
(4.36)
ρ
div ρ V 0
t
Фролов В.А. Лекции по аэродинамике, 2020
(4.37)
18

19.

Уравнение неразрывности
Частные случаи уравнения неразрывности
1) Установившиеся течение
(4.38)
2) Несжимаемое течение
Vx Vy Vz
ρ const divV 0 divV
x
y
z
Vx Vy Vz
0
x
y
z
(4.39)
divV 0
Фролов В.А. Лекции по аэродинамике, 2020
19