Понятие вероятности случайного события. Лекция №16

1.

Дисциплина: МАТЕМАТИКА
Раздел 5: Теория вероятностей
Лекция №16
Понятие вероятности случайного события
Разработчик: Бредихина Ольга Александровна

2.

5 Теория вероятностей
5.1 Основные понятия
Теория вероятностей – математическая наука, изучающая
закономерности массовых случайных явлений.
Случайное явление – это явление, исход которого
предсказать
невозможно
(при
неоднократном
воспроизведении одного и того же опыта оно протекает
каждый раз несколько по-иному).
Цель теории вероятностей: осуществление прогноза в
области случайных явлений, влияние на ход этих явлений,
их контроль, ограничение сферы действия случайности.

3.

5 Теория вероятностей
5.1 Основные понятия
Пусть производится опыт: бросание игральной кости.
Пусть даны события:
А – выпадение пяти очков;
B – выпадение чётного числа очков;
С – выпадение семи очков;
D – выпадение целого числа очков;
Е – выпадение не менее трёх очков
Ω={ω1, ω2, ω3, ω4, ω5, ω6}, где элементарные
равновозможные события ωi означают, что в результате
бросания кости выпало i очков, где i=1, 2, 3, 4, 5, 6.
События ωi образуют полную группу событий.
D – достоверное событие, C – невозможное событие, A,
B, E – случайные события.
A и B – несовместные события, A и E – совместные
события

4.

5 Теория вероятностей
5.1 Основные понятия
Для количественной оценки возможности появления
случайного события А вводится понятие вероятности.
Вероятностью события называется численная мера
степени объективной возможности наступления события.
Основные виды вероятности:
статистическая вероятность;
классическая вероятность;
геометрическая вероятность

5.

5 Теория вероятностей
5.2 Статистическое определение вероятности
Пусть производится n одинаковых опытов и пусть в m из
них событие А произошло.
m
Назовём отношение W A
n
относительной частотой появления события А.
Если при увеличении числа опытов относительная частота
события колеблется около некоторого фиксированного
числа, то говорят, что событие А устойчиво, и это число
называют статистической вероятностью события А.

6.

5 Теория вероятностей
5.2 Статистическое определение вероятности
Статистическая
вероятность
в
отличие
от
«математической» вероятности является характеристикой
опытной, экспериментальной.
Пример 1 Статистическая вероятность попадания в цель
при 75 выстрелах равна 0,6. Сколько было попаданий?
Решение.
По условию n=75, W(A)=0,6.
Тогда искомое количество попаданий в цель, то есть
количество испытаний, в которых событие А (попадание в
цель) произошло, вычисляется по формуле: m=n·W(A),
откуда находим m=75·0,6=45 попаданий.
Ответ: 45.

7.

5 Теория вероятностей
5.2 Статистическое определение вероятности
Пример 2 Для пошива школьных форм было заказано
2200 пуговиц. При проверке партии из 500 пуговиц было
обнаружено 6 бракованных. Какое наименьшее количество
запасных пуговиц необходимо еще заказать, чтобы
исключить брак?
Решение.
Статистическая частота брака будет составлять
6
W ( A)
0,012 , тогда среди 2200 пуговиц число
500
бракованных m=2200·0,012=26,4.
Округлив это число до наибольшего ближайшего целого,
получим 27 пуговиц.
Ответ: 27.

8.

5 Теория вероятностей
5.3 Классическое определение вероятности
Недостаток статистической вероятности – она
определяется
только
после
проведения
опыта.
Классическое определение вероятности лишено этого
недостатка.
Вероятностью события А называется отношение числа
благоприятствующих этому событию исходов к общему
числу всех равновозможных несовместных элементарных
исходов, образующих полную группу:
Наряду с обозначением Р(А) для вероятности события А
используется обозначение р, то есть р=Р(А).

9.

5 Теория вероятностей
5.3 Классическое определение вероятности
Понятие вероятности является одним из основных в
теории вероятностей. Данное выше определение является
классическим. Из него вытекают некоторые свойства:
Свойство 1. Вероятность достоверного события равна
единице, то есть Р(Ω)=1.
Свойство 2. Вероятность невозможного события равна
нулю, то есть Р(∅)=0.
Свойство 3. Вероятность случайного события есть
положительное число 0<P(A)<1.

10.

5 Теория вероятностей
5.3 Классическое определение вероятности
При решении задач по классической вероятности можно
воспользоваться следующими способами:
использование определения;
перебор;
использование таблицы.

11.

5 Теория вероятностей
5.3 Классическое определение вероятности
Решение задач с использованием определения
Пример 3 Фабрика выпускает насосы. В среднем на 89
качественных насосов приходится 11, имеющих скрытые
дефекты. Найти вероятность того, что выбранный в
магазине насос окажется с дефектом.
Решение.
P A
11
11
0,11
89 11 100
Пример 4 Игральная кость бросается один раз. Какова
вероятность того, что число очков, выпавших на верхней
грани, будет не меньше четырёх?
Решение.
P A
3
0,5
6

12.

П
5 Теория вероятностей
5.3 Классическое определение вероятности
Решение задач с использованием определения
Пример 5 Конференция длится 4 дня. Запланировано 80
докладов: первые два дня по 23 доклада, остальные
распределены поровну между третьим и четвёртым днями.
Порядок докладов определяется жеребьёвкой. Какова
вероятность того, что доклад профессора А окажется
запланированным на третий день конференции?
Решение.
1 день: 23 доклада;
2 день: 23 доклада;
3 день: 17 докладов;
4 день 17 докладов.
Ответ: 0,2185.
P A
17
0,2125
80

13.

5 Теория вероятностей
5.3 Классическое определение вероятности
Решение задач с использованием перебора
Пример 6 Найти вероятность
того, что при трёх бросаниях
монеты «орёл» выпадет ровно
один раз.
Решение.
ООО
ООР
ОРО
РОО
3
P A 0,375
ОРР
8
РОР
РРО
РРР
Пример 7 Какова вероятность
получить слово КОЛ из букв О,
Л, К?
Решение.
ОЛК
ЛОК
ЛКО
КЛО
КОЛ
ОКЛ
P A
1
6

14.

5 Теория вероятностей
5.3 Классическое определение вероятности
Решение задач с использованием таблицы
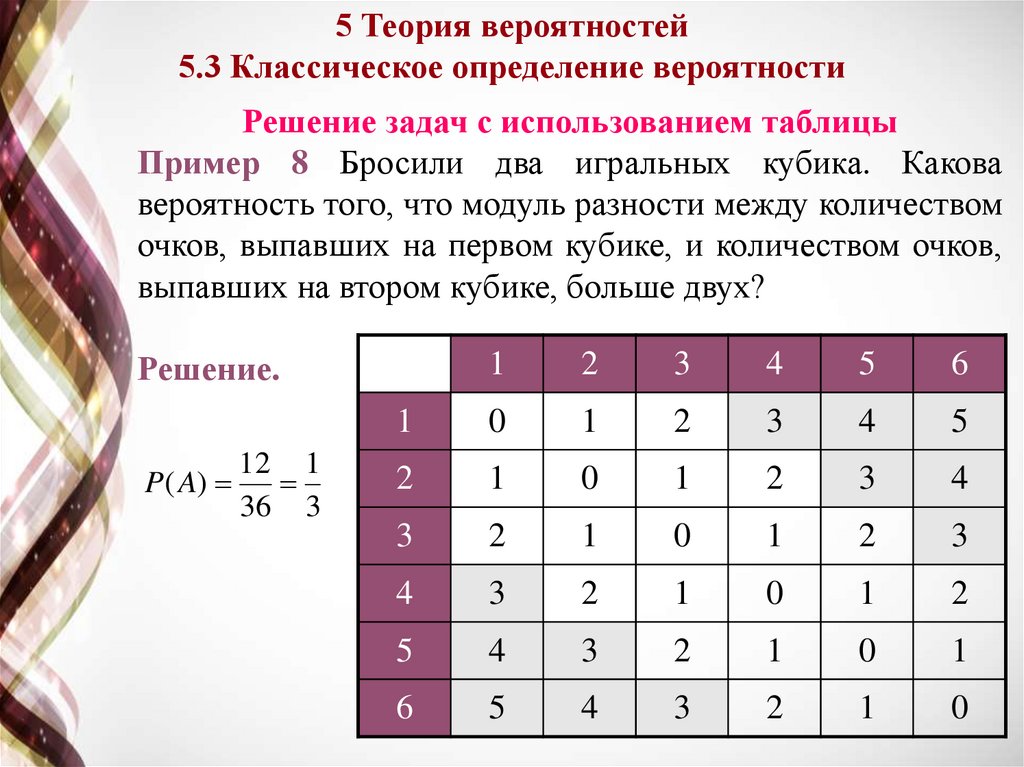
Пример 8 Бросили два игральных кубика. Какова
вероятность того, что модуль разности между количеством
очков, выпавших на первом кубике, и количеством очков,
выпавших на втором кубике, больше двух?
Решение.
P ( A)
12 1
36 3
1
2
3
4
5
6
1
0
1
2
3
4
5
2
1
0
1
2
3
4
3
2
1
0
1
2
3
4
3
2
1
0
1
2
5
4
3
2
1
0
1
6
5
4
3
2
1
0

15.

5 Теория вероятностей
5.4 Геометрическое определение вероятности
Классическое определение вероятности нельзя применять
к испытаниям с бесконечным числом исходов. Для
описания такой ситуации вводят понятие геометрической
вероятности, то есть вероятности попадания точки в
область.
Геометрическая вероятность события А – это
отношение меры области g, благоприятствующей
появлению события А, к мере всей области G возможных
исходов события А:
mes g
P( A)
mes G
mes – мера (длина, площадь, объём).

16.

5 Теория вероятностей
5.4 Геометрическое определение вероятности
Недостатки геометрической вероятности: в случае
классического определения вероятность достоверного
события равна единице Р(Ω)=1, а вероятность
невозможного события равна нулю Р(∅)=0. Справедливо и
обратное утверждение. В случае геометрической
вероятности обратное утверждение не верно!
Пример 9 Дан квадрат, в нём линия, длиной L. Найти
вероятность попадания точки М на линию.
Решение.
P( A)
S
mes g
L 0
линии 2 0
mes G S квадрата a
Вероятность получилась равной нулю,
хотя это событие может произойти.
M
a
L
a

17.

5 Теория вероятностей
5.4 Геометрическое определение вероятности
Пример 10 Обедая за столом шириной 2 м, вы увидели
ползущего с другого конца стола на ваш край таракана.
Какова вероятность того, что, доползя до края стола,
таракан проползет справа от вас, если вы сидите по центру
стола и занимаете вдоль него 60 см, а таракан очень
худой?
Решение. Выражение «таракан очень худой» означает, что
таракан может восприниматься материальной точкой, то
есть он не занимает места на столе. Поэтому искомая
вероятность считается по формуле геометрической
вероятности:
60
l 200 60
7
P( A)
: 200
0,35
L
2
20
200

18.

5 Теория вероятностей
5.4 Геометрическое определение вероятности
Пример 11 Стержень длиной L разламывают на две части
в случайной точке. Найти вероятность того, что меньший
отрезок имеет длину не более, чем L 5 .
Решение.
L/ 5
L/ 5
L
L L
l 5 5 2
P ( A)
L
L
5

19.

5 Теория вероятностей
5.4 Геометрическое определение вероятности
Пример 12 Внутрь правильного треугольника наудачу
брошена точка. Найти вероятность того, что точка
окажется внутри вписанного в треугольник круга.
Решение.
P A
SO
S ABC
r2
S ABC
2 S ABC 2 S ABC
, где r
a a a
3a
2
2 S ABC
4 S ABC
3a
P A
2
S ABC
9
a
B
1
1
3 2
S ABC a 2 sin A a 2 sin 600
a
2
2
4
4
P A
9
3 2 2
3
a : a
0,6
9
4
a
O
a
r
A
H
a
C

20.

5 Теория вероятностей
5.4 Геометрическое определение вероятности
Пример 13 На плоскости начерчен квадрат, ограниченный
осями координат и прямыми х=1 и y=1. Найти вероятность
того, что точка, брошенная наудачу в этот квадрат, попадёт
в область
Решение.
P A
y
S заштрихованной области
y= x
S квадрата
1
1
S заштрихованной области 1 x dx
0
1
1,5
0
1
x
2 1
x
1
0 1,5 0
3 3
Sквадрата 1 1 1
1
1
P A : 1
3
3
1
x

21.

5 Теория вероятностей
Наряду
со
статистическим,
классическим
и
геометрическим
определениями
вероятности,
в
приложениях иногда рассматривают субъективную
вероятность, получаемую как степень уверенности в
наступлении того или иного события на основании
обработки мнений экспертов.
Субъективная вероятность может быть использована,
например, при прогнозировании доходности активов,
прибыли от инвестиций и т.п.