Похожие презентации:
Электро-магнитные волны. Лекция 7
1.
Г. Герц о своём открытии электромагнитных волн :“Это абсолютно бесполезно. Это только
эксперимент, который доказывает, что маэстро
Максвелл был прав” – (1888 г.)
2.
Лекция 7. Электромагнитные волны3.
2.1. Два уравнения Максвелла (две гипотезы)2.1.1. Первая гипотеза Максвелла: “Вихревое электрическое поле”
Что «толкает электроны»
?
i
*
E dl
"C "
*
ЭМИ “по Максвеллу” :
C E dl t B dS (I)
B
E
2.1.2. Вторая гипотеза Максвелла: “Ток смещения”
t
E
I см εε0
dS
t
Теорема о циркуляции
“по Максвеллу” :
E
B dl 0 j dS 0 t dS
C
E
t
(II)
B
4.
1) Среда однородная и непроводящая. Следовательно, в нейне может быть токов проводимости;
j dS 0
2) Е и В зависят только от одной пространственной
координаты, например, х – т.е.
Е Е ( x, t )
и
B B ( x, t )
(волна плоская)
;
5.
2.2. Вывод волнового уравнения(ЭМИ “по Максвеллу”)
E
d
l
B
d
s
;
(
I
)
t
"
C
"
" 1 "
1
Теорема о циркуляции
B dl
E
d
s
(
II
)
“по Максвеллу” :
0
0
"C "
t " "
2
2
E E ( x, t )
" плоская волна"
B B ( x, t )
6.
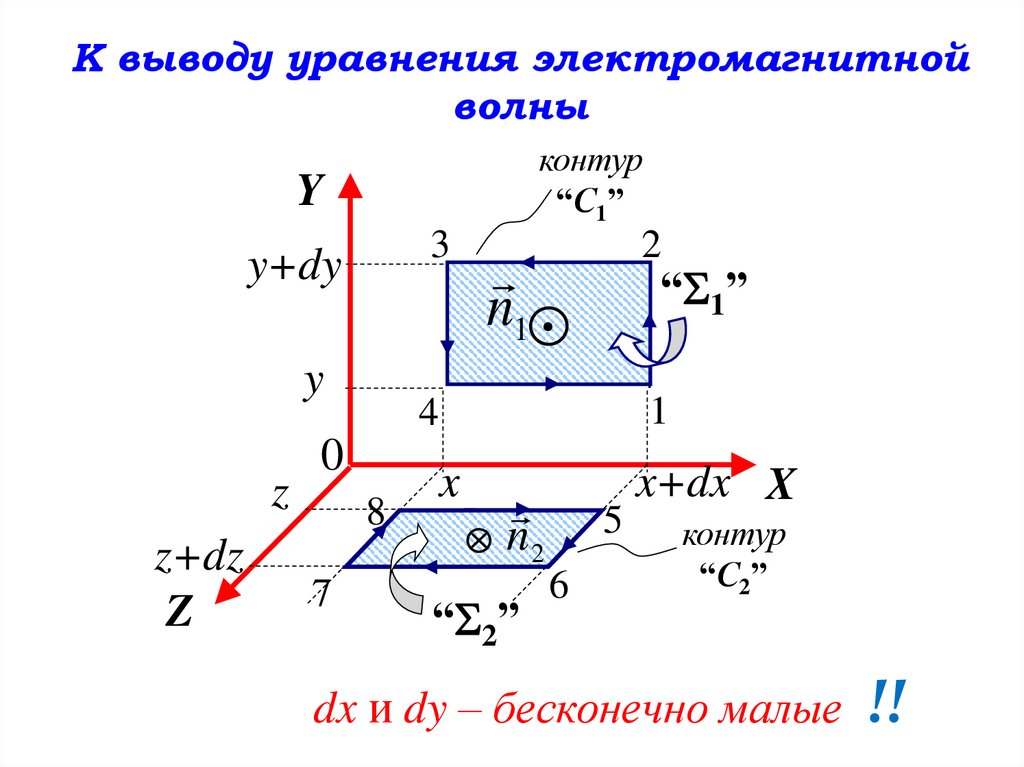
К выводу уравнения электромагнитнойволны
контур
“С1”
Y
3
y+dy
y
z
z+dz
Z
n1
“ 1”
1
4
0
8
7
2
x
n2
“ 2”
5
6
x+dx X
контур
“С2”
dx и dy – бесконечно малые
!!
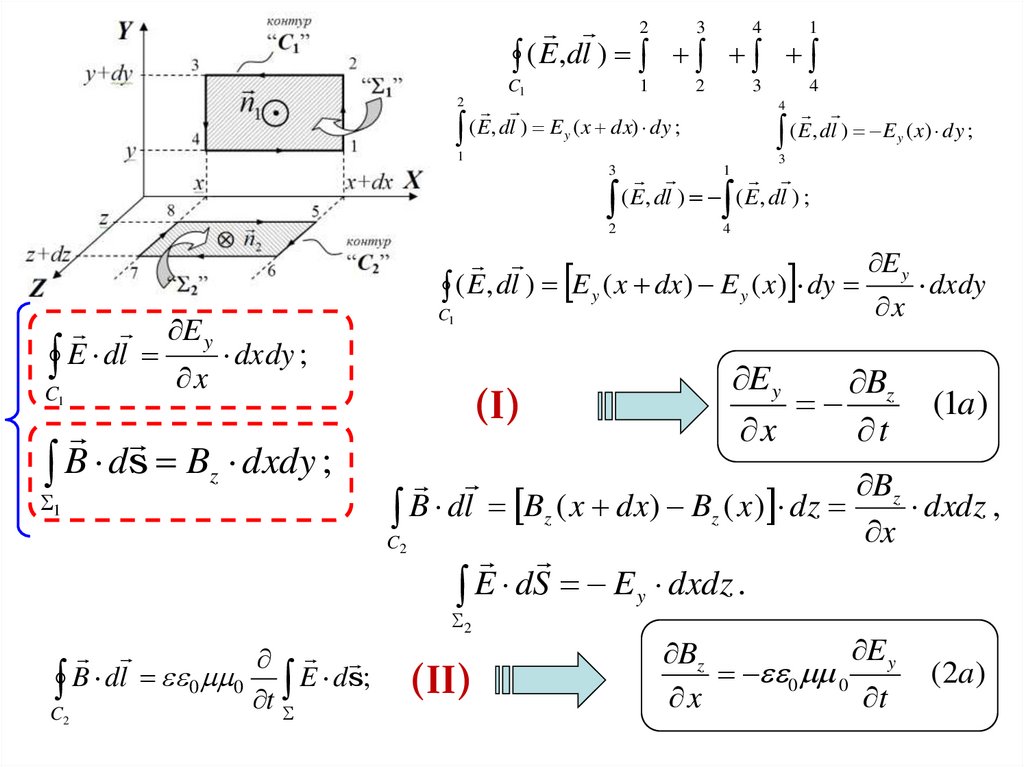
7.
34
1
2
( E ,dl )
2
C1
1
2
3
( E, dl ) E y ( x dx) dy ;
1
3
2
E y
E dl x dxdy ;
C
1
(I)
2
3
( E, dl ) ( E, dl ) ;
1
4
E y
x
Bz
t
(1a )
Bz
B
d
l
B
(
x
dx
)
B
(
x
)
dz
dxdz ,
z
z
x
C2
E dS E y dxdz .
2
B dl 0 0 t E ds;
C
( E , dl ) E y ( x) dy ;
E y
(
E
,
d
l
)
E
(
x
dx
)
E
(
x
)
dy
dxdy
y
y
x
C1
1
B ds Bz dxdy ;
4
4
(II)
E y
Bz
0 0
x
t
(2a )
8.
(...)… а теперь дифференцируем эти равенства по координате:
x
и, меняя последовательность дифференцирования в правой части,
делаем подстановки
2 Bz
E y
0 0
2
t x
x
2Ey
Bz
2
x
t x
2 Ey
x
2
0 0
2 Ey
2 Bz
2 Bz
0 0
2
x
t 2
t 2
Или :
2Ey
t
2
v
2
Ey
2
x
v
2
2
2 Bz
Bz
2
v
2
2
t
x
,
1
0 0
9.
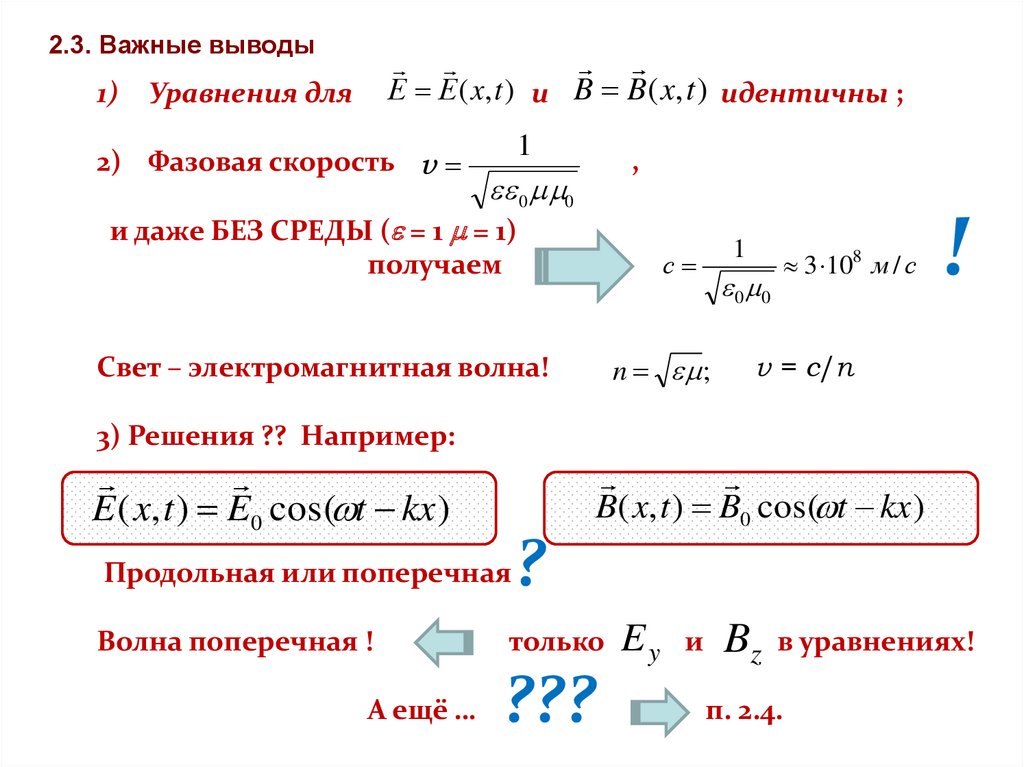
2.3. Важные выводы1)
Е Е ( x, t ) и B B( x, t ) идентичны ;
Уравнения для
2) Фазовая скорость v
1
,
0 0
и даже БЕЗ СРЕДЫ ( = 1 = 1)
получаем
1
с
0 0
n ;
Свет – электромагнитная волна!
3 108 м / с
!
v = c/п
3) Решения ?? Например:
E ( x, t ) E0 cos( t kx )
B( x, t ) B0 cos( t kx )
Продольная или поперечная
Волна поперечная !
А ещё …
?
только
???
Ey
и
Bz
в уравнениях!
п. 2.4.
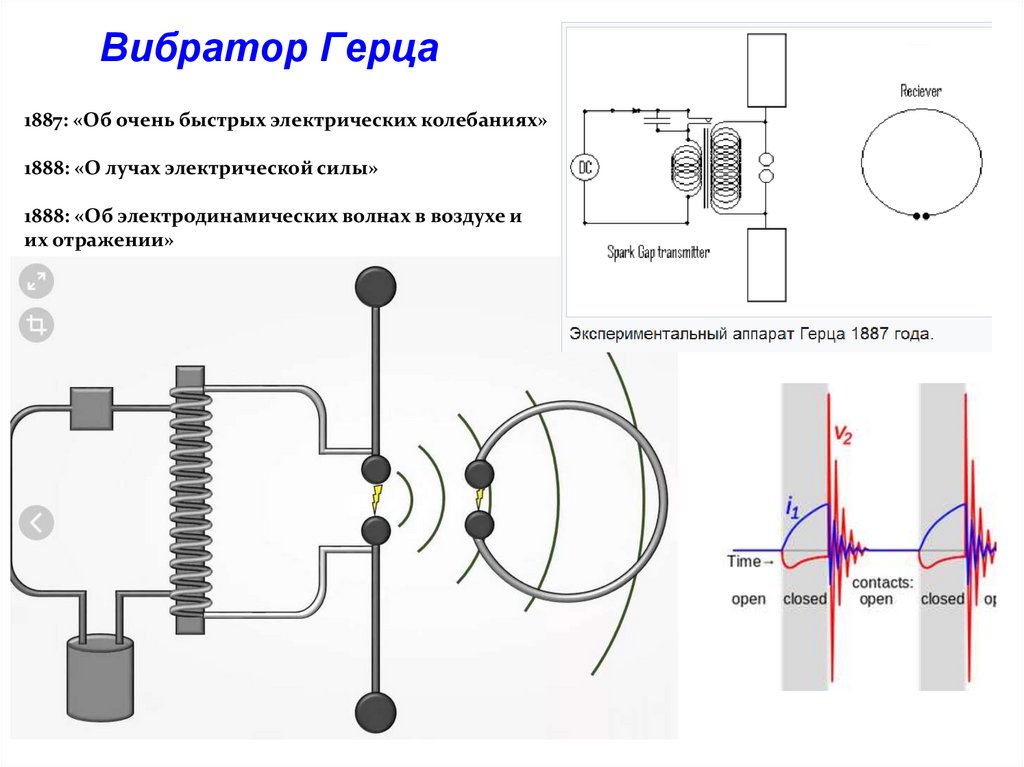
10. Вибратор Герца
1887: «Об очень быстрых электрических колебаниях»1888: «О лучах электрической силы»
1888: «Об электродинамических волнах в воздухе и
их отражении»
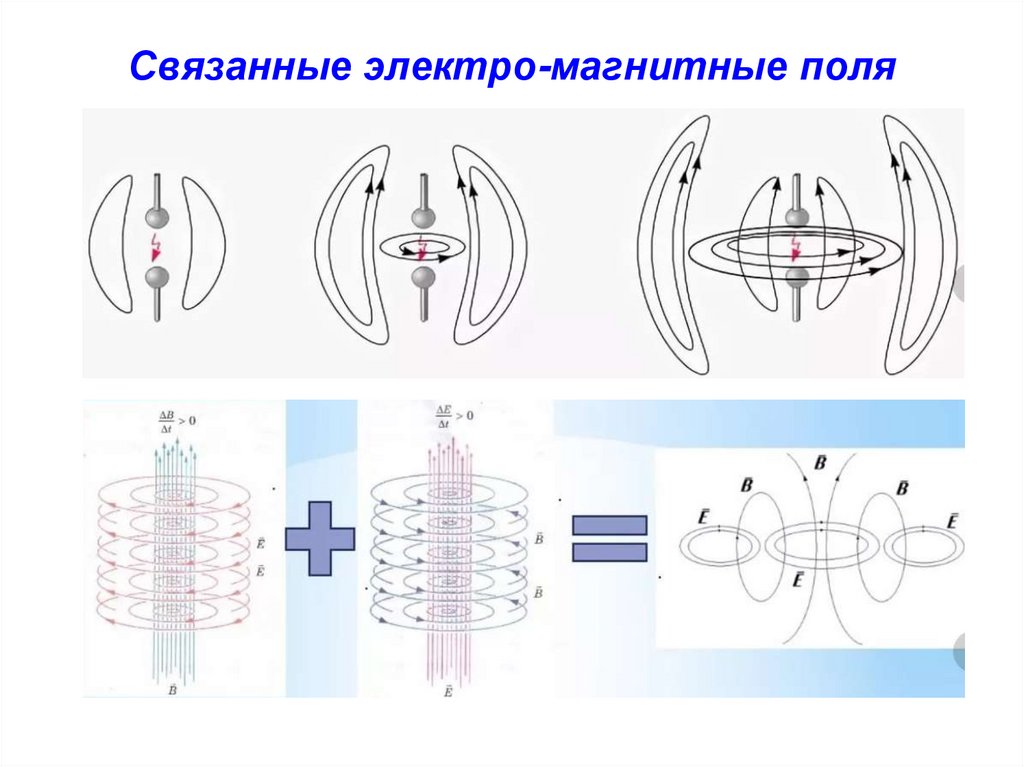
11. Связанные электро-магнитные поля
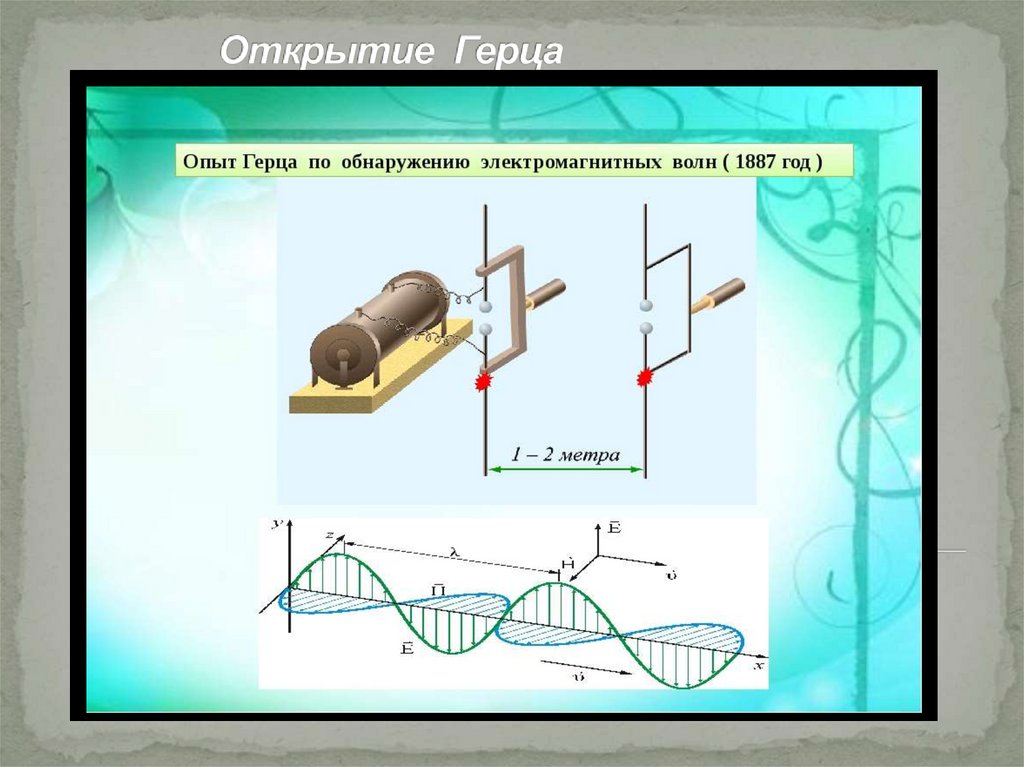
12. Открытие Герца
13. Открытие Герца
1888: “Это абсолютно бесполезно. Это толькоэксперимент, который доказывает, что маэстро
Максвелл был прав” – Г. Герц
14. Приёмник Попова 1895
15.
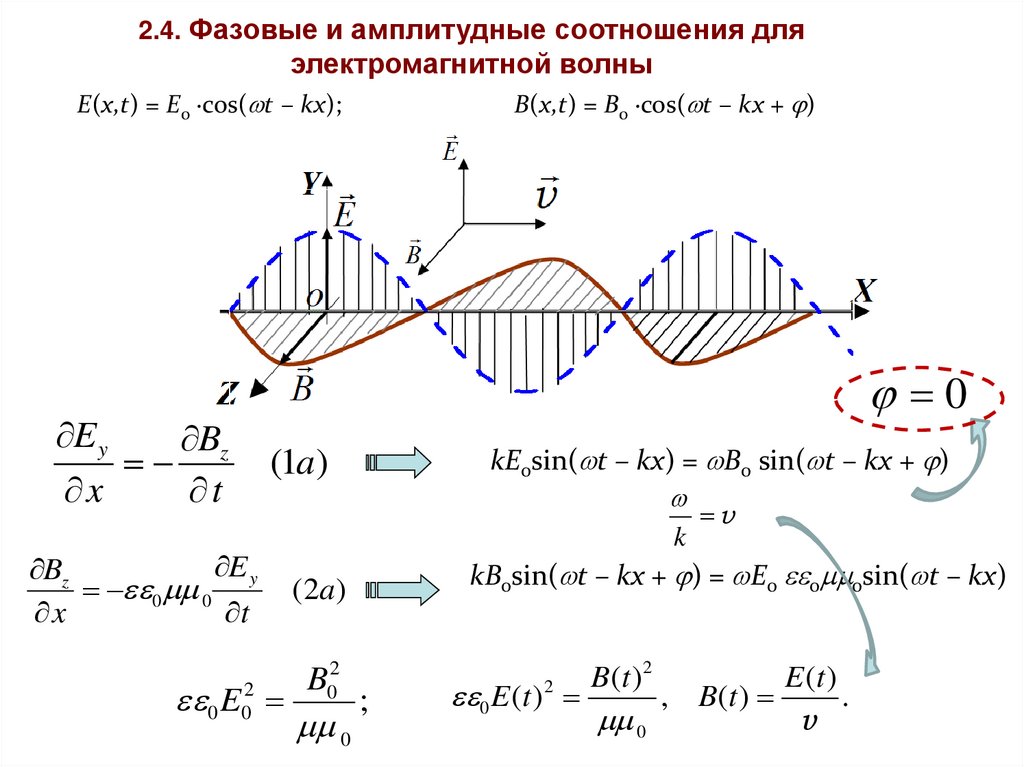
2.4. Фазовые и амплитудные соотношения дляэлектромагнитной волны
E(x,t) = E0 ∙cos( t – kx);
B(x,t) = B0 ∙cos( t – kx + )
0
E y
Bz
x
t
kE0sin( t – kx) = B0 sin( t – kx + )
v
k
kB0sin( t – kx + ) = E0 0 0sin( t – kx)
(1a )
E y
Bz
0 0
x
t
0 E
2
0
(2a )
B02
0
;
0 E (t )
2
B (t ) 2
0
, B (t )
E (t )
.
v
16.
2.5. Характеристики переноса энергии электромагнитной волнойwE
0 E
2
0 E
2
2
wB
B2
0
B2
2 0
B2
EB
w wE wB 0 E
0 0v
2
Плотность потока энергии
S (t ) w(t ) v =
S (t ) w(t ) v
0
Вектор
[ E , B]
0
Φ S ds S n ds
Интенсивность
E (t ) B(t )
E0 B0
I S (t ) w(t ) v
2 0
Пойнтинга
Поток
[E , B ]
S (t ) w(t ) v 0 0
2 0
Φ
S (t ) ds Sn (t ) ds
(Пример: задача 7.23)
17.
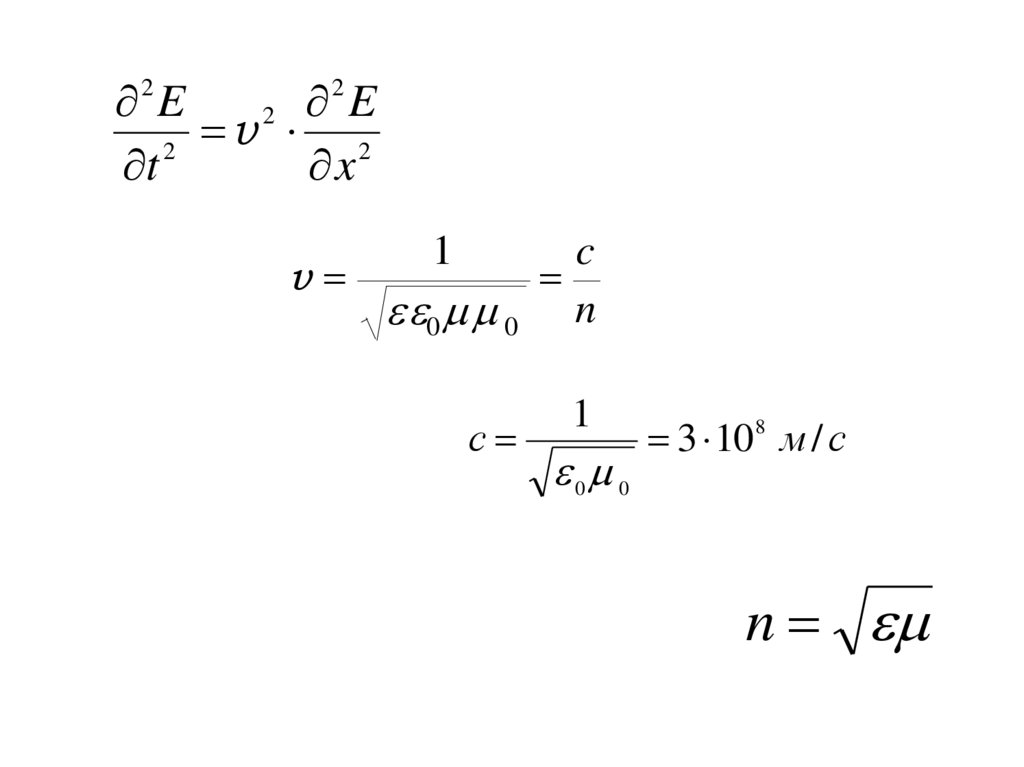
E2 E
v 2
2
t
x
2
2
v
1
0 0
с
c
n
1
0 0
3 10 8 м / с
n
18.
нмнм
, нм









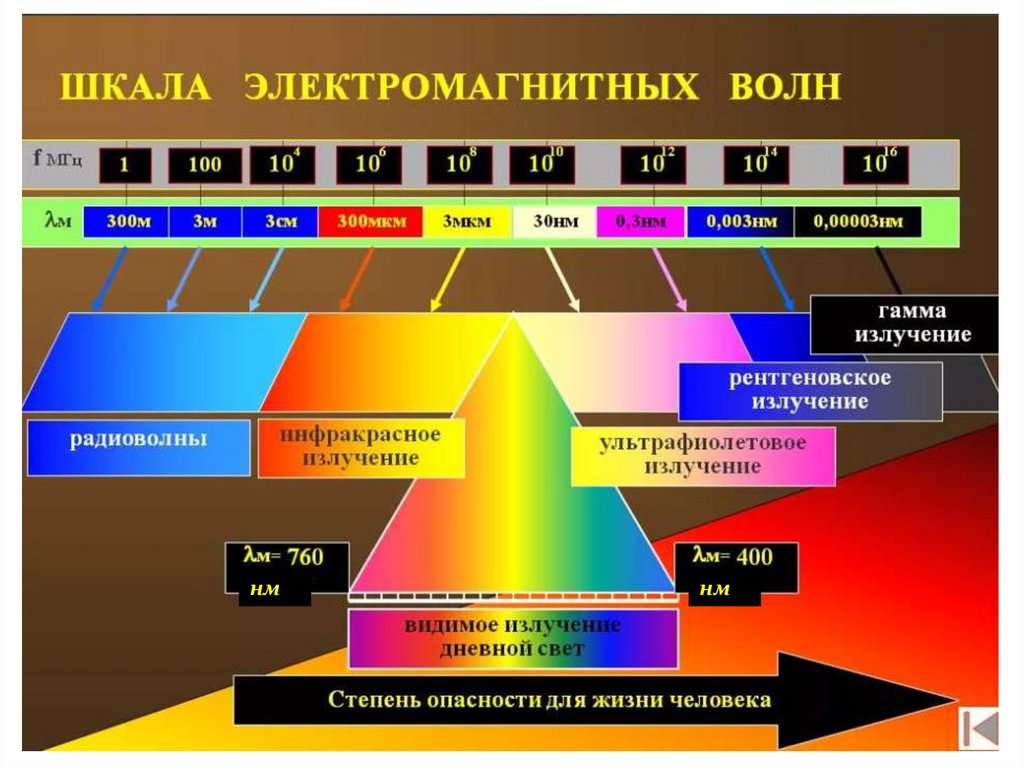
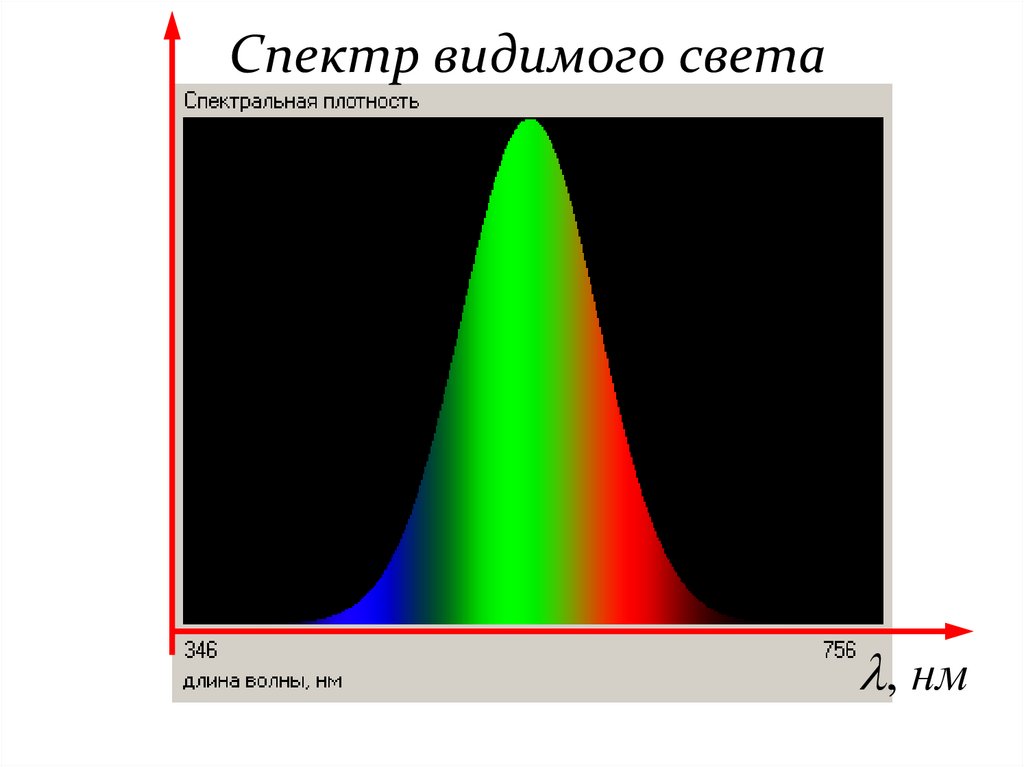
 Физика
Физика








