Похожие презентации:
Электромагнитные волны. Лекция 11
1.
Лекция 11. Электромагнитные волны1.Волновое уравнение для электромагнитного
поля, его общее решение.
2.Скорость распространения электромагнитных
волн.
3.Энергия и импульс электромагнитного поля.
4.Вектор Пойнтинга.
5.Теорема Пойнтинга.
2.
Мы знаем действия многих причин, ноне знаем причин многих действий.
К. Колтон
Мысли философов – как звезды, они
не дают света, потому что слишком
возвышенны.
Ф. Бэкон
А.С. Чуев, 2020
3.
Уравнение волныУравнение волны – математическое выражение,
описывающее смещение колеблющейся частицы в
виде функции, зависящей от координат и времени.
( x, y , z , t )
Для одномерного случая возможное общее решение:
x
x ct
( x, t ) f ( x ct ) F (t ) F (
)
c
c
А.С. Чуев, 2020
4.
Гармоническая волна:А.С. Чуев, 2020
5.
Уравнение плоской гармонической волны:ξ a cos(ωt k r )
Уравнение плоской одномерной гармонической волны:
ξ a cos(ωt kx)
Уравнение плоской одномерной затухающей
гармонической волны:
ξ a0 e
x
cos(ωt kx)
Уравнение сферической гармонической волны:
a0
ξ cos(ωt kr)
r А.С. Чуев, 2020
6.
2 t ωξ Acos
r
v
T
t r
A cos 2
T
k
ω 2
k
- волновое число
v
λ
ω 2
k n n
v
λ
- волновой вектор
В направлении распространения волны
t r
T
- Фазовая скорость
Если общее выражение
дважды продифференцировать по
времени и координатам, то получим
волновое уравнение второго порядка
А.С. Чуев, 2020
7.
Уравнение плоской волныПлоская волна при х = 0
Амплитуда волны на расстоянии l :
где:
Можем записать
А.С. Чуев, 2020
8.
Обозначая- волновой вектор.
2π
k
λ
- волновое число.
Получим
Тут
Общее выражение для уравнения волны
Далее - вывод волнового уравнения из уравнения волны
А.С. Чуев, 2020
9.
Продифференцируем функцию дважды по каждой переменнойА.С. Чуев, 2020
10.
А.С. Чуев, 202011.
Для одномерной плоской волны волновое уравнение имеетвид:
Запомнить:
2π
k
λ
А.С. Чуев, 2020
12.
А.С. Чуев, 202013.
Вибратор ГерцаR – разрядник;
Т - газоразрядная трубка;
D – дроссели.
Вибратор
Резонатор
Движущийся с ускорением электрический
испускает электромагнитные волны.
А.С. Чуев, 2020
заряд
14.
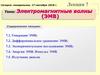
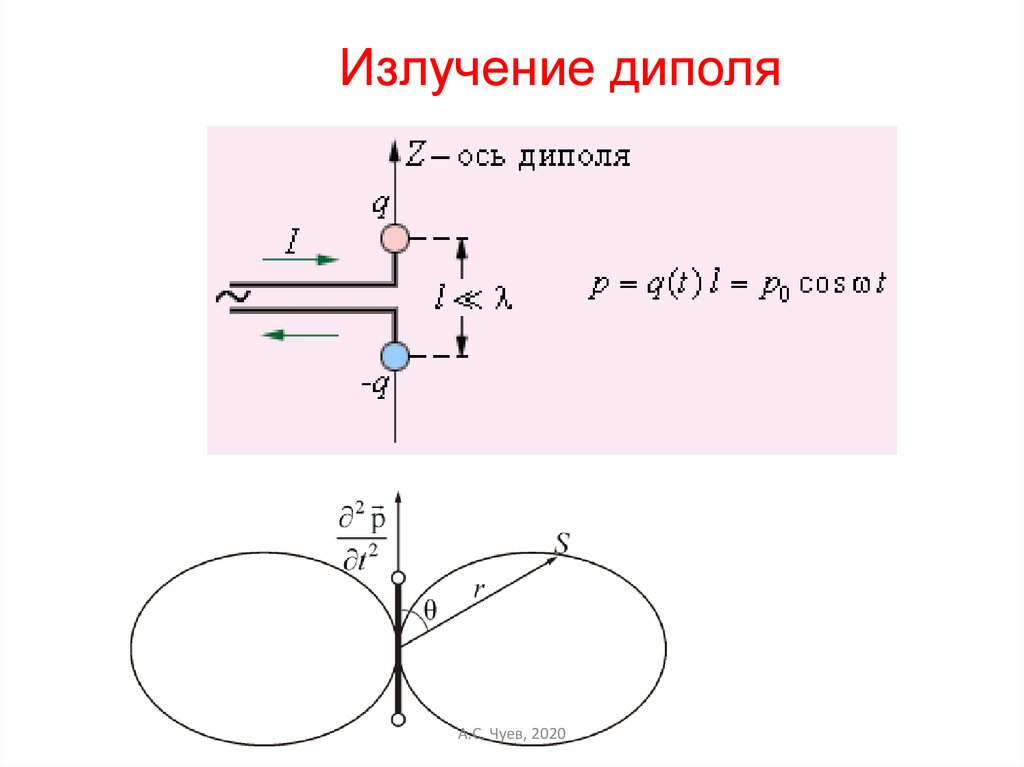
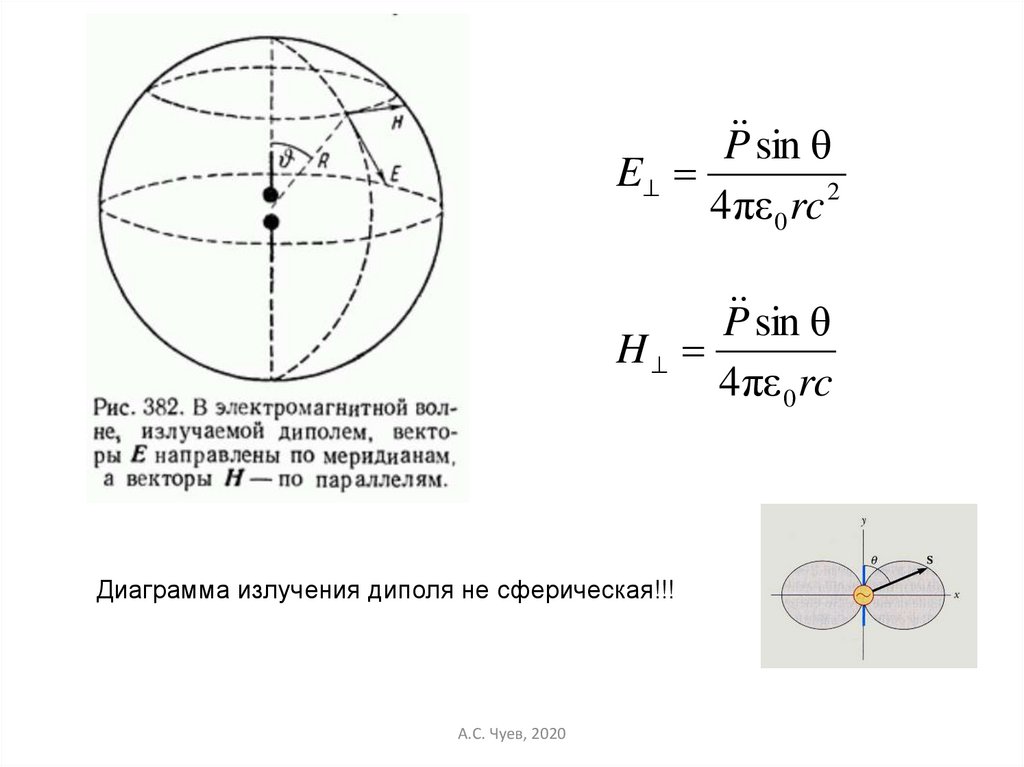
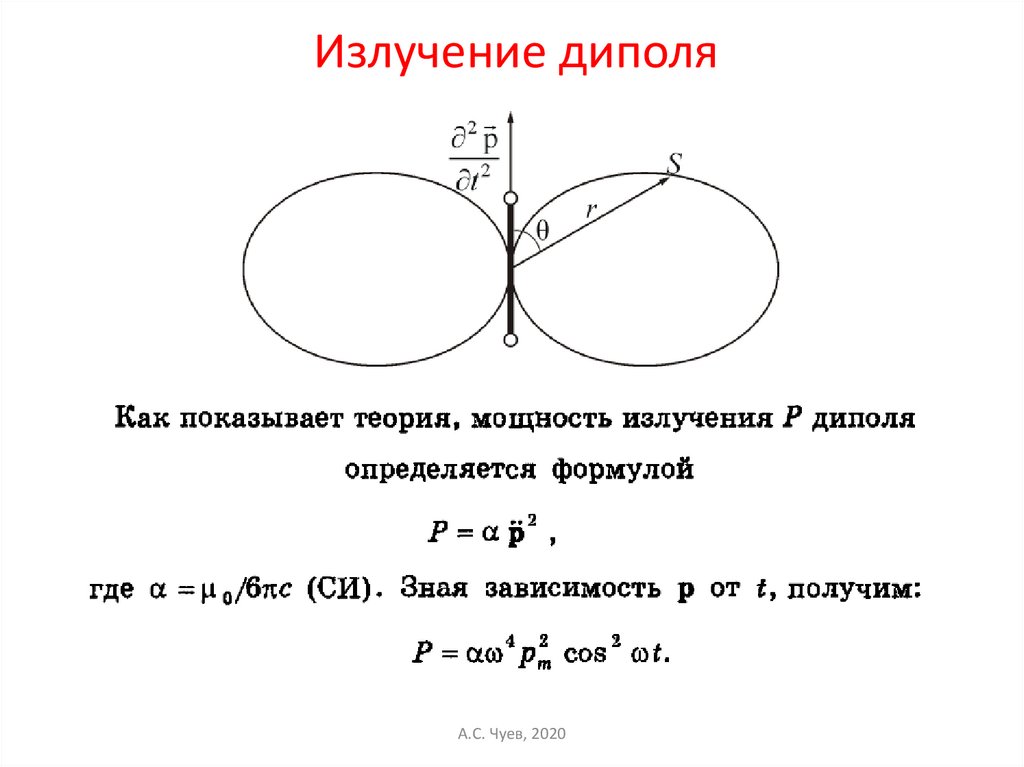
Излучение диполяА.С. Чуев, 2020
15.
А.С. Чуев, 202016.
А.С. Чуев, 202017.
sin θP
E
4πε 0 rc 2
sin θ
P
H
4πε 0 rc
Диаграмма излучения диполя не сферическая!!!
А.С. Чуев, 2020
18.
ФАРА.С. Чуев, 2020
19.
А.С. Чуев, 202020.
А.С. Чуев, 202021.
Электромагнитная волнаУравнения Максвелла при отсутствии источников поля
первого уравнения
А.С. Чуев, 2020
22.
Вывод волнового уравнения из уравнений МаксвеллаПреобразуя векторное произведение в
правой части последнего уравнения:
И использовав для rot Н, выражение из ур-ий Максвелла
получим:
В левой части:
В итоге:
С учетом
А.С. Чуев, 2020
23.
Аналогичным путем можно получитьА.С. Чуев, 2020
24.
Второй вариант вывода волнового уравненияE y
H z
μμ0
x
t
дифференцируем по х
E y
H z
εε0
x
t
дифференцируем по t
Исключая из полученных уравнений смешанную производную, получаем:
2 Ey
x
2
εε0μμ0
2 Ey
t 2
Используя соотношение
2 Ey
x 2
2
εμ E y
2
c t 2
1
ε 0μ 0 2
c
получим
Аналогично можно получить волновое
уравнение и для вектора Н.
А.С. Чуев, 2020
25.
Другой вид волновых формул для электромагнитных волн1 d E
2
E 2 2
υ dt
2
1 d H
2
H 2 2
υ dt
2
2
где
2
2
d
d
d
2 2 2
dx dy
dz
2
υ – фазовая скорость.
А.С. Чуев, 2020
– оператор Лапласа,
26.
Еще один вариант записи волновых уравнений дляэлектромагнитных волн
А.С. Чуев, 2020
27.
Уравнения Максвелла можно решить подстановкой:A
E grad
t
где
и
A
обязаны удовлетворять уравнениям:
1 A
2
A 2 2 0 j
c t
1
2 2
c t
0
2
2
2
Там, где
Верно общее
уравнение:
и
B rotA
j
равны нулю (в вакууме)
2
1
2
2 2 0
c t
В и Н тоже удовлетворяют этому общему уравнению.
А.С. Чуев, 2020
28.
Соотношение Е и В в плоской электромагнитной волнеE Emax cos kx t
B Bmax cos kx t
E
kEmax sin kx t
x
B
Bmax sin kx t
t
E
B
x
t
Из условия синфазности
векторов Е и В в волне
kEmax Bmax
Emax
c
Bmax
k
Emax E
c
Bmax B
В любой момент времени отношение напряженности электрического
поля к величине магнитной индукции в электромагнитной волне
равно скорости света в вакууме
А.С. Чуев, 2020
29.
Скорость распространения электромагнитных волн в среде зависитот ее электрической и магнитной проницаемостей. Величину
n εμ
называют
абсолютным показателем преломления.
c
n
υ
и
1
υ
μ 0ε 0
1
c
με n
Показатель преломления есть физическая величина, равная
отношению скорости электромагнитных волн в вакууме к их
скорости в среде.
А.С. Чуев, 2020
30.
Электромагнитные волны – поперечные волныИзменения Е и Н синфазны!!!
Для плоской гармонической волны:
А.С. Чуев, 2020
31.
Соотношение Е/Нμμ0
E
H
εε0
Для вакуума
μ0
E
RВАК 377 Ом
H
ε0
А.С. Чуев, 2020
32.
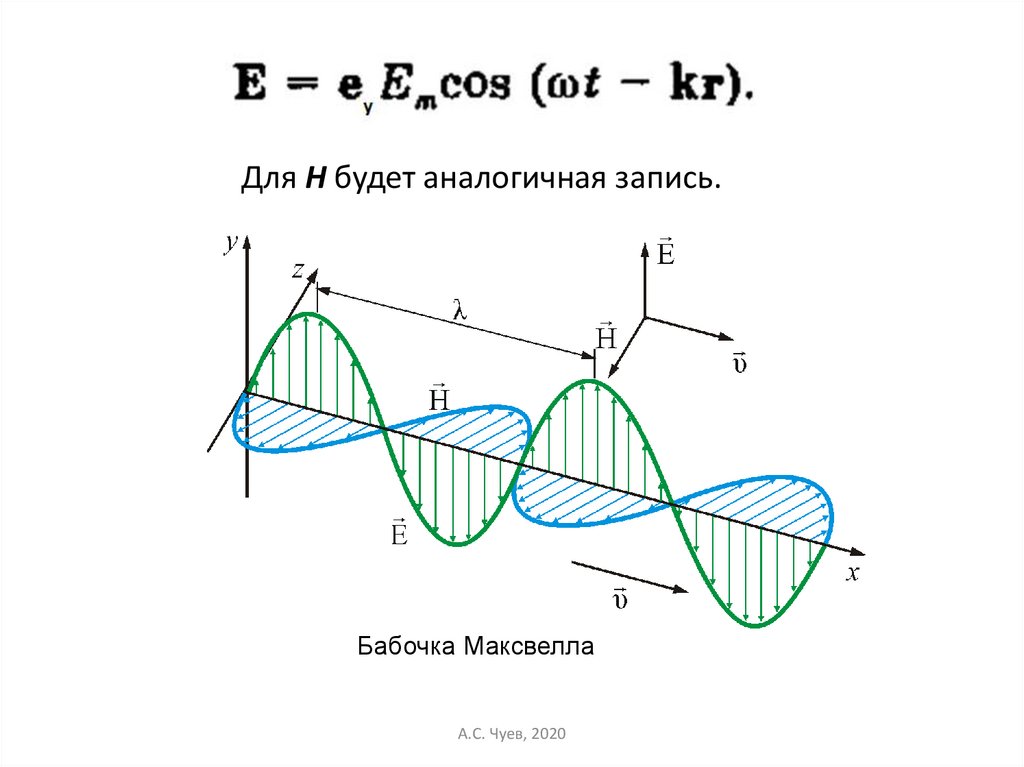
Для Н будет аналогичная запись.Бабочка Максвелла
А.С. Чуев, 2020
33.
Уравнение встречной волны:Результат наложения прямой и встречной волн:
А.С. Чуев, 2020
34.
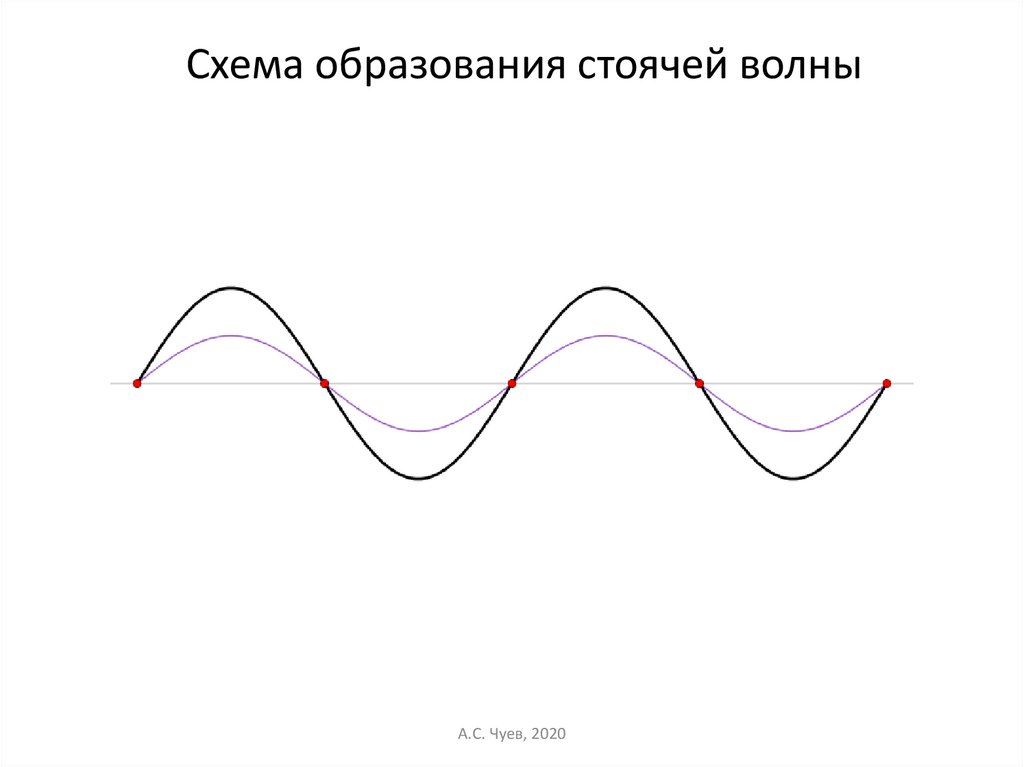
Схема образования стоячей волныА.С. Чуев, 2020
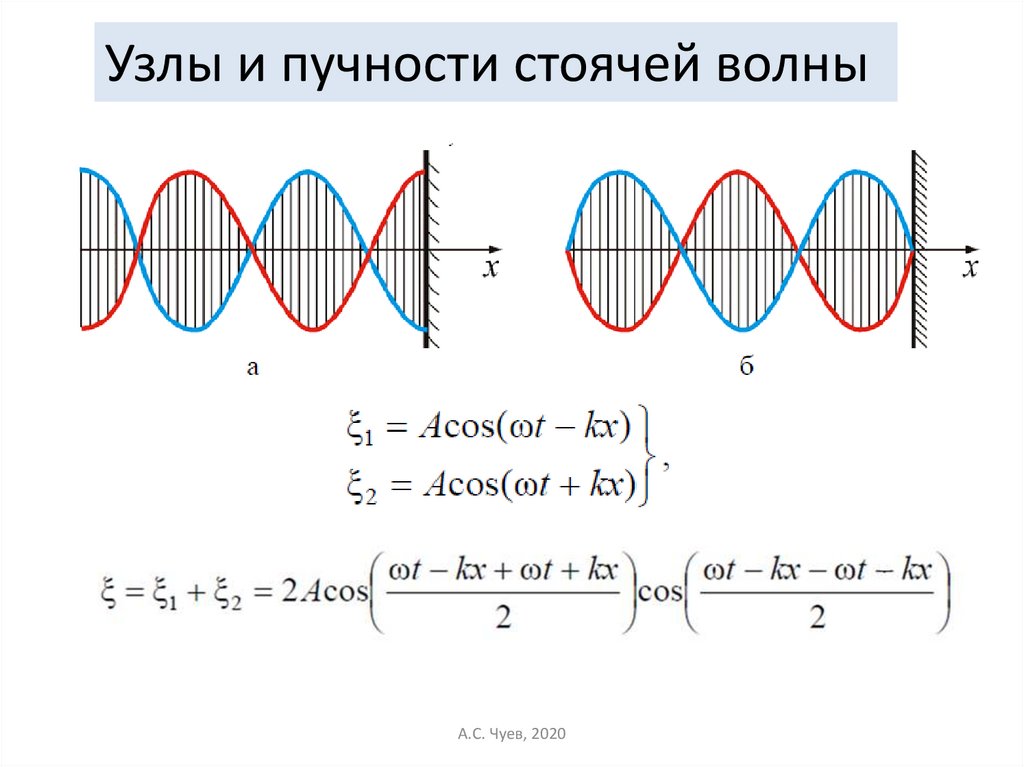
35.
Узлы и пучности стоячей волныА.С. Чуев, 2020
36.
С учетом,Уравнение стоячей волны имеет вид:
Стоячие волны не переносят энергию !!!
А.С. Чуев, 2020
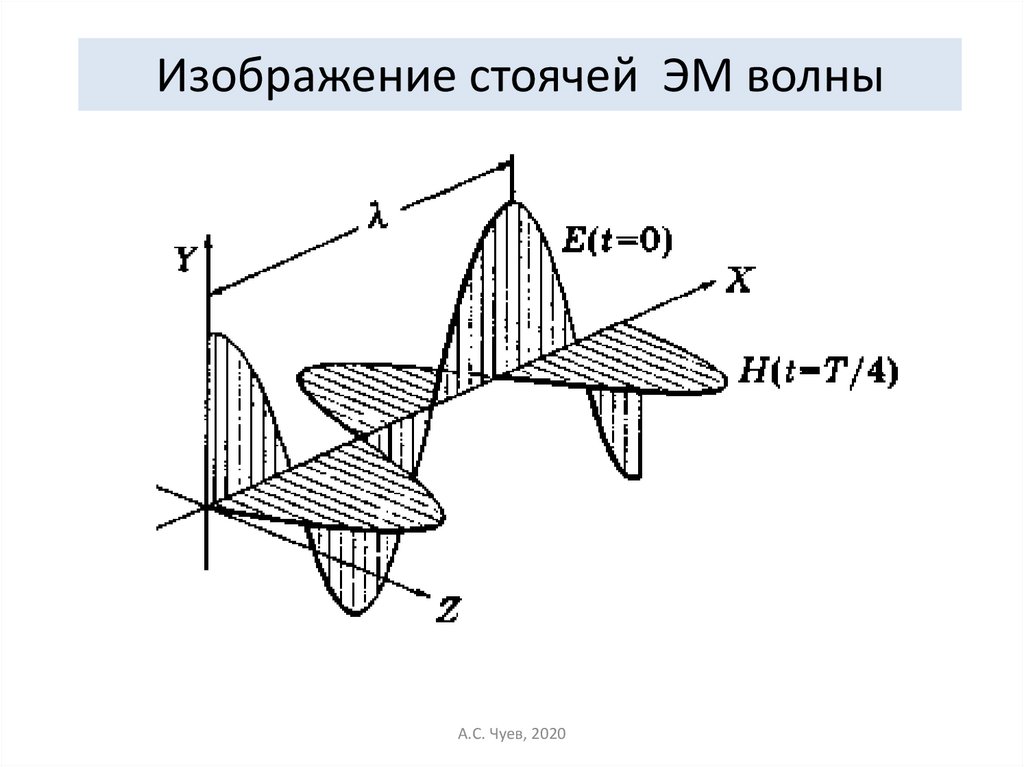
37.
Изображение стоячей ЭМ волныА.С. Чуев, 2020
38.
Используя соотношения Е с Н, можно получитьА.С. Чуев, 2020
39.
Квадрат косинуса = 1/2В результате:
А.С. Чуев, 2020
Интенсивность:
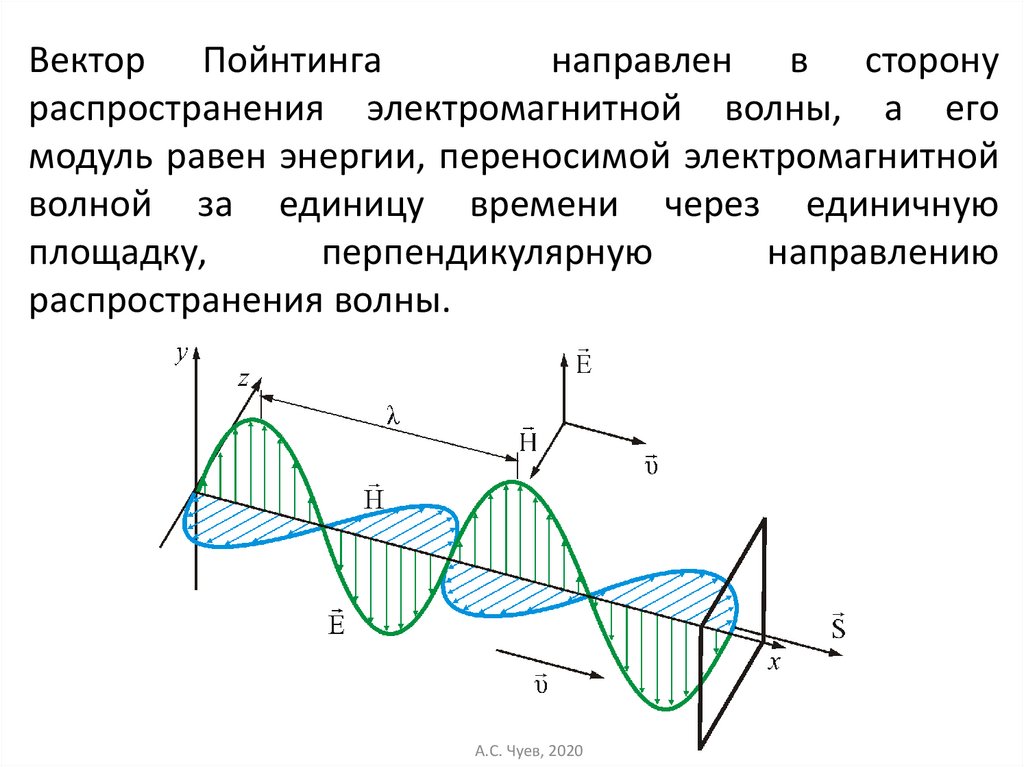
40.
Вектор Пойнтинганаправлен в сторону
распространения электромагнитной волны, а его
модуль равен энергии, переносимой электромагнитной
волной за единицу времени через единичную
площадку,
перпендикулярную
направлению
распространения волны.
А.С. Чуев, 2020
А.С. Чуев, 2020
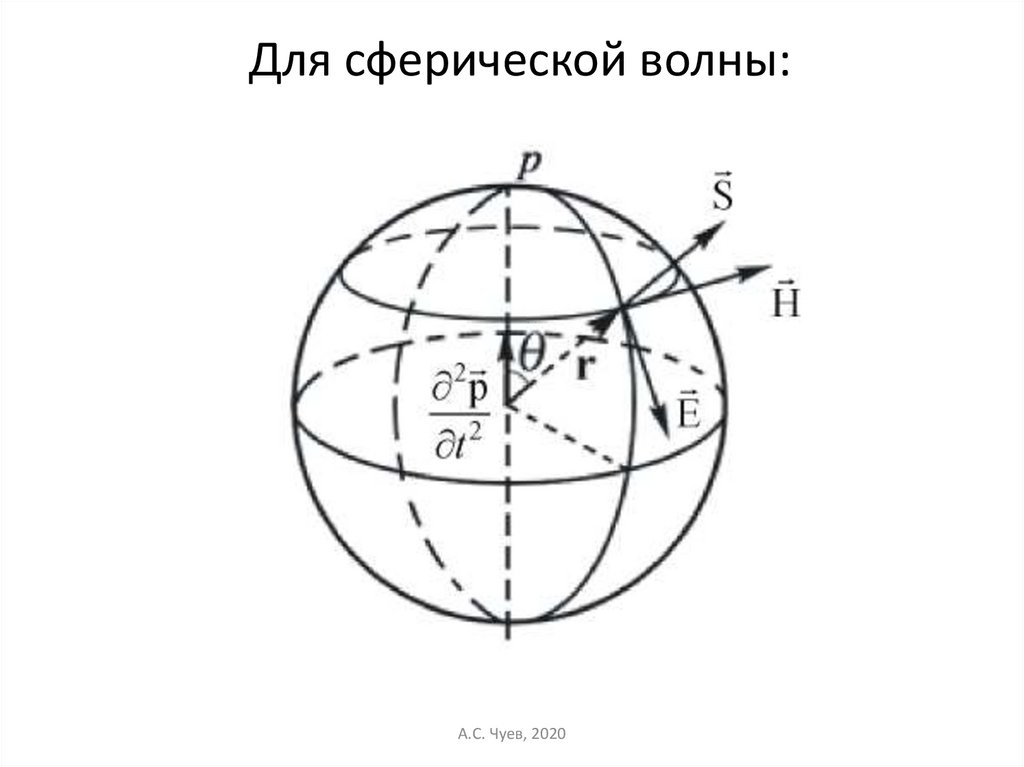
41.
Для сферической волны:А.С. Чуев, 2020
42.
Теорема ПойнтингаИз уравнений Максвелла можно получить:
D B
Преобразуем
E,
H , ( E, rotH ) ( H , rotE )
левую часть:
t
t
D B εε 0 μμ0 w
E,
H,
( E, E )
(H , H )
t
t t 2
2
t
Используя векторное тождество:
div E , H ( H , rotE ) ( E , rotH )
и
S E, H
Получим уравнение баланса ЭМ энергии, переносимой ЭМ волной:
w
div S 0
t
А.С. Чуев, 2020
43.
Это уравнение похоже на уравнение непрерывности:где
ρ
div j 0
t
- объемная плотность электрического заряда.
Применяя формулу Гаусса-Остроградского уравнение
баланса энергии можно выразить в интегральной форме:
wdV S N d
t V
- обозначена площадь.
S N - нормальная составляющая вектора Пойнтинга.
Это соотношение называют теоремой Умова-Пойнтинга.
А.С. Чуев, 2020
44.
σ- удельная проводимостьА.С. Чуев, 2020
45.
Импульс электромагнитной волныУмножив числитель и знаменатель на скорость света, получим:
А.С. Чуев, 2020
46.
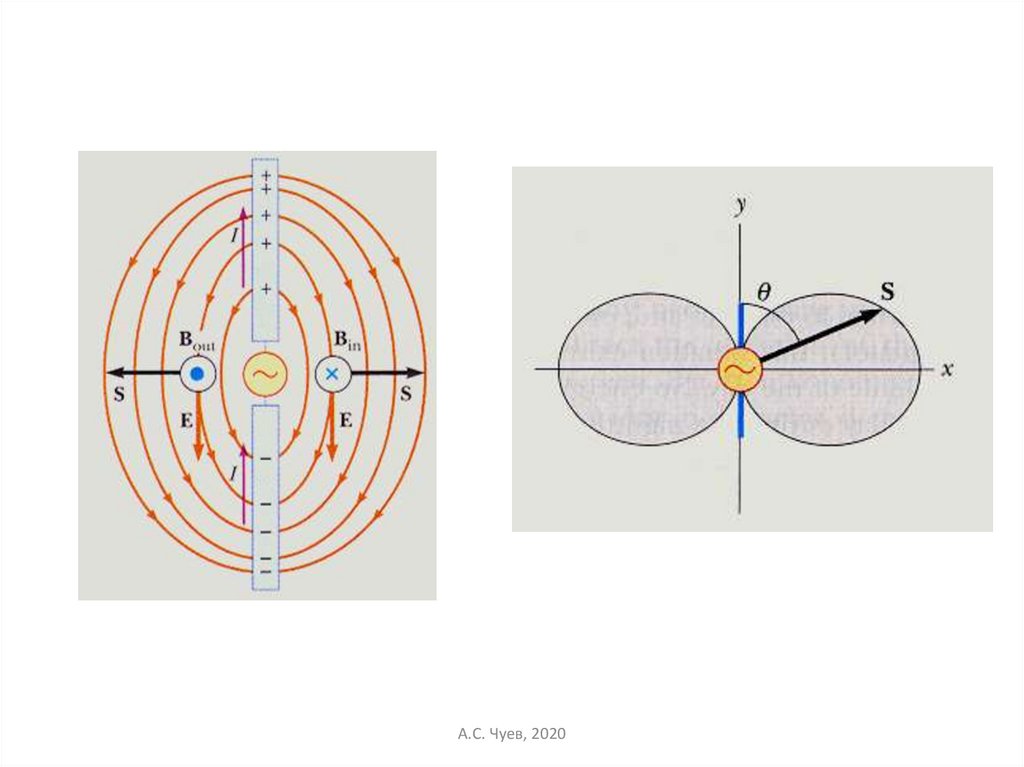
Излучение диполяА.С. Чуев, 2020
47.
А.С. Чуев, 202048.
ДалееФакультативный материал
А.С. Чуев, 2020
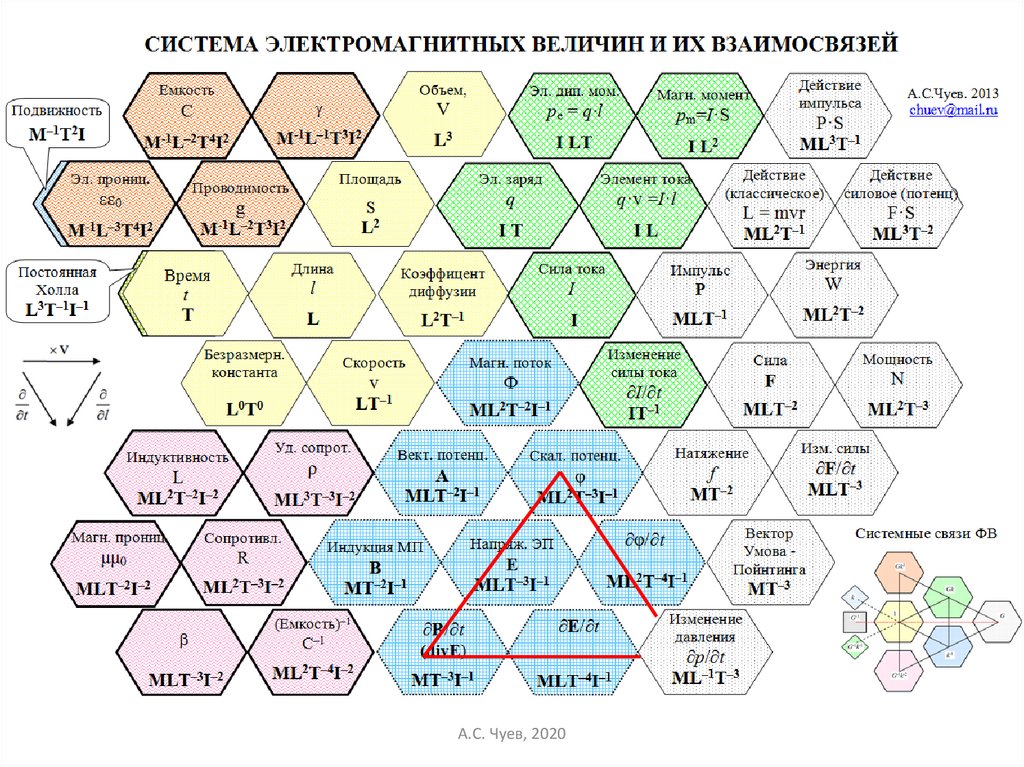
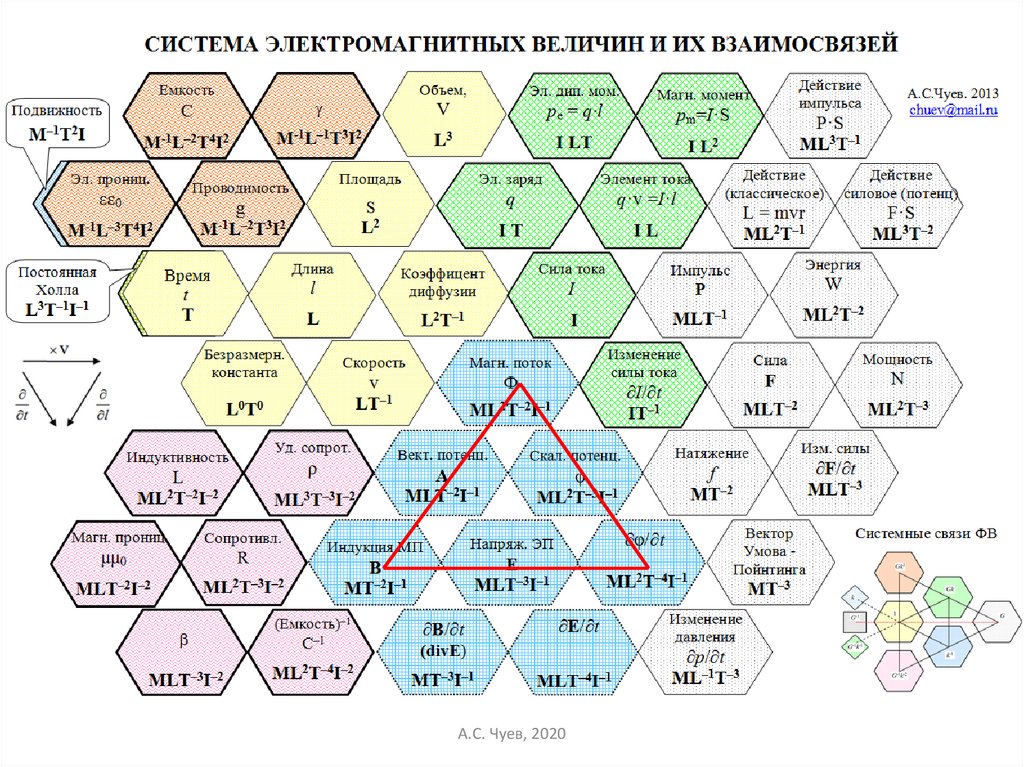
49.
Выражение полевых электромагнитныхвеличин через «материальные»
А.С. Чуев, 2020









































 Физика
Физика