Решение уравнения с модулем

1.

2.

3.

•Знать определение уравнения
и неравенства, содержащего
модуль;
•Понимать алгоритм решения
уравнений и неравенств с
модулем;
•Стимулировать учащихся к
овладению рациональными
приемами и методами
решения.
Образовательная
•Развивать логическое
мышление, память;
•Вырабатывать умения
анализировать и сравнивать;
•Уметь делать выводы и
грамотно выражать свои
мысли.
Развивающая
•Развивать коммуникативные
качества;
•Воспитывать чувство
ответственности за результаты
собственной деятельности;
•Развивать навыки контроля и
самоконтроля.
Воспитательная

4.

5.

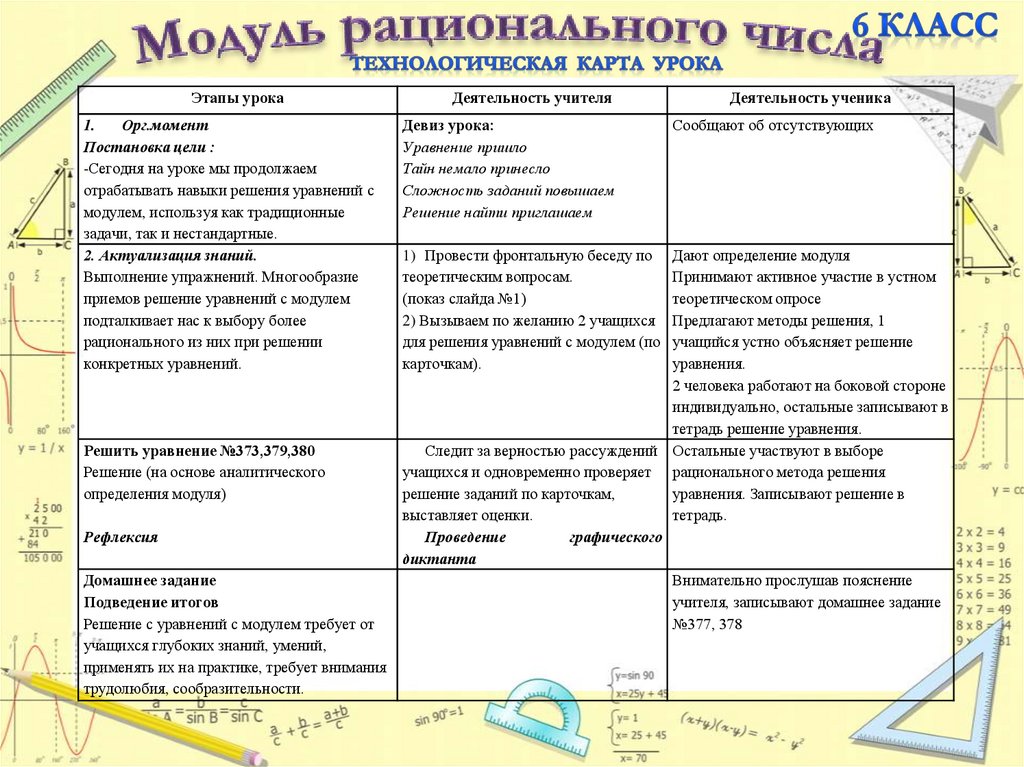
Этапы урока
1.
Орг.момент
Постановка цели :
-Сегодня на уроке мы продолжаем
отрабатывать навыки решения уравнений с
модулем, используя как традиционные
задачи, так и нестандартные.
2. Актуализация знаний.
Выполнение упражнений. Многообразие
приемов решение уравнений с модулем
подталкивает нас к выбору более
рационального из них при решении
конкретных уравнений.
Решить уравнение №373,379,380
Решение (на основе аналитического
определения модуля)
Рефлексия
Домашнее задание
Подведение итогов
Решение с уравнений с модулем требует от
учащихся глубоких знаний, умений,
применять их на практике, требует внимания
трудолюбия, сообразительности.
Деятельность учителя
Девиз урока:
Уравнение пришло
Тайн немало принесло
Сложность заданий повышаем
Решение найти приглашаем
1) Провести фронтальную беседу по
теоретическим вопросам.
(показ слайда №1)
2) Вызываем по желанию 2 учащихся
для решения уравнений с модулем (по
карточкам).
Деятельность ученика
Сообщают об отсутствующих
Дают определение модуля
Принимают активное участие в устном
теоретическом опросе
Предлагают методы решения, 1
учащийся устно объясняет решение
уравнения.
2 человека работают на боковой стороне
индивидуально, остальные записывают в
тетрадь решение уравнения.
Следит за верностью рассуждений Остальные участвуют в выборе
учащихся и одновременно проверяет рационального метода решения
решение заданий по карточкам,
уравнения. Записывают решение в
выставляет оценки.
тетрадь.
Проведение
графического
диктанта
Внимательно прослушав пояснение
учителя, записывают домашнее задание
№377, 378

6.

-2
-1
0
1
2

7.

1
1
1) 3 3
2
2
2) Модулем числа называют расстояние в единичных отрезках
от начала отчета до точки на координатной прямой,
соответствующей этому числу.
3) x 5
x1 5, x2 5
4) 2 * 52 104
5) x 11
x1 11, x2 11

8.

6) Неравенство x 5 можно записать в виде -5<x<5
7) 3,5 4 7,5
8)( 3,5) ( 4) 7,5
9) 3,5 4 7,5
10) x 6
x 6, x 6

9.

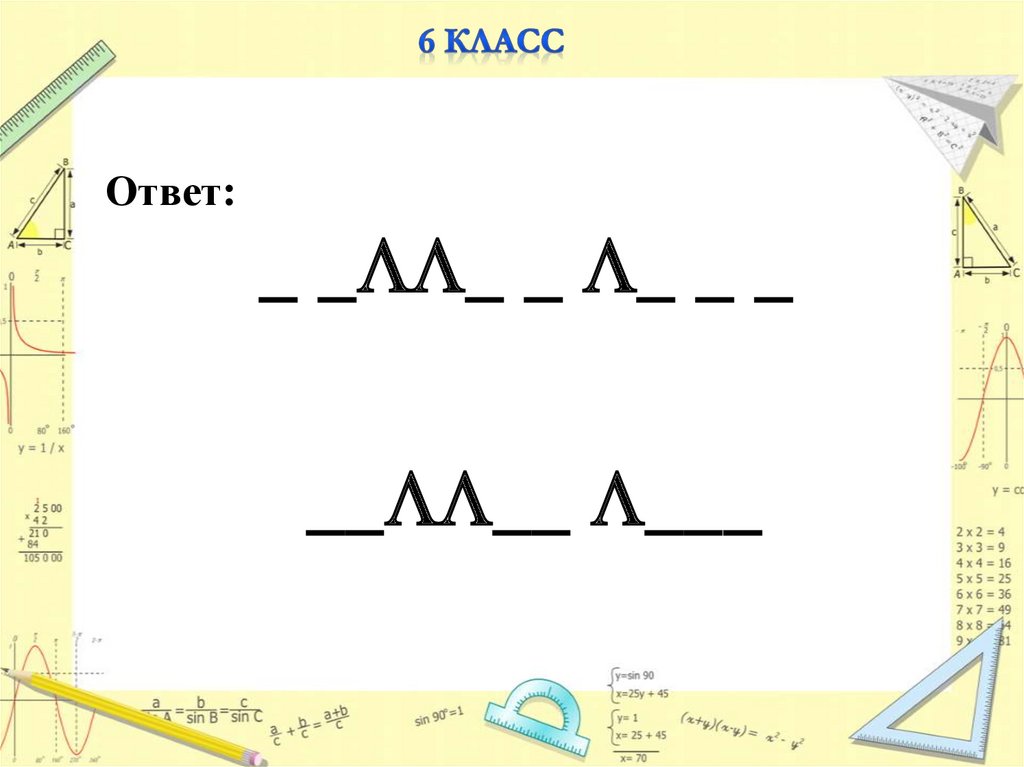
Ответ:
_ _ _ _ _ _ _
__ __ ___

10.

11.

12.

x2-2|x|=0
Решение одного уравнения несколькими методами:
1) Метод разложения на множители
|x|=x, x≥0
x2-2x=0
x(x-2)=0
x=0, x=2
x<0, x2+2x=0
x(x+2)=0
x=0, x=-2
2) Метод введения новой переменной
Пусть |x|=t, тогда уравнение примет вид:
t2-2t=0
t=0, t=2
|x|=0
|x|=2
x=0
x=-2, x=2

13.

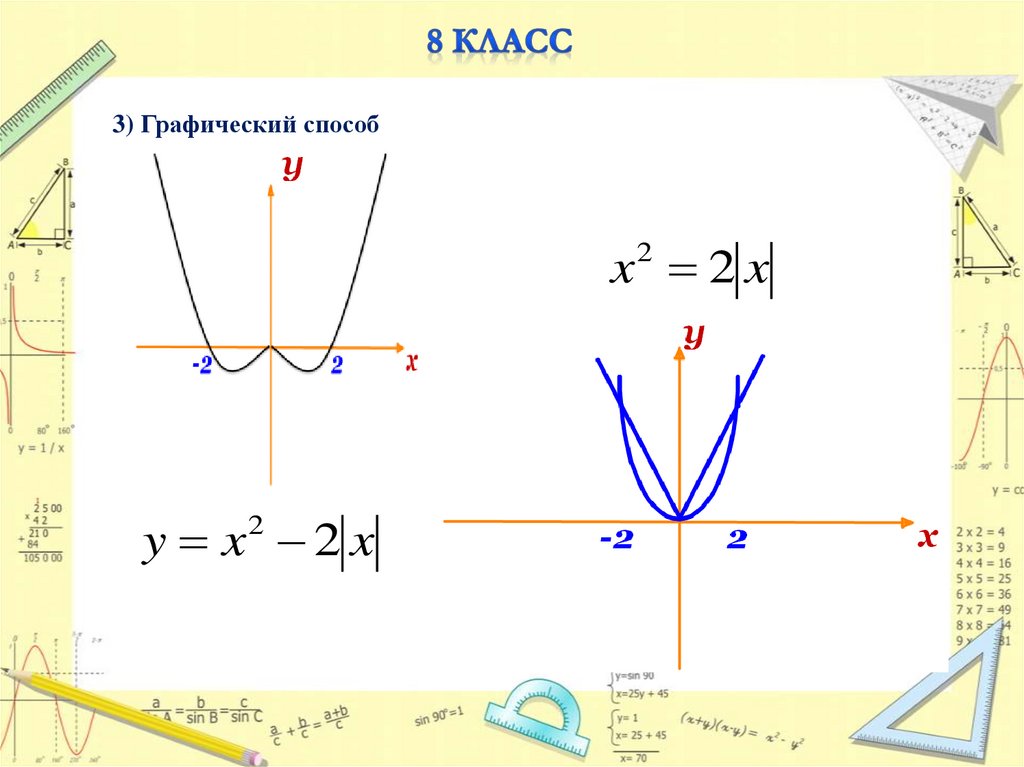
3) Графический способ
x2 2 x
y x 2x
2

14.

ТЕСТОВЫЕ ЗАДАНИЯ по теме «Решение уравнений с модулем».
1. Какие числа являются решениями уравнения |х+3|= -4?
а) -7; б) -7; 1; в) нет корней; г) 1.
2. Решите уравнение |х+3|=7:
а) 7; б) -4; в) 10; -4; г) 4; -10.
3. Определите координаты точки пересечения графиков функций у=|2х+1| и
у=0:
а) (0;0); б) (-0,5;0); в) (0;-0,5); г) (0,5;0).
4. Решите уравнение |х+3|+|х-1|=6:
а) 3; -2; б) 4; -2; в) -4; 2; г) 2; -3.
5. Сколько точек пересечения имеют графики функций у=||5,5х-4|+2| и у=3?
а) 1; б) 2; в) 3; г) 4.
6. Решите уравнение |3х-7|=1-х:
а) 2; 3; б) -2; 3; в) -3; 2; г) -2; -3.
7. Сколько решений имеет уравнение (2,5х-5)2=(0,5х-6)2:
а) 1; б) 2; в) 3; г) 4.

15.

Ответы к тестам
1. Какие числа являются решениями уравнения |х+3|= -4?
а) -7; б) -7; 1; в) нет корней; г) 1.
2. Решите уравнение |х+3|=7:
а) 7; б) -4; в) 10; -4; г) 4; -10.
3. Определите координаты точки пересечения графиков функций у=|2х+1| и
у=0:
а) (0;0); б) (-0,5;0); в) (0;-0,5); г) (0,5;0).
4. Решите уравнение |х+3|+|х-1|=6:
а) 3; -2; б) 4; -2; в) -4; 2; г) 2; -3.
5. Сколько точек пересечения имеют графики функций у=||5,5х-4|+2| и у=3?
а) 1; б) 2; в) 3; г) 4.
6. Решите уравнение |3х-7|=1-х:
а) 2; 3; б) -2; 3; в) -3; 2; г)нет решения
7. Сколько решений имеет уравнение (2,5х-5)2=(0,5х-6)2:
а) 1; б) 2; в) 3; г) 4.

16.

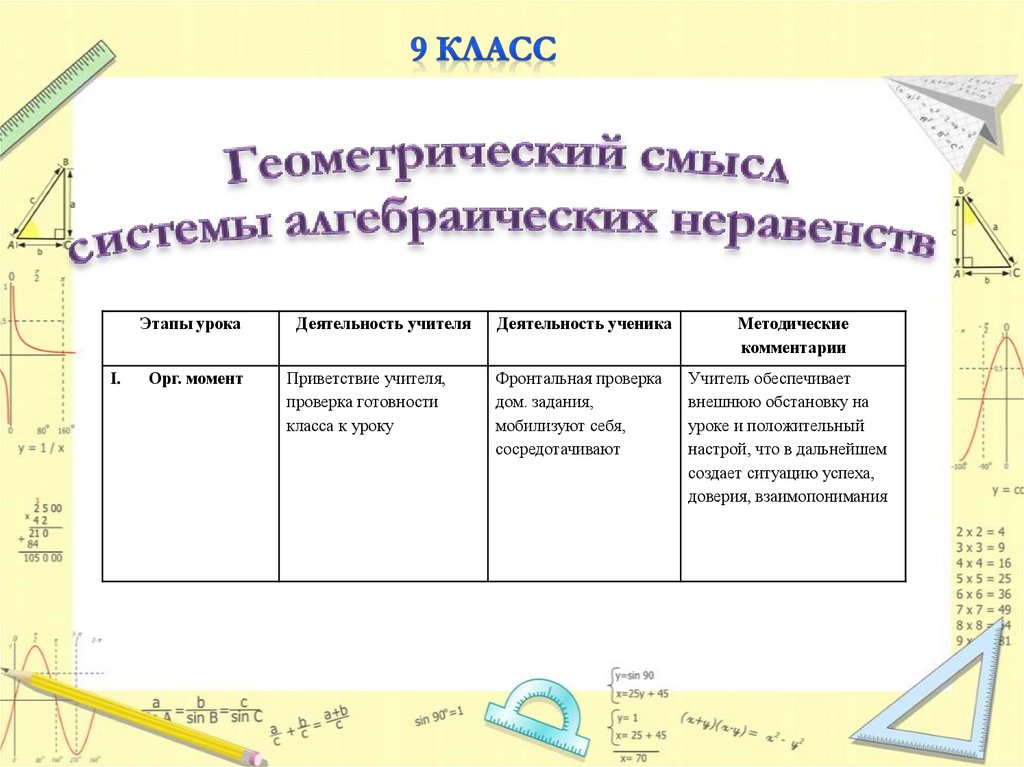
Этапы урока
I.
Орг. момент
Деятельность учителя
Приветствие учителя,
проверка готовности
класса к уроку
Деятельность ученика
Фронтальная проверка
дом. задания,
мобилизуют себя,
сосредотачивают
Методические
комментарии
Учитель обеспечивает
внешнюю обстановку на
уроке и положительный
настрой, что в дальнейшем
создает ситуацию успеха,
доверия, взаимопонимания

17.

ІІ. Актуализация
знаний
Предлагает учащимся задания,
необходимые для введения и
обоснования способа решения
неравенств с модулем. Формирует у
каждого учащегося личные
потребности в последующей
деятельности, связанной с
открытием алгоритма решений
модульного неравенства через
конкретную учебно-практическую
задачу.
Выполняют
задания, применяя
определения модуля
и свойства
неравенств.
Анализируют
затруднения ,
возникшие с
решением задач, т.е.
пытаются отделить
знания от незнания.
|x|+|y|≥3
y<
y≥x2+1
-2≤x≤3
ІІІ. Постановка цели с
опорой на
субъективный опыт
учащихся
х2+y2≤16
Учитывая учебный математический
опыт учащихся, задает вопрос: если
нужно решить систему неравенств,
как вы выйдете из сложившейся
ситуации?
Формируют цель
своей работы на
уроке, осмысливая
ее.
Использование
проблемной ситуации –
побуждения учащихся к
сравнению, обобщению,
выводам,
сопоставлению фактов.

18.

IV. Фронтальная
работа по созданию
алгоритма решения
модульных неравенств,
анализ и уточнения.
Предлагает упражнения
для фронтальной
работы по созданию
алгоритма
|y|≤x2+1
|x|≤y2+1
Предлагает работу в
парах, консультацию
|y|≤x2+1
|x|≤y2+1
Осуществляет
пооперационный
контроль за
выполнением действий
учащихся.
Вырабатывают свои
варианты решения
неравенств модулем.
Обсуждают их, приходят
к выводу о
необходимости
составить единый
алгоритм решения
Выполняют
предложенные задания
по составлению
алгоритма.
Проверяют
правильность
выполнения задания
(взаимопроверка).
Создание проблемной
ситуации о
необходимости
наличия единого
алгоритма решения

19.

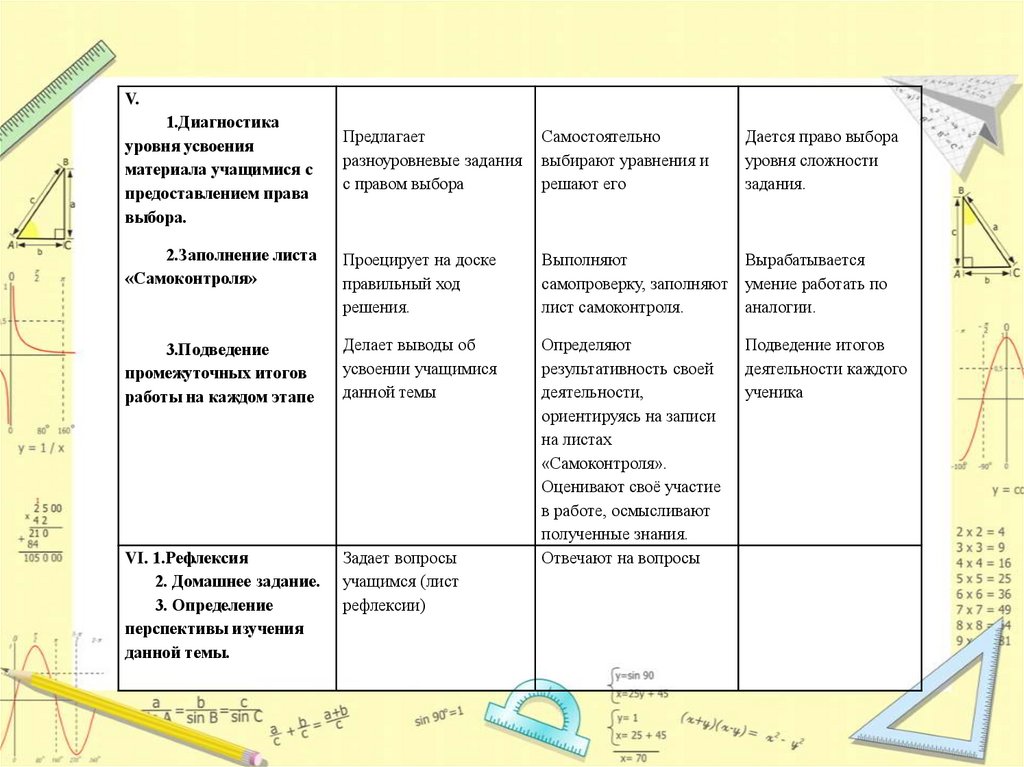
V.
1.Диагностика
уровня усвоения
материала учащимися с
предоставлением права
выбора.
Предлагает
разноуровневые задания
с правом выбора
Самостоятельно
выбирают уравнения и
решают его
Дается право выбора
уровня сложности
задания.
2.Заполнение листа
«Самоконтроля»
Проецирует на доске
правильный ход
решения.
Выполняют
Вырабатывается
самопроверку, заполняют умение работать по
лист самоконтроля.
аналогии.
3.Подведение
промежуточных итогов
работы на каждом этапе
Делает выводы об
усвоении учащимися
данной темы
VI. 1.Рефлексия
2. Домашнее задание.
3. Определение
перспективы изучения
данной темы.
Задает вопросы
учащимся (лист
рефлексии)
Определяют
результативность своей
деятельности,
ориентируясь на записи
на листах
«Самоконтроля».
Оценивают своё участие
в работе, осмысливают
полученные знания.
Отвечают на вопросы
Подведение итогов
деятельности каждого
ученика

20.

Задания
1.
2.
3.
1.
2.
3.
Самооценка
Сравнение с
правильным решением
Раскрыть модуль.
Решить полученное
неравенство
Показать решение на
графике
Раскрыть модуль.
Решить полученное
неравенство
Показать решение на
графике
+ если уверен в правильности выполнения операции
+-если не уверен в правильности выполнения операции
-если не знаешь как выполнять данную операцию

21.

Ответьте на вопросы, выбрав один из предложенных ответов или дописав свой
собственный:
1.Получив задание «Решить неравенство с модулем», я в первую очередь :
а) вспоминаю алгоритм решения неравенство с модулем;
б) ищу похожие в классной работе;
в) свой ответ
2. Вспомнив алгоритм решения неравенств с модулем , я :
а) применяю определения модуля;
б) сразу выполняю действия;
в) свой ответ
3.На сегодняшнем занятии я :
а) понял, что знаю мало;
б) остался доволен своей математической подготовкой ;
в) часто нуждался в помощи учителя;
г) нужна консультация учителя;
д) свой ответ

22.

3 x 4
3 x 4
или
3 x 4
x 1
x 7
x 7, x 7

23.

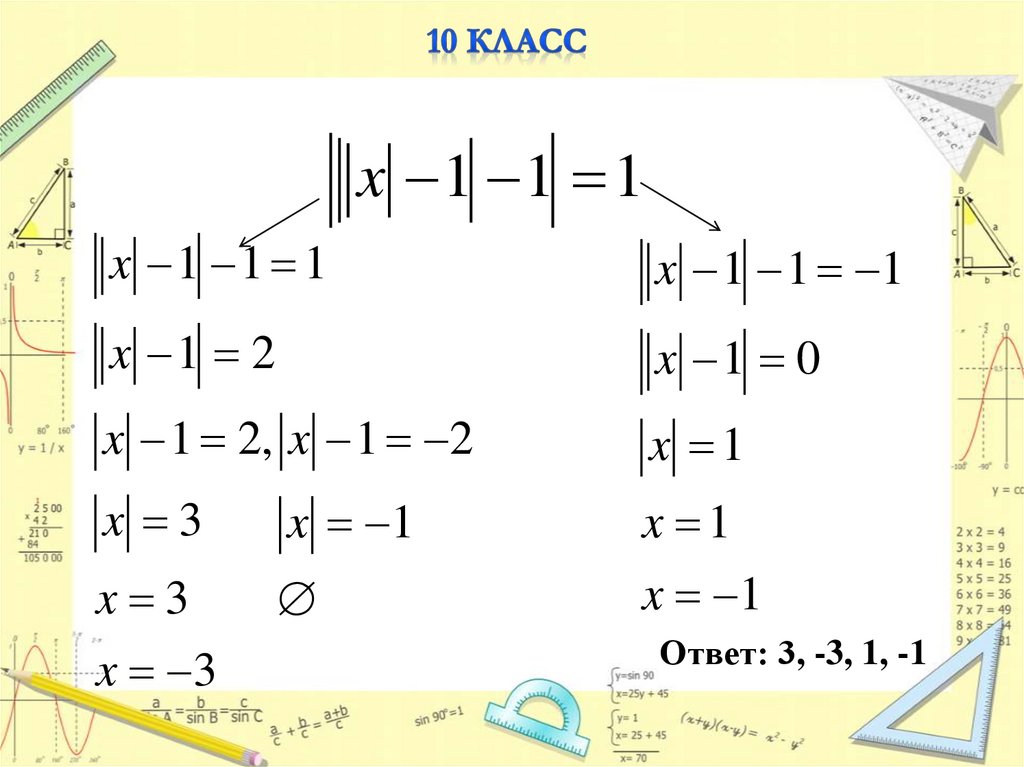
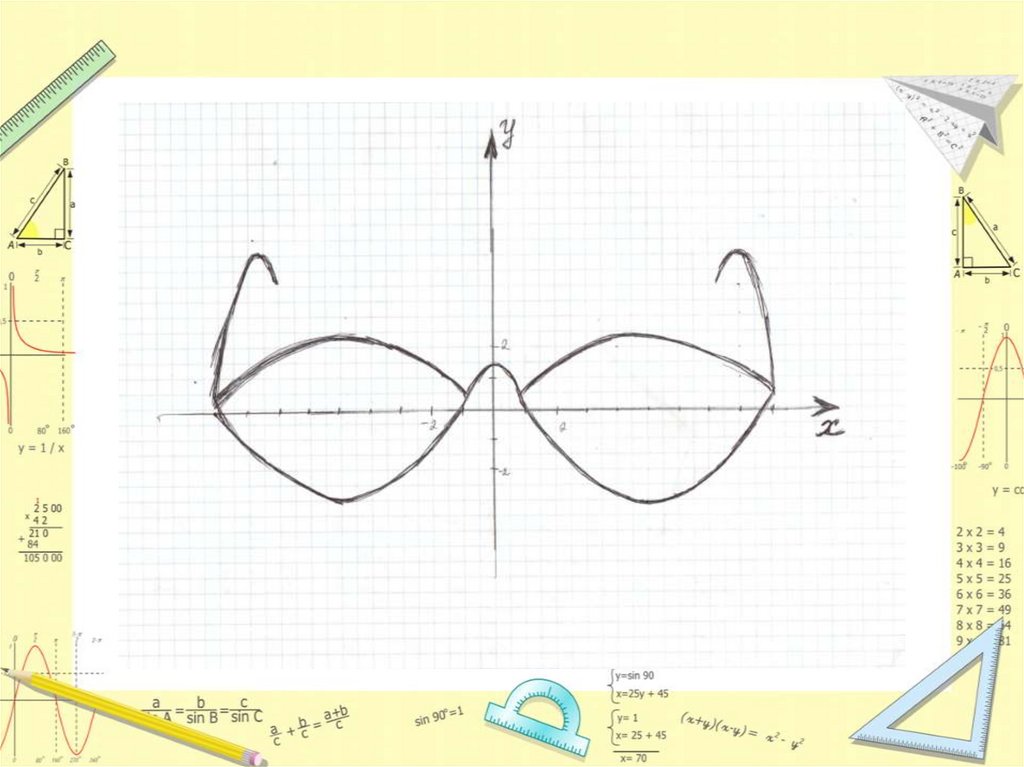
x 1 1 1
x 1 1 1
x 1 1 1
x 1 2
x 1 0
x 1 2, x 1 2
x 1
x 3
x 1
x 1
x 3
x 1
x 3
Ответ: 3, -3, 1, -1

24.

ЗАДАНИЕ С СОПУТСТВУЮЩИМИ УКАЗАНИЯМИ И ИНСТРУКЦИЯМИ
Решить уравнение |х-2|+|2х-7|=3.
Решение.
Решим уравнение методом интервалов.
1) Найдите нули подмодульных выражений, решив уравнения:
х-2=0 и 2х-7=0.
х1=… х2=…
2) Отметьте полученные значения на координатном луче.
3) Решите исходное уравнение на каждом из интервалов, предварительно определив знак
подмодульного выражения. Учитывая знак, раскрыть модули.
4) Проверьте, принадлежат ли найденные корни указанным промежуткам.
Ответ: …………………………………………………….

25.

x2 4 y 3 y 1
2x 2 y 1
1
x 4x 1 x
2
1 2x
y
2
2

26.

2x2 6x 1 0
1
x 0
2
1
y x
2
2 x 2 10 x 3 0
1
x 0
2
1
y x
2
3 7
x1
2
4 7
y1
2
5 19
x2
2
6 19
y2
2

27.

x 2 4 x 2 9 2 x 2 13
Ответ : ( ; 3 3;

28.

1
1) y
( x 5) 2 2, x 9; 1
16
1
2) y
( x 5) 2 2, x 1;9
16
1
3) y
( x 5) 2 3, x 9; 1
4
1
4) y
( x 5) 2 3, x 1;9
4
5) y ( x 7) 2 5, x 9; 6
6) y ( x 7) 2 5, x 6;9
1 2
7) y
x 1,5 , x 1;1
2

29.

30.

Вопрос
Ответ
1) Сформулируйте аналитическое определение
модуля
Вторая схема проще т. к. предполагает решение линейного
неравенства, в отличие от первой, где пришлось бы решить два
квадратных неравенства.
2) Геометрическая интерпретация модуля
1) а 0
а
а
b
b
n
6) а а n
4)
2) а а
3) аb а b
, если b 0
5)
а2 а
n Z , а2 n 2 0.
3) Перечислите свойства модуля
Разбор случаев с применением аналитического определения модуля,
применение геометрической интерпретации модуля, метод интервалов
для непрерывных функций, функционально-графический метод, метод
замены множителей, использование частных схем
4) Перечислите приёмы решений уравнений и
неравенств с модулем.
Модулем числа а называется само чиcло а,
если а >0, число (-а), если а<0, и нуль, если а=0, т.е. а b (а, b)
5) Выберите наиболее рациональную схему
для решения уравнения ; х 2 4 х 3 3 х 7
1.
f ( x) 0,
f ( x) g ( x),
f ( x) g ( x)
f ( x) 0,
f ( x) g ( x).
2.
а) Модулем числа а называется расстояние от начала отсчёта до точки
с координатой а.
б) Модуль разности чисел а и b есть расстояние между точками а и b
числовой оси, т. е.
g ( x) 0,
f ( x) g ( x) f ( x) g ( x),
f ( x) g ( x).
а, если a 0,
а 0, если а 0,
а, если а 0.