Решение уравнений и неравенств, содержащих модуль

1. Решение уравнений и неравенств, содержащих модуль

Урок подготовила учитель математики
ГБОУ СОШ № 476,
Колпинского района г. Санкт-Петербурга
Спиридонова Ирина Владимировна

2. Определение модуля

a, если a ≥ 0
|a|=
-a, если a<0
Модулем
действительного числа а
называется само это число,
если оно неотрицательное, и
противоположное ему
число, если данное число
отрицательно.
Из определения модуля следует:
1) |a| ≥0
2) |a|= |-a|

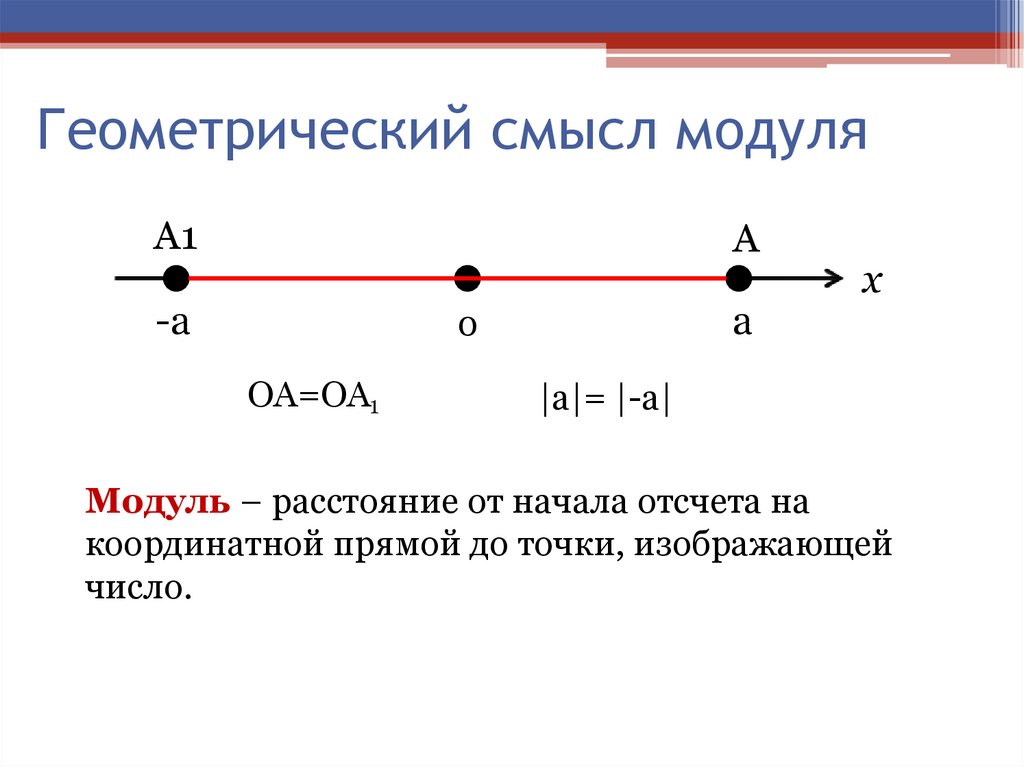
3. Геометрический смысл модуля

A1
A
-a
a
0
OA=OA1
x
|a|= |-a|
Модуль – расстояние от начала отсчета на
координатной прямой до точки, изображающей
число.

4. Устная работа

1. Найдите модуль каждого из чисел: 81, 2, 1,
-3, 6, 0, -7,4.
2. Назовите модуль какого числа равен: 7, 2,
1, 0 ,5 , 6
3. Решите уравнения:
1.
2.
3.
4.
|х|=3
|х|=0
|х|=-3
|х|=х

5. Решение уравнений

1. |х|=2,6
х=2,6 или х=-2,6
Ответ: -2,6; 2,6
2. |х+5|=3
х+5=3 или х+5=-3
х=3-5
х=-3 -5
х=-2
х=-8
Ответ: -8; -2
Решите самостоятельно:
|3х-5|=7
|6-2х|=8
|х+3|=0
|3х+2|= -3
* |х+3|+|х+1|= -5

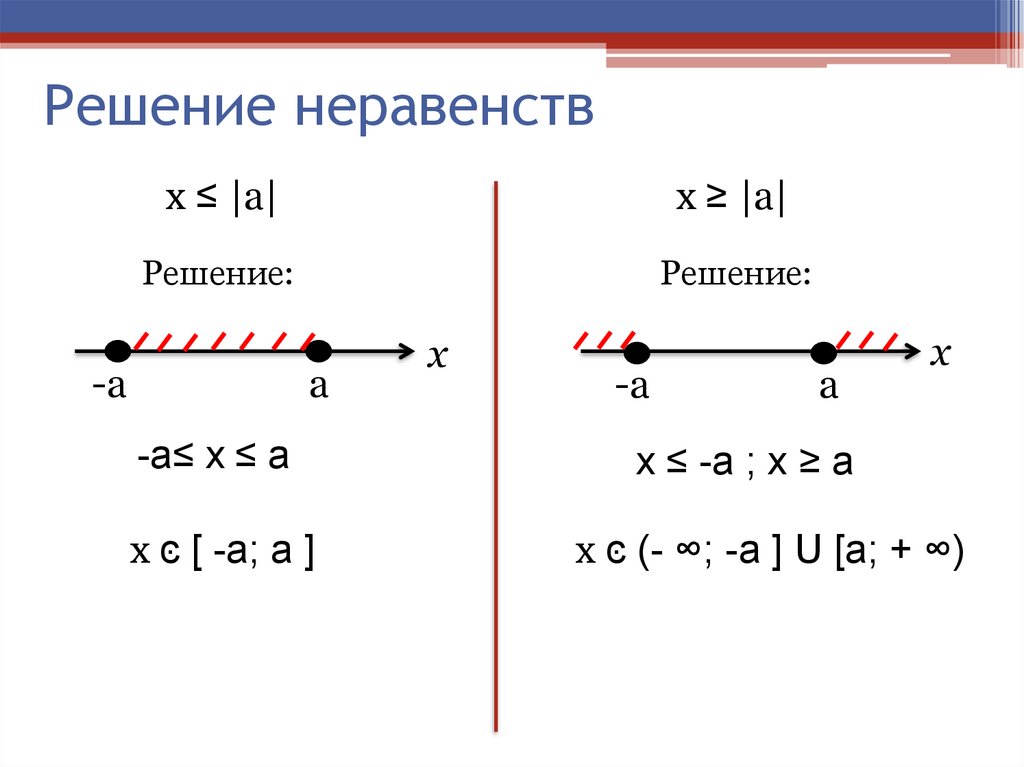
6. Решение неравенств

х ≤ |a|
х ≥ |a|
Решение:
Решение:
-a
a
-a≤ х ≤ a
x ͼ [ -a; a ]
x
-a
a
x
х ≤ -a ; x ≥ a
x ͼ (- ∞; -a ] U [a; + ∞)

7. Решите неравенства:

1.
2.
3.
4.
5.
|х|<7
|х|>6
|х-6|<5
|х+5|≥ 2
|х+1|≤ 2

8. Проверка

1. -7< х < 7
2. х<-6; х>6
3. |х-6|<5
Решение:
-5< х-6 <5
1< х-6 <11
7< х < 17
4. |х+5|>2
х+5<-2 ; х+5>2
x<-2 -5
х>2-5
х< -7
х> -3
5. |6х+1|<2
-2<6х+1<2
-3<6х<1
-1/2 <х< 1/6

9. Упражнения на «5»

На выбор:
1. Решите уравнения:
|х|+2х=3
2. Решите неравенство:
|2х|>х+3
3. Решите неравенство:
|2х|>х+3
4. При каком b верно
равенство?
а) |b|=- b
б) |b+4|=b+4
в) |b-5|=5-b
г) |6-b| =
1
b-6

10. Урок окончен, молодцы!