Решение уравнений с модулем

1. Решение уравнений с модулем

2. Содержание

1. Определение модуля
2. Виды уравнений:
f x a, a const
f x g x
f x g x
f1 x f 2 x f n x g x
3. Методы решения уравнений
4. Задания для самостоятельного решения
5. Выводы
6. Домашнее задание

3.

Большинство уравнений с модулем можно решить исходя из
определения модуля:
a, если a 0,
a
- a, если a 0
Пример
Содержание

4.

Пример 1
Решить уравнение
2x 5 x
Решение:
x 2,5
2 x 5 0
x 5
x 5
2 x 5 x
x 2,5
5
2x 5 x
x
2 x 5 0
3
5
x
3
2 x 5 x
Ответ:
5
,5
3
Методы решения
Содержание

5.

Пример 2
Решить уравнение
x 2 1 2 x 1
Если решать это уравнение по определению, то
придется трижды использовать определение модуля
и при этом нам необходимо будет решить 8 систем.
Поэтому, чтобы избежать этих сложностей, полезно
знать ряд равносильных преобразований некоторых
типов уравнений и другие способы решения
уравнений.

6.

Уравнение вида:
f x a, a const
Равносильно :
, если a 0
f ( x ) 0, если a 0
f ( x) a
f ( x ) a, если a 0
Пример
Содержание

7.

Пример 3
Решить уравнение
x 2 3x 2 1
Решение:
x 3x 2 1
x 3x 3 0;
x 3x 2 1 2
2
x 3x 2 1 x 3x 1 0
2
2
Ответ:
2
3 21
x
2
3 13
x
2
3 21 3 13
,
2
2
Заметим, что если бы мы решали уравнение по определению,
то у нас возникли бы затруднения при подстановке корней в
соответствующие неравенства.
Следующая
равносильность
Содержание

8.

Рассмотрим уравнения вида
f x g x
Такие уравнения можно решать двумя способами:
I способ:
Если f(x) имеет более простой вид, чем g(x), то
f x 0,
f x g x ,
f x g x
f x 0,
- f x g x .
Пример
Далее

9.

Пример 4
Решить уравнение
x 7 x3 15x2 x 7
Решение:
x 7 0,
3
2
x
7
x
15
x
x 7;
3
2
x 7 x 15x x 7
x 7 0,
x 7 x 3 15 x 2 x 7
x 7,
x 7,
3
3
2
2
2
x
15
x
14
0
;
x
x
14
x
1 0;
x 7,
x 7,
x x 2 15 x 2 0
x 3 15 x 2 2 x 0

10.

Решим уравнение первой системы:
x
3
x 2 14 x 2 1 0
x 2 x 1 14 x 1 x 1 0 x 1 x 2 14 x 14 0
x 1; x 7 63
Решим уравнение второй системы:
x x 15x 2 0
2
15 217
x 0; x
2

11.

Вернемся к совокупности систем:
x 7,
x 1,
x 7 63,
x 7 63,
x 7,
x 0,
15 217
x
,
2
15 217
x
2
Ответ:
x 7 63,
x 0,
x 15 217
2
15 - 217
0; 7 63,
.
2
Следующая
равносильность
Содержание
Далее

12.

II способ: Если g(x) имеет более простой вид, чем f(x).
Если g(x)<0, то уравнение |f(x)|=g(x) не имеет решений
Если g(x)≥0, то
g x 0,
f x g x f x g x ,
f x g x
Пример
Содержание

13.

Пример 5
Решить уравнение
6 x 3 2 x 2 4 x 33 10 x 35
Решение:
10 x 35 0,
6 x 3 2 x 2 4 x 33 0 6 x 3 2 x 2 4 x 33 10 x 35,
6 x 3 2 x 2 4 x 33 10 x 35
Решим первое уравнение совокупности:
6 x 3 2 x 2 4 x 33 10 x 35 6 x 3 2 x 2 6 x 2 0
6 x x 2 1 2 x 2 1 0 2 x 2 1 3x 1 0
x 1,
1
x .
3

14.

Решим второе уравнение совокупности:
6 x 3 2 x 2 4 x 33 10 x 35 6 x 3 2 x 2 14 x 68 0
6 x 3 48 2 x 2 8 14 x 28 0
6 x 2 x 2 2 x 4 2 x 2 x 2 14 x 2 0
x 2 3x 2 5x 17 0 x 2
Вернемся к системе:
10 x 35 0,
x 1,
1
x 3,
x 2
Система решений не имеет, следовательно, уравнение
Следующая
Содержание
решений не имеет.
равносильность

15.

Рассмотрим уравнения вида
f x g x
Так как обе части уравнения неотрицательны, то
f x g x f
2
x g x
2
f x g x ,
f x g x f x g x 0
f x g x .
И мы получаем следующую равносильность:
f x g x ,
f x g x
f x g x .
Пример
Содержание

16.

Пример 6
Решить уравнение
x 5 6 x 2 9 x 6 x 5 2 x 3 6 x 2 13x 6
Решение:
x 5 6 x 2 9 x 6 x 5 2 x 3 6 x 2 13x 6
x 5 6 x 2 9 x 6 x 5 2 x 3 6 x 2 13x 6,
5
2
5
3
2
x
6
x
9
x
6
x
2
x
6
x
13x 6.
2 x x 4 x 2 2 0,
2 x 5 2 x 3 4 x 0,
3
3
2
2 x 6 x 2 11x 6 0.
2
x
12
x
22
x
12
0
.
Решим первое уравнение совокупности:
2 x x 4 x 2 2 0 x x 4 1 x 2 1 0
x x 2 1 x 2 1 x 2 1 0 x x 2 1 x 2 2 0
x 0,
x 2.

17.

Решим второе уравнение совокупности:
x 3 6 x 2 11x 6 0 x 1 x 2 5x 6 0
x 1,
x 2,
x 3.
Вернемся к совокупности:
x
x
x
x
x
0,
2,
1,
2,
3.
Ответ: 0, 2 , 1, 2 ,3.
Методы решения
Содержание

18.

Рассмотрим уравнения вида
f1 x f 2 x f n x g x
Для решения уравнений такого вида удобно воспользоваться
следующим алгоритмом:
1)Найти нули подмодульных выражений;
2)Провести столько параллельных прямых, сколько
содержится модулей в данном уравнении;
3)Нанести на каждую прямую знаки, соответствующие
подмодульной функции;
4)Через точки, соответствующие подмодульным нулям,
провести вертикальные прямые, которые разобьют
параллельные прямые на интервалы;
5)Раскрыть модули на каждом интервале и решить на этом
интервале уравнение.
Пример
Содержание

19.

Пример 7
Решить уравнение
x 1 2 x x 3 4
Решение:
1. Нули подмодульных выражений: x1 1, x2 2, x3 3
2. Проведем параллельные прямые, нанесем на них эти
значения и знаки, соответствующие модулям на каждом
из полученных интервалов:
I
II
III
IV
x 3
–
+
+
+
2 x
+
+
+
–
x 1
–
–
+
+
-3
-1
2
x

20.

Раскрывая модули на каждом интервале, получим
совокупность систем:
x 3,
x 3,
x
1
2
x
x
3
4
x 0
3 x 1,
3 x 1,
x 1 2 x x 3 4
x 2
x 1 2 x x 3 4
1 x 2,
1 x 2,
x 1 2 x x 3 4
x 4
x
2
,
x 2,
x 1 2 x x 3 4
x 8
x 2, x 8.
Ответ:
-2; 8
Методы решения
Содержание

21.

В некоторых случаях удобнее использовать метод замены
переменной.
Пример 8
Решить уравнение
x 2 2 2 x 2 8 0
Решение:
Данное уравнение может быть решено несколькими
способами.
Например:
Способ 1. Используя определение модуля.
Способ 2. Свести уравнение к равносильности f x g x
Способ 3. Замена переменной.
Заметим, что x 2 2 x 2 2 Замена: x 2 t, t 0
Уравнение принимает вид: t 2 2t 8 0, t1 4 (п.к.), t 2 2
Обратная замена: x 2 2 x 4, x 0
Ответ: 0; 4
Методы решения
Содержание

22.

Бывает и так , что уравнение нельзя отнести ни к одному из
рассмотренных типов, а так затруднительно решить его исходя
из определения. В этом случае удобно воспользоваться
графическим способом решения.
Пример 9
Решить уравнение
x 2 1 2 x 1
Решение:
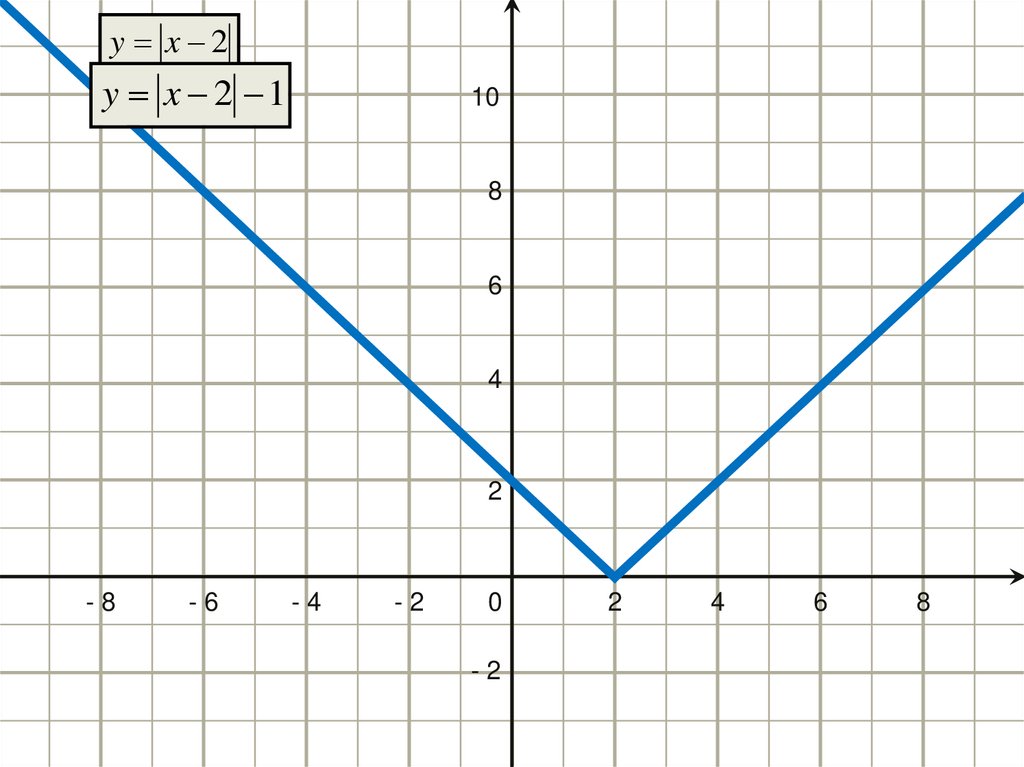
Построим в одной системе координат графики функций
y x 2 1 2, y x 1

23.

y x 2
y x 2 1
10
8
6
4
2
-8
-6
-4
-2
0
-2
2
4
6
8

24.

yy x 2 1
10
8
6
4
2
-8
-6
-4
-2
0
-2
2
4
6
8

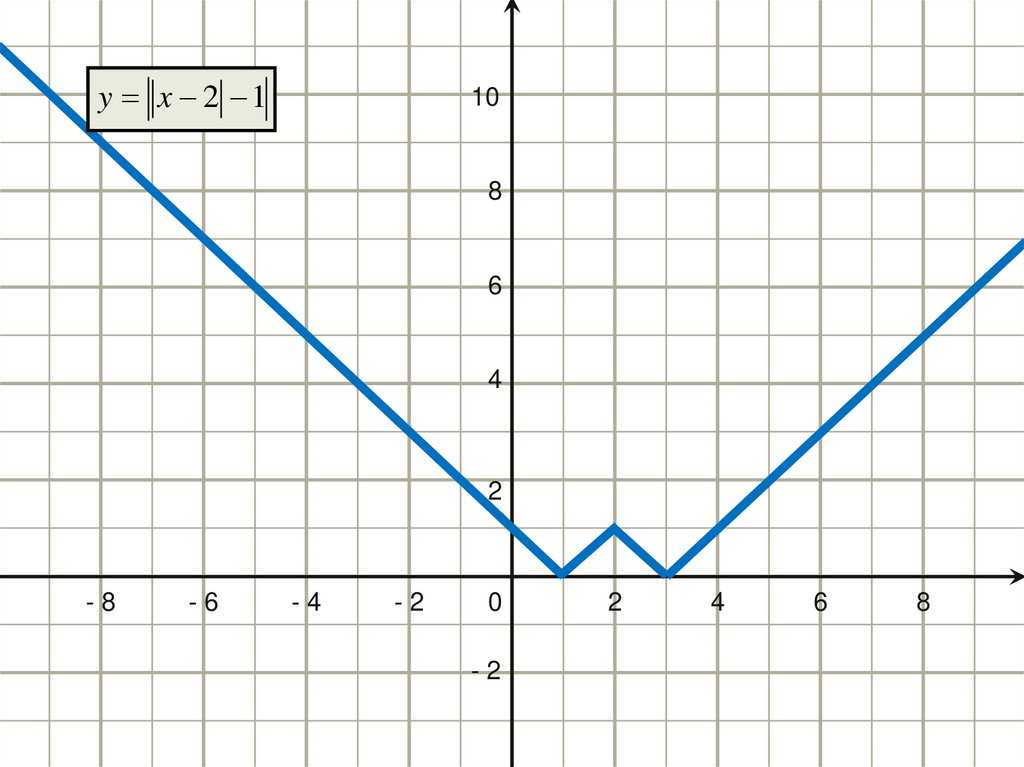
25.

10
y x 2 1 2
8
6
4
2
-8
-6
-4
-2
0
-2
2
4
6
8

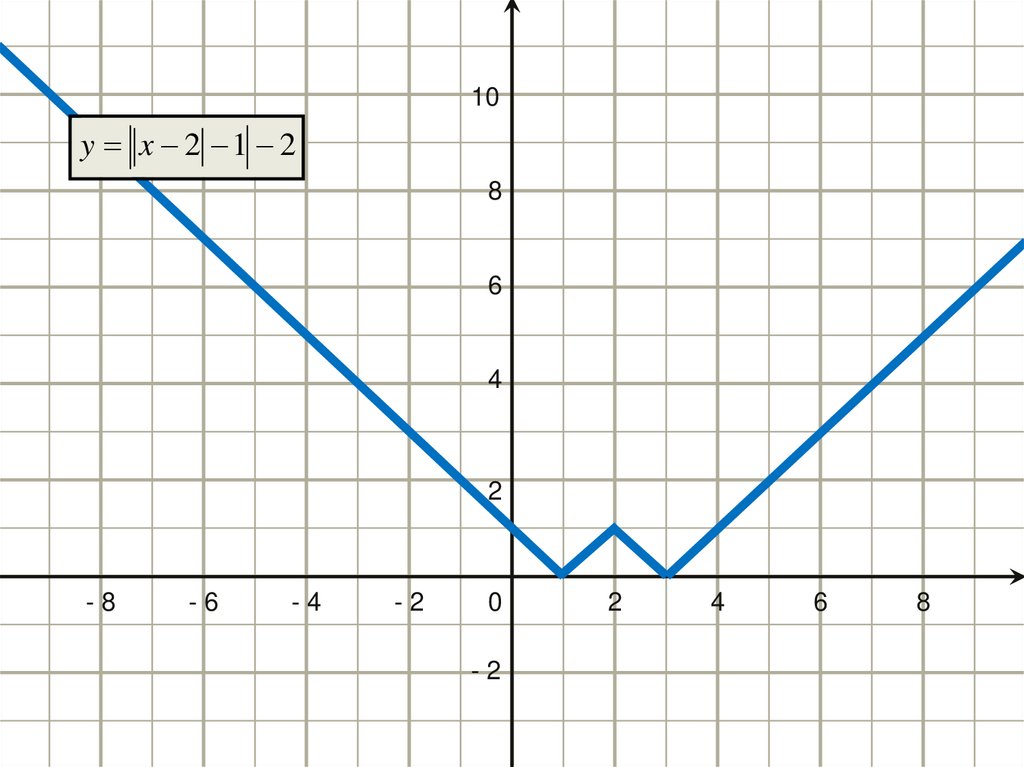
26.

10
y x 2 1 2
8
6
4
2
-8
-6
-4
-2
0
-2
2
4
6
8

27.

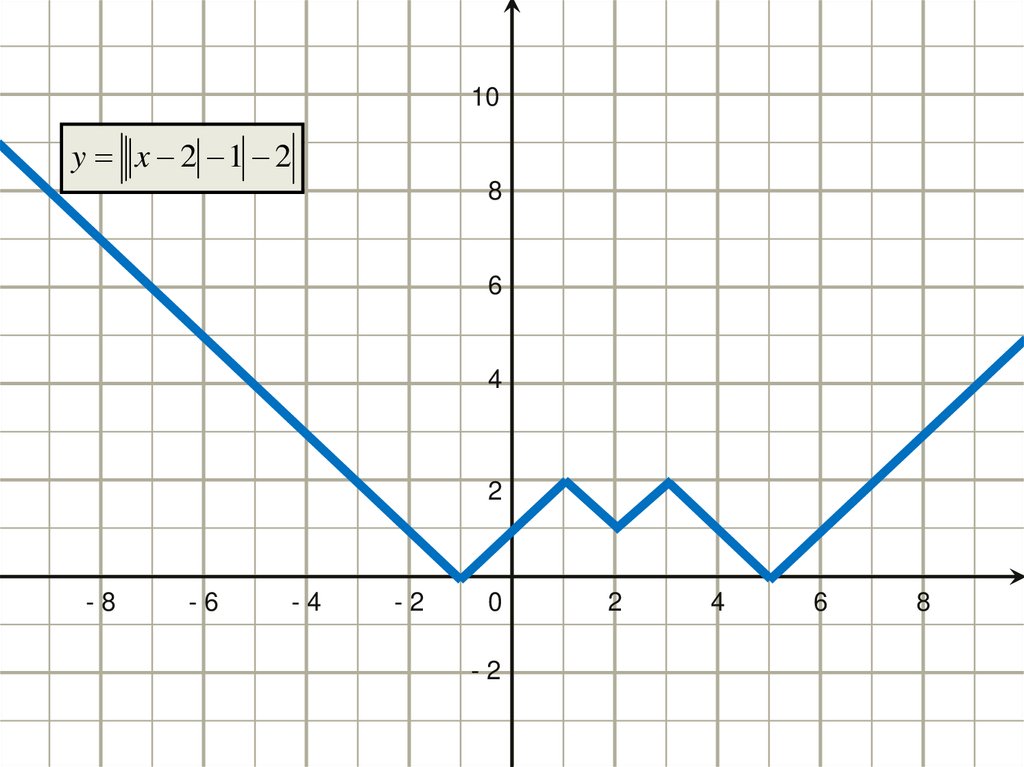
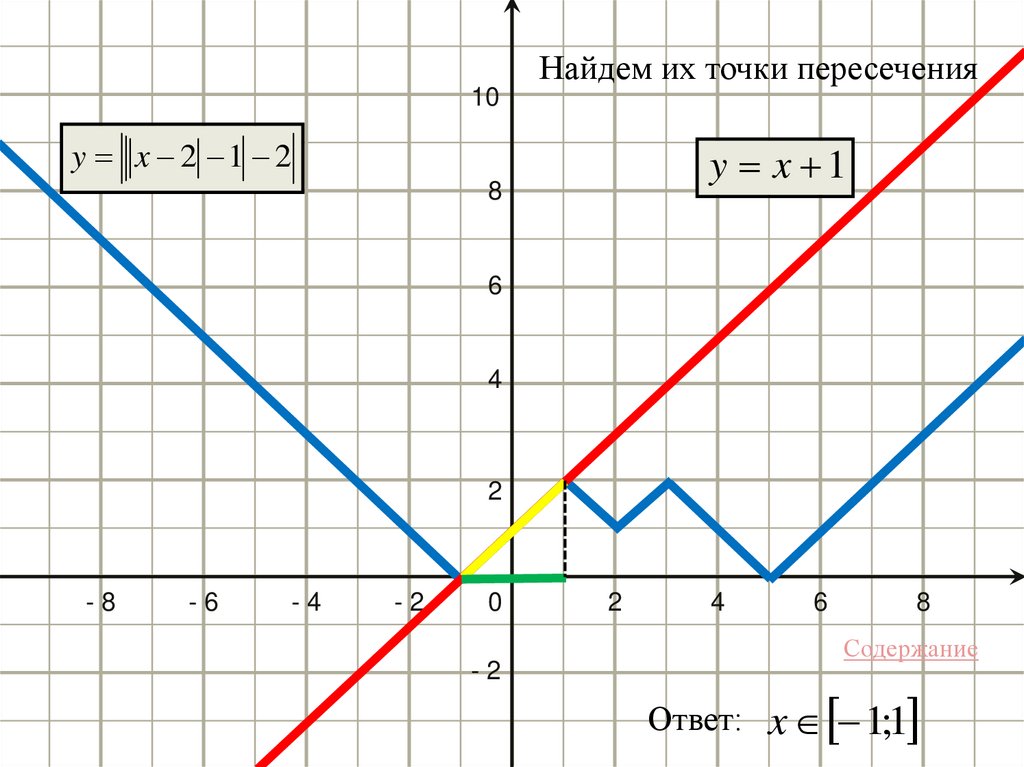
Найдем их точки пересечения
10
y x 2 1 2
y x 1
8
6
4
2
-8
-6
-4
-2
0
2
4
6
8
Содержание
-2
Ответ:
x 1;1

28. Задания для самостоятельного решения:

1) x 2 6x x 4 8 0
Ответ : 3; 4.
2) x 2 x 1 1
Ответ : 0; 1; 2.
3) x 2 x 3 x
Ответ : 1; 3 .
4) x 2 x 3 2x 8 9
Ответ : 1; 5,5.
5) x - x 2 1 2x - 3 - x 2
Ответ : 2.
6) x 1 - 2 x 1 1 0
Ответ : - 2; 0.
7) x 2 2x - 3 x 1 3 0
Ответ : - 3; - 2; 0;1.
2
Содержание

29. Выводы

1. Виды уравнений:
f x a, a const
f x g x
f x g x
f1 x f 2 x f n x g x
2. Методы решения уравнений
Аналитический:
- по определению
- использование равносильностей
- разбиение на промежутки
- замены переменной
Графический
Содержание

30. Домашнее задание

Уровень 1
Уровень 2
1) x - 1 2 x 1 1 0
1) x x 6
2
2
2) x 1 1 x
2
2
2) x 2 x 8 x
3) x 2 x - 6 0
3) x 10 2 x 10 11
4) 2 x 1 x 3
4) 3 - x 2x 2 3
5) x - 1 x 1 4
5) x 2 4x 3 x 2 5x 4 0

31. Уровень 3

1) 2x 1 1 5p
2) 2x - x 3 x 7
2
3) x 2 4 9 x 2 5
4)
9 - x 2 x 2 4x 3
5) x 2 2x 3 x 2 2x 8 4x 5
Содержание