Похожие презентации:
Усеченная пирамида
1.
Усеченная пирамида2.
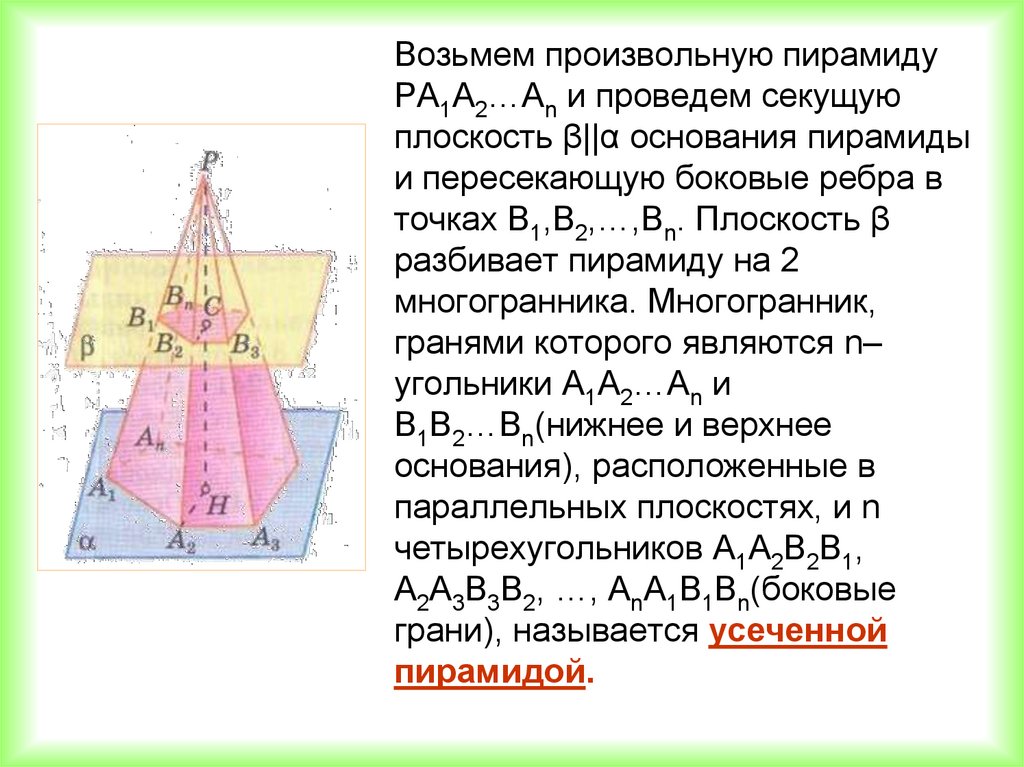
Возьмем произвольную пирамидуPA1A2…An и проведем секущую
плоскость β||α основания пирамиды
и пересекающую боковые ребра в
точках B1,B2,…,Bn. Плоскость β
разбивает пирамиду на 2
многогранника. Многогранник,
гранями которого являются n–
угольники A1A2…An и
B1B2…Bn(нижнее и верхнее
основания), расположенные в
параллельных плоскостях, и n
четырехугольников A1A2B2B1,
A2A3B3B2, …, AnA1B1Bn(боковые
грани), называется усеченной
пирамидой.
3.
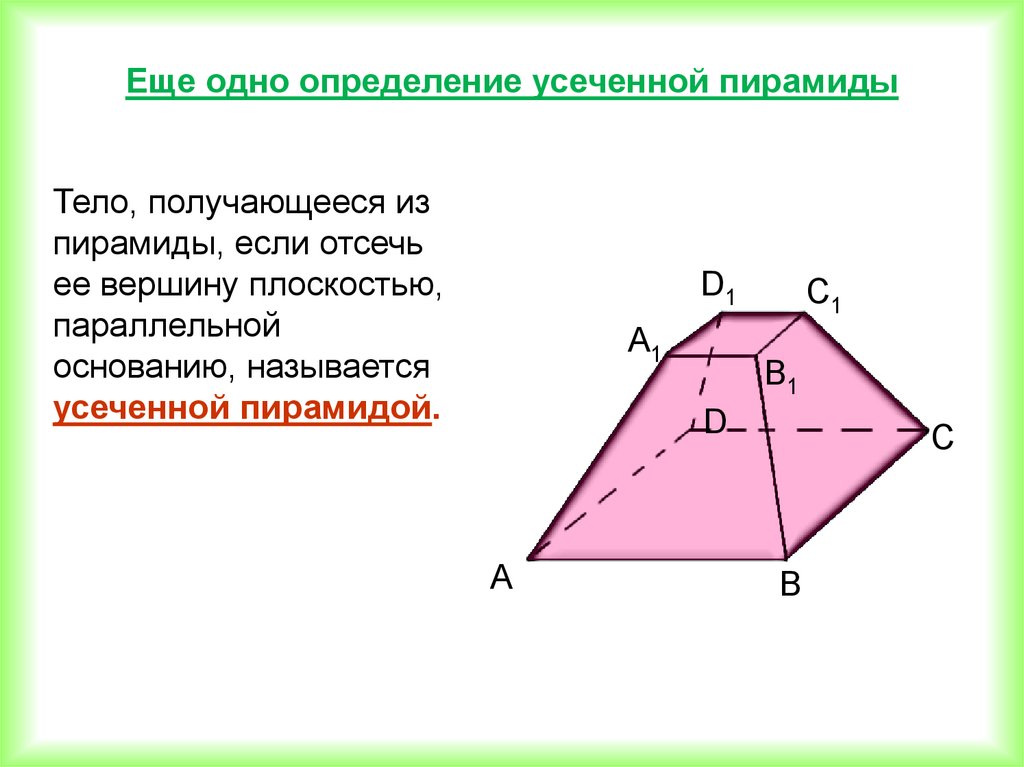
Еще одно определение усеченной пирамидыТело, получающееся из
пирамиды, если отсечь
ее вершину плоскостью,
параллельной
основанию, называется
усеченной пирамидой.
D1
А1
С1
В1
D
А
С
В
4.
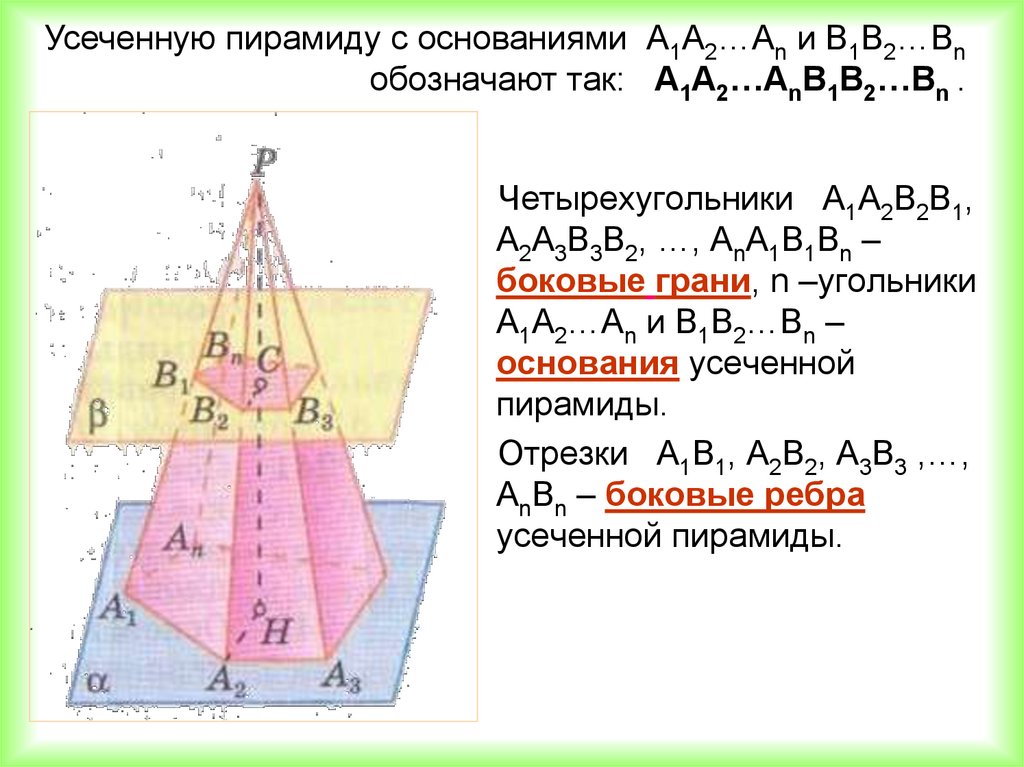
Усеченную пирамиду с основаниями А1А2…Аn и В1В2…Вnобозначают так: А1А2…АnВ1В2…Вn .
Четырехугольники A1A2B2B1,
A2A3B3B2, …, AnA1B1Bn –
боковые грани, n –угольники
А1А2…Аn и В1В2…Вn –
основания усеченной
пирамиды.
Отрезки А1В1, А2В2, А3В3 ,…,
АnВn – боковые ребра
усеченной пирамиды.
5.
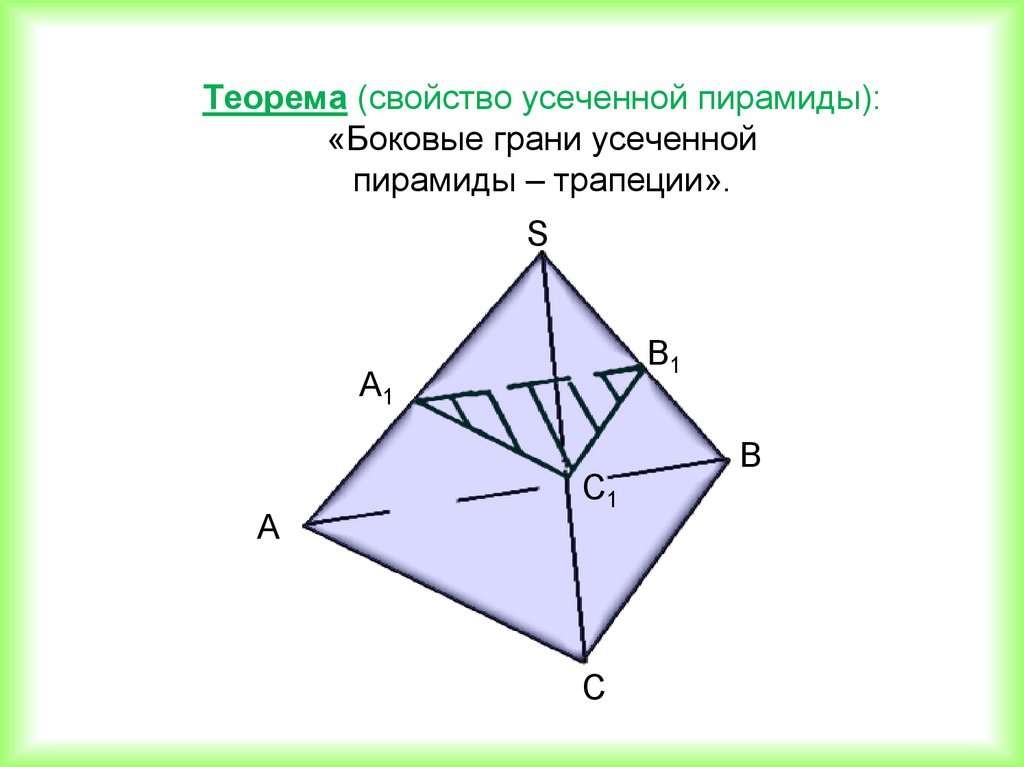
Теорема (свойство усеченной пирамиды):«Боковые грани усеченной
пирамиды – трапеции».
S
B1
А1
А
С1
С
B
6.
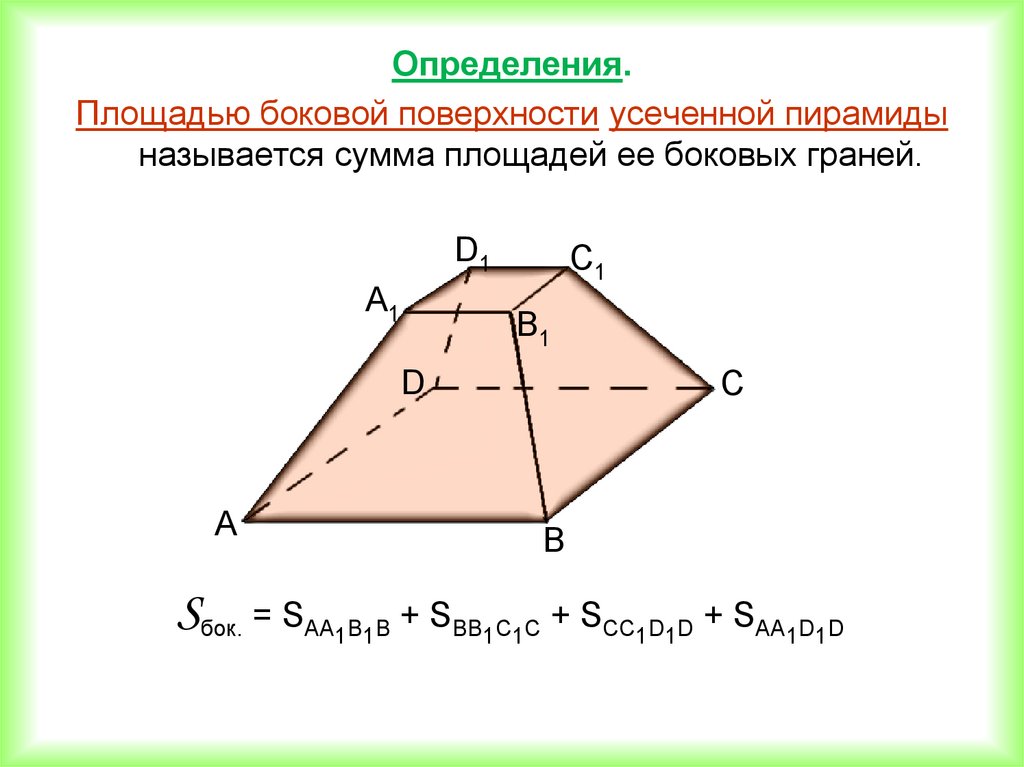
Определения.Площадью боковой поверхности усеченной пирамиды
называется сумма площадей ее боковых граней.
D1
А1
С1
В1
С
D
А
В
Sбок. = SАА1В1В + SВВ1С1С + SСС1D1D + SАА1D1D
7.
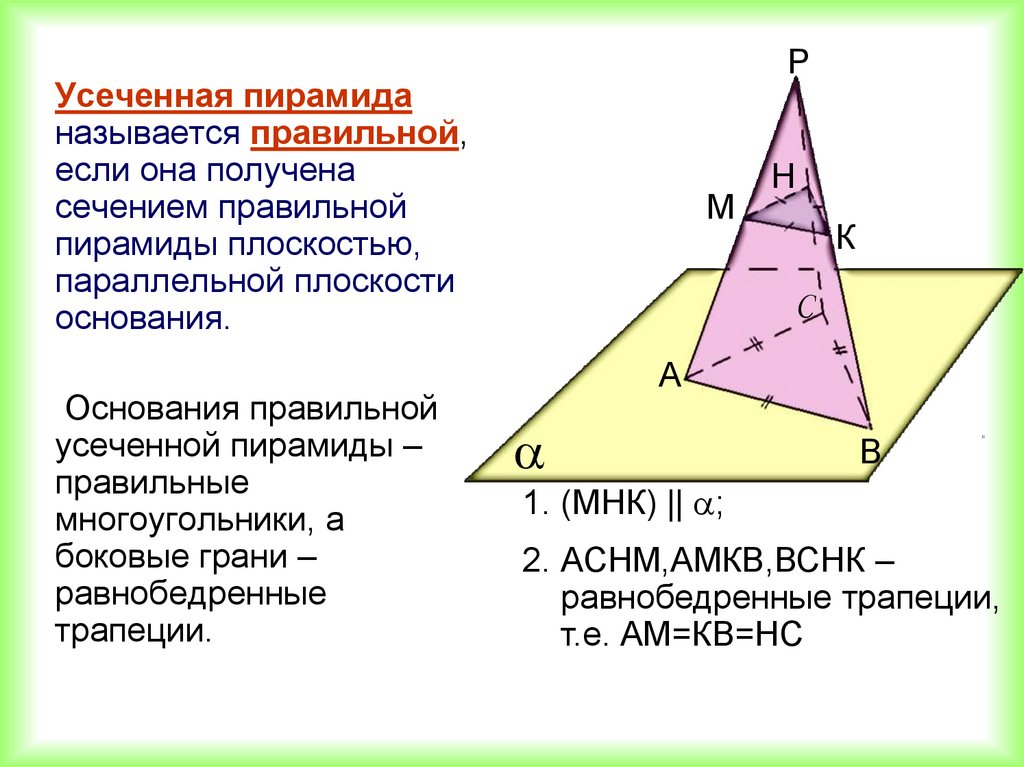
РУсеченная пирамида
называется правильной,
если она получена
сечением правильной
пирамиды плоскостью,
параллельной плоскости
основания.
Основания правильной
усеченной пирамиды –
правильные
многоугольники, а
боковые грани –
равнобедренные
трапеции.
М
Н
К
С
А
В
1. (МНК) || ;
2. АСНМ,АМКВ,ВСНК –
равнобедренные трапеции,
т.е. АМ=КВ=НС
8.
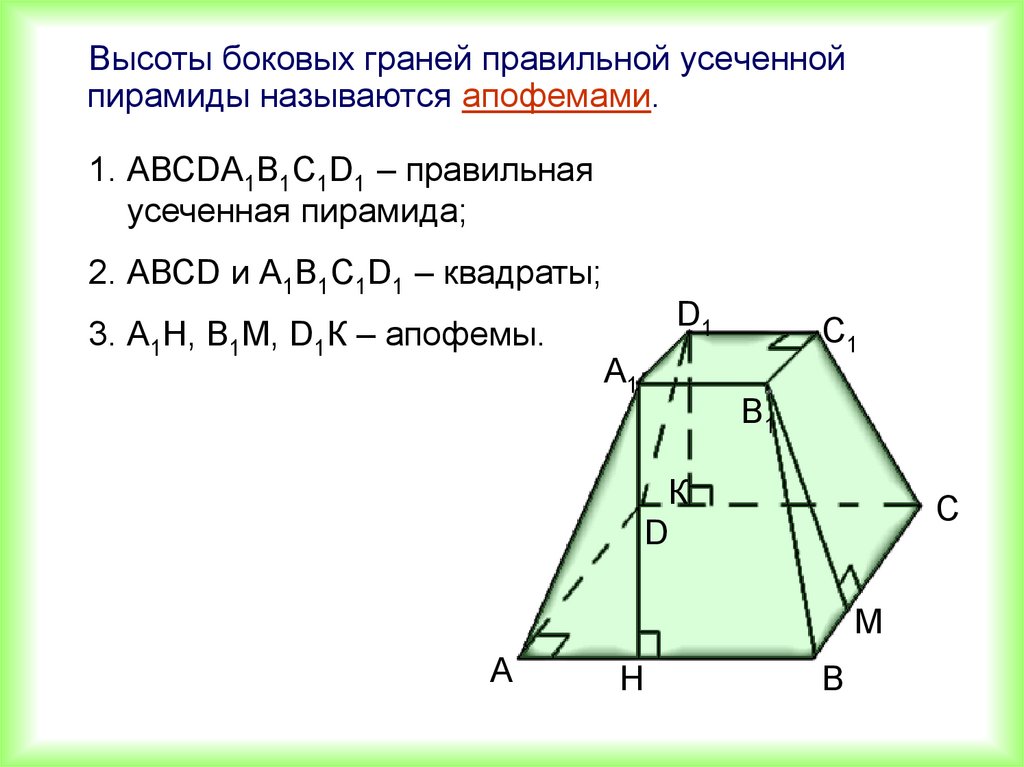
Высоты боковых граней правильной усеченнойпирамиды называются апофемами.
1. АВСDА1В1С1D1 – правильная
усеченная пирамида;
2. АВСD и А1В1С1D1 – квадраты;
3. А1Н, В1М, D1К – апофемы.
D1
А1
С1
В1
К
D
С
М
А
Н
В
9.
Теорема:Площадь боковой поверхности правильной усеченной
пирамиды равна произведению полусуммы периметров
оснований на апофему
1
Sб.п. Р1 Р2 ha
2
10. Отношение площадей оснований
S12
k
S2
где k - коэффициент подобия.
11.
Задачи1. Стороны
оснований
правильной
усеченной
треугольной пирамиды равны 6 см и 5 см. Апофема
равна 7 см. Найдите площадь полной поверхности
усеченной пирамиды.
2. В пирамиде проведено сечение параллельное
основанию через середину высоты. Площадь
основания равна 40 см2 . Чему равна площадь
сечения?
12.
Задачи3. Стороны оснований правильной треугольной
усеченной треугольной пирамиды равны 4 дм и 2
дм, а боковое ребро равно 2 дм. Найдите высоту и
апофему пирамиды.





 Математика
Математика








