Похожие презентации:
Основы теории пограничного слоя
1. ОСНОВЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
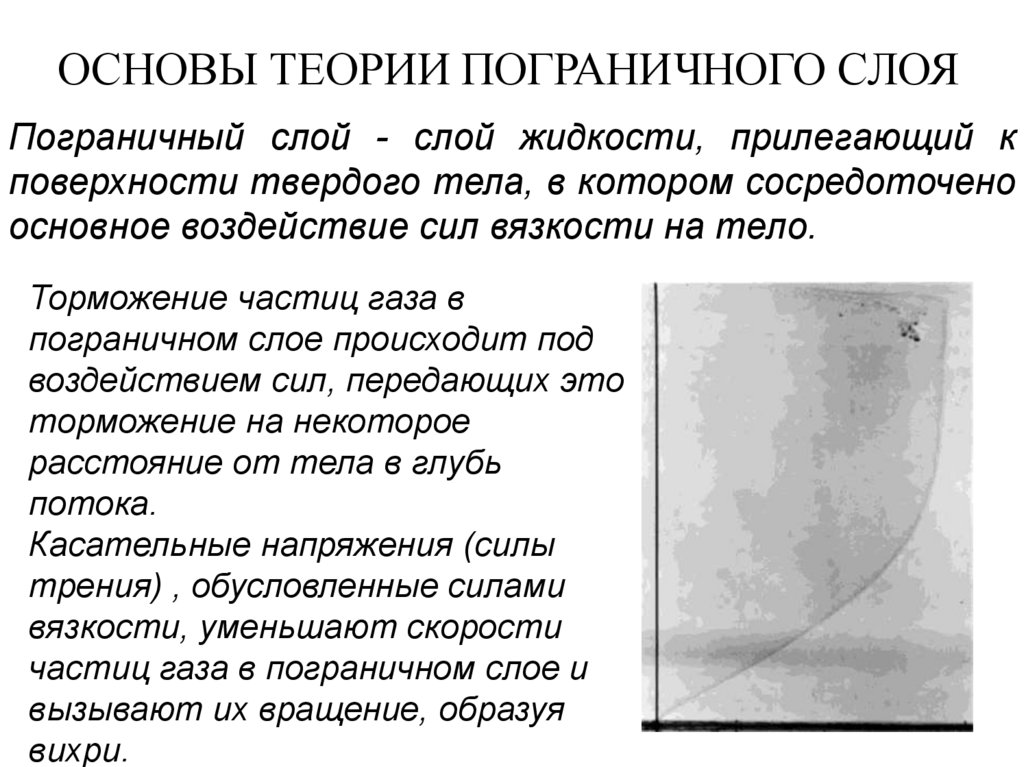
Пограничный слой - слой жидкости, прилегающий кповерхности твердого тела, в котором сосредоточено
основное воздействие сил вязкости на тело.
Торможение частиц газа в
пограничном слое происходит под
воздействием сил, передающих это
торможение на некоторое
расстояние от тела в глубь
потока.
Касательные напряжения (силы
трения) , обусловленные силами
вязкости, уменьшают скорости
частиц газа в пограничном слое и
вызывают их вращение, образуя
вихри.
2.
3.
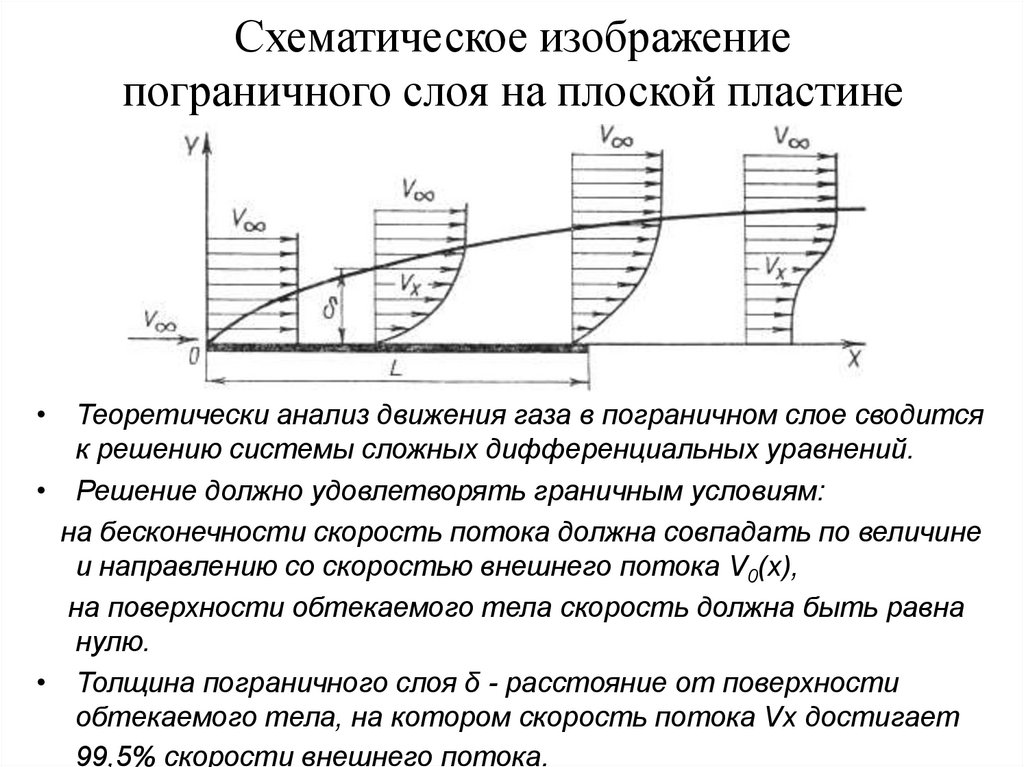
4. Схематическое изображение пограничного слоя на плоской пластине
• Теоретически анализ движения газа в пограничном слое сводитсяк решению системы сложных дифференциальных уравнений.
• Решение должно удовлетворять граничным условиям:
на бесконечности скорость потока должна совпадать по величине
и направлению со скоростью внешнего потока V0(x),
на поверхности обтекаемого тела скорость должна быть равна
нулю.
• Толщина пограничного слоя δ - расстояние от поверхности
обтекаемого тела, на котором скорость потока Vx достигает
99,5% скорости внешнего потока.
5.
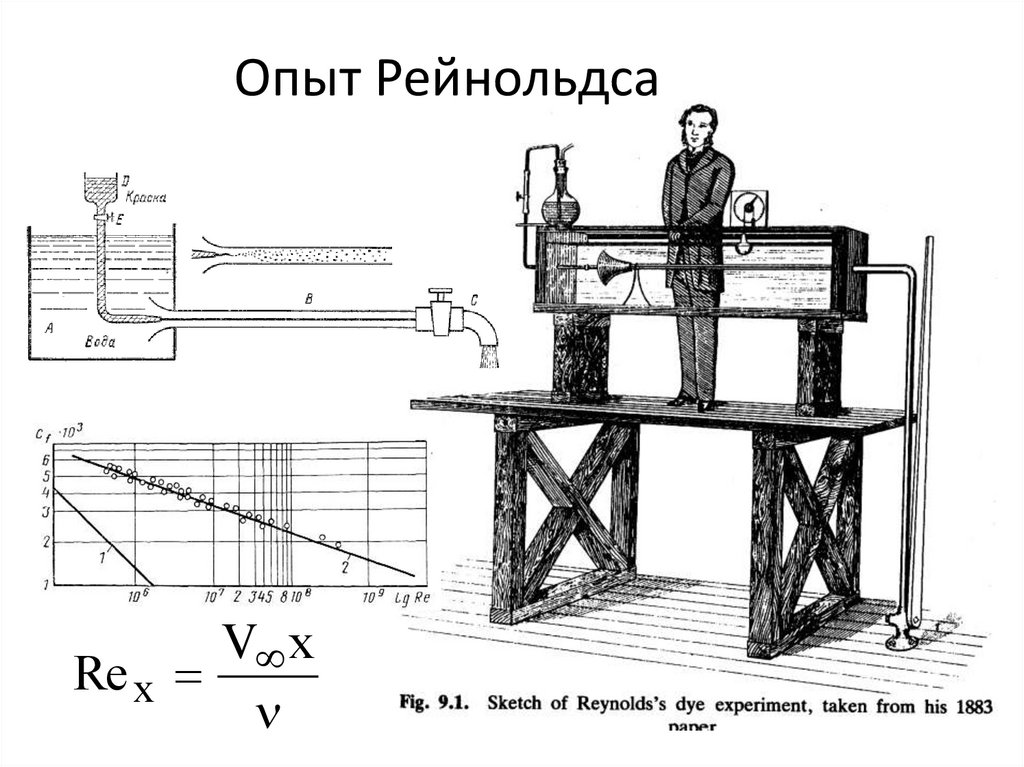
6. Опыт Рейнольдса
V xRe x
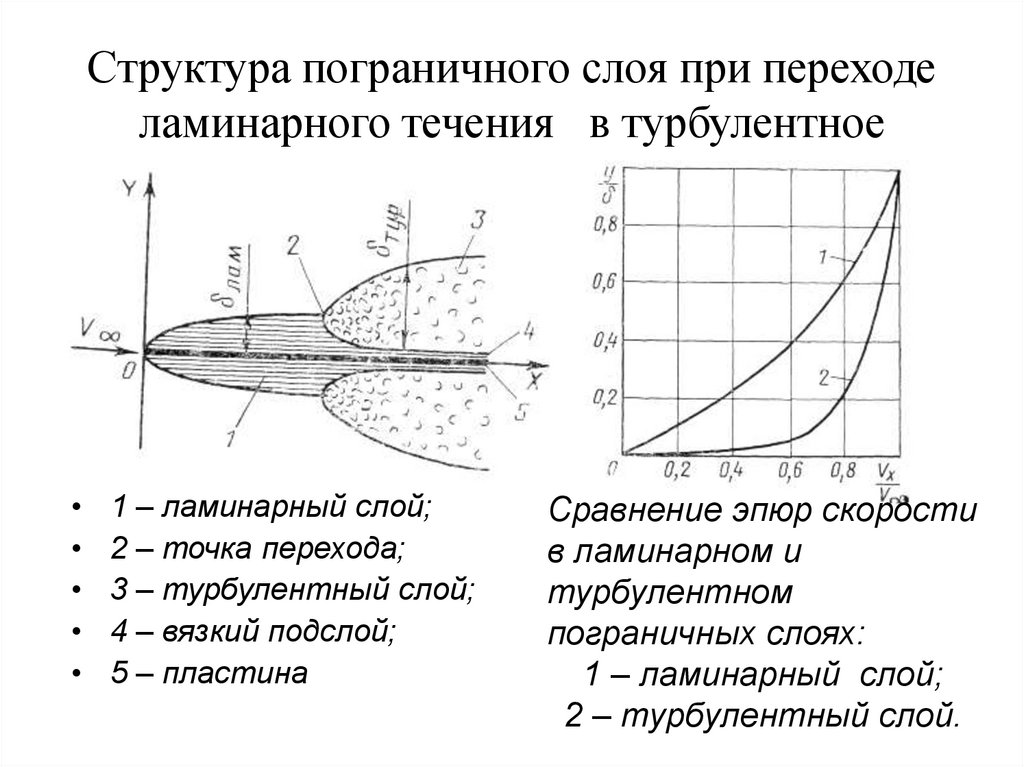
7. Структура пограничного слоя при переходе ламинарного течения в турбулентное
1 – ламинарный слой;
2 – точка перехода;
3 – турбулентный слой;
4 – вязкий подслой;
5 – пластина
Сравнение эпюр скорости
в ламинарном и
турбулентном
пограничных слоях:
1 – ламинарный слой;
2 – турбулентный слой.
8. Пример ламинарного и турбулентного ПС
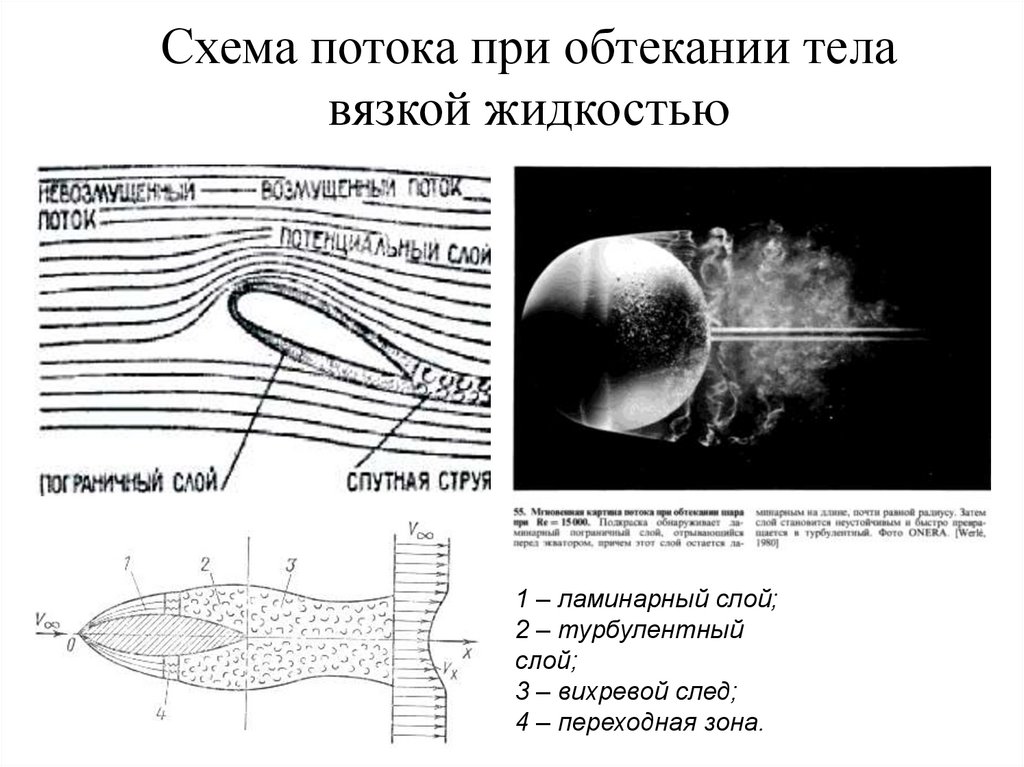
9. Схема потока при обтекании тела вязкой жидкостью
1 – ламинарный слой;2 – турбулентный
слой;
3 – вихревой след;
4 – переходная зона.
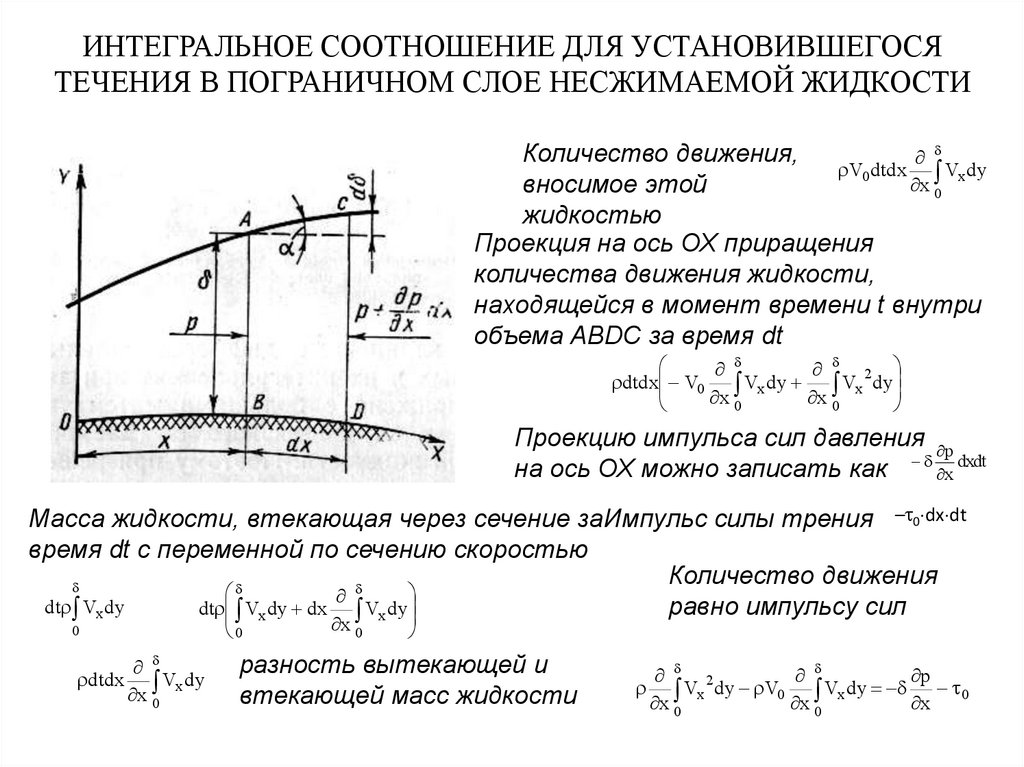
10. ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ДЛЯ УСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ В ПОГРАНИЧНОМ СЛОЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ
Количество движения,V0 dtdx Vx dy
x 0
вносимое этой
жидкостью
Проекция на ось ОХ приращения
количества движения жидкости,
находящейся в момент времени t внутри
объема ABDC за время dt
2
dtdx V0 Vx dy Vx dy
x 0
x 0
Проекцию импульса сил давления p
на ось ОХ можно записать как x dxdt
Масса жидкости, втекающая через сечение заИмпульс силы трения – 0 dx dt
время dt с переменной по сечению скоростью
Количество движения
dt Vx dy
равно импульсу сил
dt Vx dy dx Vx dy
x
0
dtdx Vx dy
x 0
0
0
разность вытекающей и
втекающей масс жидкости
2
p
V
dy
V
Vx dy 0
x
0
x 0
x 0
x
11. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО СООТНОШЕНИЯ ДЛЯ РАСЧЕТА ХАРАКТЕРИСТИК ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ ПЛОСКОЙ ПЛАСТИНЫ
Для плоской пластины интегральное соотношение несколькоупрощается.
На верхней границе V0 = V = const из уравнения Бернулли dp/dx=0
d 2
d
интегральное соотношение принимает вид dx Vx dy V0 dx Vx dy 0
0
0
Приближенно закон распределения
скорости по поперечному сечению
Vх = а + bу + су2
Для пластины граничные условия будут следующими:
а) на нижней границе пограничного слоя (у стенки) при у = 0 Vx = 0
б) на верхней границе пограничного слоя (в потоке) при у = δ Vx = V∞
в) на верхней границе пограничного слоя отсутствуют силы трения (τ = 0),
Из этих граничных условий находимa = 0, b 2 V
значения коэффициентов:
закон распределения скоростей по
поперечному сечению пограничного слоя
запишем в виде
V
c
2
y
Vx V 2
y 2
2
12. Вводя число Рейнольдса
формула Ньютона дляV
V
y 2
2
определения напряжения трения 0 2
Vx dy
2y
dy V
3
0
0
на стенке
Определяя значения интегралов:
2
V 2
y 2
8
2
Vx dy
2y
dy V 2
0
15
0
при этих подстановках 2 V 2 d 2 V
15
dx
уравнение
1 2
преобразуется:
15
x C
Интегрируя это уравнение, получим:
V
2
Толщина пограничного
слоя
5.48
x
V
Подставив полученное значение δ
найдем:
Изменение напряжения
трения и толщины
пограничного слоя по
длине пластины
V x
Вводя число Рейнольдса Re x
V 3
0 0.365
x
5.48
x
Re x
Точное решение задачи о
пограничном слое,
полученное Блазиусом в
x
5.48
результате
Re x
интегрирования
дифференциальных
V 3
0.332
уравнений движения вязкой 0
x
жидкости, дает точный
ответ:
13. РАСЧЕТ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО СЛОЯ СОПРОТИВЛЕНИЕ ПЛОСКОЙ ПЛАСТИНЫ
1y n
экспериментально установлено, что в турбулентном
пограничном слое распределение скоростей приближенно
может быть представлено в виде степенного закона:
Vx
V
1
y 7
Vx
V
Для скоростей невозмущенного потока, не
превышающих половины скорости звука
1
1 4
0 0.0225 V 2
Re
экспериментальная зависимость для
напряжения трения τ0 на пластине
при турбулентном режиме течения:
По аналогии с ламинарным вычислим значения двух
интегралов и подставив в интегральное соотношение
после преобразований и
разделения переменных
касательное
1
4
d 0.0225
1
4
72
dx
7 V
1
5
напряжение 0 0.0289 V 2
V
При изменении чисел Рейнольдса в
диапазоне 10 6 < Re < 10 9 хорошее
согласование с опытом дает
формула
Cf
1
5
x
0.458
(lg Re)1.58
0
7
d
V 2
72
dx
толщина пограничного слоя
турбулентный
= 0,37 x (1/Reх)1/5
Cf
0.072
Re0.2
ламинарный
5.48
x
Re x
Cf = 1,328/Re
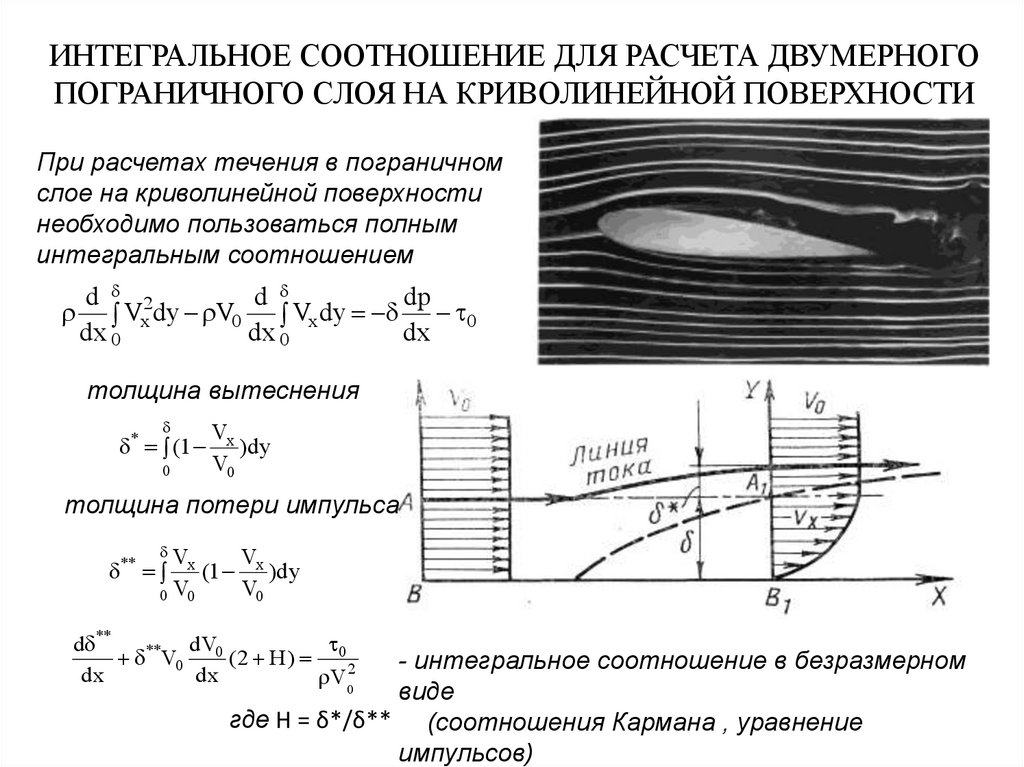
14. ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ДЛЯ РАСЧЕТА ДВУМЕРНОГО ПОГРАНИЧНОГО СЛОЯ НА КРИВОЛИНЕЙНОЙ ПОВЕРХНОСТИ
При расчетах течения в пограничномслое на криволинейной поверхности
необходимо пользоваться полным
интегральным соотношением
d 2
d
dp
Vx dy V0
V
dy
0
x
dx 0
dx 0
dx
толщина вытеснения
* (1
0
Vx
)dy
V0
толщина потери импульса
**
V
x
0
V0
(1
Vx
)dy
V0
d **
dV
**V0 0 ( 2 H ) 0 2
dx
dx
V
- интегральное соотношение в безразмерном
0
виде
где Н = δ*/δ** (соотношения Кармана , уравнение
импульсов)
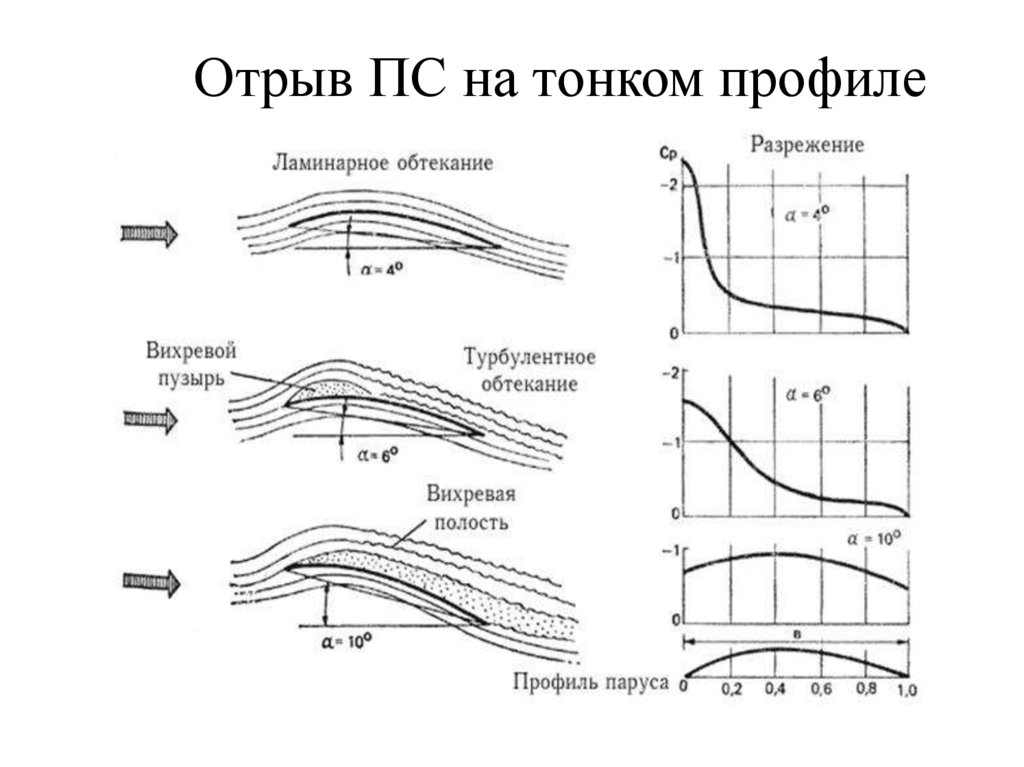
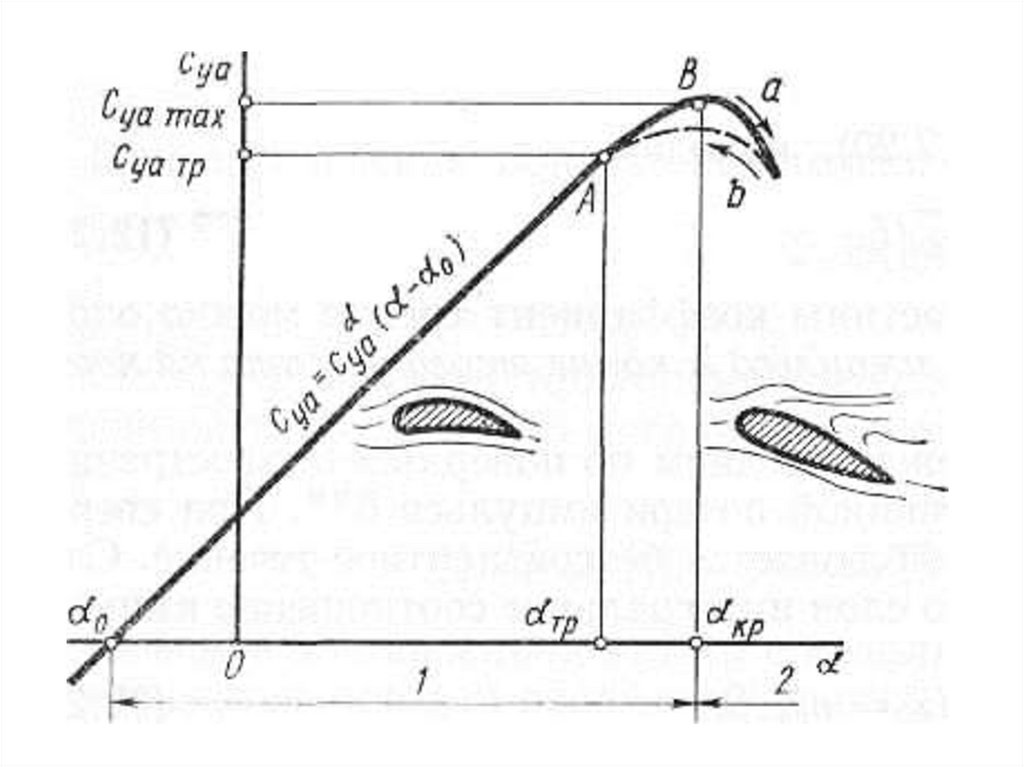
15. ОТРЫВ ТЕЧЕНИЯ В ПОГРАНИЧНОМ СЛОЕ
Точкой отрыва пограничного слояназывается точка, в которой
производная скорости равна 0:
На стенке напряжение трения
0
Vx
y
Vx
y
0
y 0
0
y 0
В точке отрыва поток начинает отходить от стенки под небольшим углом. За
точкой отрыва под действием положительного градиента давления возникает
возвратное течение
16. Отрыв ПС на тонком профиле
17.
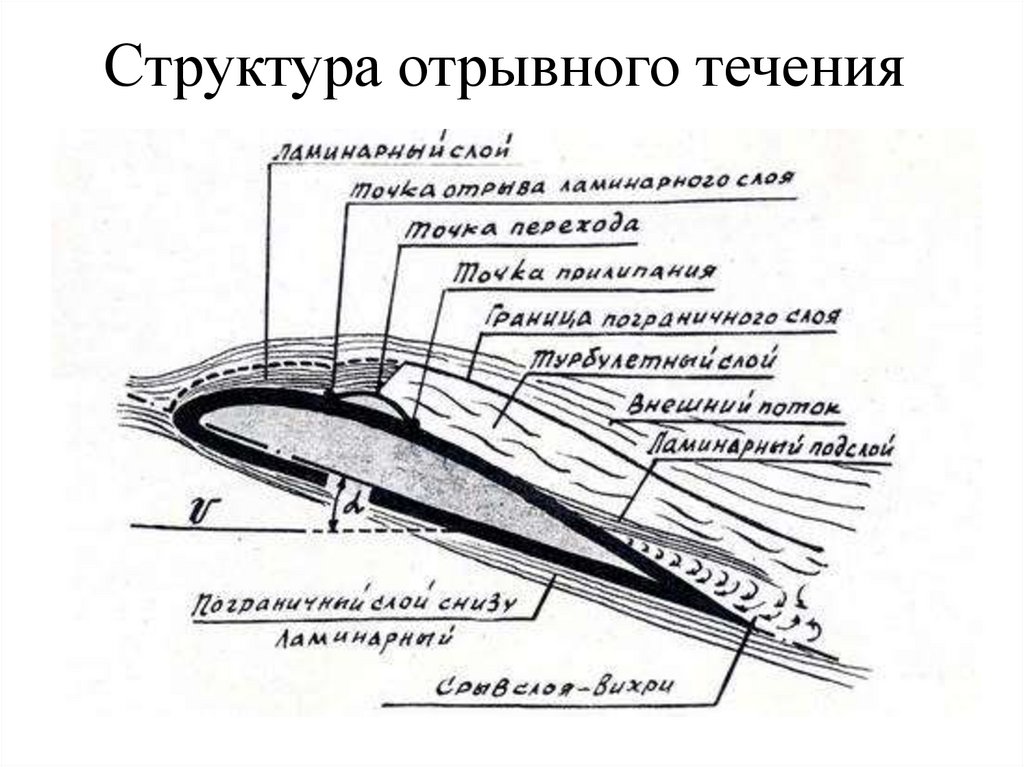
18. Структура отрывного течения
19. Влияние чсила Re на отрыв ПС
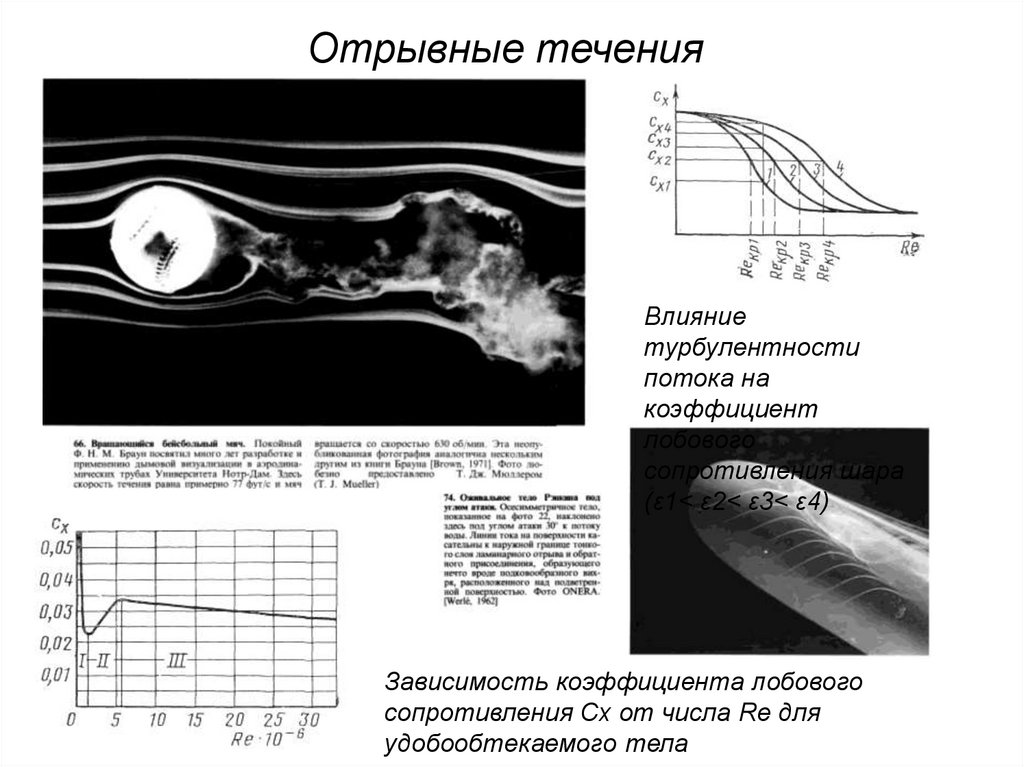
20. Отрывные течения
Влияниетурбулентности
потока на
коэффициент
лобового
сопротивления шара
(ε1< ε2< ε3< ε4)
Зависимость коэффициента лобового
сопротивления Сх от числа Re для
удобообтекаемого тела
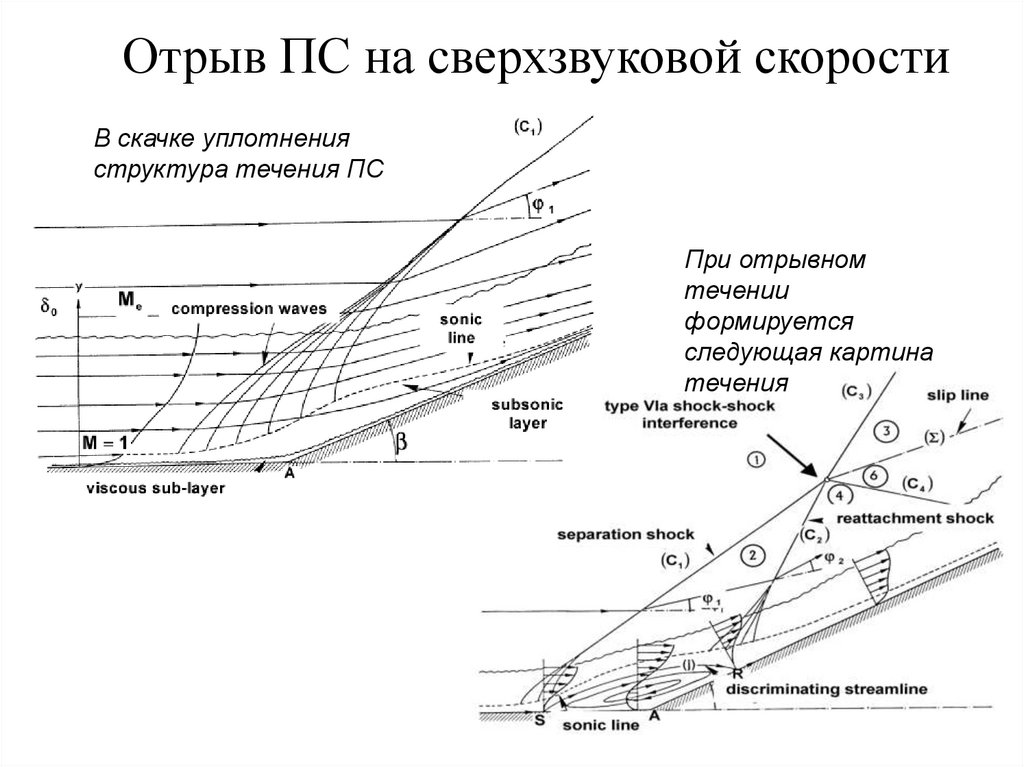
21. Отрыв ПС на сверхзвуковой скорости
В скачке уплотненияструктура течения ПС
При отрывном
течении
формируется
следующая картина
течения
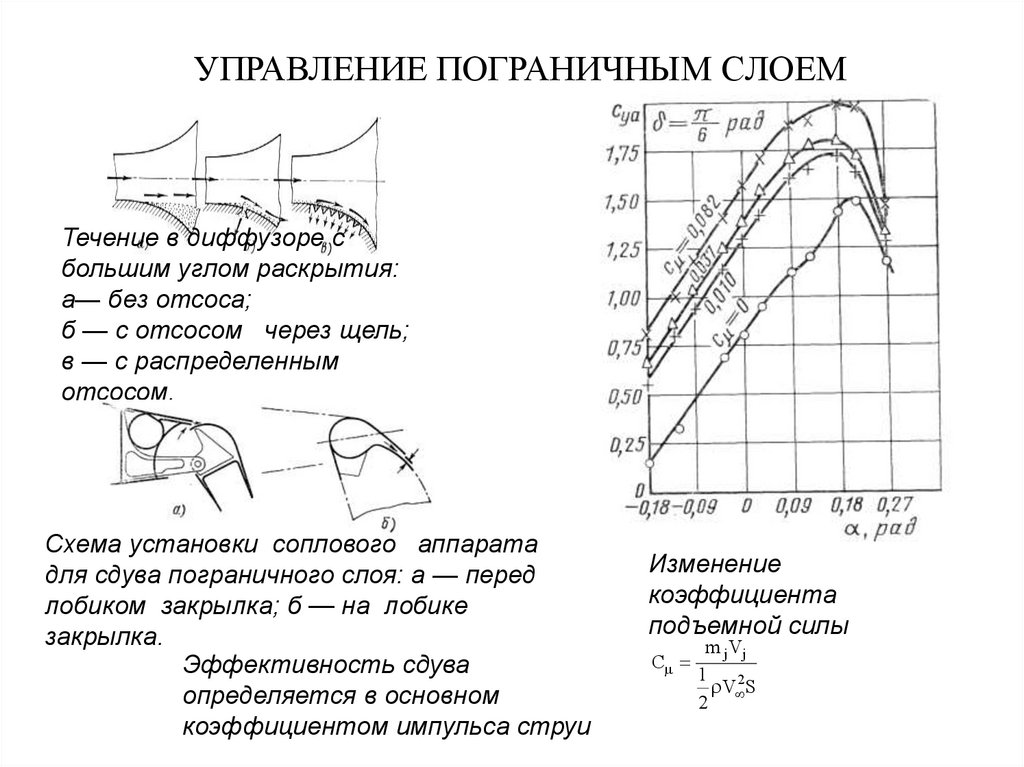
22. УПРАВЛЕНИЕ ПОГРАНИЧНЫМ СЛОЕМ
Течение в диффузоре сбольшим углом раскрытия:
а— без отсоса;
б — с отсосом через щель;
в — с распределенным
отсосом.
Схема установки соплового аппарата
для сдува пограничного слоя: а — перед
лобиком закрылка; б — на лобике
закрылка.
Эффективность сдува
определяется в основном
коэффициентом импульса струи
Изменение
коэффициента
подъемной силы
C
m j Vj
1 2
V S
2









 Физика
Физика








