Похожие презентации:
Аэрогазодинамика. Пограничный слой. Аэродинамический нагрев (лекции 14, 15)
1. Пограничный слой. Аэродинамический нагрев
АэрогазодинамикаПограничный слой.
Аэродинамический нагрев
Лекции 14, 15
2.
Сопротивление удобообтекаемых тел при их движениив жидкостях или газах является в значительной
степени сопротивлением от трения среды о
поверхность тела. Поэтому весьма важно знать законы
трения в жидкостях и газах и уметь рассчитывать
сопротивление трения.
Силы трения жидкости проявляются не во всей среде,
а лишь в слое, прилегающем к поверхности движущегося тела, где скорость течения
резко изменяется по нормали к
поверхности, и в следе
за телом
2
3.
Задача об обтекании тела потоком вязкой жидкостирешается интегрированием дифференциальных
уравнений движения с учетом внутреннего трения –
уравнений Навье-Стокса.
В общем случае, когда коэффициент вязкости
зависит от температуры, уравнения движения в
проекции на оси пространственной декартовой
системы координат имеют вид
Vx
p Vx 2
Vx Vy Vx Vz
X 2 divV ,
t
x x x 3
y y x z z x
Vy
Vy Vz Vy Vx
p Vy 2
Y 2 divV ,
t
y y y 3
z z y x x y
Vz
Vz 2
Vz Vx Vz Vy
Z 2 divV .
t
z z z 3
x x z y y z
3
4.
При const уравнения Навье-Стокса имеют видdVx
1 p
X
divV Vx
dt
x 3 x
и т.д.
Точное решение задачи обтекания какого-либо тела
сводится к интегрированию дифференциальных
уравнений при заданных граничных условиях и
практически невозможно. Для получения частных
решений какого-либо определенного класса задач
прибегают к упрощению этих уравнений.
При изучении обтекания тел при больших числах
Рейнольдса, характерных для авиационной и
ракетной техники, применяют метод упрощения
уравнений Навье–Стокса, основанный на понятии
пограничного слоя
4
5. 14.1.Толщина пограничного слоя
Течение жидкости в пограничном слое может бытьламинарным или турбулентным. При ламинарном
течении наблюдается упорядоченное движение
жидкости параллельными слоями (слоистое течение)
без их перемешивания. Турбулентное течение
сопровождается беспорядочным движением частиц
(не молекул) жидкости, приводящим к поперечному
перемешиванию вязкой среды и к пульсации
параметров течения.
Формула Ньютона для силы внутреннего трения при
V
ламинарном течении
показывает, что внутри
n
пограничного слоя и в следе за телом, где градиенты
скорости значительны, силой внутреннего трения
пренебрегать нельзя, и среду, движущуюся внутри
этих областей, следует считать вязкой даже при
малых значениях коэффициента вязкости.
5
6.
Во внешнем потоке вне пограничного слоя скоростьпри удалении от поверхности тела изменяется
чрезвычайно медленно. Влияние вязкости здесь
пренебрежимо мало, и можно считать, что движение
подчиняется законам течения идеальной невязкой
жидкости. Изучать движение среды в этой области
можно с помощью уравнений Эйлера.
Толщина пограничного слоя величина достаточно
условная.
Обычно за толщину пограничного слоя в данной
точке поверхности принимают расстояние от тела до
такой точки, в которой действительная скорость
потока отличается от скорости в потенциальном
Vx
течении на 1 %:
0,99
U y
6
7. 14.2. Толщина вытеснения
Секундные расходы жидкости через сечениепограничного слоя высотой для потоков невязкого и
вязкого газов различны:
невязкий
вязкий
Vx
Udy
V
dy
U
V
dy
U
x
0
0 x 0
0 1 U dy
Толщина вытеснения характеризует
Схема к определению
уменьшение секундного расхода газа
толщины вытеснения
при =const
через сечение пограничного слоя
вследствие торможения потока в пограничном слое
V
V
U U 1 x x dy
dy
U
U
0
V
1 x dy
U
0
сжимаемая жидкость
несжимаемая жидкость
*
*
*
7
8.
Толщина вытеснения характеризует искривление линийтока вследствие торможения потока в пограничном
слое.
Известно, что расход жидкости
в трубке тока одинаков во всех
сечениях. Отсюда
y
U AB Vx dy ( y BC ) U
0
ВС– смещение линии тока
Vx
*
BC 1
dy
вязкого потока по отношению
U
0
к линии тока невязкого потока.
Т.е. толщина вытеснения – это толщина, на которую
отодвигаются от тела линии тока в вязком газе по
отношению к линиям тока в невязком газе.
8
9. 14.3.Толщина потери импульса
Вследствие торможения потока в пограничном слоепроисходит не только уменьшение расхода по
сравнению с невязким газом, но и уменьшение
количества движения, проносимого жидкостью
через
сечение пограничного слоя, равное Vx (U Vx )dy .
Толщина потери импульса **– условная толщина
некоторого слоя, сквозь сечение которого в единицу
времени с постоянной скоростью переносится
количество движения, равное
2 **
указанному уменьшению импульса U Vx U Vx dy
0
Vx Vx
1 dy
U U
0
**
сжимаемая жидкость
Vx Vx
1 dy
U U
0
**
несжимаемая жидкость
0
* **
9
10. 14.4.Дифференциальные уравнения пограничного слоя в несжимаемой жидкости
Для области тонкого пограничногослоя, в котором собственно и проявляются силы трения, Л.Прандтль
предложил метод упрощения уравнений движения, основанный на
сравнении порядка величины членов уравнения и
отбрасывания членов высшего порядка малости.
2Vx 2Vx
Vx
Vx
1 p
Vx
Vy
2 2
x
y
x
y
x
2Vy 2Vy
1 p
Vx
Vy
2 2
x
x
y
x
y
Vy
Vy
Уравнения Навье-Стокса
Vx Vy
0
x
y
Уравнение неразрывности
10
11.
Эта система уравнений полностью описывает движениевязкой жидкости в пределах пограничного слоя в рамках
настоящей задачи.
Оценим порядок входящих в эти уравнения членов,
имея в виду, что 0 y , т. е. y имеет порядок толщины
пограничного слоя (y ) и является малой величиной
по сравнению с характерным размером обтекаемой
поверхности, например, его длиной l ( / l 0). Скорость
в пределах пограничного слоя 0 Vx V ( Vx V ), продольная координата 0 x l , т. е. x l.
Тогда приращение скорости Vx Vx имеет порядок
величины скорости во внешнем потоке V .
Установив порядок производных входящих в первое из
уравнений Навье-Стокса, произведя упрощения получим
11
12.
VxVx
1 p
2Vx
Vx
Vy
2
x
y
x
y
Внутри пограничного слоя силы вязкости и инерции
имеют одинаковый порядок, т. е. их отношение должно
быть равным единице. V 2 V
: 2 1, следовательно
Их отношение равно
l
V 2 2 Vl 2
Re
1,
l V l 2
l
2
~
l
1
Re
Проведя подобный анализ членов второго уравнения,
приходим к аналогичной упрощенной записи
Vy
Vy
2Vy
1 p
Vx
Vy
2
x
y
y
y
Инерционные и вязкие члены этого уравнения относят-
ся к соответствующим членам первого уравнения как
/ l 0. Очевидно, что в данной задаче вклад второго
уравнения не превышает указанного отношения.
12
13.
Поэтому инерционными и вязкими членами второгоуравнения можно пренебречь и в задаче исследования
течения в пограничном слое вообще не учитывать.
Тогда из второго уравнения системы с достаточной
p
точностью можно записать следующее
0
y
давление внутри пограничного слоя
не меняется вдоль нормали к контуру тела и равно
давлению на внешней границе пограничного слоя
dp
p
p
0
Так как
, то p p( x) и
=
. Система диффеdx
x
y
ренциальных уравнений
Vx
Vx
1 dp
2Vx
Vx
Vy
2 ,
для пограничного слоя
x
y
dx
y
примет вид
V V
x
x
y
y
0.
13
14. 14.5.Интегральное соотношение пограничного слоя
Рассмотрим установившийся плоскийпограничный слой. Выделим в пограничном слое малый объем АВСD.
Применим к данному объему теорему
об изменении количества движения. Вычислим изменение количества движения в направлении оси ОХ за
промежуток времени dt.
d 2
d
Vx dy U Vx dy dxdt
dx 0
dx 0
Приравняем его суммарному импульсу от сил давления
и трения, действующих на грани выделенного объема.
d p
dx
От сил давления: p , pd и p
dx
14
15.
dpdxdt
Суммарный импульс сил давления
dx
Импульс от силы трения 0 dx 1 dt.
Изменение количества движения жидкости в объеме
= суммарному импульсу от сил давления и трения
d
d
dp
2
Получаем
V
dy
U
V
dy
0
x
x
dx 0
dx 0
dx
интегральное соотношение пограничного слоя
Пригодно для изучения ламинарного и турбулентного
пограничных слоев, но необходимы два дополнительных уравнения:
1. Закон распределения скорости по поперечному
сечению пограничного слоя (можно задать
приближенно аппроксимирующей функцией).
2. Зависимость напряжения трения от изменения
скорости по нормали к поверхности (например,
формула Ньютона для ламинарного п.с.)
15
16. 15.1. Расчет пограничного слоя на плоской поверхности в несжимаемой среде
Задача расчета пограничного слоя в несжимаемойсреде сводится к определению закона изменения
толщины пограничного слоя, т. е. x , и силы
сопротивления трения X тр при условии, что известны
скорость V , величина коэффициента кинематической
вязкости и хорда пластинки b.
Для плоской пластинки скорость потенциального течения U V , градиdp
0
ент давления вдоль пластинки
dx
Тогда интегральное соотношение
примет вид
d
d
2
dx 0
Vx dy V
dx 0
Vx dy 0
16
17. 15.2.Ламинарный пограничный слой
Закон распределения скорости по толщине ПС2
Vx
y y
y
a b c d
V
3
Коэффициенты полинома - из граничных условий:
Кинематические: Vx y 0 0 и Vx y V
2Vx
2Vx
1 dp
dp
0, То 2 0
Динамические: 1) 2
, т.к.
dx
y y 0 dx
y y
Vx
2) при y
y
0 и
Vx
y 0
y
Тогда из закона распределения скорости получаем:
3
1
a с 0, b , d . Т.е.
2
2
Vx 1 y y 3
3 3
V 2
17
18.
Выражение для 0 получим из закона Ньютона длявнутреннего трения при ламинарном течении. Т.к.
3 V
Vx 3 V
y2
,то
1
0
2
y
2
2
Интегралы, входящие в интегральное соотношение
V y y 3
5
V
dy
3
dy
V
0 x
2 0 3
8
2
V y y 3
17
2
2
V
dy
3
dy
V
.
3
0 x
4 0
35
Теперь интегральное соотношение преобразуется в
обыкновенное дифференциальное уравнение
17
d 5 2 d
3 V
V 2
V
35
dx 8
dx
2
Группируя подобные члены и разделяя переменные
интегрируем
13
2
280
V x C
18
19.
Из условий на передней кромке х = = 0 и С = 0;после преобразований
4,64 x
280 x
x
13 V
4,64
V
0
Местный коэффициент трения c f
V 2 2
Re x
0,65
cf
Re x
Коэффициента сопротивления трения
b
1,3
1
cx тр
cx тр c f dx
Re
b0
В качестве характерного линейного размера в числе
Рейнольдса используется хорда пластинки b
19
20. 15.3.Турбулентный пограничный слой
Ламинарное течение в пограничном слое плоскойпластины возможно лишь в случае, если число
Рейнольдса не превышает некоторого значения,
называемого критическим.
Для числа Рейнольдса, в котором за характерную
длину принято расстояние x от входной кромки
пластины, критическое число Re x = 9 104...1,1 106.
При превышении критического
числа Рейнольдса происходит
турбулизация течения.
Законы турбулентного течения
наиболее полно изучены для
движения жидкости в круглых трубах
20
21.
Допустим, что в пограничном слое профиль Vx y 1 7V
скорости такой же, как и в круглой трубе
14
Воспользуемся зависимостью
2
0,225
V
касательных напряжений на стенке, 0
V
полученной для труб
Интегралы, входящие в интегральное соотношение
7
V
dy
0 x 8 V
7
2
V
dy
V 2
0 x
9
14
7
2 d
2
V
0,225
V
Интегральное соотношение
12
dx
V
Толщина турбулентного пограничного слоя
Местный коэффициент трения
cf
0,057 8
5 Re
x
Коэффициент сопротивления трения (/)
0,37 x
5 Re
x
0,072
cx тр 5
Re
21
22.
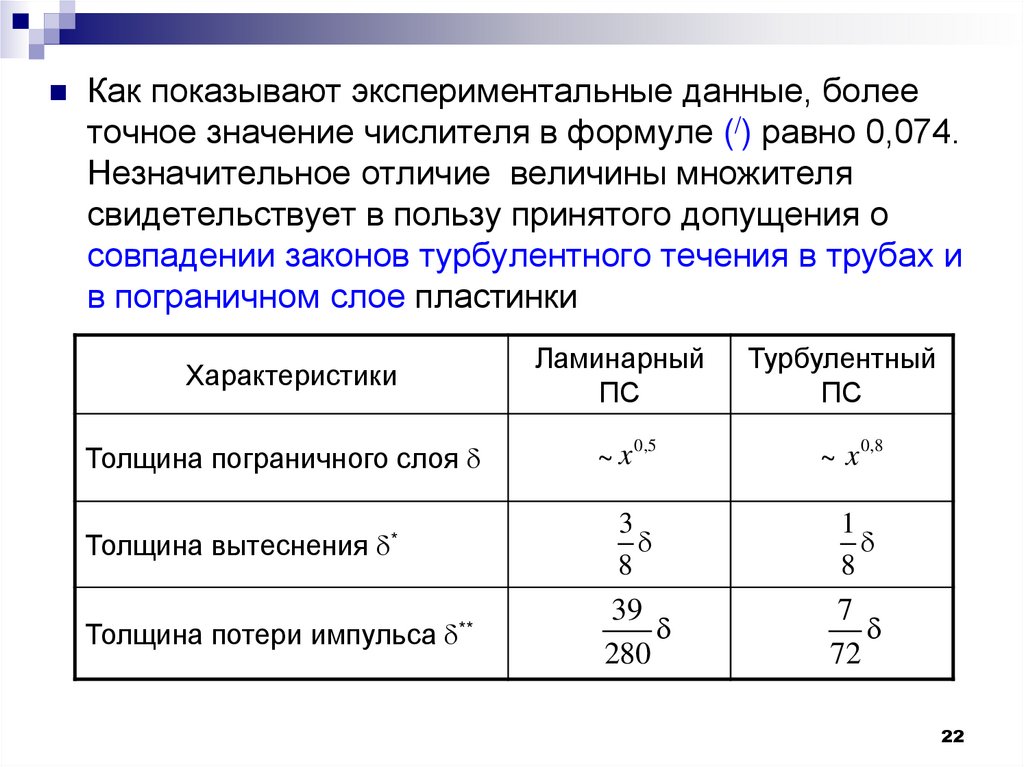
Как показывают экспериментальные данные, болееточное значение числителя в формуле (/) равно 0,074.
Незначительное отличие величины множителя
свидетельствует в пользу принятого допущения о
совпадении законов турбулентного течения в трубах и
в пограничном слое пластинки
Характеристики
Ламинарный
ПС
Толщина пограничного слоя
~x
0,5
Турбулентный
ПС
~x
0,8
Толщина вытеснения *
3
8
1
8
Толщина потери импульса **
39
280
7
72
22





















 Физика
Физика








