Похожие презентации:
Характеристические уравнения реакторов
1. Характеристические уравнения реакторов
2.
Одной из важнейших задач, возникающих при изучении процессов, протекающих в реакторах, являетсяустановление функциональной зависимости времени
пребывания реагентов в реакторе от различных
факторов. Данную зависимость выражают в виде
уравнения, которое называют характеристическим
уравнением реактора:
τ = f(x,C0,r).
Характеристическое уравнение составляется на основании материального баланса по одному из
компонентов реакционной смеси, например,
уравнение
3.
4.
Первый член уравнения ,характеризует общее изменениеконцентрации исходного реагента во времени (это скорость
процесса, не реакции!). Выражение после знака равно - сумма произведений составляющих скорости потока вдоль осей
координат на градиенты концентраций. По сути данное
выражение отражает изменение концентрации реагента А
вследствие его переноса реакционной массой в направлении, совпадающем с направлением всего потока.
Второе слагаемое в правой части это произведение коэффициента диффузии на сумму вторых производных от концентрации по осям координат - отражает изменение концентрации реагента в элементарном объеме в результате
его переноса за счет диффузии.
Последний член уравнения - скорость химической реакции,
показывает изменение концентрации исходного вещества А
в элементарном объеме за счет химической реакции .
5.
Следует отметить, что указанное уравнение неучитывает характер теплового режима реактора и
влияние температуры на кинетику химической
реакции, поэтому для выбора оптимального режима
работы реактора уравнение материального баланса
решается совместно с уравнением теплового баланса.
Рассмотрим характеристические уравнения реакторов
различных типов на примере простой необратимой
реакции А —► R. Для более сложных химических
превращений уравнения составляются аналогичным
образом с учетом вида кинетического уравнения в
каждом конкретном случае.
6.
В реакторе идеального вытеснения (РИВ) реакционная смесь движется только в одномнаправлении - по длине реактора. Выберем
направление движения потока реагентов за
направление оси х. Тогда можно записать
следующие выражения:
7.
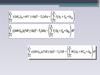
В РИВ отсутствует продольная и радиальнаядиффузия, поэтому сумма вторых производных
концентрации А по координатам равна нулю.
Тогда уравнение примет вид:
8.
9.
После преобразования для кинетического уравнения видаПолучим
где ХА-степень превращения вещества.
Итак, имея концентрацию исходного вещества
константу реакции и задавшись степенью
превращения можно получить расчетное время
нахождения реакционной смеси в реакторе.
10.
Можно показать, что реактор идеального смешенияпериодического действия описывается
тем же уравнением.
Характеристическое уравнение РИС-Н
При стационарном режиме работы реактора
идеально-го смешения непрерывного действия (РИС-Н)
скорость химического превращения реагента А равна
скорости его конвективного переноса:
где v - объемный расход реакционной смеси,
V - объем реакционной смеси,
САо - концентрация реагента А на входе в реактор.
11.
После преобразования для кинетического уравнениявида
получим
12.
Используя полученные уравнения можносравнить эффективность реакторов . Очевидно,
что РИВ выгоднее РИС.













 Химия
Химия