Похожие презентации:
Подготовка к комплексному экзамену
1. Подготовка к комплексному экзамену
12. 1. Правило Крамера
Рассмотрим СЛУ с тремя неизвестными:a11 x a12 y a13 z b1
a21 x a22 y a23 z b2
a x a y a z b
32
33
3
31
a11
a12
a13
a 21
a 22
a 23
a 31
a 32
a 33
Из
коэффициентов
системы составим
определитель:
Случай, когда ∆≠0.
Определитель называют
определителем системы.
2
3.
Т.к.0,
y
x
z
x , y , z
Формулы получили название формул
Крамера и применимы лишь в случае, если
определитель системы отличен от нуля.
3
4.
a11 x a12 y a13 z b1a21 x a22 y a23 z b2
a x a y a z b
32
33
3
31
a11
a12
a13
a 21
a 22
a 23
a 31
a 32
a 33
b1
a12
a13
x b2
a22
a23
b3
a32
a33
a11
b1
a13
y a21 b2
a23
a31 b3
a33
a11
a12
b1
z a21 a22
b2
a31
b3
a32
4
5.
56. 2. Матричный способ решения СЛУ (с помощью обратной матрицы)
Рассмотрим систему трёх линейных уравнений с тремянеизвестными:
a11x1 a12 x2 a13 x3 b1
a21x1 a22 x2 a23 x3 b2
a x a x a x b
31 1 32 2 33 3 3
В матричной форме записи эта система уравнений имеет вид
A X B
a11 a12 a13
A a21 a22 a23 ;
a
31 a32 a33
x1
b1
X x2 ; B b2 .
x
b
3
3
7. 2. Матричный способ решения СЛУ (с помощью обратной матрицы)
A X BA X B A
1
1
A 0
1
A A X A B
1
X A B
8.
89.
910.
1011.
Экстремумы функции двух переменных.Пусть функция z=f(x,y) определена в
некоторой окрестности М0(x0,y0).
Функция z=f(x,y) имеет в точке М0(x0,y0)
локальный максимум (минимум), если
существует окрестность в точке М0, в
которой для любой точки М(x,y):
f ( x, y) f ( x0 , y0 ) [ f ( x, y) f ( x0 , y0 )]
Это точки экстремума.
12.
Необходимое условие экстремума:Если функция f(x,y) в точке М0(x0,y0)
имеет экстремум и частные
производные первого порядка, то в
этой точке:
f ( x0 , y0 ) f ( x0 , y0 ) 0
/
x
/
y
13.
Достаточное условие экстремума:Пусть в точке М0(x0,y0) возможного
экстремума и в некоторой её
окрестности функция f(x,y) имеет
непрерывные частные производные
второго порядка и
f ( x0 , y0 ) f ( x0 , y0 ) [ f ( x0 , y0 )]
//
xx
f
f
//
xx
//
yx
//
yy
f
f
//
xy
//
yy
//
xy
2
14.
Тогда,1) если 0, то в точке М(x,y )функция
имеет экстремум и:
//
при f xx ( x0 , y0 ) 0 - максимум,
//
при f xx ( x0 , y0 ) 0 - минимум;
2) если 0 , то экстремума нет;
3) если 0 , то экстремум может
быть, а может и не быть.
15.
1516.
1617.
1718.
1819.
1920.
4. База получает некоторую продукцию с трёхзаводов 15%, 45%,40% соответственно. В
продукции первого завода брак составляет
4%, второго-6%, третьего-8%. Найти
вероятность того, что потребитель получит с
базы стандартное изделие.
n
P( A) P( H i ) P( A H i )
i 1
20
21.
2122.
5. В партии 55% изделий второго сорта,остальные первого сорта. Наудачу отобраны
2 изделия. Написать закон распределения.
Написать закон распределения случайной
величины Х – числа изделий второго сорта
среди отобранных. Найти числовые
характеристики (математическое ожидание
M(X), дисперсиюD(X), среднеквадратическое
отклонение).
22
23.
2324.
2425.
Вычисление определённого интеграла методом подстановки3
6 xdx
6. 2
3
(
x
1
)
2




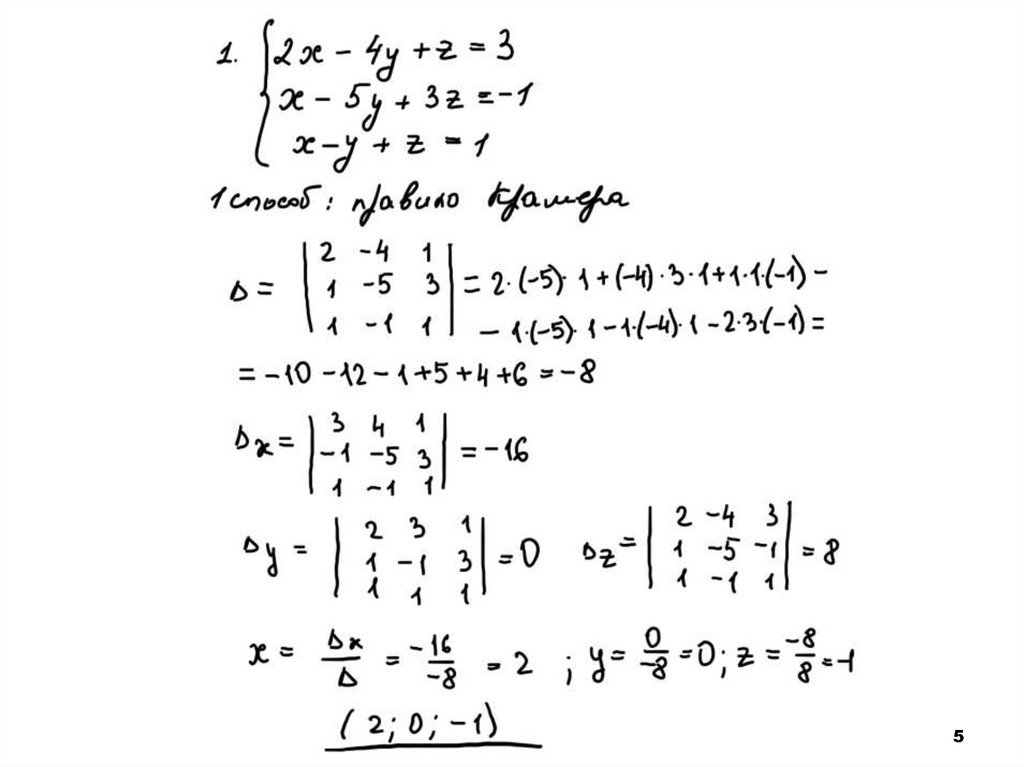


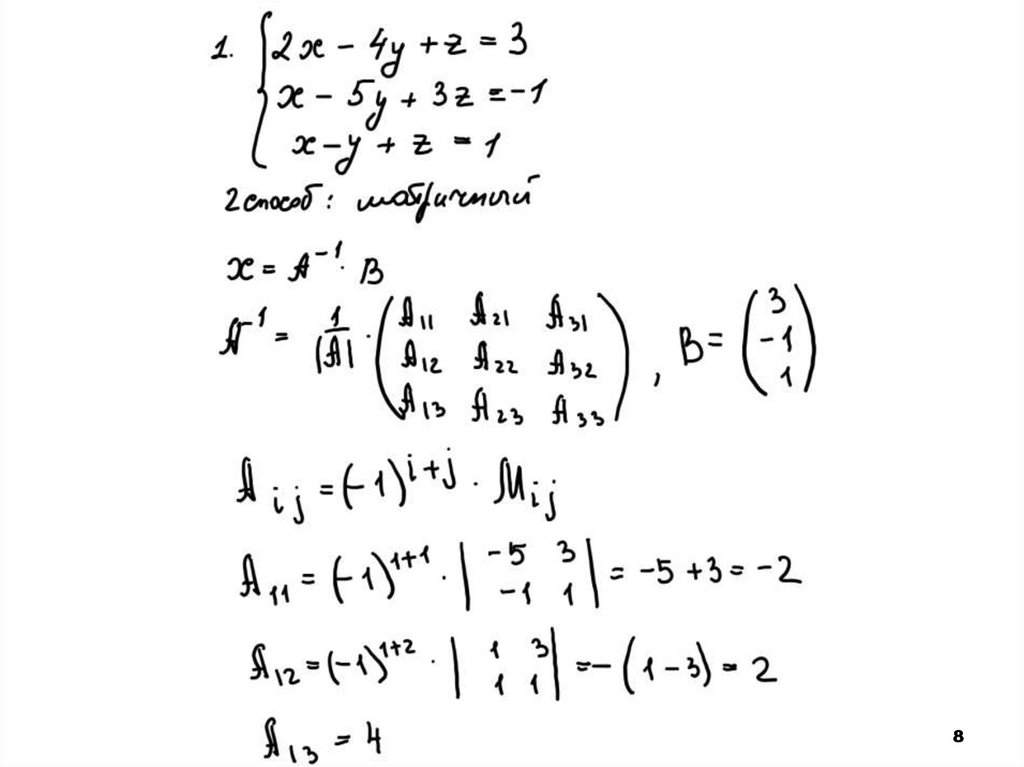
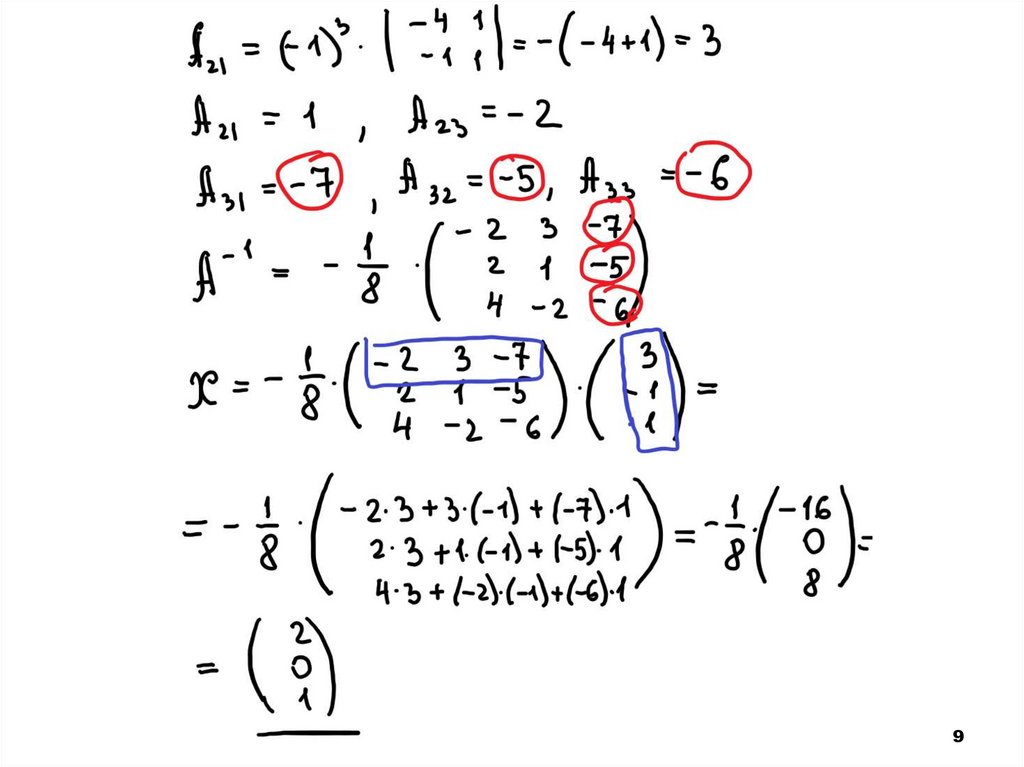
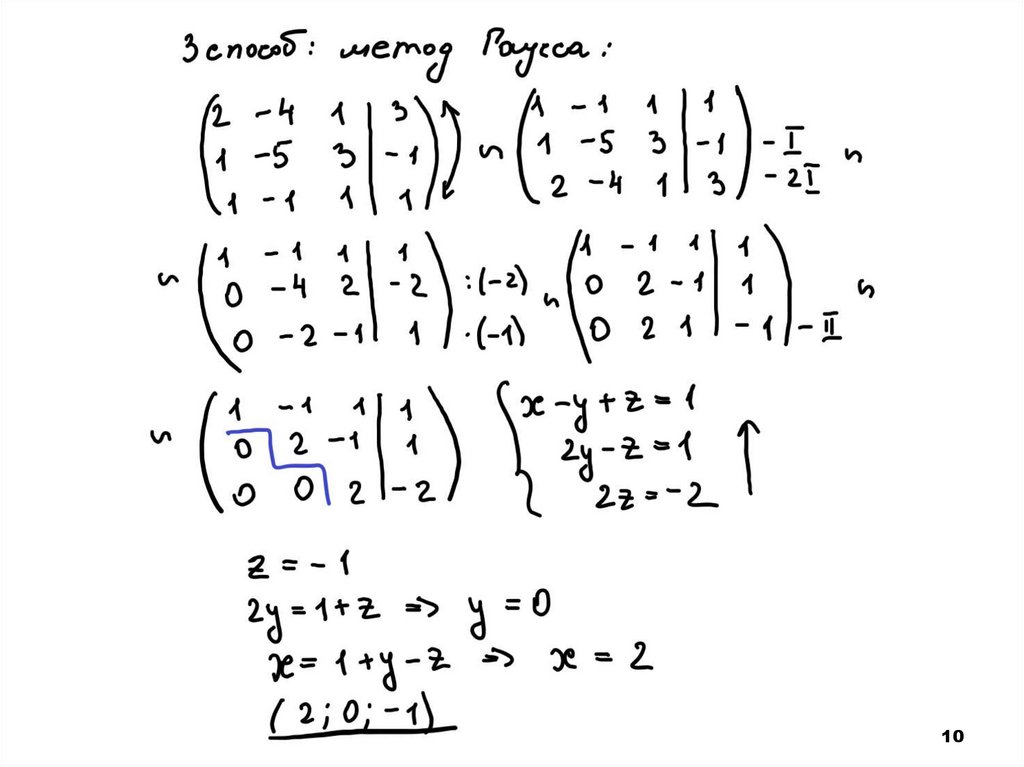




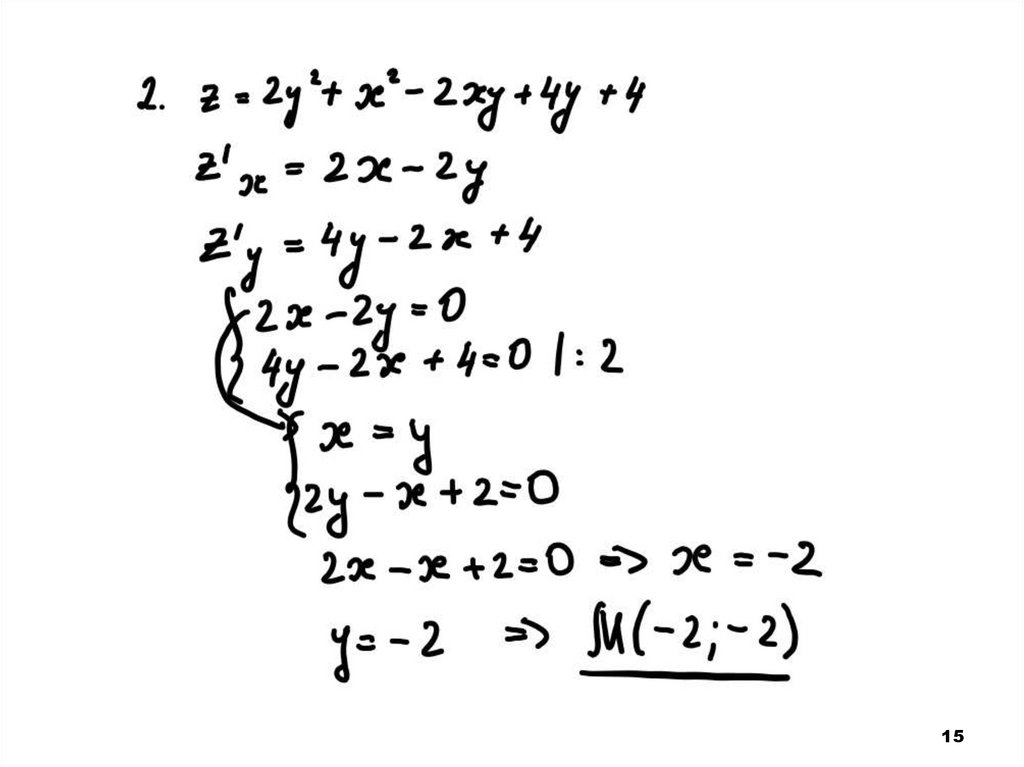
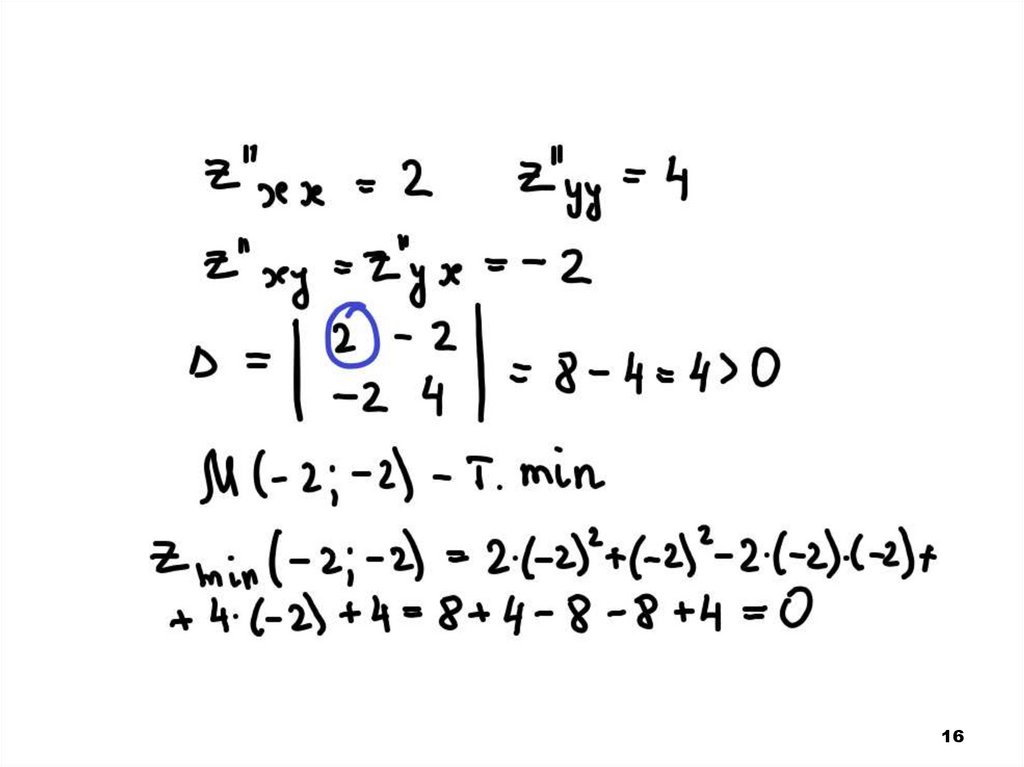

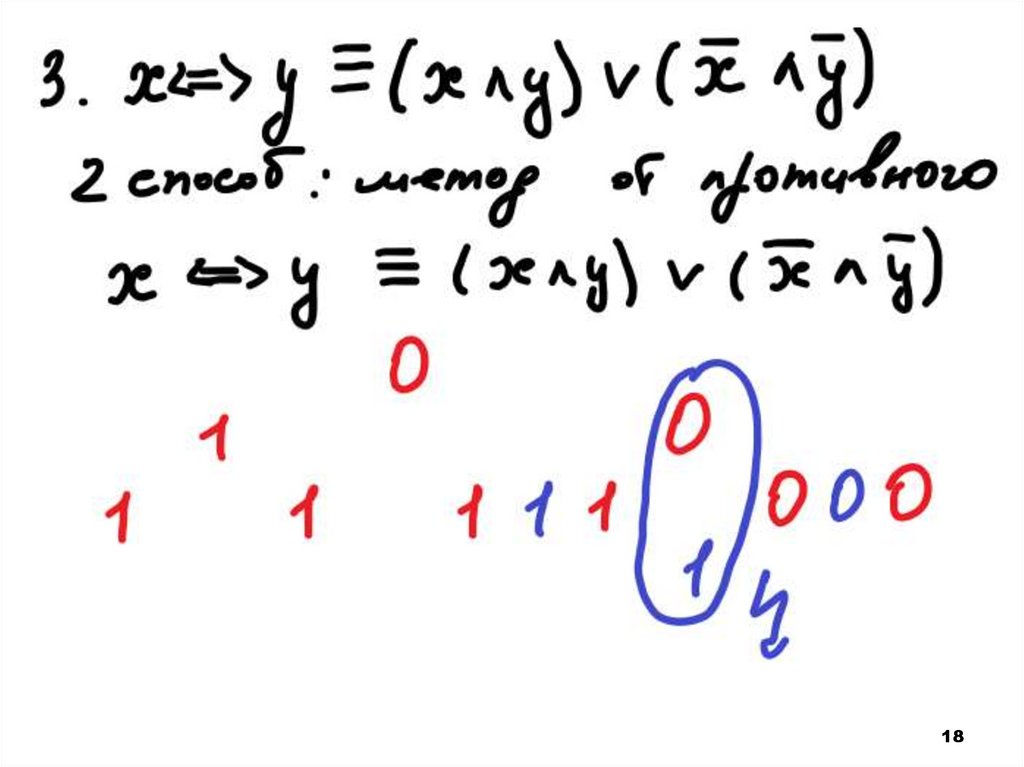
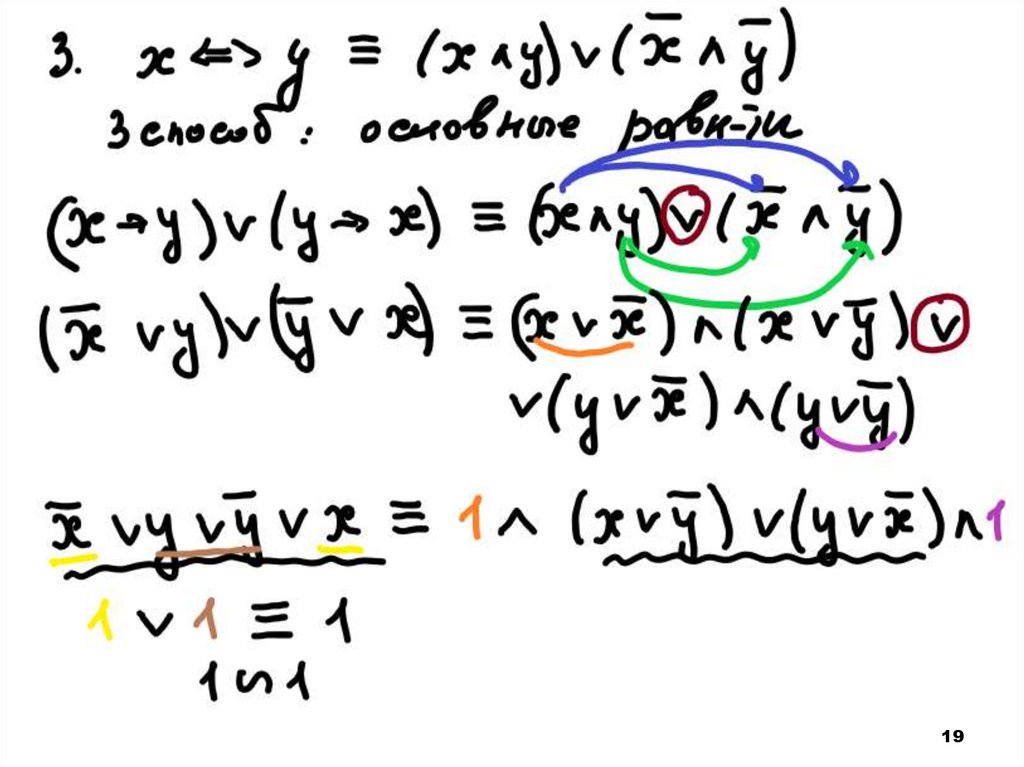



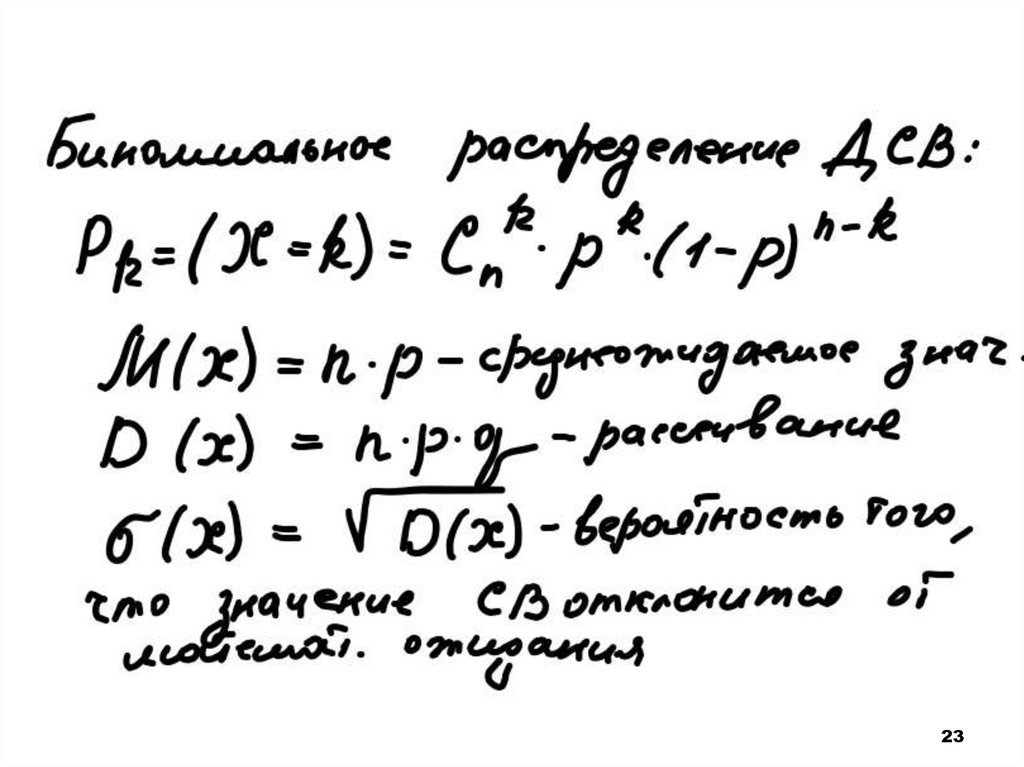
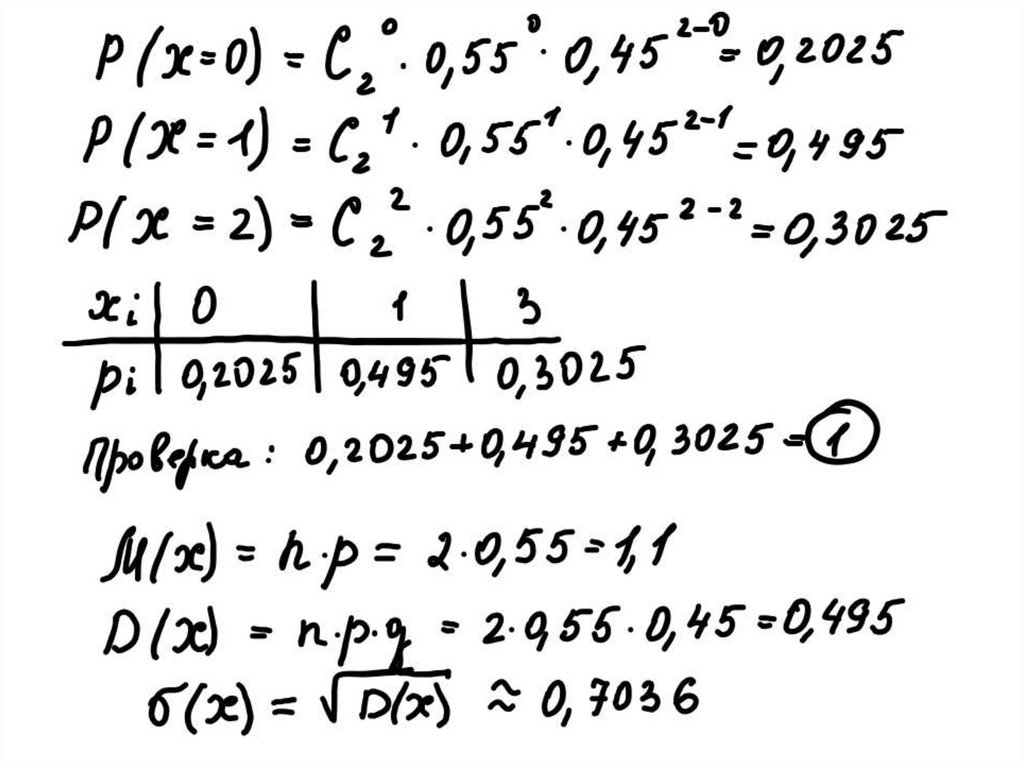



 Математика
Математика








