Физика ФЭН 2022

1. ФИЗИКА ФЭН 2022

2.

Сарина Марина Павловна
Доцент кафедры Прикладной и
теоретической физики, IV -210

3.

• Иродов И.Е. Основные законы
механики
• Трофимова Т.И. Курс физики
• Cарина.М.П. Механика, молекулярная
физика , термодинамика. Часть 1.
Механика, 2014
• Механика и термодинамика. Дубровский
В.Г, Корнилович А.А., Суханов И.И.
(Лабораторный практикум), 2019

4. Есть в библиотеке и в электронной библиотечной системе НГТУ (ЭБС)

5. Лабораторный практикум

6.

7.

8.

9.

• Курс на dispace № 12724
• ФЭН 2022 физика
• Физика механика № 4420
• Физика введение № 7821

10. ЭЛЕМЕНТЫ КИНЕМАТИКИ

11. Система отсчета

r ( x, y, z ) xi yj zk
Y
y
r
k
z
Z
j
A
x
O
i
X
r
- радиус -вектор

12.

• Система отсчета – это система
координат, указывающая
положение тела в пространстве, +
часы, необходимые для отсчета
времени
• В классической механике время
течет одинаково во всех системах
отсчета

13.

• Мы будем пользоваться декартовой
системой координат

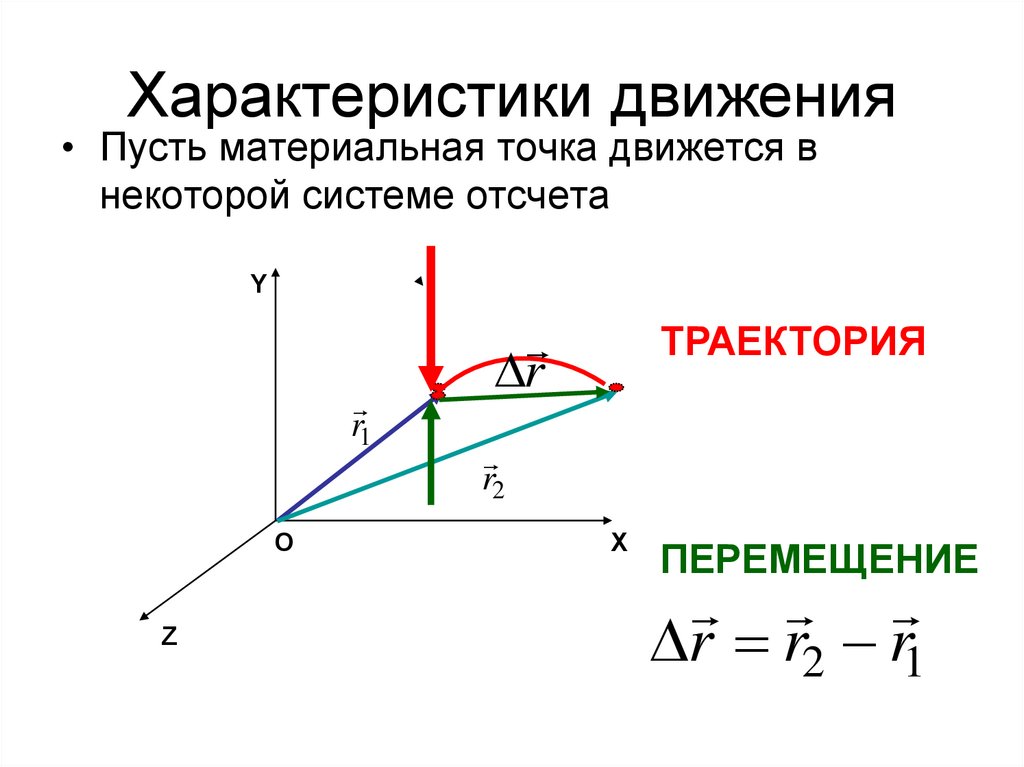
14. Характеристики движения

• Пусть материальная точка движется в
некоторой системе отсчета
Y
r1
O
Z
r
ТРАЕКТОРИЯ
r2
X
ПЕРЕМЕЩЕНИЕ
r r2 r1

15.

• Траектория – это линия, вдоль которой
материальная точка движется в
пространстве
• Вектор перемещения проводится из
начальной точки движения в конечную
• Путь – это длина траектории
(скалярная величина)

16. Мгновенная скорость

r
V lim
t 0 t
dr
V
dt

17.

Мгновенная скорость направлена
по касательной к траектории движения
в каждой точке
V1
r1
r2
V2
О
Скорость меняется по величине и
направлению

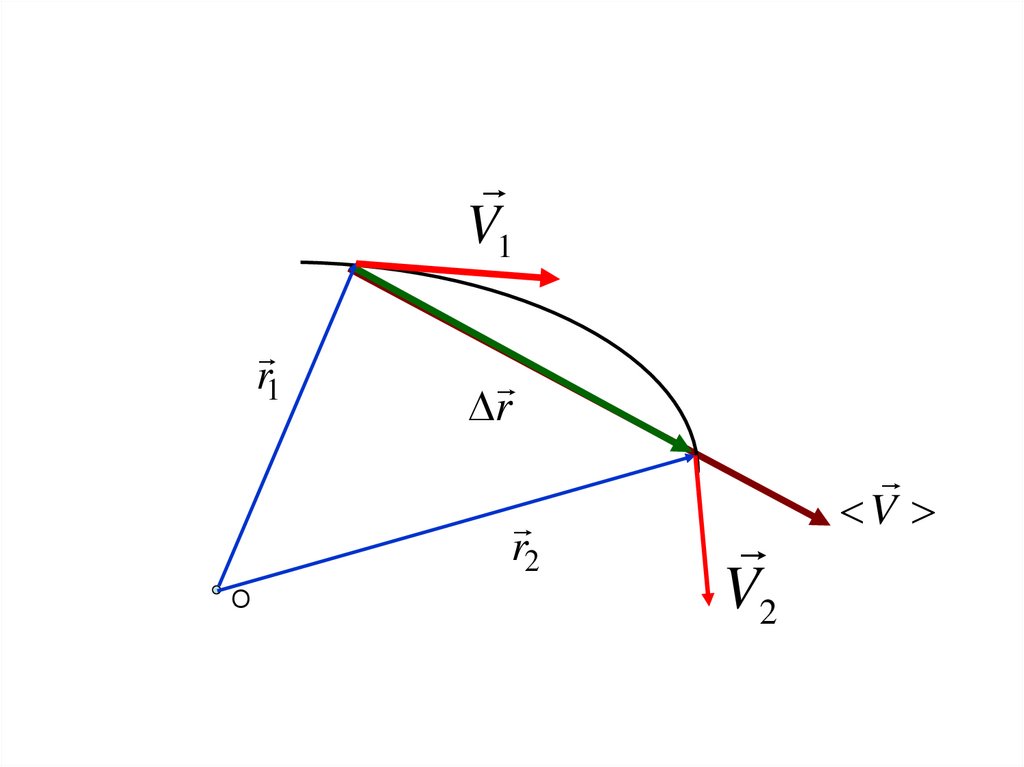
18. Средняя скорость

r
V
t
Средняя скорость –
отношение перемещения ∆r за время ∆t
к промежутку времени ∆t .
Направлена так же, как
вектор перемещения

19.

V1
r1
r
r2
О
V2
V

20. Ускорение

• Ускорение-быстрота изменения
скорости по модулю и направлению

21. Мгновенное ускорение

V
a lim
t 0 t
dV
a
dt
Мгновенное ускорение –
первая производная скорости
по времени.
2
d r
dr
d dr
a
2
V
a
dt
dt
dt dt

22. Среднее ускорение

V
a
t
V1
r1
V1
r2
О
a
V
V2

23. Координатный способ описания движения

r ( x, y, z ) xi yj zk
Y
y
r
k
z
Z
j
A
2
2
2
r x y z
x
O
i
X

24.

r ( x, y, z, t ) x(t )i y (t ) j z (t )k
dr ( x, y, z , t ) dx(t ) dy (t ) dz (t )
i
j
k
dt
dt
dt
dt
dr ( x, y, z , t )
V
dt
dx(t )
VX
dt
dy (t )
VY
dt
dz (t )
VZ
dt

25.

V VX i VY j VZ k
2
2
2
V VX VY VZ
аналогично для ускорения
a a X i aY j aZ k
2
2
2
a a X aY aZ

26. Криволинейное движение

27.

• В некоторых случаях не удобно
раскладывать ускорение на
координатные составляющие
• Естественный метод ( удобно
применять, когда известна траектория)

28.

V
V V
n
n
n
n 1
- Тангенциальная составляющая, направлена по касательной
-Нормальная составляющая,
направлена перпендикулярно касательной

29.

V V
dV d V
d
V
dt
dt
dt
dV
a
dt
d
a a V
dt
- Тангенциальное
ускорение
Определяет быстроту изменения скорости
по величине

30.

d
• Направление вектора
?
dt
• единичный вектор 1
• Скалярное произведение
1
• Продифференцируем
d
d d
dt
dt dt
d
2
0
dt

31.

• Вектора перпендикулярны
d
dt
d
dt
направлен по направлению
нормали n
• Второе слагаемое в формуле ускорения
d
V
an n
dt

32.

V1
V2
s
V
V2
R
R
V1 V2 V
V s
V
R

33.

• При малых углах
ds Vdt
Vdt
dV ds
R
V
R
2
dV Vdt
dV V a
n
R
V
dt
R

34.

d
V
an n
dt
an
V
2
- Нормальное
ускорение
Определяет быстроту изменения скорости
по направлению
- радиус кривизны траектории

35.

a a an
a
an
dV
a
dt
a
2
V
an
n
2
2
a a an

36. ПРИМЕР

an
R
R
a
dV
a
dt
a
2
V
an
R
- радиус окружности
если
V const
a 0
2
V
a an
R

37. Закон сложения скоростей

38.

t
Y
y
Y´
y´
t
r
r0
z
Z
r
A
x´
X´
z´
Z´
x
r r0 r t t
X

39.

• Пусть система отсчета К´ движется
относительно системы отсчета К со
скоростью V0
• Системы отсчета движущаяся
равномерно и прямолинейно, либо
находящаяся в состоянии покоя
называется инерциальной

40.

r0 V0t
r r0 r
V0t r

41.

• В проекциях на оси координат
x x V0 xt
y y V0 yt
z z V0 z t
• V0x, V0y,, V0z – проекции скорости на оси
координат

42. Закон сложения скоростей

r r0 r
dr dr0 dr
dt dt dt
V V0 V

43.

• Скорость движения
точки относительно
системы отсчета К
• Скорость движения
точки относительно
системы отсчета К´
• Скорость движения
системы отсчета К´
относительно
системы отсчета К
V
dr
V
dt
V
dr
V
dt
V0
dr0
V0
dt

44.

V V0 V
Y
V
Y´
V0
Z´
Z
V
X´
V
V0
X

45. Пример

река
течение
лодка
r
r0
r
плот
r r0 r
V V0 V

46. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ

47.

V0 y V0 z 0
Y
t
t
Y´
r
A
X´
Z´
Z
V0
X

48.

x x V0t
y y
z z
t t

49.

V V0 V
dV dV0 dV
dt
dt
dt
dV
a
dt
dV
a
dt
a a
V0 const
t t
dV0
0
dt

50. Принцип относительности Галилея

• Все законы механики имеют
одинаковую форму во всех
инерциальных системах отсчета