Похожие презентации:
Кинематика материальной точки
1. Кинематика материальной точки
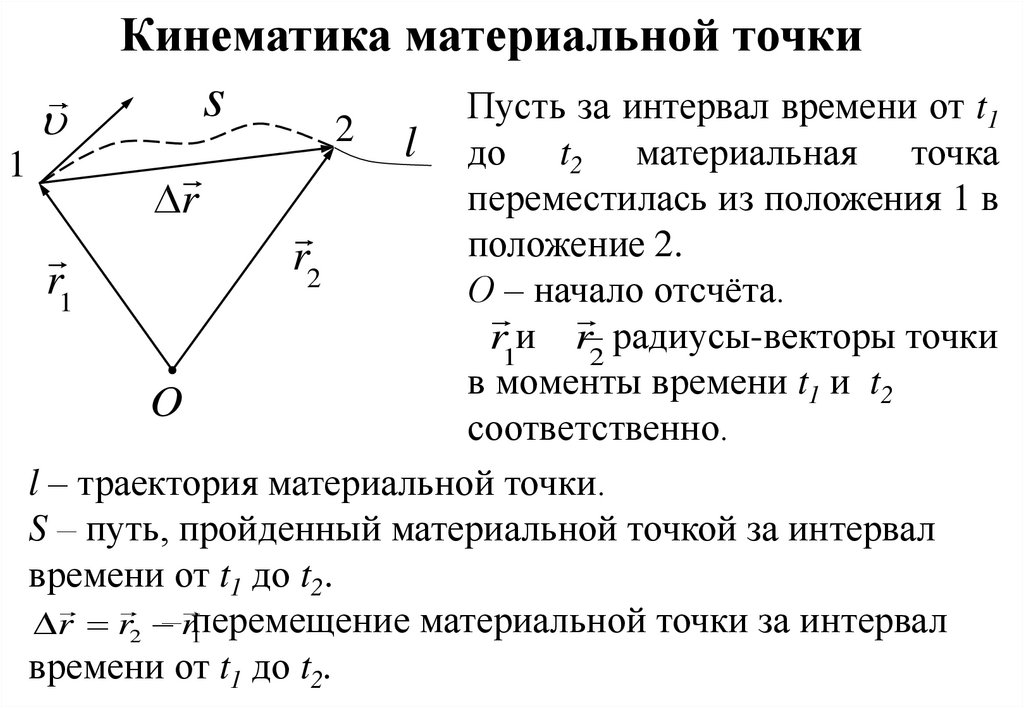
sПусть за интервал времени от t1
2 l
до t2 материальная точка
1
переместилась из положения 1 в
r
положение 2.
r2
r1
О – начало отсчёта.
r1и r–2 радиусы-векторы точки
в моменты времени t1 и t2
O
соответственно.
l – траектория материальной точки.
S – путь, пройденный материальной точкой за интервал
времени от t1 до t2.
r r2 –r1перемещение материальной точки за интервал
времени от t1 до t2.
2. Линейная скорость материальной точки.
v1Линейная скорость материальной точки.
r
r1
O
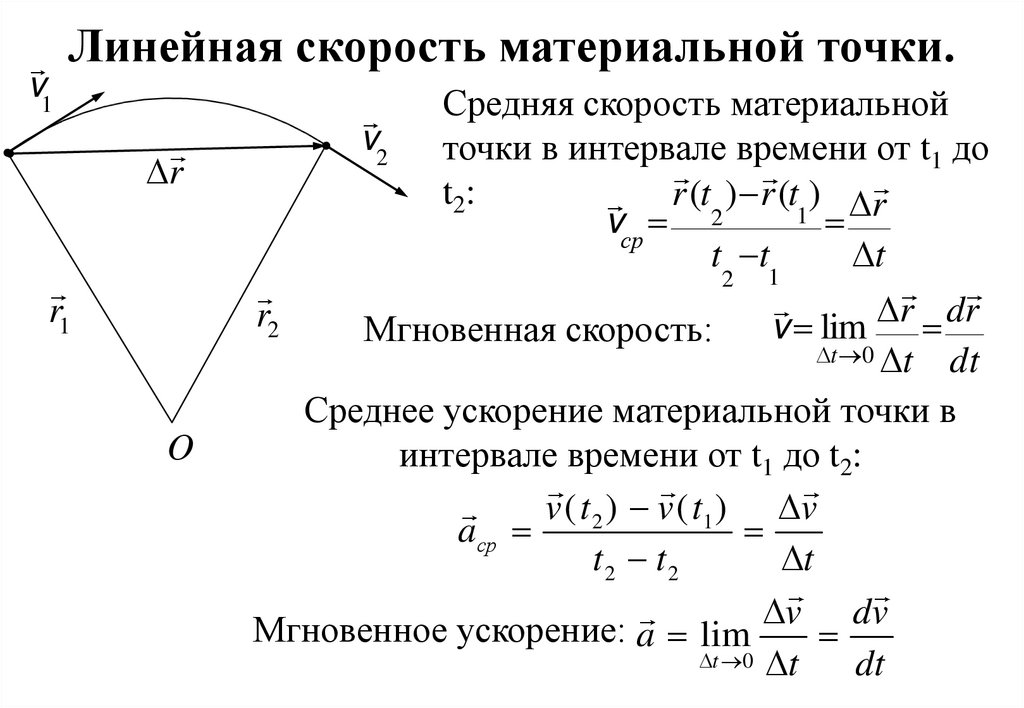
Средняя скорость материальной
точки в интервале времени от t1 до
t2:
r (t2 ) r (t1) r
vср
t t
t
2 1
r dr
r2
v
lim
Мгновенная скорость:
t 0 t
dt
Среднее ускорение материальной точки в
интервале времени от t1 до t2:
v ( t 2 ) v ( t1 ) v
aср
t2 t2
t
v dv
Мгновенное ускорение: a lim
t 0 t
dt
v2
3. Средняя скорость прохождения отрезка пути.
vср St
Средний путевой скоростью движения точки называется
скалярная величина равная отношению пути, пройденного
точкой за интервал времени t к его продолжительности.
Пример:
A
vср
v2
v1
S
B
2S
S
v
1
S
v2
v1 v 2
v1 v 2
4. Векторный способ описания движения
r r (t )dr
v
dt
2
dv
d
r
Ускорение материальной точки:
a
dt
dt
Скорость материальной точки в момент времени t:
Скорость материальной точки:
t
v ( t ) v0 a ( t ) dt ,
0
где 0– скорость материальной точки в момент времени t=0.
Радиус-вектор материальной точки в момент времени t:
t
r ( t ) r0 v ( t ) dt
0
Перемещение материальной точки за интервал времени
t
от 0 до t:
r v ( t ) dt
0
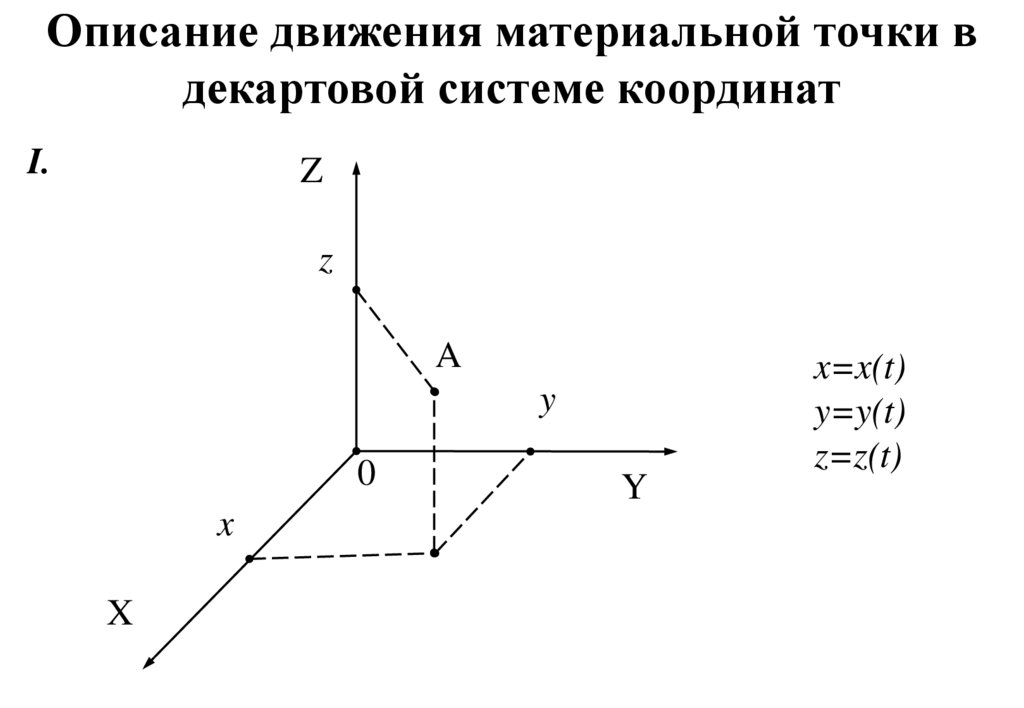
5. Описание движения материальной точки в декартовой системе координат
I.Z
z
A
y
0
x
X
Y
x=x(t)
y=y(t)
z=z(t)
6. II. Скорость материальной точки
Проекции вектора скорости на оси координат:dx
dy
dz
vx
; vy
; vz
dt
dt
dt
v v x2 v y2 v z2
Модуль вектора скорости:
Косинусы углов, которые вектор скорости
составляет с осями Ox, Oy, Oz:
vx
Cos ;
v
Cos
vy
v
;
vz
Cos
v
7. III. Ускорение материальной точки
Проекция вектора ускорения на оси координат:dv x d 2 x
ax
2;
dt
dt
d 2y
ay
2;
dt
dt
dv y
Модуль вектора ускорения:
dv z d 2 z
az
2
dt
dt
a a x2 a y2 a z2
Косинусы углов, которые вектор ускорения
составляет с осями Ox, Oy, Oz:
ay
a
x
Cos ; Cos ; Cos a z
a
a
a
8. IV. Перемещение материальной точки за интервал времени от t1 до t2
Проекция вектора перемещения на оси координат:rx x2 x1
ry y2 y1
rz z2 z1
Модуль вектора перемещения:
r rx2 ry2 rz2
Косинусы углов, которые вектор перемещения
составляет с осями Ox, Oy, Oz:
ry
r
x
Cos ; Cos ; Cos r z
r
r
r
9. Траекторный способ описания движения
Дуговая координата: l=l(t)Скорость материальной точки:
l
n
dl
v
v
dt
Полное ускорение материальной точки:
O
v
dv
v d d v
1
2
a
v
n
dt
dt
dt
R кр
v0
a
an
a
an
a a 2 an2
Если v , a v
Если v , a v
g
an
a
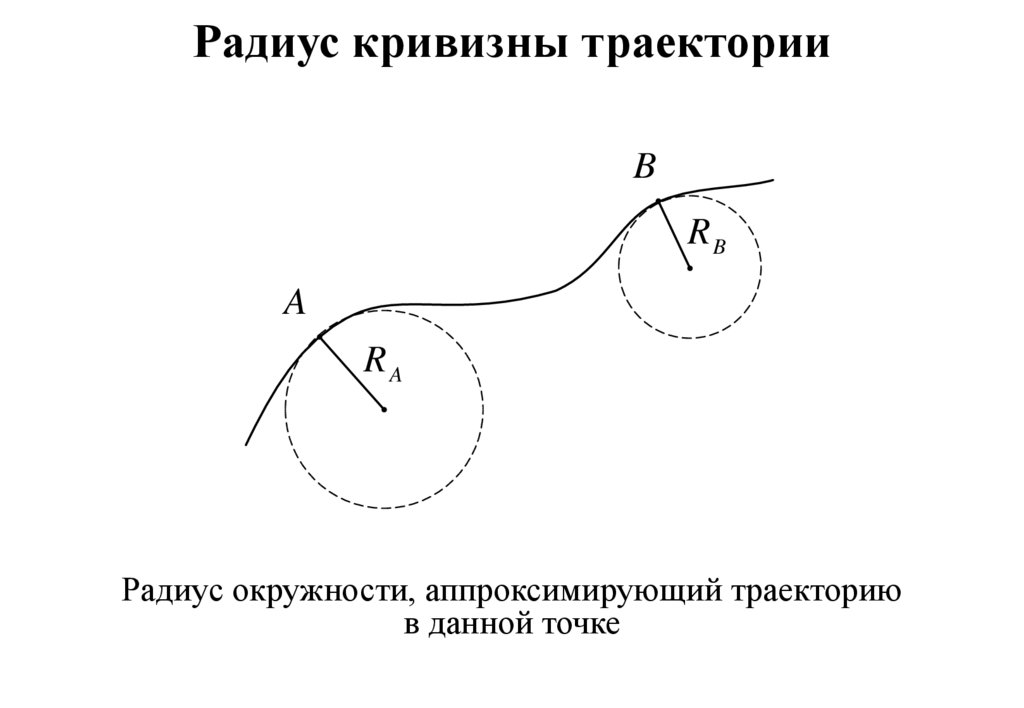
10. Радиус кривизны траектории
BRB
A
RA
Радиус окружности, аппроксимирующий траекторию
в данной точке
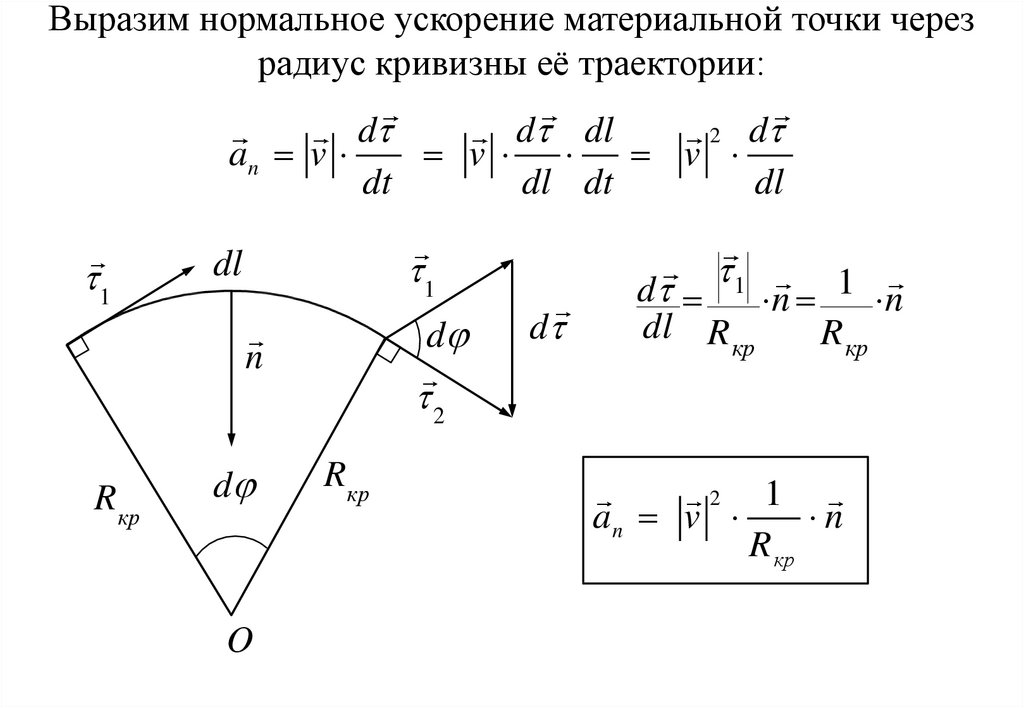
11. Выразим нормальное ускорение материальной точки через радиус кривизны её траектории:
dd dl
2 d
an v
v
v
dt
dl dt
dl
1
1
dl
d
2
n
Rкр
d
O
Rкр
d
1
1
d
n
n
dl R кр
R кр
1
an v
n
R кр
2
12. Движение с постоянным ускорением .
Движение с постоянным ускорением a const.
Зависимость скорости материальной точки от времени:
v ( t ) v0 a t
v0 - скорость материальной точки в момент времени t=0.
Зависимость радиуса-вектора материальной точки от
времени:
at 2
r ( t ) r0 v0t
2
r0 - радиус-вектор материальной точки в момент времени
t=0.
Перемещение материальной точки за интервал
времени от 0 до t:2
at
r ( t ) v0t
2
13. Движение с постоянным ускорением Формула для разности квадратов скоростей
v0O
x0
a
v
x
X
ax t 2
x x 0 v0 x t
v x v0 x a x t
2
Приращение координаты материальной точки за интервал
времени от 0 до t:
v x2 v02x
x x x 0
2a x
Проекция на ось Ох перемещения материальной точки за
2
2
интервал времени от 0 до t:
v x v0 x
r x x
2a x
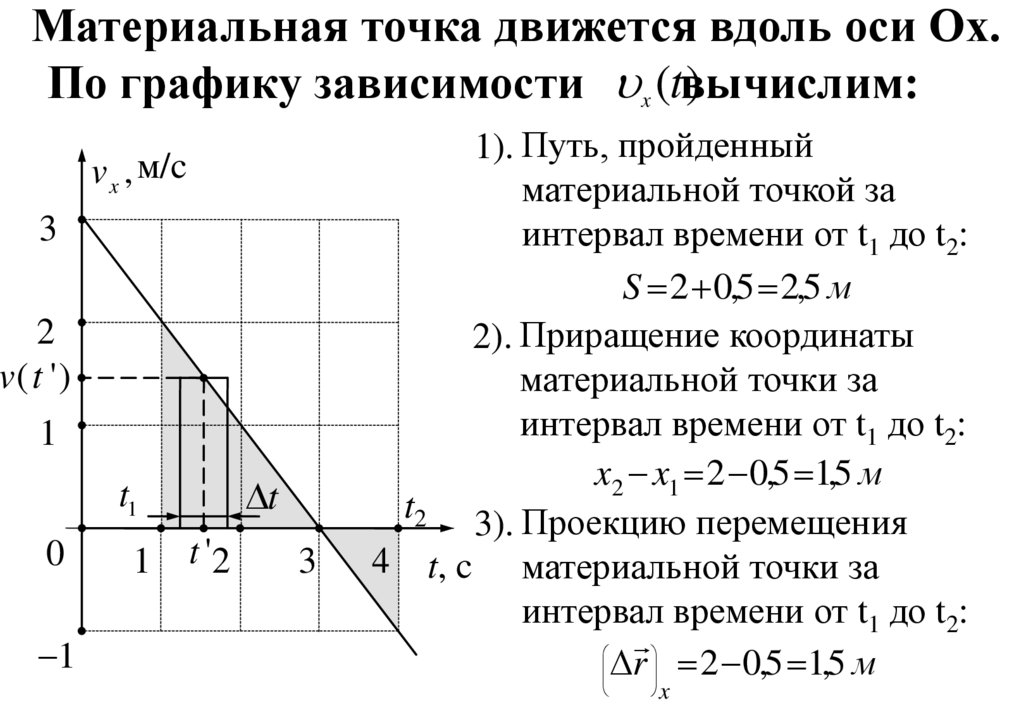
14. Материальная точка движется вдоль оси Ох.
)По графику зависимости x (tвычислим:
v x , м/c
3
2
v ( t ')
1
t
t1
0
1
1
t '2
3
1). Путь, пройденный
материальной точкой за
интервал времени от t1 до t2:
S 2 0,5 2,5 м
2). Приращение координаты
материальной точки за
интервал времени от t1 до t2:
x2 x1 2 0,5 1,5 м
t2 3). Проекцию перемещения
4 t, c материальной точки за
интервал времени от t1 до t2:
r 2 0,5 1,5 м
x
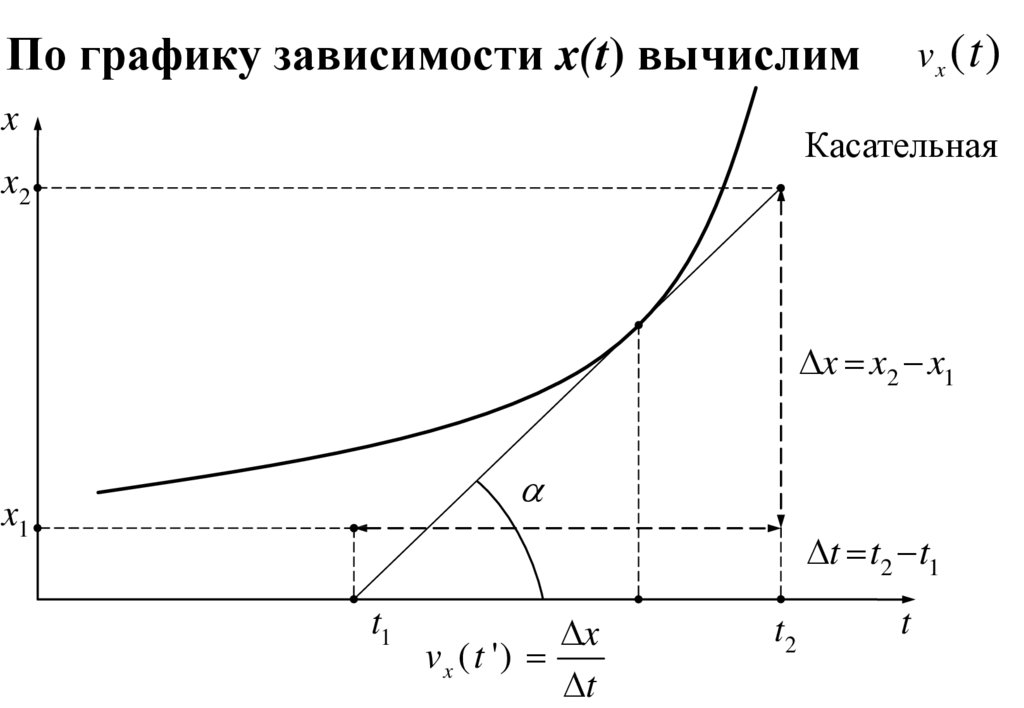
15. По графику зависимости x(t) вычислим
xvx ( t )
Касательная
x2
x x2 x1
x1
t t2 t1
t1
x
v x ( t ')
t
t2
t
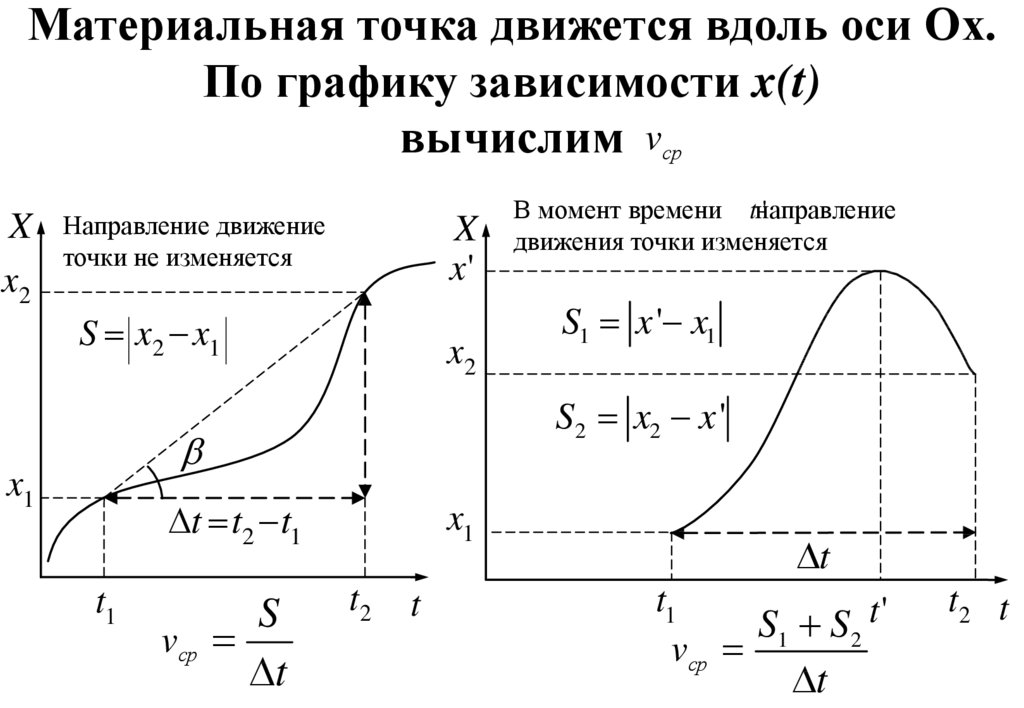
16.
Материальная точка движется вдоль оси Ох.По графику зависимости x(t)
вычислим vср
X
x2
Направление движение
точки не изменяется
X
x'
S x2 x1
x2
t t2 t1
t1
S
vср
t
S1 x ' x1
S2 x2 x '
x1
'
В момент времени tнаправление
движения точки изменяется
x1
t2
t
t
t1
S1 S2 t '
vср
t
t2 t
17. Кинематика равномерного вращения материальной точки по окружности
2 RПериод обращения точки:
T
Частота обращения точки:
1
T
Центростремительное ускорение:
R
aцс
v лин
2
[T ] c
c 1
2
v
aцс 2R
R
18. Кинематика вращения твёрдого тела вокруг неподвижной оси.
dУгол поворота:
d
Угловая скорость:
d
рад
с
dt
Угловое ускорение:
d d 2
рад
r
с2
dt dt 2
O
Если: , , если: , .
2
(t ) 0 t ,
( t ) 0 t t
Если const ,
2 18
19. Кинематика вращения твёрдого тела вокруг неподвижной оси. Связь линейных и угловых величин.
Zd
d
dr
r
O
n
v
dr d , r
, r
dv d , r
a
dt
dt
, r
z
a
:dt
dr
,
dt
, , r
2
n
an
Л2
19
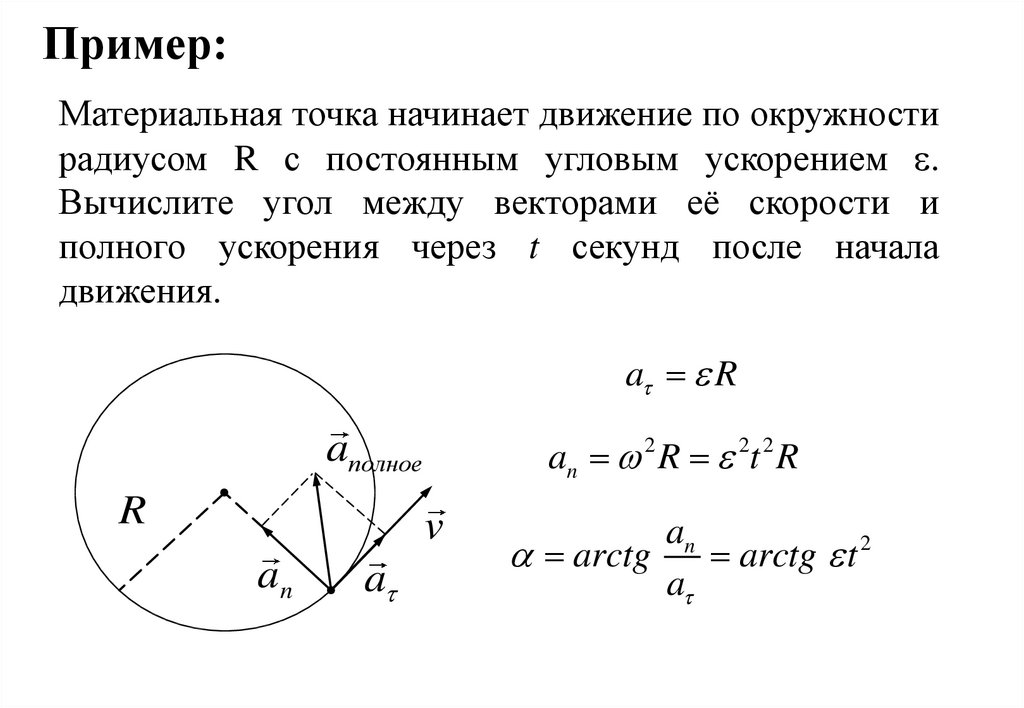
20. Пример:
Материальная точка начинает движение по окружностирадиусом R с постоянным угловым ускорением .
Вычислите угол между векторами её скорости и
полного ускорения через t секунд после начала
движения.
a R
an 2 R 2t 2 R
aполное
R
v
an
a
an
arctg
arctg t 2
a
21. Равноускоренное движение материальной точки по окружности.
Зависимость угловойскорости от времени:
0 t
z
Зависимость приращения
угла поворота от времени:
0t
z 0z z t
t
2
2
z 0 z t
z t2
2












 Физика
Физика








